An Eulerian approach to transport and diffusion on evolving implicit surfaces

Abstract

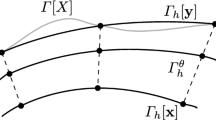
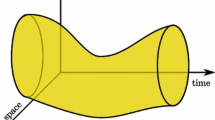
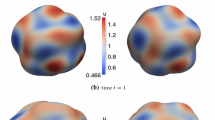
In this article we define a level set method for a scalar conservation law with a diffusive flux on an evolving hypersurface Γ(t) contained in a domain ${\Omega \subset \mathbb R^{n+1}}$ . The partial differential equation is solved on all level set surfaces of a prescribed time dependent function Φ whose zero level set is Γ(t). The key idea lies in formulating an appropriate weak form of the conservation law with respect to time and space. A major advantage of this approach is that it avoids the numerical evaluation of curvature. The resulting equation is then solved in one dimension higher but can be solved on a fixed grid. In particular we formulate an Eulerian transport and diffusion equation on evolving implicit surfaces. Using Eulerian surface gradients to define weak forms of elliptic operators naturally generates weak formulations of elliptic and parabolic equations. The finite element method is applied to the weak form of the conservation equation yielding an Eulerian Evolving Surface Finite Element Method. The computation of the mass and element stiffness matrices, depending only on the gradient of the level set function, are simple and straightforward. Numerical experiments are described which indicate the power of the method. We describe how this framework may be employed in applications.