Abstract
The large majority of risk-sharing transactions involve few agents, each of whom can heavily influence the structure and the prices of securities. In this paper, we propose a game where agents’ strategic sets consist of all possible sharing securities and pricing kernels that are consistent with Arrow–Debreu sharing rules. First, it is shown that agents’ best response problems have unique solutions. The risk-sharing Nash equilibrium admits a finite-dimensional characterisation, and it is proved to exist for an arbitrary number of agents and to be unique in the two-agent game. In equilibrium, agents declare beliefs on future random outcomes different from their actual probability assessments, and the risk-sharing securities are endogenously bounded, implying (among other things) loss of efficiency. In addition, an analysis regarding extremely risk-tolerant agents indicates that they profit more from the Nash risk-sharing equilibrium than compared to the Arrow–Debreu one.
Similar content being viewed by others
1 Introduction
The structure of securities that optimally allocate risky positions under heterogeneous beliefs of agents has been a subject of ongoing research. Starting from the seminal works of [10, 5, 13, 12], the existence and characterisation of welfare risk sharing of random positions in a variety of models has been extensively studied—see, among others, [7, 19, 1, 16]. On the other hand, discrepancies amongst agents regarding their assessments on the probability of future random outcomes reinforce the existence of mutually beneficial trading opportunities (see e.g. [28, 29, 8]). However, market imperfections, such as asymmetric information, transaction costs and oligopolies, spur agents to act strategically and prevent markets from reaching maximum efficiency. In the financial risk-sharing literature, the impact of asymmetric or private information has been addressed under both static and dynamic models (see, among others, [6, 21, 22, 23, 31]). The importance of frictions like transaction costs has been highlighted in [3]; see also [14].
The present work aims to contribute to the risk-sharing literature by focusing on how over-the-counter (OTC) transactions with a small number of agents motivate strategic behaviour. The vast majority of real-world sharing instances involve only a few participants, each of whom may influence the way heterogeneous risks and beliefs are going to be allocated. (The seminal papers [20] and [30] highlight such transactions.) As an example, two financial institutions with possibly different beliefs, and in possession of portfolios with random future payoffs, may negotiate and design innovative asset-backed securities that mutually share their defaultable assets. Broader discussion on risk-sharing innovative securities is given in the classical reference [4] and in [27]; a list of widely used such securities is provided in [17].
As has been extensively pointed out in the literature (see e.g. [29] and [26]), it is reasonable, and perhaps even necessary, to assume that agents have heterogeneous beliefs, which we identify with subjective probability measures on the considered state space. In fact, differences in subjective beliefs do not necessarily stem from asymmetric information; agents usually apply different tools or models for the analysis and interpretation of common sets of information.
Formally, a risk-sharing transaction consists of security payoffs and their prices, and since only few institutions (typically, two) are involved, it is natural to assume that no social planner for the transaction exists and that the equilibrium valuation and payoffs will result as the outcome of a symmetric game played among the participating institutions. Since institutions’ portfolios are (at least approximately) known, the main ingredient of risk-sharing transactions leaving room for strategic behaviour is the beliefs that each institution reports for the sharing. We propose a novel way of modelling such strategic actions where the agents’ strategic set consists of the beliefs that each one chooses to declare (as opposed to their actual one) aiming to maximise individual utility, and the induced game leads to an equilibrium sharing. Our main insights are summarised below.
1.1 Main contributions
The payoff and valuation of the risk-sharing securities are endogenously derived as an outcome of agents’ strategic behaviour under constant absolute risk-aversion (CARA) preferences. To the best of our knowledge, this work is the first instance that models the way agents choose the beliefs on future uncertain events that they are going to declare to their counterparties and studies whether such strategic behaviour results in equilibrium. Our results demonstrate how the game leads to risk-sharing inefficiency and security mispricing, both of which are quantitatively characterised in analytic forms. More importantly, it is shown that equilibrium securities have endogenous limited liability, a feature that, while usually suboptimal, is in fact observed in practice.
Although the agents’ set of strategic choices is infinite-dimensional, one of our main contributions is to show that a Nash equilibrium admits a finite-dimensional characterisation with the dimensionality being one less than the number of participating agents. Not only does our characterisation provide a concrete algorithm for calculating the equilibrium transaction, it also allows us to prove the existence of Nash equilibrium for an arbitrary number of players. In the important case of two participating agents, we even show that a Nash equilibrium is unique. It has to be pointed out that the aforementioned results are obtained under complete generality on the probability space and the involved random payoffs—no extra assumption except from CARA preferences is imposed. Whereas a certain qualitative analysis could be potentially carried out without the latter assumption on the entropic form of agent utilities, the advantage of CARA preferences utilised in the present paper is that they also allow a substantial quantitative analysis, as workable expressions are obtained for Nash equilibrium.
Our notion of Nash risk-sharing equilibrium highlights the importance of agents’ risk-tolerance level. More precisely, one of the main findings of this work is that agents with sufficiently low risk-aversion will prefer the risk-sharing game rather than the outcome of an Arrow–Debreu equilibrium that would have resulted from absence of strategic behaviour. Interestingly, the result is valid irrespective of their actual risky position or their subjective beliefs. It follows that even risk-averse agents, as long as their risk-aversion is sufficiently low, will prefer risk-sharing markets that are thin (i.e., where participating agents are few and have the power to influence the transaction), resulting in aggregate loss of risk-sharing welfare.
1.2 Discussion
Our model is introduced in Sect. 2 and consists of a two-period financial economy with uncertainty, containing possibly infinitely many states of the world. Such infinite-dimensionality is essential in our framework since in general the risks that agents encounter do not have a priori bounds, and we do not wish to enforce any restrictive assumption on the shape of the probability distribution or the support of agents’ positions. Let us also note that even if the analysis was carried out in the simpler setup of a finite state space, there would not be any significant simplification in the mathematical treatment.
In our economy, we consider a finite number of agents, each of whom has subjective beliefs (probability measure) about the events at the time of uncertainty resolution. We also allow agents to be endowed with a (cumulative, up to the point of uncertainty resolution) random endowment.
Agents seek to increase their expected utilities through trading securities that allocate the discrepancies of their beliefs and risky exposures in an optimal way. The possible disagreement on agents’ beliefs is assumed on the whole probability space, and not only on the laws of the to-be-shared risky positions. Such potential disagreement is important: it alone can give rise to mutually beneficial trading opportunities, even if agents have no risky endowments to share, by actually designing securities with payoffs written on the events where probability assessments are different.
Each sharing rule consists of the security payoff that each agent is going to obtain and a valuation measure under which all imaginable securities are priced. The sharing rules that efficiently allocate any submitted discrepancy of beliefs and risky exposures are the ones stemming from an Arrow–Debreu equilibrium. (Under CARA preferences, the optimal sharing rules have been extensively studied; see e.g. [10, 13, 7].) In principle, participating agents would opt for the highest possible aggregate benefit from the risk-sharing transaction, as this would increase their chance for personal gain. However, in the absence of a social planner that could potentially impose a truth-telling mechanism, it is reasonable to assume that agents do not negotiate the rules that will allocate the submitted endowments and beliefs. In fact, we assume that agents adapt the specific sharing rules that are consistent with the ones resulting from an Arrow–Debreu equilibrium, treating reported beliefs as actual ones, since these sharing rules are the most natural and universally regarded as efficient.
Agreement on the structure of risk-sharing securities is also consistent with what is observed in many OTC transactions involving security design, where the contracts signed by institutions are standardised and adjusted according to required inputs (in this case, the agents’ reported beliefs). Such pre-agreement on sharing rules reduces negotiation time and hence also the related transaction costs. Examples are asset-backed securities, whose payoffs are backed by issuers’ random incomes, traded among banks and investors in a standardised form, as well as credit derivatives, where portfolios of defaultable assets are allocated among financial institutions and investors.
Combinations of strategic and competitive stages are widely used in the literature of financial innovation and risk-sharing under a variety of different guises. The majority of this literature distinguishes participants among designers (or issuers) of securities and investors who trade them. In [15], a security-design game is played among exchanges, each aiming to maximise internal transaction volume; while security design throughout exchanges is the outcome of non-competitive equilibrium, investors trade securities in a competitive manner. Similarly, in [9], a Nash equilibrium determines not only the designed securities among financial intermediaries, but also the bid-ask spread that price-taking investors have to face in the second (perfect competition) stage of market equilibrium. In [14], it is entrepreneurs who strategically design securities that investors with non-securitised hedging need competitively trade. In [24], the role of security-designers is played by arbitrageurs who issue innovated securities in segmented markets. A mixture of strategic and competitive stages has also been used in models with asymmetric information. For instance, in [11], a two-stage equilibrium game is used to model security design among agents with private information regarding their effort. In a first stage, agents strategically issue novel financial securities; in the second stage, equilibrium on the issued securities is formed competitively.
Our framework models oligopolistic OTC security design, where participants are not distinguished regarding their information or ability to influence market equilibrium. Agents mutually agree to apply Arrow–Debreu sharing rules since these optimally allocate whatever is submitted for sharing, and also strategically choose the inputs of the sharing rules (their beliefs, in particular).
Given the agreed-upon rules, agents propose accordingly consistent securities and valuation measures, aiming to maximise their own expected utility. As explicitly explained in the text, proposing risk-sharing securities and a valuation kernel is in fact equivalent to agents reporting beliefs to be considered for sharing. Knowledge of the probability assessments of the counterparties may result in a readjustment of the probability measure an agent is going to report for the transaction. In effect, agents form a game by responding to other agents’ submitted probability measures; the fixed point of this game (if it exists) is called a Nash risk-sharing equilibrium.
The first step of analysing Nash risk-sharing equilibria is to address the well-posedness of an agent’s best response problem, which is the purpose of Sect. 3. Agents have motive to exploit other agents’ reported beliefs and hedging needs and drive the sharing transaction to maximise their own utility. Each agent’s strategic choice set consists of all possible probability measures (equivalent to a baseline measure), and the optimal one is called the best probability response. Although this is a highly nontrivial infinite-dimensional maximisation problem, we use a bare-hands approach to establish that it admits a unique solution. It is shown that the beliefs that an agent declares coincide with the actual ones only in the special case where the agent’s position cannot be improved by any transaction with other agents. By resorting to examples, one may gain more intuition on how future risk appears under the lens of agents’ reported beliefs. Consider for instance two financial institutions adapting distinct models for estimating the likelihood of the involved risks. The sharing contract designed by the institutions will result from individual estimation of the joint distribution of the to-be-shared risky portfolios. According to the best probability response procedure, each institution tends to use a less favourable assessment for its own portfolio than the one based on its actual beliefs, and understates the downside risk of its counterparty’s portfolio. Example 3.8 contains an illustration of such a case.
An important consequence of applying the best probability response is that the corresponding security that the agent wishes to acquire has bounded liability. If only one agent applies the proposed strategic behaviour, then the received security payoff is bounded below (but not necessarily bounded above). In fact, the arguments and results of the best response problem receive extra attention and discussion in the paper since they demonstrate in particular the value of the proposed strategic behaviour in terms of utility increase. This situation applies to markets where one large institution trades with a number of small agents, each of whom has negligible market power.
A Nash-type game occurs when all agents apply the best probability response strategy. In Sect. 4, we characterise a Nash equilibrium as the solution of a certain finite-dimensional problem. Based on this characterisation, we establish the existence of a Nash risk-sharing equilibrium for an arbitrary (finite) number of agents. In the special case of two-agent games, the Nash equilibrium is shown to be unique. The finite-dimensional characterisation of Nash equilibria also provides an algorithm that can be used to approximate the Nash equilibrium transaction by standard numerical procedures, such as Monte Carlo simulation.
Having characterised Nash equilibria, we are able to further perform a joint qualitative and quantitative analysis. Not only do we verify the expected fact that in any nontrivial case, Nash risk-sharing securities are different from the Arrow–Debreu ones, but we also provide analytic formulas for their shapes. Since the securities that correspond to the best probability response are bounded from below, the application of such a strategy from all agents yields that the Nash risk-sharing market-clearing securities are also bounded from above. This comes in stark contrast to Arrow–Debreu equilibrium and implies in particular an important loss of efficiency. We measure the risk-sharing inefficiency that is caused by the game via the difference between the aggregate monetary utilities at Arrow–Debreu and Nash equilibria and provide an analytic expression for it. (Note that inefficient allocation of risk in symmetric-information thin market models may also occur when securities are exogenously given; see e.g. [25]. When securities are endogenously designed, [14] highlights that imperfect competition among issuers results in risk-sharing inefficiency, even if securities are traded among perfectly competitive investors.)
One may wonder whether the revealed agents’ subjective beliefs in a Nash equilibrium are far from their actual subjective probability measures, which would be unappealing from a modelling viewpoint. Extreme departures from actual beliefs are endogenously excluded in our model, as the distance of the truth from reported beliefs in a Nash equilibrium admits a priori bounds. Even though agents are free to choose any probability measure that supposedly represents their beliefs in a risk-sharing transaction and they do indeed end up choosing probability measures different from their actual ones, this departure cannot be arbitrarily large if the market is to reach equilibrium.
Turning our attention to Nash-equilibrium valuation, we show that the pricing probability measure can be written as a convex combination of the individual agents’ marginal indifference valuation measures. The weights of this convex combination depend on agents’ relative risk-tolerance coefficients, and as it turns out, the Nash-equilibrium valuation measure is closer to the marginal valuation measure of the more risk-averse agents. This fact highlights the importance of risk-tolerance coefficients in assessing the gain or loss of utility for individual agents in a Nash risk-sharing equilibrium; in fact, it implies that more risk-tolerant agents tend to get better cash compensation as a result of the Nash game than what they would get in an Arrow–Debreu equilibrium.
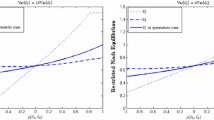
Inspired by the involvement of the risk-tolerance coefficients in the agents’ utility gain or loss, in Sect. 5, we focus on induced Arrow–Debreu and Nash equilibria of two-agent games when one of the agents’ preferences approaches risk-neutrality. We first establish that both equilibria converge to well-defined limits. Notably, it is shown that an extremely risk-tolerant agent drives the market to the same equilibrium regardless of whether the other agent acts strategically or plainly submits true subjective beliefs. In other words, extremely risk-tolerant agents tend to dominate the risk-sharing transaction. The study of limiting equilibria indicates that although there is a loss of aggregate utility when agents act strategically, there is always a utility gain in the Nash transaction compared to an Arrow–Debreu equilibrium for the extremely risk-tolerant agent, regardless of the risk-tolerance level and subjective beliefs of the other agent. Extremely risk-tolerant agents are willing to undertake more risk in exchange for better cash compensation; under the risk-sharing game, they respond to the risk-averse agent’s hedging needs and beliefs by driving the market to a higher price for the security they short. This implies that agents with sufficiently high risk-tolerance—although still not risk-neutral—will prefer thin markets. The case where both acting agents uniformly approach risk-neutrality is also treated, where it is shown that the limiting Nash equilibrium securities equal half of the limiting Arrow–Debreu equilibrium securities, hinting towards the fact that a Nash risk-sharing equilibrium results in loss of trading volume.
For convenience of reading, all the proofs of the paper are placed in the Appendix.
2 Optimal sharing of risk
2.1 Notation
The symbols \(\mathbf{N}\) and \(\mathbf{R}\) are used to denote the sets of all natural and real numbers, respectively. We have chosen to use the symbol ℝ to denote (reported, or revealed) probabilities.
In all that follows, random variables are defined on a probability space \((\Omega , \, \mathcal{F}, \, \mathbb{P})\). We stress that no finiteness restriction is enforced on the state space \(\Omega \). We use \(\mathcal{P}\) for the class of all probabilities that are equivalent to the baseline probability ℙ. For \(\mathbb{Q}\in \mathcal{P}\), we use \(\mathbb{E}_{\mathbb{Q}}\) to denote the expectation under ℚ. The space \(\mathbb{L}^{0}\) consists of all (equivalence classes, modulo almost sure equality) finite-valued random variables with the topology of convergence in probability. This topology does not depend on the representative probability from \(\mathcal{P}\), and \(\mathbb{L}^{0}\) may be infinite-dimensional. For \(\mathbb{Q}\in \mathcal{P}\), \(\mathbb{L}^{1} (\mathbb{Q})\) consists of all \(X \in \mathbb{L}^{0}\) with \(\mathbb{E}_{\mathbb{Q}}\left[ |X|\right] < \infty \). We use \(\mathbb{L}^{\infty }\) for the subset of \(\mathbb{L} ^{0}\) consisting of essentially bounded random variables.
Whenever \(\mathbb{Q}_{1} \in \mathcal{P}\) and \(\mathbb{Q}_{2} \in \mathcal{P}\), \(\mathrm{d}\mathbb{Q}_{2} / \mathrm{d}\mathbb{Q}_{1}\) denotes the (strictly positive) density of \(\mathbb{Q}_{2}\) with respect to \(\mathbb{Q}_{1}\). The relative entropy of \(\mathbb{Q}_{2} \in \mathcal{P}\) with respect to \(\mathbb{Q}_{1} \in \mathcal{P}\) is defined as
For \(X \in \mathbb{L}^{0}\) and \(Y \in \mathbb{L}^{0}\), we write \(X \sim Y\) when there exists \(c \in \mathbf{R}\) such that \(Y = X + c\). In particular, this notion of equivalence will ease notation on probability densities: for \(\mathbb{Q}_{1} \in \mathcal{P}\) and \(\mathbb{Q}_{2} \in \mathcal{P}\), we write \(\log \left( \mathrm{d} \mathbb{Q}_{2} / \mathrm{d}\mathbb{Q}_{1}\right) \sim \Lambda \) to mean that \(\exp (\Lambda ) \in \mathbb{L}^{1} (\mathbb{Q}_{1})\) and \(\mathrm{d}\mathbb{Q}_{2} / \mathrm{d}\mathbb{Q}_{1} = (\mathbb{E} _{\mathbb{Q}_{1}} [\exp (\Lambda )])^{-1} \exp (\Lambda )\).
2.2 Agents and preferences
We consider a market with a single future period, at which point all uncertainty is resolved. In this market, there are \(n + 1\) economic agents, where \(n \in \mathbf{N}\); for concreteness, define the index set \(I = \left\{ 0, \ldots , n\right\} \). Agents derive utility only from the consumption of a numéraire in the future, and all considered security payoffs are expressed in units of this numéraire. In particular, future deterministic amounts have the same present value for the agents. The preference structure of agent \(i \in I\) over future random outcomes is numerically represented via the concave exponential utility functional
where \(\delta_{i} \in (0, \infty )\) is the agent’s risk-tolerance, and \(\mathbb{P}_{i} \in \mathcal{P}\) represents the agent’s subjective beliefs. For any \(X \in \mathbb{L}^{0}\), agent \(i \in I\) is indifferent between the cash amount \(\mathbb{U} _{i} (X)\) and the corresponding risky position \(X\); in other words, \(\mathbb{U}_{i} (X)\) is the certainty equivalent of \(X \in \mathbb{L}^{0}\) for agent \(i \in I\). The functional \(- \mathbb{U}_{i}\) is an entropic risk measure in the terminology of convex risk measure literature; see, for example, [18, Chap. 4].
Define the aggregate risk-tolerance \(\delta \mathrel{\mathop{:}}= \sum_{i \in I}\delta_{i}\) and the relative risk-tolerance \(\lambda _{i} \mathrel{\mathop{:}}=\delta_{i} / \delta \) for all \(i \in I\). Note that \(\sum_{i \in I}\lambda_{i} = 1\). Finally, set \(\delta_{-i} \mathrel{ \mathop{:}}=\delta - \delta_{i}\) and \(\lambda_{-i} \mathrel{ \mathop{:}}=1 - \lambda_{i}\) for all \(i \in I\).
2.3 Subjective probabilities and endowments
Preference structures that are numerically represented via (2.1) are rich enough to include the possibility of already existing portfolios of random positions for acting agents. To wit, suppose that \(\widetilde{\mathbb{P}}_{i}\in \mathcal{P}\) are the actual subjective beliefs of agent \(i \in I\), who also carries a risky future payoff in units of the numéraire. Following standard terminology, we call this cumulative (up to the point of resolution of uncertainty) payoff random endowment and denote it by \(E_{i} \in \mathbb{L}^{0}\). In this setup, adding on top of \(E_{i}\) a payoff \(X \in \mathbb{L}^{0}\) for agent \(i \in I\) results in a numerical utility equal to \(\widetilde{\mathbb{U}}_{i}(X) \mathrel{ \mathop{:}}=- \delta_{i} \log \mathbb{E}_{\widetilde{\mathbb{P}}_{i}} [\exp (- (X+E_{i}) / \delta_{i}])\). Assume that \(\widetilde{\mathbb{U}}_{i}(0) > - \infty \), that is, that \(\exp (- E _{i} / \delta_{i}) \in \mathbb{L}^{1} ( \widetilde{\mathbb{P}}_{i} )\). Defining \(\mathbb{P}_{i} \in \mathcal{P}\) via \(\log ( \mathrm{d} \mathbb{P}_{i} / \mathrm{d}\widetilde{\mathbb{P}}_{i} ) \sim - E_{i} / \delta_{i}\) and \(\mathbb{U}_{i}\) by (2.1), we have that \(\mathbb{U}_{i}(X) = \widetilde{\mathbb{U}}_{i}(X) - \widetilde{\mathbb{U}}_{i}(0)\) for all \(X \in \mathbb{L}^{0}\). Hence, hereafter, the probability \(\mathbb{P}_{i}\) is understood to incorporate any possible random endowment of agent \(i \in I\), and the utility is measured in relative terms as the difference from the baseline level \(\widetilde{\mathbb{U}}_{i}(0)\).
Taking the above discussion into account, we stress that agents are completely characterised by their risk-tolerance level and (endowment-modified) subjective beliefs, that is, by the collection of pairs \((\delta_{i}, \mathbb{P}_{i})_{i \in I}\). In other aspects, and unless otherwise noted, agents are considered symmetric (regarding information, bargaining power, cost of risk-sharing participation, etc.).
2.4 Geometric-mean probability
We introduce a method that produces a geometric mean of probabilities, which will play a central role in our discussion. Fix \((\mathbb{R} _{i})_{i \in I} \in \mathcal{P}^{I}\). In view of Hölder’s inequality, we have \(\prod_{i \in I} \left( \mathrm{d}\mathbb{R}_{i} / \mathrm{d}\mathbb{P}\right) ^{\lambda_{i}} \in \mathbb{L}^{1}( \mathbb{P})\). Therefore, we may define \(\mathbb{Q}\in \mathcal{P}\) via \(\log \left( \mathrm{d}\mathbb{Q}/ \mathrm{d}\mathbb{P}\right) \sim \sum_{i \in I} \lambda_{i} \log \left( \mathrm{d}\mathbb{R}_{i} / \mathrm{d}\mathbb{P}\right) \). Since \(\sum_{i \in I} \lambda_{i} \log \left( \mathrm{d}\mathbb{R}_{i} / \mathrm{d}\mathbb{Q}\right) \sim 0\), we are allowed to formally write
The fact that \(\mathrm{d}\mathbb{R}_{i} / \mathrm{d}\mathbb{Q}\in \mathbb{L}^{1}(\mathbb{Q})\) implies \(\log^{+} \left( \mathrm{d} \mathbb{R}_{i} / \mathrm{d}\mathbb{Q}\right) \in \mathbb{L}^{1}( \mathbb{Q})\) and Jensen’s inequality give \(\mathbb{E}_{\mathbb{Q}}[ \log \left( \mathrm{d}\mathbb{R}_{i} / \mathrm{d}\mathbb{Q}\right) ] \leq 0\) for all \(i \in I\). Note that (2.2) implies the existence of \(c \in \mathbf{R}\) such that \(\sum_{i \in I} \lambda _{i} \log \left( \mathrm{d}\mathbb{R}_{i} / \mathrm{d}\mathbb{Q}\right) = c\); therefore, we in fact have \(\mathbb{E}_{\mathbb{Q}}[\log \left( \mathrm{d} \mathbb{R}_{i} / \mathrm{d}\mathbb{Q}\right) ] \in (- \infty , 0]\) for all \(i \in I\). In particular, \(\log \left( \mathrm{d}\mathbb{R}_{i} / \mathrm{d}\mathbb{Q}\right) \in \mathbb{L}^{1}(\mathbb{Q})\) for all \(i \in I\), and
2.5 Securities and valuation
Discrepancies amongst agents’ preferences provide incentive to design securities, the trading of which could be mutually beneficial in terms of risk reduction. In principle, the ability to design and trade securities in any desirable way essentially leads to a complete market. In such a market, transactions amongst agents are characterised by a valuation measure (that assigns prices to all imaginable securities) and a collection of securities that will actually be traded. Since all future payoffs are measured under the same numéraire, (no-arbitrage) valuation corresponds to taking expectations with respect to probabilities in \(\mathcal{P}\). Given a valuation measure, agents agree on a collection \((C_{i})_{i \in I} \in (\mathbb{L}^{0})^{I}\) of zero-value securities satisfying the market clearing condition \(\sum_{i \in I} C_{i} = 0\). The security that agent \(i \in I\) takes a long position in as part of the transaction is \(C_{i}\).
As mentioned in the introductory section, our model can find applications in OTC markets. For instance, the design of asset-backed securities involves only a small number of financial institutions; in this case, \(\mathbb{P}_{i}\) stands for the subjective beliefs of each institution \(i \in I\) and, in view of the discussion of Sect. 2.3, further incorporates any existing portfolios that back the security payoffs. In order to share their risky positions, the institutions agree on prices of future random payoffs and on the securities they are going to exchange. Other examples are the market of innovated credit derivatives or the market of asset swaps that involve exchanging a random payoff and a fixed payment.
2.6 Arrow–Debreu equilibrium
In the absence of any kind of strategic behaviour in designing securities, the agreed-upon transaction amongst agents will actually form an Arrow–Debreu equilibrium. The valuation measure will determine both trading and indifference prices, and securities will be constructed in a way that maximises each agent’s respective utility.
Definition 2.1
\((\mathbb{Q}^{\ast }, (C^{\ast }_{i})_{i \in I}) \in \mathcal{P} \times (\mathbb{L}^{0})^{I}\) is called an Arrow–Debreu equilibrium if
-
1.
\(\sum_{i \in I}C^{\ast }_{i} = 0\), and \(C^{\ast }_{i} \in \mathbb{L} ^{1}(\mathbb{Q}^{\ast })\) and \(\mathbb{E}_{\mathbb{Q}^{\ast }} [C^{ \ast }_{i}] = 0\) for all \(i \in I\); and
-
2.
for all \(C \in \mathbb{L}^{1} (\mathbb{Q}^{\ast })\) with \(\mathbb{E} _{\mathbb{Q}^{\ast }}\left[ C\right] \leq 0\), \(\mathbb{U}_{i} (C) \leq \mathbb{U}_{i} (C^{\ast }_{i})\) for all \(i \in I\).
Under risk preferences modelled by (2.1), a unique Arrow–Debreu equilibrium can be explicitly obtained. In other guises, Theorem 2.2 that follows has appeared in many works; see, for instance, [10, 13, 12]. Its proof is based on standard arguments; however, for reasons of completeness, we provide a short argument in Sect. A.1.
Theorem 2.2
In the above setting, there exists a unique Arrow–Debreu equilibrium \((\mathbb{Q}^{\ast }, (C^{\ast }_{i})_{i \in I})\). In fact, the valuation measure \(\mathbb{Q}^{\ast }\in \mathcal{P}\) is such that
and the equilibrium market-clearing securities \((C^{\ast }_{i})_{i \in I} \in (\mathbb{L}^{0})^{I}\) are given by
where the fact that \(\mathcal{H}(\mathbb{Q}^{\ast }\, | \,\mathbb{P} _{i} ) < \infty \) for all \(i \in I\) follows from Sect. 2.4.
The securities that agents obtain at an Arrow–Debreu equilibrium described in (2.4) provide higher payoffs on events where their individual subjective probabilities are higher than the “geometric mean” probability \(\mathbb{Q}^{\ast }\) of (2.3). In other words, discrepancies in beliefs result in allocations where agents receive higher payoffs on their corresponding relatively more likely events.
Let us note an interesting decomposition for the securities traded at an Arrow–Debreu equilibrium. To wit, in view of the string of equalities
agent \(i\) is indifferent between no trading and the first “random” part \(\delta_{i} \log (\mathrm{d}\mathbb{P}_{i} / \mathrm{d} \mathbb{Q}^{\ast })\) of the security \(C^{\ast }_{i}\). The second “cash” part \(\delta_{i} \mathcal{H}(\mathbb{Q}^{\ast }\, | \, \mathbb{P}_{i} )\) of \(C^{\ast }_{i}\) is always nonnegative and represents the monetary gain of agent \(i\) resulting from the Arrow–Debreu transaction. After this transaction, the position of agent \(i\) has certainty equivalent
The aggregate monetary value resulting from the Arrow–Debreu transaction equals
Remark 2.3
In the setting and notation of Sect. 2.3, let \((E_{i})_{i \in I}\) be the collection of agents’ random endowments. Furthermore, suppose that agents share common subjective beliefs; for concreteness, assume that \(\widetilde{\mathbb{P}}_{i} = \mathbb{P}\) for all \(i \in I\). In this case, setting \(E\mathrel{\mathop{:}}= \sum_{i \in I}E_{i}\), the equilibrium valuation measure from (2.3) satisfies \(\log \left( \mathrm{d}\mathbb{Q}^{ \ast }/ \mathrm{d}\mathbb{P}\right) \sim -E/\delta \), and the equilibrium securities from (2.4) are given by \(C^{\ast }_{i} = \lambda_{i} E - E_{i} - \mathbb{E}_{\mathbb{Q}^{ \ast }}\left[ \lambda_{i} E - E_{i}\right] \) for all \(i \in I\). In particular, note the well-known fact that the payoff of each shared security is a linear combination of the agents’ random endowments.
Remark 2.4
Since \(C^{\ast }_{i} / \delta_{i} \sim - \log (\mathrm{d}\mathbb{Q} ^{\ast }/ \mathrm{d}\mathbb{P}_{i})\), it is straightforward to compute
In particular, for \(C_{i} \in \mathbb{L}^{1}(\mathbb{Q}^{\ast })\), an application of Jensen’s inequality gives
with equality if and only if \(C_{i} \sim C^{\ast }_{i}\). The last inequality shows that \(C^{\ast }_{i}\) is indeed the optimally designed security for agent \(i \in I\) under the valuation measure \(\mathbb{Q} ^{\ast }\). Furthermore, for any collection \((C_{i})_{i \in I}\) with \(\sum_{i \in I} C_{i} = 0\) and \(C_{i} \in \mathbb{L}^{1}(\mathbb{Q} ^{\ast })\) for all \(i \in I\), it follows that \(\sum_{i \in I} \mathbb{U}_{i} (C_{i}) \leq \sum_{i \in I} \mathbb{U}_{i} (C^{\ast } _{i}) = u^{\ast }\). A standard argument using the monotone convergence theorem extends the previous inequality to
with equality if and only if \(C_{i} \sim C^{\ast }_{i}\) for all \(i \in I\). Therefore, \((C^{\ast }_{i})_{i \in I}\) is a maximiser of the functional \(\sum_{i \in I} \mathbb{U}_{i} (C_{i})\) over all \((C_{i})_{i \in I} \in (\mathbb{L}^{0})^{I}\) with \(\sum_{i \in I} C _{i} = 0\). In fact, the collection of all such maximisers is \((z_{i} + C^{\ast }_{i})_{i \in I}\), where \((z_{i})_{i \in I} \in \mathbf{R}^{I}\) is such that \(\sum_{i \in I}z_{i} = 0\). It can be shown that all Pareto-optimal securities are exactly of this form; see e.g. [19, Thm. 3.1] for a more general result. Because of this Pareto optimality, the collection \((\mathbb{Q}^{\ast }, (C ^{\ast }_{i})_{i \in I})\) usually comes under the appellation of (welfare) optimal securities and valuation measure, respectively.
Of course, not every Pareto-optimal allocation \((z_{i} + C^{\ast } _{i})_{i \in I}\), where \((z_{i})_{i \in I}\) is such that \(\sum_{i \in I}z_{i} = 0\), is economically reasonable. A minimal “fairness” requirement that has to be imposed is that the position of each agent after the transaction is at least as good as the initial state. Since the utility comes only at the terminal time, we obtain the requirement \(z_{i} \geq - u^{\ast }_{i}\) for all \(i \in I\). Whereas there may be many choices satisfying the latter requirement in general, the choice \(z_{i} = 0\) of Theorem 2.2 has the cleanest economic interpretation in terms of a complete financial market equilibrium.
Remark 2.5
If we ignore potential transaction costs, the cases where an agent has no motive to enter a risk-sharing transaction are extremely rare. Indeed, agent \(i\) will not take part in the Arrow–Debreu transaction if and only if \(C_{i} = 0\), which happens when \(\mathbb{P}_{i} = \mathbb{Q}^{\ast }\). In particular, agents will already be in an Arrow–Debreu equilibrium, and no transaction will take place if and only if they all share the same subjective beliefs.
3 Agents’ best probability response
3.1 Strategic behaviour in risk sharing
In the Arrow–Debreu setting, the resulting equilibrium is based on the assumption that agents do not apply any kind of strategic behaviour. However, in the majority of practical risk-sharing situations, the modelling assumption of absence of agents’ strategic behaviour is unreasonable, resulting amongst other things in overestimation of market efficiency. When securities are negotiated among agents, their design and valuation depend not only on their existing risky portfolios, but also on the beliefs about the future outcomes they report for sharing. In general, agents have an incentive to report subjective beliefs that may differ from their true views about future uncertainty; in fact, these also depend on subjective beliefs reported by the other parties.
As discussed in Sect. 2.6, for a given set of agents’ subjective beliefs, the optimal sharing rules are governed by the mechanism resulting in an Arrow–Debreu equilibrium, as these are the rules that efficiently allocate discrepancies of risks and beliefs among agents. It is then reasonable to assume that in the absence of a social planner, agents adapt this sharing mechanism for any collection \((\mathbb{R}_{i})_{i \in I} \in \mathcal{P}^{I}\) of subjective probabilities they choose to report; see also the related discussion in the introductory section. More precisely, in accordance to (2.3) and (2.4), the agreed-upon valuation measure \(\mathbb{Q}\in \mathcal{P}\) is such that \(\log \mathrm{d} \mathbb{Q}\sim \sum_{i \in I}\lambda_{i} \log \mathrm{d}\mathbb{R} _{i}\), and the collection of securities that agents will trade are \(C_{i} \mathrel{\mathop{:}}=\delta_{i} \log (\mathrm{d}\mathbb{R}_{i} / \mathrm{d}\mathbb{Q}) + \delta_{i} \mathcal{H}(\mathbb{Q}\, | \, \mathbb{R}_{i} )\), \(i \in I\).
Given the sharing rules consistent with an Arrow–Debreu equilibrium, agents respond to subjective beliefs that other agents have reported, with the goal to maximise their individual utility. In this way, a game is formed with the probability family \(\mathcal{P}\) being the agents’ set of strategic choices. The subject of the present Sect. 3 is to analyse the behaviour of individual agents, establish their best response problem, and show its well-posedness. The definition and analysis of the Nash risk-sharing equilibrium is taken up in Sect. 4.
3.2 Best response
We now describe how agents respond to the reported subjective probability assessments from their counterparties. For the purposes of Sect. 3.2, we fix an agent \(i \in I\) and a collection \(\mathbb{R}_{-i} \mathrel{\mathop{:}}=(\mathbb{R}_{j})_{j \in I \setminus \left\{ i\right\} } \in \mathcal{P}^{I \setminus \left\{ i\right\} }\) of reported probabilities of the remaining agents and seek the subjective probability that is going to be submitted by agent \(i \in I\). According to the rules described in Sect. 3.1, a reported probability \(\mathbb{R}_{i} \in \mathcal{P}\) from agent \(i \in I\) leads to entering a long position on the security with payoff
where \(\mathbb{Q}^{(\mathbb{R}_{-i}, \mathbb{R}_{i})} \in \mathcal{P}\) is such that
By reporting subjective beliefs \(\mathbb{R}_{i} \in \mathcal{P}\), agent \(i \in I\) also indirectly affects the geometric-mean valuation probability \(\mathbb{Q}^{(\mathbb{R}_{-i}, \mathbb{R}_{i})}\), resulting in a highly nonlinear overall effect on the security \(C_{i}\). With the above understanding, and given \(\mathbb{R}_{-i} \in \mathcal{P}^{I \setminus \left\{ i\right\} }\), the response function of agent \(i \in I\) is defined to be
where \(\mathcal{H}(\mathbb{Q}^{(\mathbb{R}_{-i}, \mathbb{R}_{i})} \, | \,\mathbb{R}_{i} ) < \infty \) follows from the discussion of Sect. 2.4. The problem of agent \(i\) is to report the subjective probability that maximises the certainty equivalent of the resulting position after the transaction, that is, to identify \(\mathbb{R}^{\mathrm{r}}_{i} \in \mathcal{P}\) such that
Any \(\mathbb{R}^{\mathrm{r}}_{i} \in \mathcal{P}\) satisfying (3.1) is called a best probability response.
In contrast to the majority of the related literature, the agent’s strategic set of choices in our model may be of infinite dimension. This generalisation is important from a methodological viewpoint; for example, in the setting of Sect. 2.3, it allows for random endowments with infinite support, like ones with a Gaussian distribution or arbitrarily fat tails, a substantial feature in the modelling of risk.
Remark 3.1
The best response problem (3.1) imposes no constrains on the shape of the agent’s reported subjective probability as long as it belongs to \(\mathcal{P}\). In principle, it is possible for agents to report subjective views that are far from their actual ones. Such severe departures may be deemed unrealistic and are undesirable from a modelling point of view. However, as will be argued in Sect. 4.3.2, extreme responses are endogenously excluded in our setup.
We show in the sequel (Theorem 3.7) that best responses in (3.1) exist and are unique. We start with a result that gives necessary and sufficient conditions for a best probability response.
Proposition 3.2
Fix \(i \in I\) and \(\mathbb{R}_{-i} \in \mathcal{P}^{I \setminus \left\{ i\right\} }\). Then \(\mathbb{R}^{\mathrm{r}}_{i} \in \mathcal{P}\) is a best probability response for agent \(i\) given \(\mathbb{R}_{-i}\) if and only if the random variable
satisfies the bound \(C^{\mathrm{r}}_{i} > - \delta_{-i}\) and
The proof of Proposition 3.2 is given in Sect. A.2. The necessity of the stated conditions for a best response follows from the first-order optimality conditions. Establishing the sufficiency of the stated conditions is nontrivial due to the fact that it is far from clear (and in fact not known to us) whether the response function is concave.
Remark 3.3
In the context of Proposition 3.2, rewriting (3.2), we obtain that
Using also the fact that \(C^{\mathrm{r}}_{i} / \delta_{i} \sim \log ( \mathrm{d}\mathbb{R}^{\mathrm{r}}_{i} / \mathrm{d}\mathbb{Q}^{( \mathbb{R}_{-i}, \mathbb{R}^{\mathrm{r}}_{i})} )\), it follows that
Hence \(\mathbb{R}^{\mathrm{r}}_{i} = \mathbb{P}_{i}\) if and only if \(\log (1 + C^{\mathrm{r}}_{i} / \delta_{-i} ) \sim 0\), which holds if and only if \(C^{\mathrm{r}}_{i} = 0\). (Note that \(C^{\mathrm{r}}_{i} \sim 0\) implies \(C^{\mathrm{r}}_{i} = 0\) since the expectation of \(C^{\mathrm{r}}_{i}\) under \(\mathbb{Q}^{(\mathbb{R}_{-i}, \mathbb{R} ^{\mathrm{r}}_{i})}\) equals zero.) In words, the best probability response and actual subjective probability of an agent agree if and only if the agent has no incentive to participate in the risk-sharing transaction, given the reported subjective beliefs of other agents. Hence, in any nontrivial cases, agents’ strategic behaviour implies a departure from reporting their true beliefs.
Plugging (3.4) back to (3.3) and using also (3.2), we obtain
providing directly the valuation measure \(\mathbb{Q}^{(\mathbb{R}_{-i}, \mathbb{R}^{\mathrm{r}}_{i})}\) in terms of the security \(C^{ \mathrm{r}}_{i}\).
Remark 3.4
A message from (3.4) is that according to their best response process, agents report beliefs that understate (resp. overstate) the probability of their payoff being high (resp. low) relatively to their true beliefs. Such behaviour is clearly driven by a desired post-transaction utility increase.
More importantly and in sharp contrast to the securities \((C^{\ast } _{i})_{i \in I}\) formed in an Arrow–Debreu equilibrium, the security that agent \(i \in I\) wishes to enter, after taking into account the aggregate reported beliefs of the rest and declaring subjective probability \(\mathbb{R}^{\mathrm{r}}_{i}\), has limited liability as it is bounded from below by the constant \(-\delta_{-i}\).
Remark 3.5
Additional insight regarding best probability responses may be obtained by resorting to the discussion of Sect. 2.3, where \(\mathbb{P}_{i}\) incorporates the random endowment \(E_{i} \in \mathbb{L}^{0}\) of agent \(i \in I\) in the sense that \(\log ( \mathrm{d}\mathbb{P}_{i} / \mathrm{d}\widetilde{\mathbb{P}}_{i} ) \sim - E_{i}/\delta_{i}\), where \(\widetilde{\mathbb{P}}_{i}\) denotes the subjective probability of agent \(i\). It follows from (3.4) that
It then becomes apparent that when agents share their risky endowment, they tend to put more weight on the probability of the downside of their risky exposure rather than the upside. For an illustrative situation, see Example 3.8 later on.
Remark 3.6
In the course of the proof of Proposition 3.2, the constant in the equivalence (3.2) is explicitly computed; see (A.3). This constant has a particularly nice economic interpretation in the case of two agents. To wit, let \(I = \left\{ 0,1\right\} \) and suppose that \(\mathbb{R}_{1} \in \mathcal{P}\) is given. Then from the vantage point of agent 0, (3.2) becomes
where the constant \(\zeta_{0} \in \mathbf{R}\) is such that
where \(\mathbb{U}_{1} (\cdot ; \mathbb{R}_{1})\) denotes the utility functional of a “fictitious” agent with representative pair \((\delta_{1}, \mathbb{R}_{1})\). In words, \(\zeta_{0}\) is the post-transaction difference, denominated in units of risk-tolerance, of the utility of agent 0 from the utility of agent 1 (who obtains the security \(- C^{\mathrm{r}}_{0}\)), provided that the latter utility is measured with respect to the reported, as opposed to subjective, beliefs of agent 1. In particular, when agent 1 does not behave strategically, in which case \(\mathbb{R}_{1} = \mathbb{P}_{1}\), it holds that \(\zeta_{0} = \mathbb{U}_{0} (C^{\mathrm{r}}_{0}) / \delta_{0} - \mathbb{U}_{1} (-C^{\mathrm{r}}_{0}) / \delta_{1}\).
Proposition 3.2 sets a roadmap for proving the existence and uniqueness in the best response problem via a one-dimensional parameterisation. Indeed, in accordance to (3.2), to find a best response, we consider for each \(z_{i} \in \mathbf{R}\) the unique random variable \(C_{i}(z_{i})\) that satisfies the equation
Then, upon defining \(\mathbb{Q}_{i} (z_{i})\) via
in accordance to (3.5), we seek \(\widehat{z}_{i} \in \mathbf{R}\) such that \(C_{i}(\widehat{z}_{i}) \in \mathbb{L}^{1}(\mathbb{Q}_{i}(\widehat{z}_{i}))\) and \(\mathbb{E} _{\mathbb{Q}_{i}(\widehat{z}_{i})} \left[ C_{i}(\widehat{z}_{i})\right] = 0\). It turns out that there is a unique such choice; once found, we simply define \(\mathbb{R}^{\mathrm{r}}_{i}\) via \(\log (\mathrm{d} \mathbb{R}^{\mathrm{r}}_{i} / \mathrm{d}\mathbb{P}_{i}) \sim - \log \left( 1 + C_{i}(\widehat{z}_{i}) / \delta_{-i} \right) \), in accordance to (3.4), to obtain the unique best response of agent \(i \in I\) given \(\mathbb{R}_{-i}\). The technical details of the proof of Theorem 3.7 below are given in Sect. A.3.
Theorem 3.7
For \(i \in I\) and \(\mathbb{R}_{-i} \in \mathcal{P}^{I \setminus \left\{ i\right\} }\), there exists a unique \(\mathbb{R}^{ \mathrm{r}}_{i} \in \mathcal{P}\) such that \(\mathbb{V}_{i} ( \mathbb{R}^{\mathrm{r}}_{i}; \mathbb{R}_{-i}) = \sup_{\mathbb{R}_{i} \in \mathcal{P}} \mathbb{V}_{i} (\mathbb{R}_{i}; \mathbb{R}_{-i})\).
3.3 The value of strategic behaviour
The increase in agents’ utility caused by following the best probability response procedure can be regarded as a measure for the value of the strategic behaviour induced by problem (3.1). Consider, for example, the case where only a single agent (say) \(0 \in I\) applies the best probability response strategy and the rest of the agents report their true beliefs, that is, \(\mathbb{R}_{j} = \mathbb{P}_{j}\) for \(j \in I \setminus \left\{ 0\right\} \). As mentioned in the introductory section, this is a potential model of a transaction where only agent 0 possesses meaningful market power. Based on the results of Sect. 3.2, we may calculate the gains, relative to the Arrow–Debreu transaction, that agent 0 obtains by incorporating such strategic behaviour (which, among others, implies limited liability of the security the agent takes a long position in). The main insights are illustrated in the following two-agent example.
Example 3.8
Suppose that \(I = \left\{ 0,1\right\} \) and \(\delta_{0} = 1 = \delta _{1}\). We use the setup of Sect. 2.3, where for simplicity it is assumed that agents have the same subjective probability measure. The agents are exposed to random endowments \(E_{0}\) and \(E_{1}\) that (under the common probability measure) have Gaussian laws with mean zero and common variance \(\sigma^{2} > 0\), whereas \(\rho \in [-1,1]\) denotes the correlation coefficient of \(E_{0}\) and \(E_{1}\). In this case, it is straightforward to check that \(C^{\ast }_{0} = (E_{1}-E_{0})/2\); therefore, after the Arrow–Debreu transaction, the position of agent 0 is \(E_{0} + C^{\ast }_{0} = (E _{0} + E_{1}) / 2\). On the other hand, if agent 1 reports true beliefs, then by (3.2) the security \(C^{\mathrm{r}}_{0}\) corresponding to the best probability response of agent 0 should satisfy \(2 C^{\mathrm{r}}_{0} + \log (1 + C^{\mathrm{r}}_{0}) = \zeta _{0} +E_{1}\) for an appropriate \(\zeta_{0} \in \mathbf{R}\) that is coupled with \(C^{\mathrm{r}}_{0}\). For \(\sigma^{2} = 1\) and \(\rho = -0.5\), straightforward Monte Carlo simulation allows the numerical approximation of the probability density function (pdf) of \(E_{0}\) and \(E_{1}\) under the best response probability \(\mathbb{R} ^{\mathrm{r}}_{0}\), illustrated in Fig. 1. As is apparent, the best probability response drives agent 0 to overstate the downside risk of \(E_{0}\) and understate the downside risk of \(E_{1}\).
The solid black line is the pdf of endowments \(E_{0}\) and \(E_{1}\) under the agents’ common subjective probability measure, whereas the other curves illustrate the pdf of \(E_{0}\) (dashed blue) and \(E_{1}\) (dotted red) under the best probability response of agent 0. In this example, \(\sigma^{2} = 1\) and \(\rho =-0.5\)
The effect of following such a strategic behaviour is depicted in Fig. 2, where we compare the probability density functions of the positions of agent 0 under (i) no trading, (ii) the Arrow–Debreu transaction, and (iii) the transaction following the application of best response strategic behaviour. Compared to the Arrow–Debreu position, the lower bound of the security \(C^{\mathrm{r}}_{0}\) guarantees a heavier right tail of the agent’s position after the best response transaction.
The solid black line is the pdf of the initial position \(E_{0}\), the dashed blue line illustrates the pdf of the position \(E_{0}+C^{\ast }_{0}\), and the dotted red line is the pdf of the position \(E_{0}+C^{\mathrm{r}}_{0}\), all under the common subjective probability measure. In this example, \(\sigma^{2} = 1\) and \(\rho =-0.5\)
4 Nash risk-sharing equilibrium
We now consider the situation where every single agent follows the same strategic behaviour indicated by the best response problem of Sect. 3. As previously mentioned, sharing securities are designed following the sharing rules determined by Theorem 2.2 for any collection of reported subjective views. With the well-posedness of the best response problem established, we are now ready to examine whether the game among agents has an equilibrium point. In view of the analysis of Sect. 3, individual agents have a motive to declare subjective beliefs different from the actual ones. (In particular, in the setting of Sect. 2.3, agents tend to overstate the probability of their random endowments taking low values.) Each agent acts according to the best response mechanism as in (3.1), given what other agents have reported as subjective beliefs. In a sense, the best response mechanism indicates a negotiation scheme, the fixed point (if one exists) of which produces the Nash equilibrium valuation measure and risk-sharing securities.
Let us emphasise that the actual subjective beliefs of individual players are not necessarily assumed to be private knowledge; rather, it is assumed here that agents have agreed upon the rules that associate any reported subjective beliefs to securities and prices, even if the reported beliefs are not the actual ones. In fact, even if subjective beliefs constitute private knowledge initially, some information about them will necessarily be revealed in the negotiation process that leads to a Nash equilibrium.
There are two relevant points to consider here. Firstly, it is unreasonable for participants to attempt to invalidate the negotiation process based on the claim that other parties do not report their true beliefs, as the latter is after all a subjective matter. This particular point is reinforced from the a posteriori fact that reported subjective beliefs in a Nash equilibrium do not deviate far from the true ones, as was pointed out in Remark 3.1 and is further elaborated in Sect. 4.3.2. Secondly, it is exactly the limited number of participants, rather than private or asymmetric information, that gives rise to strategic behaviour: agents recognise their ability to influence the market since securities and valuation become output of collective reported beliefs. Even under the appreciation that other agents will not report true beliefs and the negotiation will not produce an Arrow–Debreu equilibrium, agents still want to reach a Nash equilibrium as they will improve their initial position. In fact, transactions with a limited number of participants typically equilibrate far from their competitive equivalents, as has been also highlighted in other models of thin financial markets with symmetric information structure like the ones in [14] and [25]; see also the related discussion in the introductory section.
4.1 Revealed subjective beliefs
Considering the model from a more pragmatic point of view, we may argue that agents do not actually report subjective beliefs, but rather agree on a valuation measure \(\mathbb{Q}\in \mathcal{P}\) and zero-price sharing securities \((C_{i})_{i \in I}\) that clear the market. However, there is a one-to-one correspondence between reporting subjective beliefs and proposing a valuation measure and securities, as we describe below.
From the discussion of Sect. 3.1, a collection of subjective probabilities \((\mathbb{R}_{i})_{i \in I}\) gives rise to a valuation measure \(\mathbb{Q}\in \mathcal{P}\) such that \(\log \mathrm{d}\mathbb{Q}\sim \sum_{i \in I}\lambda_{i} \log \mathrm{d} \mathbb{R}_{i}\) and a collection \((C_{i})_{i \in I}\) of securities such that \(C_{i} = \delta_{i} \log (\mathrm{d}\mathbb{R}_{i} / \mathrm{d} \mathbb{Q}) + \delta_{i} \mathcal{H}(\mathbb{Q}\, | \,\mathbb{R}_{i} )\) for all \(i \in I\). Of course, \(\sum_{i \in I}C_{i} = 0\) and \(\mathbb{E}_{\mathbb{Q}}\left[ C_{i}\right] = 0\) for all \(i \in I\). A further technical observation is that \(\exp (C_{i} / \delta_{i}) \in \mathbb{L}^{1}(\mathbb{Q})\) for all \(i \in I\), which is then a necessary condition that an arbitrary collection of market-clearing securities \((C_{i})_{i \in I}\) must satisfy with respect to an arbitrary valuation probability \(\mathbb{Q}\in \mathcal{P}\) in order to be consistent with the aforementioned risk-sharing mechanism. The previous observations lead to a definition: for \(\mathbb{Q}\in \mathcal{P}\), we define the class \(\mathcal{C}_{\mathbb{Q}}\) of securities that clear the market and are consistent with the valuation measure ℚ via
Note that all expectations of \(C_{i}\) under ℚ in the definition of \(\mathcal{C}_{\mathbb{Q}}\) above are well defined. Indeed, the fact that \(\exp (C_{i} / \delta_{i}) \in \mathbb{L}^{1}( \mathbb{Q})\) in the definition of \(\mathcal{C}_{\mathbb{Q}}\) implies that \(C_{i}^{+} \in \mathbb{L}^{1}(\mathbb{Q})\) for all \(i \in I\). From \(\sum_{i \in I}C_{i} = 0\) we obtain \(\sum_{i \in I}\!|C_{i}| = 2 \sum_{i \in I}C_{i}^{+}\), and hence \(C_{i} \in \mathbb{L}^{1}(\mathbb{Q})\) for all \(i \in I\).
Given a valuation measure \(\mathbb{Q}\in \mathcal{P}\) and securities \((C_{i})_{i \in I} \in \mathcal{C}_{\mathbb{Q}}\), we may define a collection \((\mathbb{R}_{i})_{i \in I} \in \mathcal{P}^{I}\) via \(\log (\mathrm{d}\mathbb{R}_{i} / \mathrm{d}\mathbb{Q}) \sim C_{i} / \delta_{i}\) for \(i \in I\) and note that this is the unique collection in \(\mathcal{P}^{I}\) that results in the valuation probability \(\mathbb{Q}\in \mathcal{P}^{I}\) and securities \((C_{i})_{i \in I} \in \mathcal{C}_{\mathbb{Q}}\). In this way, the probabilities \((\mathbb{R}_{i})_{i \in I} \in \mathcal{P}^{I}\) can be considered as revealed by the valuation measure \(\mathbb{Q}\in \mathcal{P}\) and securities \((C_{i})_{i \in I} \in \mathcal{C}_{\mathbb{Q}}\). Hence, agents proposing risk-sharing securities and a valuation measure is equivalent to them reporting probability beliefs in the transaction. This viewpoint justifies and underlies Definition 4.1 that follows: the objects of a Nash equilibrium are the valuation measure and designed securities, in consistency with the definition of an Arrow–Debreu equilibrium.
4.2 Nash equilibrium and its characterisation
Following classic literature, we give the formal definition of a Nash risk-sharing equilibrium.
Definition 4.1
The collection \((\mathbb{Q}^{\diamond },(C^{\diamond }_{i})_{i \in I}) \in \mathcal{P}\times (\mathbb{L}^{0})^{I}\) is called a Nash equilibrium if \((C^{\diamond }_{i})_{i \in I} \in \mathcal{C}_{\mathbb{Q}^{\diamond }}\) and, with \(\log (\mathrm{d} \mathbb{R}^{\diamond }_{i} / \mathrm{d}\mathbb{Q}^{\diamond }) \sim C ^{\diamond }_{i} / \delta_{i}\) for all \(i \in I\) denoting the corresponding revealed subjective beliefs, it holds that
A use of Proposition 3.2 results in the characterisation Theorem 4.2, the proof of which is given in Sect. A.4. For this, we need to introduce the \(n\)-dimensional Euclidean space
Theorem 4.2
The collection \((\mathbb{Q}^{\diamond }, (C^{\diamond }_{i})_{i \in I}) \in \mathcal{P}\times (\mathbb{L}^{0})^{I}\) is a Nash equilibrium if and only if the following three conditions hold:
-
(N1)
\(C^{\diamond }_{i} > - \delta_{-i}\) for all \(i \in I\), and there exists \(z^{\diamond }= (z^{\diamond }_{i})_{i \in I} \in \Delta ^{I}\) such that
$$ C^{\diamond }_{i} + \delta_{i} \log \left( 1 + \frac{C^{\diamond }_{i}}{ \delta_{-i}} \right) = z^{\diamond }_{i} + C^{\ast }_{i} + \delta_{i} \sum_{j \in I} \lambda_{j} \log \bigg(1 + \frac{C^{\diamond }_{j}}{ \delta_{-j}} \bigg), \quad \forall i \in I; $$(4.2) -
(N2)
with \(\mathbb{Q}^{\ast }\in \mathcal{P}\) as in (2.3), that is, such that \(\log \mathrm{d}\mathbb{Q}^{\ast } \sim \sum_{i \in I}\lambda_{i} \log \mathrm{d}\mathbb{P}_{i}\), it holds that
$$ \log \frac{\mathrm{d}\mathbb{Q}^{\diamond }}{\mathrm{d}\mathbb{Q}^{ \ast }} \sim - \sum_{j \in I} \lambda_{j} \log \bigg(1 + \frac{C^{ \diamond }_{j}}{\delta_{-j}} \bigg); $$(4.3) -
(N3)
\(\mathbb{E}_{\mathbb{Q}^{\diamond }}[C^{\diamond }_{i}]=0\) for all \(i \in I\).
Remark 4.3
Suppose that the agents’ preferences and risk exposures are such that no trade occurs in an Arrow–Debreu equilibrium, which happens when all \(\mathbb{P}_{i}\) are the same (and equal to, say, ℙ); see Remark 2.5. In this case, \(\mathbb{Q}^{\ast }= \mathbb{P}\) and \(C^{\ast }_{i} = 0\) for all \(i \in I\). It is then straightforward from Theorem 4.2 to see that a Nash equilibrium is also given by \(\mathbb{Q}^{\diamond }= \mathbb{P}\) and \(C^{\diamond }_{i} = 0\) (and \(z^{\diamond }_{i} = 0\)) for all \(i \in I\). In fact, as argued in Sect. 4.3.4, this is the unique Nash equilibrium in this case. Conversely, suppose that a Nash equilibrium is given by \(\mathbb{Q}^{\diamond }= \mathbb{P}\) and \(C^{\diamond } _{i} = 0\) for all \(i \in I\). Then (4.3) shows that \(\mathbb{Q}^{\ast }= \mathbb{Q}^{\diamond }= \mathbb{P}\) and (4.2) implies that \(C^{\ast }_{i} \sim - z^{\diamond } _{i} \sim 0\), which means that \(C^{\ast }_{i} = 0\) for all \(i \in I\). In words, the Nash risk-sharing equilibrium involves no risk transfer if and only if the agents are already in a Pareto-optimal situation.
In the important case of two acting agents, since \(C^{\diamond }_{0} = - C^{\diamond }_{1}\), applying simple algebra in (4.2), we obtain that a Nash equilibrium risk-sharing security \(C^{\diamond } _{0}\) is such that \(-\delta_{1} < C^{\diamond }_{0} < \delta_{0}\) and satisfies
In Theorem 4.7, the existence of a unique Nash equilibrium for the two-agent case will be shown. Furthermore, a one-dimensional root-finding algorithm presented in Sect. 4.4 allows us to calculate the Nash equilibrium and further calculate and compare the final position of each individual agent. Consider, for instance, Example 3.8 and its symmetric situation illustrated in Fig. 2, where the limited liability of the security \(C^{\mathrm{r}}_{0}\) implies less variability and a flatter right tail for the agent’s position. Under the Nash equilibrium, as argued in Sect. 4.3.1, the security \(C^{\diamond }_{0}\) is further bounded from above, which implies that the probability density function of the agent’s final position is shifted to the left. This fact, in the setting of Example 3.8, is illustrated in Fig. 3.
The solid green line is the pdf of the position \(E_{0}+C^{\diamond }_{0}\), the dashed blue line illustrates the pdf of the position \(E_{0}+C^{\ast }_{0}\), and the dotted red line is the pdf of the position \(E_{0}+C^{\mathrm{r}}_{0}\), all under the common subjective probability measure. In this example, \(\sigma_{0}=\sigma _{1}=1\) and \(\rho =-0.5\)
Despite the above symmetric case, it is not necessarily true that all agents suffer a loss of utility at the Nash equilibrium risk sharing. As we shall see in Sect. 5, for agents with sufficiently large risk-tolerance, the negotiation game results in higher utility compared to the one gained through an Arrow–Debreu equilibrium.
4.3 Within equilibrium
According to Theorem 4.7, Nash equilibria in the sense of Definition 4.1 always exist. Throughout Sect. 4.3 , we assume that \((\mathbb{Q}^{\diamond }, (C^{\diamond }_{i})_{i \in I})\) is a Nash equilibrium and provide a discussion on certain of its aspects, based on the characterisation in Theorem 4.2.
4.3.1 Endogenous bounds on traded securities
As pointed out in Remark 3.4, the security that each agent enters resulting from the best response procedure is bounded below. When all participating agents follow the same strategic behaviour, Nash equilibrium securities are bounded from above as well. Indeed, since the market clears, the security that agents take a long position in is shorted by the rest of the agents, who similarly intend to bound their liabilities. Mathematically, since \(C^{\diamond }_{i} > - \delta_{-i}\) for all \(i \in I\) and \(\sum_{i \in I} C^{\diamond }_{i} = 0\), it also follows that \(C^{\diamond } _{i} = - \sum_{j \in I\setminus \left\{ i\right\} } C^{\diamond }_{j} < \sum_{j \in I\setminus \left\{ i\right\} } \delta_{-j} = (n -1) \delta + \delta_{i}\) for all \(i \in I\). Therefore, a consequence of the agents’ strategic behaviour is that Nash risk-sharing securities are endogenously bounded. This fact is in sharp contrast with the Arrow–Debreu equilibrium of (2.4), where the risk transfer may involve securities with unbounded payoffs. An immediate consequence of the bounds on the securities is that the potential gain from the Nash risk-sharing transaction is also endogenously bounded. Naturally, the resulting endogenous bounds are an indication of how the game among agents restricts the risk-sharing transaction, which in turn may be a source of a large loss of efficiency. The next example is an illustration of such an inefficiency in a simple symmetric setting. In Fig. 3, the loss of utility in the two-agent Example 3.8 is visualised.
Example 4.4
Let \(X \in \mathbb{L}^{0}\) have the standard (zero mean, unit standard deviation) Gaussian law under the baseline probability ℙ. For \(\beta \in \mathbf{R}\), define \(\mathbb{P}^{\beta }\in \mathcal{P}\) via \(\log (\mathrm{d}\mathbb{P}^{\beta }/ \mathrm{d}\mathbb{P})\sim \beta X\); under \(\mathbb{P}^{\beta }\), \(X\) has a Gaussian law with mean \(\beta \) and unit standard deviation. Fix \(\beta > 0\) and set \(\mathbb{P}_{0} \mathrel{\mathop{:}}=\mathbb{P}^{\beta }\) and \(\mathbb{P}_{1} \mathrel{\mathop{:}}=\mathbb{P}^{-\beta }\). In this case, it is straightforward to compute that \(C^{\ast }_{0} = \beta X = - C^{\ast }_{1}\). It also follows that \(u^{\ast }_{0} = \beta^{2} / 2 = u^{\ast }_{1}\). If \(\beta \) is large, then the discrepancy between the agents’ beliefs results in large monetary profits to both after the Arrow–Debreu transaction. On the other hand, as established in Theorem 4.7, in the case of two agents, there exists a unique Nash equilibrium. In fact, in this symmetric case, we have \(-1 < C^{\diamond }_{0} < 1\), and it can be checked that (see also (4.4) later)
The loss of efficiency caused by the game becomes greater with increasing values of \(\beta > 0\). In fact, if \(\beta \) converges to infinity, then it can be shown that \(C^{\diamond }_{0}\) converges to \(\mathrm{sign} (X) = \mathbb{I}_{\left\{ X > 0\right\} } - \mathbb{I} _{\left\{ X < 0\right\} }\); furthermore, both \(\mathbb{U}_{0} (C^{ \diamond }_{0})\) and \(\mathbb{U}_{1} (C^{\diamond }_{1})\) converge to 1, which demonstrates the tremendous inefficiency of the Nash equilibrium transaction compared to the Arrow–Debreu one.
Note that the endogenous bounds \(- \delta_{-i} < C^{\diamond }_{i} < (n -1) \delta + \delta_{i}\) depend only on the risk-tolerance profile of the agents and not on their actual beliefs (or risk exposures). In addition, these bounds become stricter in games where quite risk-averse agents are playing, as they become increasingly hesitant towards undertaking risk.
4.3.2 If trading, you never reveal your true beliefs
As discussed in Remark 3.3, agents’ best probability responses differ from their actual subjective beliefs in any situation where risk transfer is involved. This result becomes more pronounced when we consider the Nash risk-sharing equilibrium. To wit, if \((\mathbb{R}^{\diamond }_{i})_{i \in I}\) are revealed subjective beliefs corresponding to a Nash equilibrium, then it is a consequence of Theorem 4.2 (see also (3.4)) that
Note that \(\mathbb{R}^{\diamond }_{i} = \mathbb{P}_{i}\) if and only if \(C^{\diamond }_{i} = 0\) for any fixed \(i \in I\); therefore, whenever agents take part (by actually trading) in a Nash equilibrium, their reported subjective beliefs are never the same as their actual ones.
Even though in any nontrivial trading situation, agents report different subjective beliefs from their actual ones, we argue below that (4.5) imposes endogenous constraints on the magnitude of the possible discrepancy; the discussion that follows expands on Remark 3.1. Start by writing (4.5) as
and note that \(\mathbb{E}_{\mathbb{R}^{\diamond }_{i}} [C^{\diamond } _{i}] \geq - \delta_{i} \log \mathbb{E}_{\mathbb{R}^{\diamond }_{i}} [ \exp ( -C^{\diamond }_{i} / \delta_{i})] \geq 0\), where we have used Jensen’s inequality and the fact that \((\mathbb{Q}^{\diamond }, (C ^{\diamond }_{i})_{i \in I})\) is an Arrow–Debreu equilibrium for the fictitious agents’ preference pairs \((\delta_{i}, \mathbb{R}^{\diamond }_{i})_{i \in I}\). It follows that \(\kappa^{\diamond }_{i} \geq 0\), which implies that \(\mathrm{d}\mathbb{P}_{i} / \mathrm{d}\mathbb{R} ^{\diamond }_{i} \leq 1 + C^{\diamond }_{i} / \delta_{-i}\) for all \(i \in I\). Defining weights \((\alpha_{i})_{i \in I}\) as \(\alpha_{i} \mathrel{ \mathop{:}}=\delta_{-i}/n\delta = \lambda_{-i}/n\) for all \(i \in I\) (noting that \(0 < \alpha_{i} < 1/n\) for all \(i \in I\) and that \(\sum_{i \in I} \alpha_{i} = 1\)), the market clearing condition \(\sum_{i \in I}C^{\diamond }_{i} = 0\) gives \(\sum_{i \in I}\alpha_{i} (\mathrm{d}\mathbb{P}_{i} / \mathrm{d}\mathbb{R}^{\diamond }_{i}) \leq 1\). We can obtain a corresponding lower bound. Indeed, using the endogenous bounds \(C^{\diamond }_{i} \leq (n-1) \delta + \delta_{i}\), it follows that \(\kappa^{\diamond }_{i} \leq - \log \alpha_{i}\) for all \(i \in I\), which gives \(\mathrm{d}\mathbb{P}_{i} / \mathrm{d} \mathbb{R}^{\diamond }_{i} \geq \alpha_{i} (1 + C^{\diamond }_{i} / \delta_{-i}) = \alpha_{i} + C^{\diamond }_{i} / (n \delta )\). Using again the market clearing condition \(\sum_{i \in I}C^{\diamond }_{i} = 0\), it follows that \(\sum_{i \in I}(\mathrm{d}\mathbb{P}_{i} / \mathrm{d}\mathbb{R}^{\diamond }_{i}) \geq 1\). To recapitulate,
which imposes considerable a priori restrictions on the likelihood ratios \(\mathrm{d}\mathbb{P}_{i} / \mathrm{d}\mathbb{R}^{\diamond } _{i}\) for all \(i \in I\). (For example, there are no events for which all agents will overstate or understate their likelihood compared to their actual subjective beliefs.) In particular, since \(1 / \alpha_{i} = n / \lambda_{-i}\), we obtain that
The above upper bound on the likelihood of \(\mathbb{P}_{i}\) with respect to \(\mathbb{R}^{\diamond }_{i}\) only depends on the number of remaining agents \(n\) and the relative risk-tolerance coefficient of the agents; it depends neither on the aggregate risk-tolerance level \(\delta \) nor on the actual subjective beliefs of other agents. Furthermore, note also that (4.6) implies that \(\mathcal{H}( \mathbb{P}_{i} \, | \,\mathbb{R}^{\diamond }_{i}) = \mathbb{E}_{ \mathbb{P}_{i}} [\log (\mathrm{d}\mathbb{P}_{i} / \mathrm{d} \mathbb{R}^{\diamond }_{i})] \leq \log (n / \lambda_{-i})\). The latter gives an a priori endogenous estimate on the distance of the truth from the reported beliefs in a Nash equilibrium.
4.3.3 Loss of efficiency
As already mentioned, agents’ strategic behaviour results in risk-sharing inefficiency, which, since utilities \(( \mathbb{U}_{i})_{i \in I}\) are numerically represented by certainty equivalents, can be measured through the difference of the aggregate monetary utility under the Arrow–Debreu transaction and the aggregate monetary utility under the Nash equilibrium risk-sharing transaction. Note that similar measures of inefficiency have been used in the risk-sharing literature; see, for example, [30] or [2]. Mathematically, the loss of efficiency equals \(u^{\ast }- u^{\diamond }= \sum_{i \in I}u^{\ast }_{i} - \sum_{i \in I}u^{\diamond }_{i}\), where \((u^{\ast }_{i})_{i \in I}\) and \(u^{\ast }\) are defined in (2.5) and (2.6), whereas
From (2.7), (4.2) and (4.3) it follows that
Recalling that \(\mathbb{E}_{\mathbb{Q}^{\diamond }}[C^{\diamond }_{i}] = 0\) for all \(i \in I\) and noting the equality
which holds in view of (4.3), we obtain
Adding up (4.7) over \(i \in I\) and using the fact that \(\sum_{i \in I} z^{\diamond }_{i} = 0\), we obtain an analytic expression of the loss of efficiency caused by the game, namely,
Since \(\prod_{i \in I} (1 + C^{\diamond }_{i} / \delta_{-i})^{\lambda _{i}} \leq \sum_{i \in I} \lambda_{i} (1 + C^{\diamond }_{i} / \delta _{-i}) = 1 + \sum_{i \in I} \lambda_{i} C^{\diamond }_{i} / \delta _{-i}\) and \(\mathbb{E}_{\mathbb{Q}^{\diamond }}[C^{\diamond }_{i}] = 0\) for all \(i \in I\), we indeed have \(u^{\diamond }\leq u^{\ast }\) (which was anyway known from Remark 2.4); furthermore, \(u^{\diamond }= u^{\ast }\) if and only if \(C^{\diamond }_{i} = 0\) for all \(i\), which happens if and only if \(C^{\ast }_{i} = 0\) for all \(i\); see Remark 4.3. In other words, the Nash risk-sharing equilibrium always implies a strict loss of efficiency, except for the case where there is no trading within a Nash equilibrium (which is equivalent to the case where there is no trading within an Arrow–Debreu equilibrium as well).
4.3.4 A priori information on \(z^{\diamond }\)
From (4.7) and (4.8), we obtain
This gives an economic interpretation for the quantities \(z^{\diamond }_{i} = \lambda_{i} ( u^{\ast }- u^{\diamond }) + (u^{\diamond }_{i} - u^{\ast }_{i})\), \(i \in I\). Indeed, \(\lambda_{i} ( u^{\ast }- u^{ \diamond })\) is the fraction corresponding to agent \(i \in I\) of the aggregate loss of utility caused by forming a Nash instead of an Arrow–Debreu equilibrium; on the other hand, \(u^{\diamond }_{i} - u ^{\ast }_{i}\) is the difference between the utility that agent \(i \in I\) acquires in a Nash from the one in an Arrow–Debreu equilibrium.
Although the aggregate utility \(u^{\diamond }\) in Nash equilibrium risk sharing can never be higher than the Arrow–Debreu aggregate utility \(u^{\ast }\), it may happen that some agents benefit from the game in the sense that their individual utility after the negotiation game is higher when compared to the utility gain of the Arrow–Debreu equilibrium. We address such cases in Sect. 5.
Equation (4.9) is useful in obtaining tight bounds on \(z^{\diamond }= (z^{\diamond }_{i})_{i \in I}\). Since \(u^{\diamond } _{i} \geq 0\) for all \(i \in I\) and \(u^{\diamond }\leq u^{\ast }\), from (4.9) it follows that
Combined with \(\sum_{i \in I} z^{\diamond }_{i} = 0\), the previous a priori bounds imply that \(z^{\diamond }\) has to live in a compact simplex on \(\Delta^{I}\). The bounds in (4.10) are indeed sharp: in the no-trade setting of Remark 4.3, it follows that \(u^{\ast }_{i} = 0\) for all \(i \in I\), which implies that \(z^{\diamond }_{i} \geq 0\) for all \(i \in I\); since \(z^{\diamond } \in \Delta^{I}\), it follows that \(z^{\diamond }_{i} = 0\) for all \(i \in I\). This also shows that the trivial Nash equilibrium obtained in Remark 4.3 is unique.
4.3.5 Individual marginal indifference valuation
In view of (4.8) and the subsequent discussion, recalling Remark 2.4, it follows that the allocation in a Nash equilibrium fails to be Pareto-optimal (except in the trivial no-trade case). Another way to demonstrate the inefficiency of a Nash equilibrium is through the disagreement between the individual agent’s marginal (utility) indifference valuation measures after the Nash risk-sharing transaction.
Recall that given a position \(G_{i} \in \mathbb{L}^{0}\) with \(\mathbb{U}_{i}(G_{i}) > - \infty \), the marginal indifference valuation measure \(\mathbb{Q}_{i} = \mathbb{Q}_{i}(G_{i})\) of agent \(i \in I\) has the property that the function \(\mathbf{R}\ni q \mapsto \mathbb{U}_{i} (G_{i} + q (X - \mathbb{E}_{\mathbb{Q}_{i}} \left[ X\right] ) )\) is maximised at \(q = 0\) for all \(X \in \mathbb{L} ^{\infty }\); in other words, if prices are given by expectations under \(\mathbb{Q}_{i}\), agent \(i \in I\) has no incentive to take any position other than \(G_{i}\). Using the first-order conditions, it is straightforward to show that \(\log \left( \mathrm{d}\mathbb{Q}_{i} / \mathrm{d}\mathbb{P}_{i}\right) \sim - G_{i} / \delta_{i}\).
In an Arrow–Debreu equilibrium, the collection \((\mathbb{Q}^{\ast } _{i})_{i \in I} \in \mathcal{P}^{I}\) with the property \(\log ( \mathrm{d}\mathbb{Q}^{\ast }_{i} / \mathrm{d}\mathbb{P}_{i}) \sim - C ^{\ast }_{i} / \delta_{i}\) for \(i \in I\), which are the individual marginal indifference valuation measures associated with positions \((C^{\ast }_{i})_{i \in I}\) after the Arrow–Debreu risk-sharing transaction, satisfies \(\mathbb{Q}^{\ast }_{i} = \mathbb{Q}^{\ast }\) for all \(i \in I\): all agents’ marginal indifference valuation measures agree. Now denote the individual agent’s marginal indifference valuation measures after the Nash risk-sharing transaction by \((\mathbb{Q}^{ \diamond }_{i})_{i \in I}\), for which we have \(\log (\mathrm{d} \mathbb{Q}^{\diamond }_{i} / \mathrm{d}\mathbb{P}_{i}) \sim - C^{ \diamond }_{i} / \delta_{i}\) for all \(i \in I\). In view of \(\log \left( \mathrm{d}\mathbb{P}_{i} /\mathrm{d}\mathbb{Q}^{\ast }\right) \sim C^{\ast }_{i} / \delta_{i}\), (4.2) and (4.3), it follows that \(\log (\mathrm{d}\mathbb{Q}^{ \diamond }_{i} / \mathrm{d}\mathbb{Q}^{\diamond }) \sim \log (1 + C ^{\diamond }_{i} / \delta_{-i})\). Since \(\mathbb{E}_{ \mathbb{Q}^{\diamond }} [1 + C^{\diamond }_{i} / \delta_{-i}] = 1\), it follows that
Pareto optimality would require all \((\mathbb{Q}^{\diamond }_{i})_{i \in I}\) to agree, which is possible only if \(C^{\diamond }_{i} = 0\) for all \(i \in I\), that is, exactly when no trade occurs.
All Nash securities \((C^{\diamond }_{i})_{i \in I}\) have zero value under \(\mathbb{Q}^{\diamond }\). For each individual agent \(i \in I\), we can measure the marginal indifference value of \(C^{\diamond }_{i}\) via
In particular, note that \(\mathbb{E}_{\mathbb{Q}^{\diamond }_{i}} [C ^{\diamond }_{i}] \geq 0\), with strict inequality if \(C^{\diamond } _{i}\) is non-zero, for all \(i \in I\). This observation implies that (except in trivial situations of no trading) all agents would be better off if they would take a larger position in their individual securities; for all \(a \in \mathbf{R}_{+}\), the collection \((a C^{ \diamond }_{i})_{i \in I}\) of securities clears the market, and for some \(a > 1\), this collection of securities would result in higher utility for each agent than using the securities \((C^{\diamond }_{i})_{i \in I}\). Of course, what prevents agents from doing so is that they would find themselves in a (Nash) disequilibrium. The fact that agents will not agree on market-clearing collections \((a C^{\diamond }_{i})_{i \in I}\) that for some \(a > 1\) would be individually (and therefore, also collectively) preferable also indicates that trading volume within a Nash equilibrium tends to be reduced.
The individual marginal indifference valuation measures \((\mathbb{Q} ^{\diamond }_{i})_{i} \in I\) allow an interesting expression of the Nash valuation measure \(\mathbb{Q}^{\diamond }\). To wit, recall from Sect. 4.3.2 the weights \(\alpha_{i} = \delta_{-i}/n \delta \) for all \(i \in I\); then from (4.11) and the market clearing condition \(\sum_{i \in I} C_{i} = 0\), it follows that
In words, the Nash valuation measure \(\mathbb{Q}^{\diamond }\) is a convex combination of the individual agents’ marginal indifference valuation measures assigning weight \(\alpha_{i}\) to agent \(i \in I\). Note also that more risk-averse agents carry more weight; however, since \(\max_{i \in I} \alpha_{i} < 1/n\), \(\mathbb{Q}^{\diamond }\) is almost equal to the equally weighted average of \((\mathbb{Q}^{\diamond }_{i})_{i \in I}\) for large numbers of agents.
Relation (4.13) highlights the importance of risk-tolerance levels regarding the gain or loss of utility for individual agents in a Nash equilibrium. Consider, for instance, the situation of two interacting agents, with one of them being considerably more risk-tolerant than the other. In this case, \(\mathbb{Q}^{\diamond }\) will be very close to the risk-averse agent’s marginal utility-based valuation measure, which will agree with the quoted prices. On the other hand, the possible discrepancy of \(\mathbb{Q}^{\diamond }\) from the risk-tolerant agent’s marginal utility-based valuation is beneficial to this agent, as it gives the opportunity to purchase a positive-value security for zero price. A limiting instructive scenario along these lines is treated in Sect. 5.
The marginal indifference valuation measures \((\mathbb{Q}^{\diamond } _{i})_{i \in I}\) of (4.11) can be used to provide interesting formulas for the utility gain in a Nash equilibrium and the utility difference between the Nash and Arrow–Debreu transactions. Note first that (4.3) and (4.8) give
which, combined with (4.9) and the fact that \(C^{\ast }_{i} = \delta_{i} \log \left( \mathrm{d}\mathbb{P}_{i} / \mathrm{d}\mathbb{Q}^{\ast }\right) + u^{\ast }_{i}\), implies that
Using further (4.11) and taking expectation with respect to \(\mathbb{Q}^{\diamond }\) in (4.14), we obtain
The last equality has to be compared with (2.5). As in an Arrow–Debreu equilibrium, agents in a Nash equilibrium benefit from the distance of the resulting valuation measure from their subjective views; however, unlike the Pareto-optimal efficiency of the Arrow–Debreu transaction, agents in the Nash transaction suffer a loss from the distance of the valuation measure from their respective marginal indifference valuation measures.
From (4.14) and (4.11), it follows that \(C^{\diamond }_{i} = - \delta_{i} \log (\mathrm{d}\mathbb{Q}^{\diamond }_{i} / \mathrm{d} \mathbb{P}_{i}) + \mathbb{U}_{i}( C_{i})\); combining this with the fact that \(C^{\ast }_{i} = \delta_{i} \log (\mathrm{d}\mathbb{P}_{i} / \mathrm{d}\mathbb{Q}^{\ast }) + u^{\ast }_{i}\), we obtain the equality \(C^{\diamond }_{i} + \delta_{i} \log (\mathrm{d}\mathbb{Q}^{\diamond }_{i} / \mathrm{d}\mathbb{Q}^{\ast }) = C^{\ast }_{i} + (u^{\diamond }_{i} - u^{\ast }_{i})\) for all \(i \in I\). Taking expectations with respect to \(\mathbb{Q}^{\ast }\), it follows that
The difference of individual agents’ utilities in the two equilibria comes from two distinct sources. The first stems from the discrepancy (measured via the relative entropy) of the Arrow–Debreu valuation from the individual marginal indifference valuation of agent \(i \in I\) in a Nash equilibrium. When the agent’s marginal indifference valuation measure in a Nash equilibrium is close to the Arrow–Debreu measure, his loss of utility caused by the Nash game is lower. In a sense, this is the part of aggregate loss of utility that is “paid” by agent \(i \in I\) (see also (4.16) below). The other term on the right-hand side of (4.15) regards the price under the Arrow–Debreu valuation measure \(\mathbb{Q}^{\ast }\) of the actual security that agent \(i \in I\) buys at a Nash equilibrium. Recalling that Nash equilibrium prices of the Nash securities \((C^{\diamond }_{i})_{i \in I}\) are zero, positivity of \(\mathbb{E} _{\mathbb{Q}^{\ast }} [C^{\diamond }_{i}]\) implies that the security \(C^{\diamond }_{i}\) is undervalued in a Nash equilibrium transaction. Again, note that if \(\mathbb{Q}^{\diamond }_{i}\) is close to \(\mathbb{Q}^{\ast }\), then the valuation \(\mathbb{E}_{\mathbb{Q} ^{\ast }} [C^{\diamond }_{i}]\) tends to be positive since \(\mathbb{E} _{\mathbb{Q}^{\diamond }_{i}} [C^{\diamond }_{i}]\) is always nonnegative (see (4.12)). To recapitulate the previous discussion: agents whose marginal indifference valuation measure is close to the Arrow–Debreu one tend to benefit from the Nash game. As we shall see in Sect. 5, this happens, for example, when agent \(i \in I\) is sufficiently risk-tolerant.
Due to the market clearing condition \(\sum_{i \in I}C^{\diamond }_{i}=0\), the aggregate loss takes into account only the aggregate discrepancy of individual marginal measures from the Arrow–Debreu optimal one: under-valuation of certain securities is balanced by over-valuation of others. Indeed, adding up (4.15) over all \(i \in I\) gives
which measures Nash inefficiency as aggregate discrepancy from optimal valuation of the individual agents’ marginal indifference valuation in a Nash equilibrium. Equation (4.16) is the counterpart of (2.6), where the inefficiency of complete absence of trading as compared to Arrow–Debreu risk sharing is considered.
4.4 Existence and uniqueness of Nash equilibrium via finite-dimensional root finding
Theorem 4.2 is used as a guide in order to search for an equilibrium, parameterising candidates for optimal securities using the \(n\)-dimensional space \(\Delta^{I}\) introduced in (4.1). Proposition 4.5 that follows, and whose proof is the content of Sect. A.5, enables us to reduce the search of a Nash equilibrium, an inherently infinite-dimensional problem in our setting, to a finite-dimensional one. The latter problem gives the necessary tools for numerical approximations of Nash equilibria (see also Example 4.8).
Proposition 4.5
For all \(z \in \Delta^{I}\), there exists a unique \((C_{i}(z))_{i \in I} \in (\mathbb{L}^{0})^{I}\) with \(C_{i}(z) > - \delta _{-i}\) and
(Note that necessarily, \(\sum_{i \in I} C_{i}(z) = 0\) for all \(z \in \Delta^{I}\).) Furthermore,
In the notation of Proposition 4.5, for each \(z \in \Delta^{I}\), define the probability \(\mathbb{Q}(z)\) via
The uniform bounds \(- \delta_{-i} < C_{i}(z) < (n-1) \delta + \delta _{i}\) follow as in Sect. 4.3.1 and imply \(\exp ( C_{i}(z) / \delta_{i}) \in \mathbb{L}^{1}(\mathbb{Q}(z))\) for all \(i \in I\) and \(z \in \Delta^{I}\). In particular, \(\left( C_{i}(z)\right) _{i \in I} \in \mathcal{C}_{\mathbb{Q}(z)}\) for all \(z \in \Delta^{I}\). In view of Theorem 4.2, Nash equilibria amount to finding \(z \in \Delta^{I}\) such that \(\mathbb{E}_{\mathbb{Q}(z)}\left[ C_{i}(z)\right] = 0\) for all \(i \in I\). We can in fact define a function \(\ell : \Delta^{I}\to \mathbf{R}_{+}\) that gives a “distance from equilibrium” by the formula
Since \(C_{i}(z) > - \delta_{-i}\) for all \(z \in \Delta^{I}\), \(\ell \) is well defined. Furthermore, the inequality \(\log x \leq x-1\), valid for \(x \in (0, \infty )\), gives
in view of the fact that \(\sum_{i \in I} C_{i}(z) = 0\) for all \(z \in \Delta^{I}\), which shows that \(\ell \) is indeed \(\mathbf{R} _{+}\)-valued. Furthermore, since \(\log x < x-1\) for \(x \in (0, \infty ) \setminus \left\{ 1\right\} \), it follows for any \(z \in \Delta^{I}\) that \(\ell (z) = 0\) is equivalent to \(\mathbb{E}_{\mathbb{Q}(z)}\left[ C _{i}(z)\right] = 0\) for all \(i \in I\).
The following result summarises the above discussion.
Proposition 4.6
With the previous notation, the following are true:
-
Assume that \((\mathbb{Q}^{\diamond }, (C^{\diamond }_{i})_{i \in I})\) is a Nash equilibrium, and let \(z^{\diamond }\equiv (z^{\diamond } _{i})_{i \in I} \in \Delta^{I}\) be as in (4.2). Then \(\ell (z^{\diamond }) = 0\).
-
Assume that there exists \(z^{\diamond } {\in} \Delta^{I}\) with \(\ell (z^{\diamond }) {=} 0\). Then the pair \((\mathbb{Q}(z^{\diamond }), (C_{i} (z^{\diamond }))_{i \in I})\) defined as in (4.17) and (4.19) is a Nash equilibrium.
Proposition 4.6 provides a one-to-one correspondence between Nash equilibria and roots of \(\ell \). Recalling the discussion in Sect. 4.3.4, any root of \(\ell \) belongs to the compact subset of \(\Delta^{I}\) consisting of \((z_{i})_{i \in I} \in \Delta^{I}\) with \(z_{i} \geq - u^{\ast }_{i}\) for all \(i\). This allows numerical approximations of Nash equilibria, for example, by Monte Carlo simulation.
Its practical usefulness notwithstanding, Proposition 4.6 does not answer the question of actual existence of Nash equilibria nor, in case of existence, the uniqueness. These issues are settled in Theorem 4.7, whose proof is the subject of Sect. A.6.
Theorem 4.7
A Nash risk-sharing equilibrium always exists. When we additionally have \(I = \left\{ 0,1\right\} \), a Nash risk-sharing equilibrium is necessarily unique.
The question of uniqueness for three or more agents remains open and is significantly more challenging from a mathematical perspective. In all cases of numerical simulation that were carried out, we observed the (existence and) uniqueness of a Nash equilibrium. The next example is representative.
Example 4.8
Consider a three-agent game with \(\delta_{0} = \delta_{1} = \delta _{2} = 1\). Here, we have \(\log (\mathrm{d}\mathbb{P}_{i} / \mathrm{d} \mathbb{P}) \sim X_{i}\) for \(i \in \left\{ 0,1,2\right\} \), where \((X_{0}, X_{1}, X_{2})\) under ℙ has a mean-zero normal distribution with \(\sigma (X_{0}) = 0.4\), \(\sigma (X_{1}) = 2.7\), \(\sigma (X_{2}) = 1.1\), \(\rho (X_{0}, X_{1})=-0.9\), \(\rho (X_{0},X_{2})=0.7\) and \(\rho (X_{1},X_{2})=-0.3\). In Fig. 4, we plot the function \(\ell \) for different values of \((z_{1}, z_{2})\) in the bounded region specified by the inequalities \(z_{1} \geq - u^{\ast }_{1}\), \(z_{2} \geq - u^{\ast }_{2}\) and \(z_{1} + z_{2} \leq u^{\ast }_{0}\), where we recall that \(z_{1} + z _{2} = - z_{0}\). As can be seen, there is a unique root of \(\ell \) approximately at the vector
The function \(\ell \) for different values of \(z\), corresponding to Example 4.8
5 Extreme risk-tolerance
As discussed in Sect. 4.3.5, risk-tolerance coefficients are crucial factors in the gain or loss caused by the game in each agent’s utility. In this section, we investigate this issue more closely by studying and comparing the Arrow–Debreu and Nash risk-sharing equilibria when agents’ risk preferences approach risk-neutrality in the sense that risk-tolerance approaches infinity. In order to focus on the economic interpretation of the results, we consider the simplified (but representative) case of two agents.
The analysis that follows examines two cases: firstly, when only one agent becomes extremely risk-tolerant, and secondly, when both agents’ risk-tolerance coefficients uniformly approach infinity. Besides the interest of this analysis in its own right, it also allows us to substantiate the claim that highly risk-tolerant agents are the ones who in fact benefit from the risk-sharing game.
5.1 One extremely risk-tolerant agent
We start with the two-agent case \(I = \left\{ 0,1\right\} \), where the risk-aversion of only one agent approaches zero. We keep the risk-tolerance \(\delta_{1}\) and subjective probability \(\mathbb{P} _{1}\) of agent 1 fixed. On the other hand, for agent 0, we consider a sequence of risk-tolerance coefficients \((\delta_{0}^{m})_{m \in \mathbf{N}}\) with \(\lim_{m \to \infty }\delta^{m}_{0} = \infty \) and a fixed subjective probability \(\mathbb{P}_{0}\). In this setup, Theorems 2.2 and 4.7 state that for each \(m \in \mathbf{N}\), there exist a unique Arrow–Debreu equilibrium \((\mathbb{Q}^{m, \ast }, (C^{m, \ast }_{i})_{i \in I})\) and a unique Nash equilibrium \((\mathbb{Q}^{m, \diamond }, (C^{m, \diamond }_{i})_{i \in I})\). We use agent 0 as the baseline and focus on the securities \(C^{m, \ast }_{0}\) and \(C^{m, \diamond }_{0}\) since \(C^{m, \ast }_{1} = -C^{m, \ast }_{0}\) and \(C^{m, \diamond }_{1} = -C^{m, \diamond } _{0}\).
We first examine the limiting behaviour of the valuation rule and the securities in the Arrow–Debreu equilibrium transaction. For each \(m \in \mathbf{N}\), we obtain from (2.3) that \(\mathbb{Q} ^{m, \ast }\in \mathcal{P}\) has \(\log (\mathrm{d}\mathbb{Q}^{m, \ast }/ \mathrm{d}\mathbb{P}_{0}) \sim \lambda_{1}^{m} \log ( \mathrm{d}\mathbb{P}_{1} / \mathrm{d}\mathbb{P}_{0})\). More precisely, we have
Given that \(\lim_{m \to \infty }\lambda_{1}^{m} = 0\), \(\mathbb{L}^{0} \mbox{-} \lim_{m \to \infty }\left( \mathrm{d}\mathbb{Q}^{m, \ast }/ \mathrm{d}\mathbb{P}_{0}\right) = 1\) readily follows from the dominated convergence theorem—in fact, with \(\left| \,\cdot \,\right| _{ \mathrm{TV}}\) denoting the total-variation norm, Scheffé’s lemma implies that \(\lim_{m \to \infty }\left| \mathbb{Q}^{m, \ast }- \mathbb{P}_{0}\right| _{\mathrm{TV}} = 0\). Since
for all \(m \in \mathbf{N}\) and \((\mathbb{Q}^{m, \ast })_{m \in \mathbf{N}}\) converges to \(\mathbb{P}_{0}\), we expect the limiting relationship \(\mathbb{L}^{0} \mbox{-} \lim_{m \to \infty }C^{m, \ast }_{0} = \delta_{1} \log (\mathrm{d}\mathbb{P}_{0} / \mathrm{d} \mathbb{P}_{1}) - \delta_{1} \mathcal{H}(\mathbb{P}_{0} \, | \, \mathbb{P}_{1})\). Clearly, for the previous limit to be valid, the following (technical) assumption is necessary.
Assumption 5.1
\(\mathcal{H}(\mathbb{P}_{0} \, | \,\mathbb{P}_{1}) < \infty \).
In Sect. A.7, it is shown that the latter assumption is also sufficient for the validity of Proposition 5.2, giving the limiting valuation and security in an Arrow–Debreu equilibrium and the limiting gains of both agents.
Proposition 5.2
Under Assumption 5.1, the following limiting relations hold:
\(\lim_{m \to \infty }u^{m, \ast }_{0} = 0\) and \(\lim_{m \to \infty }u ^{m, \ast }_{1} = \delta_{1} \mathcal{H}(\mathbb{P}_{0} \, | \, \mathbb{P}_{1})\).
It is indeed expected that the utility gain of a nearly risk-neutral agent is almost zero. To see this, compare the limiting valuation measure \(\mathbb{P}_{0}\) with the limiting utility of agent 0, which is the linear expectation with respect to \(\mathbb{P}_{0}\). On the other hand, the only case where there is no limiting utility gain for agent 1 is when the two agents’ subjective beliefs coincide.
We now turn to a Nash risk-sharing equilibrium. From (4.4), we obtain
Accepting that the sequence \((z^{m, \diamond }_{0})_{m \in \mathbf{N}}\) converges in \(\mathbf{R}\) and \((C^{m, \diamond }_{0})_{m \in \mathbf{N}}\) converges in \(\mathbb{L}^{0}\) (these conjectures actually have to be proved as part of Theorem 5.4 below), and given that \(\lim_{m \to \infty }\delta^{m}_{0} = \infty \), \(\lim_{m \to \infty }\lambda_{0} ^{m} = 1\) and \(\mathbb{L}^{0} \mbox{-} \lim_{m \to \infty }C^{m, \ast }_{0} = C^{\infty , \ast }_{0}\), the limiting security \(C^{\infty , \diamond }_{0} \mathrel{\mathop{:}}=\mathbb{L}^{0} \mbox{-} \lim_{m \to \infty }C^{m, \diamond }_{0}\) should satisfy
where we set \(z^{\infty , \diamond }_{0} \mathrel{\mathop{:}}= \lim_{m \to \infty }z^{m, \diamond }_{0}\). This heuristic discussion gives a method to compute the limit. For \(z \in \mathbf{R}\), define the random variable \(C^{\infty }_{0}(z)\) by the equation
Since the function \((- 1, \infty ) \ni x \mapsto x + \log \left( 1 + x\right) \) is strictly increasing and continuous and maps \((-1, \infty )\) to \((- \infty , \infty )\), it follows that \(C^{\infty }_{0}(z)\) is a well-defined \((- \delta_{1}, \infty )\)-valued random variable for all \(z \in \mathbf{R}\). So we should have \(C^{\infty , \diamond }_{0} = C^{\infty }_{0} (z^{\infty , \diamond }_{0})\). Although \(z^{\infty , \diamond }_{0}\) is given as the limit of \((z^{m, \diamond }_{0})_{m \in \mathbf{N}}\), we may actually identify a priori what its value will be. To make headway, note that from (4.3),
and the fact that \(\lim_{m \to \infty }\left| \mathbb{Q}^{m, \ast }- \mathbb{P}_{0}\right| _{\mathrm{TV}} = 0\), the limiting Nash valuation probability \(\mathbb{Q}^{\infty , \diamond }\) should have \(\log ( \mathrm{d}\mathbb{Q}^{\infty , \diamond }/ \mathrm{d}\mathbb{P}_{0}) \sim -\log (1 + C^{\infty , \diamond }_{0} / \delta_{1})\); since we expect \(\mathbb{E}_{\mathbb{Q}^{\infty , \diamond }} [C^{\infty , \diamond }_{0}] = 0\), we actually obtain that the equality \(\mathbb{E}_{\mathbb{P}_{0}} [ (1 + C^{\infty , \diamond }_{0} / \delta _{1})^{-1} ] = 1\) should be satisfied. The next result, whose proof is given in Sect. A.8, ensures that a unique such candidate \(z^{\infty , \diamond }_{0} \in \mathbf{R}\) exists.
Lemma 5.3
In the notation of (5.2), there exists a unique \(z^{\infty , \diamond }_{0} \in \mathbf{R}\) satisfying the equality \(\mathbb{E}_{\mathbb{P}_{0}} [ (1 + C^{\infty }_{0}(z^{\infty , \diamond }_{0}) / \delta_{1})^{-1} ] = 1\).
Before we state our main result on the limiting behaviour of a Nash equilibrium, we make a final observation. Note that in view of (4.5), for all \(m \in \mathbf{N}\), we have \(\log ( \mathrm{d}\mathbb{R}^{m, \diamond }_{1} / \mathrm{d} \mathbb{P}_{1}) \sim - \log (1 - C^{m, \diamond }_{0} / \delta^{m} _{0})\). Since \(\lim_{m \to \infty }\delta_{0}^{m} = \infty \) and, as it turns out, \((C^{m, \diamond }_{0})_{m \in \mathbf{N}}\) is convergent, the revealed subjective probability \(\mathbb{R}^{m, \diamond }_{1}\) of agent 1 when \(m\) is large is close to the actual \(\mathbb{P}_{1}\). (There is an alternative way to obtain the same intuition. From (4.6), note that \(\mathrm{d}\mathbb{R}^{m, \diamond }_{1} / \mathrm{d}\mathbb{P}_{1} \geq \lambda_{0}^{m}\) for all \(m \in \mathbf{N}\). Since \(\lim_{m \to \infty }\lambda_{0}^{m} = 1\) and \((\mathrm{d}\mathbb{R}^{m, \diamond }_{1} / \mathrm{d}\mathbb{P}_{1})_{m \in \mathbf{N}}\) has constant expectation 1 under \(\mathbb{P}_{1}\), \((\mathbb{R}^{m, \diamond }_{1})_{m \in \mathbf{N}}\) must converge to \(\mathbb{P}_{1}\).) This suggests the same asymptotic behaviour as in the case discussed in Sect. 3.3, where only agent 0 acts strategically as indicated by the best probability response, whereas agent 1 reports true subjective beliefs \(\mathbb{P}_{1}\). Indeed, the following result, whose proof is given in Sect. A.9, implies that the limiting security structure is the same, regardless of whether the risk-averse agent 1 enters the game or simply reports true subjective beliefs (in which case only the approximately risk-neutral agent behaves strategically).
Theorem 5.4
With the previous notation (in particular, of Lemma 5.3), we have
The equality of the limits of \((C^{m, \diamond }_{0})_{m \in \mathbf{N}}\) and \((C_{0}^{m,\mathrm{r}})_{m \in \mathbf{N}}\) implies that the strategic behaviour of a risk-neutral agent dominates the risk-sharing transaction. Intuitively, agents with high risk-tolerance are willing to undertake more risk at the sharing transaction in return for a higher cash compensation. Thus, at the limit, the risk-neutral agent satisfies the reported hedging needs of other agents but achieves better prices by applying the best response strategy. On the other hand, for the risk-averse agent, the risk reduction is more important than a higher price to be paid. As a result, at equilibrium, the risk-averse agent prefers to submit true beliefs even though this results in a higher price to be paid to the risk-neutral agent. The situation is totally different in an Arrow–Debreu equilibrium transaction, where agents act basically as price takers and the securities and prices are determined by the efficiency of the transaction.
We argued in Sect. 4.3 that in any risk-transfer situation, the Nash equilibrium incurs some loss of efficiency. Although the aggregate utility is reduced in a Nash equilibrium when compared with the Arrow–Debreu one, certain agents may obtain a higher utility gain in risk-sharing games. In particular, Proposition 5.5 (whose proof is given in Sect. A.10) demonstrates that an agent with sufficiently high risk-tolerance enjoys a higher utility at a Nash equilibrium transaction than the utility at the Arrow–Debreu equilibrium sharing.
Proposition 5.5
Define \(\mathbb{Q}^{\infty , \diamond }\in \mathcal{P}\) with \(\mathrm{d}\mathbb{Q}^{\infty , \diamond }/ \mathrm{d}\mathbb{P}_{0} = (1 + C^{\infty , \diamond }_{0} / \delta_{1})^{-1}\). Then:
The limiting loss for the risk-averse agent comes from two sides. The first is \((1 / \delta_{1}) \mathrm{Var}_{\mathbb{Q}^{\infty , \diamond }} (C^{\infty , \diamond }_{0})\), which is the limiting gain of agent 0. The remaining quantity \(\delta_{1} \mathcal{H}( \mathbb{Q}^{ \infty , \ast }| \mathbb{Q}^{\infty , \diamond })\) is in fact the loss from the applied strategic behaviour as opposed to sharing in a Pareto-optimal way. Both terms are strictly positive as long as \(C^{\infty , \diamond }_{0}\) is not identically equal to zero.
The message of Proposition 5.5 is clear. The introduction of strategic behaviour allows agents with high risk-tolerance to achieve better prices that the more risk-averse agents are willing to pay in order to achieve risk reduction. In contrast to the Arrow–Debreu equilibrium where prices are given by the optimal sharing measure, agents with sufficiently high risk-tolerance are willing to accept more risk in the Nash game since their strategy drives the market to better cash compensation for them. In fact, a more risk-averse agent not only tends to undertake all the efficiency loss caused by the game, but also fuels the utility gain of the (sufficiently) risk-tolerant counterparty.
Recalling the discussion and notation of Sect. 4.3.5, we may offer some more detailed comments. From (4.11) and Proposition 5.5, it follows that the marginal valuation measure of agent 0 approaches the limiting optimal valuation measure \(\mathbb{Q}^{\infty , \ast }\). In turn, this implies that for large enough \(m \in \mathbf{N}\), the security that agent 0 gets in a Nash equilibrium is undervalued—indeed, note that
According to (4.15) and the discussion that follows, we readily get that the utility of agent 0 is increased. For the risk-averse agent, the situation is different. From (4.13), it follows that \(\mathbb{Q}^{m, \diamond }_{1}\) is close to \(\mathbb{Q}^{m, \diamond }\) for large \(m \in \mathbf{N}\), which in turn is close to \(\mathbb{Q}^{\infty , \diamond }\). Hence, for large enough \(m \in \mathbf{N}\), the security received by agent 1 in a Nash equilibrium is overvalued; on top of this, agent 1 also carries all the risk-sharing inefficiency of a Nash equilibrium.
5.2 Both agents being extremely risk-tolerant
We have seen before that the strategic behaviour of a highly risk-tolerant agent dominates the Nash game and drives the market to his preferred transaction, regardless of the actions of the other agent. Here, we examine what happens to the equilibria when both agents approach risk-neutrality at the same speed. More precisely, we fix \(\lambda_{0} \in (0,1)\) and \(\lambda_{1} \in (0,1)\) with \(\lambda_{0} + \lambda_{1} = 1\) and consider a nondecreasing sequence \(\left( \delta ^{m}\right) _{m \in \mathbf{N}}\) with \(\lim_{m \to \infty }\delta^{m} = \infty \). Define \(\delta^{m}_{i} \mathrel{\mathop{:}}=\lambda_{i} \delta^{m}\) for all \(m \in \mathbf{N}\) and \(i \in \left\{ 0,1\right\} \). In contrast to the setup of Sect. 5.1, here the subjective beliefs of the agents have to depend on \(m \in \mathbf{N}\). To obtain intuition on why and how the subjective probabilities must behave, note that according to Theorem 2.2, the security \(C^{m, \ast }_{0}\) is for all \(m \in \mathbf{N}\) given as a multiple by \(\delta_{0}^{m}\) of a random variable whose dependence on risk-tolerance comes only through \(\lambda_{0}\) and \(\lambda_{1}\). Since the latter weights are fixed for each \(m \in \mathbf{N}\), to guarantee that the securities in an Arrow–Debreu equilibrium have a well-behaved limit, we make the following assumption.
Assumption 5.6
For \(i \in \left\{ 0,1\right\} \), there exists \(\xi_{i} \in \mathbb{L} ^{\infty }\) such that \(\mathbb{E}_{\mathbb{P}}\left[ \xi_{i}\right] = 0\) and
Note that the condition \(\mathbb{E}_{\mathbb{P}}\left[ \xi_{i}\right] = 0\) for \(i \in \left\{ 0,1\right\} \) appearing in Assumption 5.6 is just a normalisation and does not constitute any loss of generality.
Theorem 5.7
In the above setup and under Assumption 5.6, the two sequences \((C^{m, \ast }_{0})_{m \in \mathbf{N}}\) and \((C^{m, \diamond }_{0})_{m \in \mathbf{N}}\) converge in \(\mathbb{L}^{0}\) to limiting securities \(C^{\infty , \ast }_{0}\) and \(C^{\infty , \diamond }_{0}\), where
The proof of Theorem 5.7 is given in Sect. A.11. Interestingly, the risk-neutrality of both agents drives the Nash equilibrium to half of the Arrow–Debreu securities, which is evidence of the market inefficiency caused by the strategic behaviour of risk-neutral agents. The result of Theorem 5.7 is another manifestation of the claim (initially made in Sect. 4.3.5) that the trading volume in a Nash equilibrium tends to be lower than the Pareto-optimal allocations.
References
Acciaio, B.: Optimal risk sharing with non-monotone monetary functionals. Finance Stoch. 11, 267–289 (2007)
Acharya, V., Bisin, A.: Optimal financial-market integration and security design. J. Bus. 78, 2397–2434 (2005)
Allen, F., Gale, D.: Arbitrage, short sales and financial innovation. Econometrica 59, 1041–1068 (1991)
Allen, F., Gale, D.: Financial Innovation and Risk Sharing. MIT Press, Cambridge (1994)
Arrow, K.: Uncertainty and the welfare of medical care. Am. Econ. Rev. 53, 941–973 (1963)
Axelson, U.: Security design with investor private information. J. Finance 62, 2587–2632 (2007)
Barrieu, P., El Karoui, N.: Inf-convolution of risk measures and optimal risk transfer. Finance Stoch. 9, 269–298 (2005)
Billot, A., Chateauneuf, A., Gilboa, I., Tallon, J.-M.: Sharing beliefs: between agreeing and disagreeing. Econometrica 68, 685–694 (2000)
Bisin, A.: General equilibrium with endogenously incomplete financial markets. J. Econ. Theory 82, 19–45 (1998)
Borch, K.: Equilibrium in a reinsurance market. Econometrica 30, 424–444 (1962)
Braido, L.: General equilibrium with endogenous securities and moral hazard. Econ. Theory 26, 85–101 (2005)
Bühlmann, H.: The general economic principle premium. ASTIN Bull. 14, 13–21 (1984)
Bühlmann, H., Jewell, S.: Optimal risk exchanges. ASTIN Bull. 10, 243–262 (1979)
Carvajal, A., Rostek, M., Weretka, M.: Competition in financial innovation. Econometrica 80, 1895–1936 (2012)
Duffie, D., Jackson, M.: Optimal innovation of futures contracts. Rev. Financ. Stud. 2, 275–296 (1989)
Filipović, D., Svindland, G.: Optimal capital and risk allocations for law- and cash-invariant convex functions. Finance Stoch. 12, 423–439 (2008)
Finnerty, J.: An overview of corporate security innovation. J. Appl. Corp. Finance 4, 23–39 (1992)
Föllmer, H., Scheid, A.: Stochastic Finance, 2nd edn. de Gruyter, Berlin (2004)
Jouini, E., Schachermayer, W., Touzi, N.: Optimal risk sharing for law invariant monetary utility functions. Math. Finance 18, 269–292 (2008)
Kyle, A.: Informed speculation with imperfect competition. Rev. Econ. Stud. 56, 317–355 (1989)
Marin, J., Rahi, R.: Information revelation and market incompleteness. Rev. Econ. Stud. 67, 563–579 (2000)
Nachman, D., Noe, T.: Optimal design of securities under asymmetric information. Rev. Financ. Stud. 7, 1–44 (1994)
Park, I.: Moral hazard contracting and private credit markets. Econometrica 72, 701–746 (2004)
Rahi, R., Zigrand, J.-P.: Strategic financial innovation in segmented markets. Rev. Financ. Stud. 22, 2941–2971 (2009)
Rostek, M., Weretka, M.: Dynamic thin markets. Rev. Financ. Stud. 28, 2946–2992 (2015)
Scheinkman, J., Xiong, W.: Heterogeneous beliefs, speculation and trading in financial markets. In: Carmona, R., et al. (eds.) Paris–Princeton Lectures on Mathematical Finance. Lecture Notes in Mathematics, vol. 1847, pp. 217–250. Springer, Berlin (2003)
Tufano, P.: Financial innovation. In: Constantinidis, G., et al. (eds.) Handbook of the Economics of Finance (Volume 1a: Corporate Finance), pp. 307–336. Elsevier/North-Holland, Amsterdam (2003)
Varian, H.: Divergence of opinion in complete markets: a note. J. Finance 40, 309–317 (1985)
Varian, H.: Differences of opinion in financial markets. In: Stone, C.C. (ed.) Financial Risk: Theory, Evidence, and Implications, Proceedings of the Eleventh Annual Economic Policy Conference of the Federal Reserve Bank of St. Louis, pp. 3–37. Kluwer Academic, Boston (1989)
Vayanos, D.: Strategic trading and welfare in a dynamic market. Rev. Econ. Stud. 66, 219–254 (1999)
Williams, N.: Persistent private information. Econometrica 79, 1233–1275 (2011)
Author information
Authors and Affiliations
Corresponding author
Additional information
M. Anthropelos acknowledges support from the Research Center of the University of Piraeus. C. Kardaras acknowledges support from the MC grant FP7-PEOPLE-2012-CIG, 334540.
Appendix: Proofs
Appendix: Proofs
1.1 A.1 Proof of Theorem 2.2
Suppose that \((\mathbb{Q}^{\ast }, (C^{\ast }_{i})_{i \in I})\) is an Arrow–Debreu equilibrium. We show the necessity of (2.3) and (2.4). For all \(i \in I\), note that \(\mathbb{U}_{i} (C ^{\ast }_{i}) \geq \mathbb{U}_{i} (0) = 0\), which implies that \(\exp (- C^{\ast }_{i} / \delta_{i}) \in \mathbb{L}^{1}(\mathbb{P} _{i})\). Fix \(X \in \mathbb{L}^{\infty }\) with \(\mathbb{E}_{\mathbb{Q} ^{\ast }}[X] = 0\) and \(i \in I\). Since the function \(\mathbf{R}\ni \epsilon \mapsto \mathbb{U}_{i}(C^{\ast }_{i} + \epsilon X) \in \mathbf{R}\) has a maximum at \(\epsilon = 0\), the first-order conditions and the dominated convergence theorem, using the fact that \(\exp (- C ^{\ast }_{i} / \delta_{i}) \in \mathbb{L}^{1}(\mathbb{P}_{i})\), imply that \(\mathbb{E}_{\mathbb{P}_{i}} [\exp (-C^{\ast }_{i} / \delta_{i}) X ] = 0\). The latter equality holds for all \(X \in \mathbb{L}^{\infty }\) with \(\mathbb{E}_{\mathbb{Q}^{\ast }} [X] = 0\) and all \(i \in I\); therefore, \(C^{\ast }_{i} \sim \delta_{i} \log (\mathrm{d}\mathbb{P} _{i} / \mathrm{d}\mathbb{Q}^{\ast })\) for all \(i \in I\). Since \(\mathbb{E}_{\mathbb{Q}^{\ast }} [C^{\ast }_{i}] = 0\), (2.4) follows. Furthermore, \(\sum_{i \in I}C^{\ast } _{i} = 0\) gives \(\sum_{i \in I}\delta_{i} \log (\mathrm{d}\mathbb{P} _{i} / \mathrm{d}\mathbb{Q}^{\ast }) \sim 0\), from which (2.3) follows.
Assume now that \((\mathbb{Q}^{\ast }, (C^{\ast }_{i})_{i \in I})\) is given by (2.3) and (2.4). By definition, \(\mathbb{E}_{\mathbb{Q}^{\ast }} [C^{\ast }_{i}] = 0\) for all \(i \in I\). Furthermore, (2.3) and (2.4) give
Together with \(\mathbb{E}_{\mathbb{Q}^{\ast }} [C^{\ast }_{i}] = 0\) for all \(i \in I\), this implies \(\sum_{i \in I}C^{\ast }_{i} = 0\). The fact that \(C^{\ast }_{i}\) is optimal for agent \(i \in I\) under the valuation measure \(\mathbb{Q}^{\ast }\) is argued in Remark 2.4. We have shown that \((\mathbb{Q}^{\ast }, (C^{\ast }_{i})_{i \in I})\) given by (2.3) and (2.4) is an Arrow–Debreu equilibrium. The necessity of (2.3) and (2.4) for an Arrow–Debreu equilibrium proved in the previous paragraph establishes its uniqueness. □
1.2 A.2 Proof of Proposition 3.2
To ease the reading, in the course of the proof of Proposition 3.2, we denote \(\mathbb{Q}^{( \mathbb{R}_{-i},\mathbb{R}^{\mathrm{r}}_{i})}\) by \(\mathbb{Q}_{i}^{ \mathrm{r}}\).
1.2.1 A.2.1 First-order conditions
We prove here the necessity of the stated conditions for a best response. Fix \(i \in I\) and \(\mathbb{R}^{\mathrm{r}}_{i} \in \mathcal{P}\) such that \(\mathbb{V}_{i} (\mathbb{R}^{\mathrm{r}}_{i}; \mathbb{R}_{-i}) = \sup_{\mathbb{R}_{i} \in \mathcal{P}} \mathbb{V} _{i} (\mathbb{R}_{i};\mathbb{R}_{-i})\). For \(\mathbb{R}^{0}_{i} \in \mathcal{P}\) defined via \(\log \mathrm{d}\mathbb{R}^{0}_{i} \sim (1 / \lambda_{-i}) \sum_{j \in I\setminus \left\{ i\right\} } \lambda_{j} \log \mathrm{d}\mathbb{R}_{j}\), it is straightforward to check that the resulting contract for agent \(i \in I\) would be zero; therefore,
In particular, we have \(\exp (- C^{\mathrm{r}}_{i} / \delta_{i}) \in \mathbb{L}^{1}(\mathbb{P}_{i})\), a fact that will be useful in several places for applying the dominated convergence theorem in the sequel.
Fix \(X \in \mathbb{L}^{\infty }\). For any \(\epsilon \in \mathbf{R}\), let \(\mathbb{R}_{i} (\epsilon ) \in \mathcal{P}\) be defined via the recipe
Letting \(\mathbb{Q}(\epsilon ) := \mathbb{Q}^{(\mathbb{R}_{-i}, \mathbb{R}_{i} (\epsilon ))}\) for \(\epsilon \in \mathbf{R}\), \(\log (\mathrm{d}\mathbb{Q}(\epsilon ) / \mathrm{d}\mathbb{Q}_{i}^{ \mathrm{r}}) \sim - \epsilon X / \delta_{-i}\) follows. In accordance with \(C^{\mathrm{r}}_{i}\), for \(\epsilon \! \in \! \mathbf{R}\), define \(C_{i}(\epsilon ) {=} \delta_{i} \log (\mathrm{d}\mathbb{R}_{i} (\epsilon ) / \mathrm{d}\mathbb{Q}(\epsilon )) {+} \delta_{i} \mathcal{H}( \mathbb{Q}(\epsilon ) \, | \,\mathbb{R}_{i} (\epsilon ))\) and then \(C_{i}(0) = C^{\mathrm{r}}_{i}\). Noting that
it follows that \(C_{i}(\epsilon ) = C^{\mathrm{r}}_{i} - \epsilon X - \mathbb{E}_{\mathbb{Q}(\epsilon )} [C^{\mathrm{r}}_{i} - \epsilon X]\), where the constant in the equivalence was cancelled by the definition of \(C_{i}(\epsilon )\). The dominated convergence theorem and simple differentiation, using also that \(\mathbb{E}_{\mathbb{Q}_{i}^{ \mathrm{r}}} [C^{\mathrm{r}}_{i}] = 0\), imply that
Since \(\mathbb{V}_{i}(\mathbb{R}(\epsilon ); \mathbb{R}_{-i}) = \mathbb{U}_{i} (C_{i}(\epsilon ))\) for all \(\epsilon \in \mathbf{R}\), another application of the dominated convergence theorem gives
Since \(\mathbf{R}\ni \epsilon \mapsto \mathbb{V}_{i}(\mathbb{R}( \epsilon ) ; \mathbb{R}_{-i})\) is maximised at \(\epsilon = 0\), the first-order conditions give
Noting that \(\sum_{j \in I\setminus \left\{ i\right\} } \lambda_{j} \log ( \mathrm{d}\mathbb{R}_{j} / \mathrm{d}\mathbb{P}_{i}) \sim \log ( \mathrm{d}\mathbb{Q}_{i}^{\mathrm{r}}/ \mathrm{d}\mathbb{P} _{i}) - \lambda_{i} \log ( \mathrm{d}\mathbb{R}^{\mathrm{r}}_{i} / \mathrm{d}\mathbb{P}_{i})\) implies
it follows from \(C^{\mathrm{r}}_{i} \sim \delta_{i} \log ( \mathrm{d} \mathbb{R}^{\mathrm{r}}_{i} / \mathrm{d}\mathbb{Q}_{i}^{\mathrm{r}})\) that
The last equivalence relation allows us to write (A.1) as
where
Up to now, \(X \in \mathbb{L}^{\infty }\) was fixed but arbitrary. Varying \(X\) over \(\mathbb{L}^{\infty }\) in (A.2) gives
Necessarily, \(C^{\mathrm{r}}_{i} > - \delta_{-i}\) should hold. Taking logarithms and rearranging (A.4) gives (3.2).
1.2.2 A.2.2 Optimality of candidates for best response
We now proceed to showing that the necessary conditions for a best response are also sufficient. (As mentioned in the discussion following Theorem 3.7, we have not been able to show whether \(\mathbb{V}_{i} (\cdot ; \mathbb{R}_{-i})\) is concave; therefore, the first-order conditions do not immediately imply optimality.) Fixing \(\mathbb{R}\in \mathcal{P}\) and assuming the stated conditions, we further show that \(\mathbb{V}_{i} (\mathbb{R}; \mathbb{R}_{-i}) \leq \mathbb{V}_{i} (\mathbb{R}^{\mathrm{r}}_{i}; \mathbb{R}_{-i})\).
Define \(X \mathrel{\mathop{:}}=\lambda_{i} \log (\mathrm{d}\mathbb{R}/ \mathrm{d}\mathbb{R}^{\mathrm{r}}_{i})\). Similarly to the arguments in Sect. A.2.1, the contract that agent \(i \in I\) would obtain by the response \(\mathbb{R}\in \mathcal{P}\) would be
where \(\mathbb{Q}^{X} \in \mathcal{P}\) is such that \(\log (\mathrm{d} \mathbb{Q}^{X} / \mathrm{d}\mathbb{Q}_{i}^{\mathrm{r}}) \sim X\). It follows that
Remark A.1
If \(\mathbb{E}_{\mathbb{Q}_{i}^{\mathrm{r}}}[\exp ( X^{+} ) X^{+} ] = \infty \) was true (equivalently, since \(\exp ( X ) X \) is bounded below if \(\mathbb{E}_{\mathbb{Q}_{i}^{\mathrm{r}}}[\exp ( X ) X ] = \infty \) was true), we would necessarily have that \(\mathbb{E}_{ \mathbb{Q}_{i}^{\mathrm{r}}}[ \exp ( X ) C^{\mathrm{r}}_{i} ] = - \infty \), which is clearly impossible in view of \(C^{\mathrm{r}}_{i} > - \delta_{-i}\) and \(\mathbb{E}_{\mathbb{Q}_{i}^{\mathrm{r}}}[\exp ( X )] < \infty \). It follows that \(\mathbb{E}_{\mathbb{Q}_{i}^{ \mathrm{r}}}[\exp ( X^{+} ) X^{+} ] < \infty \).
Since \(C^{\mathrm{r}}_{i} > - \delta_{-i}\), the \((0, \infty )\)-valued random variable \(D^{\mathrm{r}}_{i} \mathrel{\mathop{:}}=1 + C^{ \mathrm{r}}_{i} / \delta_{-i}\) is well defined. From (3.5), it follows that \(- C^{\mathrm{r}} _{i} / \delta_{i} \sim \log (\mathrm{d}\mathbb{Q}_{i}^{\mathrm{r}}/ \mathrm{d}\mathbb{P}_{i}) + \log D^{\mathrm{r}}_{i}\); since \(\mathbb{E}_{\mathbb{Q}_{i}^{\mathrm{r}}}[D^{\mathrm{r}}_{i}] = 1\), we have that \(\exp (- C^{\mathrm{r}}_{i} / \delta_{i}) = \mathbb{E}_{ \mathbb{P}_{i}}[\exp (- C^{\mathrm{r}}_{i} / \delta_{i})](\mathrm{d} \mathbb{Q}_{i}^{\mathrm{r}}/ \mathrm{d}\mathbb{P}_{i})D^{\mathrm{r}} _{i}\). Therefore, we obtain
Combining the previous, including (A.5) and Remark A.1, it suffices to show that
whenever \(X \in \mathbb{L}^{0}\) satisfies \(\mathbb{E}_{\mathbb{Q}_{i} ^{\mathrm{r}}}[\exp ( X^{+} ) X^{+} ] < \infty \). Since \(D^{ \mathrm{r}}_{i} > 0\) and \(\mathbb{E}_{\mathbb{Q}_{i}^{ \mathrm{r}}}[ D^{\mathrm{r}}_{i} ] = 1\), applying Jensen’s inequality under the probability having density \(D^{\mathrm{r}}_{i}\) with respect to \(\mathbb{Q}_{i}^{\mathrm{r}}\) gives \(- \delta_{i} \log \mathbb{E} _{\mathbb{Q}_{i}^{\mathrm{r}}}[ D^{\mathrm{r}}_{i} \exp (- \delta_{-i} X / \delta_{i} ) ] \leq \delta_{-i} \mathbb{E}_{\mathbb{Q}_{i}^{ \mathrm{r}}}[D^{\mathrm{r}}_{i} X]\). (In particular, we obtain \(\mathbb{E}_{\mathbb{Q}_{i}^{\mathrm{r}}}[ D^{\mathrm{r}}_{i} X^{-} ] < \infty \).) On the other hand, defining \(\chi \mathrel{\mathop{:}}= \log \mathbb{E}_{\mathbb{Q}_{i}^{\mathrm{r}}}[\exp ( X )] \in \mathbf{R}\) gives
where the last equality uses \(\mathbb{E}_{\mathbb{Q}_{i}^{\mathrm{r}}}[ \exp ( X - \chi ) ] = 1 = \mathbb{E}_{\mathbb{Q}_{i}^{\mathrm{r}}}[ D ^{\mathrm{r}}_{i} ]\) and \(C^{\mathrm{r}}_{i} = \delta_{-i} (D^{ \mathrm{r}}_{i} - 1)\). Using the inequality \(\exp (x) \geq 1 + x\) for \(x \in \mathbf{R}\), we obtain
(In particular, \(\mathbb{E}_{\mathbb{Q}_{i}^{\mathrm{r}}}[ D^{ \mathrm{r}}_{i} X^{+} ] < \infty \), which implies \(\mathbb{E}_{ \mathbb{Q}}[ D^{\mathrm{r}}_{i} X ] \in \mathbf{R}\).) Putting everything together, it follows that it suffices to show for \(X \in \mathbb{L} ^{0}\) with \(\mathbb{E}_{\mathbb{Q}_{i}^{\mathrm{r}}}[\exp ( X ^{+} ) X^{+} ] < \infty \) that \(\log \mathbb{E}_{\mathbb{Q}_{i}^{ \mathrm{r}}}[\exp ( X )] \leq \mathbb{E}_{\mathbb{Q}_{i}^{\mathrm{r}}}[ \exp (X ) X ] / \mathbb{E}_{\mathbb{Q}_{i}^{\mathrm{r}}}[\exp (X ) ]\). This follows from Jensen’s inequality applied to the convex function \((0, \infty ) \ni z \mapsto \phi (z) = z \log z\); then \(\phi ( \mathbb{E}_{\mathbb{Q}_{i}^{\mathrm{r}}}[\exp (X)]) \leq \mathbb{E} _{\mathbb{Q}_{i}^{\mathrm{r}}}[\phi (\exp (X))]\), which is exactly what was required. □
1.3 A.3 Proof of Theorem 3.7
Define \(R_{-i} \mathrel{\mathop{:}}=(1 / \lambda_{-i}) \sum_{j \in I \setminus \left\{ i\right\} } \lambda_{j} \log ( \mathrm{d}\mathbb{R}_{j} / \mathrm{d}\mathbb{P}_{i})\) and note that Hölder’s inequality gives \(\exp (R_{-i}) \in \mathbb{L}^{1}( \mathbb{P}_{i})\). For \(z_{i} \in \mathbf{R}\), implicitly define \(C_{i} (z_{i}) \in \mathbb{L}^{0}\) as the \((- \delta_{-i}, \infty )\)-valued random variable satisfying the equation
Note that the existence and uniqueness of the solution \(C_{i}(z_{i})\) for each \(z_{i} \in \mathbf{R}\) follows from the fact that the function \((- 1, \infty ) \ni y \mapsto (\delta / \delta_{i} ) y + \log (1 + y)\) is strictly increasing from \(- \infty \) to \(\infty \). For \(z_{i} \in \mathbf{R}\), define also the \((0, \infty )\)-valued random variable \(D_{i} (z_{i}) \mathrel{\mathop{:}}=1 + C_{i} (z_{i}) / \delta_{-i}\) and note that it is the unique solution to the equation
Observe that \(D_{i}\) (and hence \(C_{i}\)) is increasing as a function of \(z_{i}\). It is also straightforward to check that \(\mathbb{L}^{0} \mbox{-} \lim_{z_{i} \to - \infty } D_{i} (z_{i}) = 0\) and \(\mathbb{L}^{0} \mbox{-} \lim_{z_{i} \to \infty } D_{i} (z_{i}) = \infty \).
Lemma A.2
For all \(z_{i} \in \mathbf{R}\), we have
In particular, both \(D_{i} (z_{i})^{-\lambda_{i}} \exp (\lambda_{-i} R _{-i})\) and \(D_{i} (z_{i})^{\lambda_{-i}} \exp (\lambda_{-i} R_{-i})\) are in \(\mathbb{L}^{1}(\mathbb{P}_{i})\).
Proof
Fix \(z_{i} \in \mathbf{R}\). By (A.6), \(\log D_{i} (z_{i}) \geq z_{i} - R_{-i}\) on \(\left\{ D_{i} (z_{i}) < 1\right\} \), whereas \(\log D_{i} (z_{i}) \leq z_{i} - R_{-i}\) on \(\left\{ D_{i} (z_{i}) \geq 1\right\} \). These observations verify inequalities (A.7). Since \(D_{i}(z_{i})^{-1} \leq 1 \vee \exp (- z_{i} + R_{-i})\) and \(\exp (R_{-i}) \in \mathbb{L}^{1}(\mathbb{P}_{i})\), \(D_{i}(z_{i})^{-1} \in \mathbb{L} ^{1}(\mathbb{P}_{i})\) follows; then, in view of Hölder’s inequality, we obtain that \(D_{i} (z_{i})^{-\lambda_{i}} \exp (\lambda_{-i} R_{-i}) \in \mathbb{L}^{1}(\mathbb{P}_{i})\). Furthermore, we have the estimate
which implies that \(D_{i} (z_{i})^{\lambda_{-i}} \exp (\lambda_{-i} R _{-i}) \in \mathbb{L}^{1}(\mathbb{P}_{i})\) since \(\exp (R_{-i}) \in \mathbb{L}^{1}(\mathbb{P}_{i})\). □
In view of Lemma A.2, for each \(z_{i} \in \mathbf{R}\), we may define \(\mathbb{Q}_{i} (z_{i}) \in \mathcal{P}\) via
in other words,
Furthermore, for every \(z_{i} \in \mathbf{R}\), Lemma A.2 and in particular the fact that we have \(D_{i} (z_{i})^{\lambda_{-i}} \exp (\lambda_{-i} R_{-i})\in \mathbb{L}^{1}(\mathbb{P}_{i})\) imply \(D_{i}(z_{i}) (\mathrm{d} \mathbb{Q}_{i}(z_{i}) / \mathrm{d}\mathbb{P}_{i}) \in \mathbb{L}^{1}( \mathbb{P}_{i})\), which in turn implies that \(D_{i}(z_{i}) \in \mathbb{L}^{1}(\mathbb{Q}_{i}(z_{i}))\).
As mentioned in the discussion following Proposition 3.2, to establish Theorem 3.7, we need to show that there exists a unique \(\zeta_{i} \in \mathbf{R}\) with \(\mathbb{E}_{\mathbb{Q} _{i} (\zeta_{i})} [ D_{i} (\zeta_{i}) ] = 1\). Define \(f_{i} : \mathbf{R}\to (0, \infty ]\) via \(f_{i} (z_{i}) = \mathbb{E} _{\mathbb{Q}_{i} (z_{i})} [ D_{i} (z_{i}) ]\). Since \(D_{i}(z_{i}) \in \mathbb{L}^{1}(\mathbb{Q}_{i} (z_{i}))\) for all \(z_{i} \in \mathbf{R}\), it follows that \(f_{i}(z_{i}) < \infty \) for all \(z_{i} \in \mathbf{R}\). It is straightforward to check that \(f_{i}\) is continuous by the dominated convergence theorem and Lemma A.2.
Let \(\overline{\mathbb{P}}_{i}\) be the probability measure in \(\mathcal{P}\) such that \(\log (\mathrm{d}\overline{\mathbb{P}}_{i} / \mathrm{d}\mathbb{P}_{i}) \sim R_{-i}\). Then, thanks to the equivalence relation \(\log ( \mathrm{d}\mathbb{Q}_{i}(z_{i}) / \mathrm{d} \mathbb{P}_{i}) \sim D_{i}(z_{i}) + R_{-i}\), we have that
for all \(z_{i} \in \mathbf{R}\). In fact, since the covariance of \(\exp (D_{i}(z_{i}))\) and \(D_{i}(z_{i})\) is nonnegative under any probability, we have \(f_{i}(z_{i})\geq \mathbb{E}_{\overline{ \mathbb{P}}_{i}} [ D_{i} (z_{i})]\) for all \(z_{i} \in \mathbf{R}\). Using monotone convergence and (A.8), \(\lim_{z_{i} \to \infty } f _{i}(z_{i}) = \infty \) follows from \(\lim_{z_{i} \to \infty } D_{i}(z _{i}) = \infty \). Furthermore, \(\lim_{z_{i} \to - \infty } D_{i} (z _{i}) = 0\) and monotone convergence imply that we have \(\lim_{z_{i} \to - \infty } \mathbb{E}_{\overline{\mathbb{P}}_{i}} [ \exp (D_{i}(z_{i}))] = 1\) and \(\lim_{z_{i} \to - \infty } \mathbb{E}_{\overline{\mathbb{P}}_{i}} [\exp (D_{i}(z_{i})) D_{i}(z _{i})] = 0\), from which we obtain \(\lim_{z_{i} \to - \infty } f_{i} (z _{i}) = 0\). It follows that there exists at least one \(\zeta_{i} \in \mathbf{R}\) with \(f_{i} (\zeta_{i}) = 1\). We claim that \(f_{i}\) is strictly increasing, which implies that \(\zeta_{i}\) is indeed unique. In preparation, note that differentiating (A.6) with respect to \(z_{i}\) and rearranging give \(D_{i}' (z_{i}) = q_{i} (D_{i} (z_{i}))\), where \((0, \infty ) \ni y \mapsto q_{i}(y) \mathrel{\mathop{:}}=\lambda_{i} y / (\lambda_{i} + y)\). In particular, since \(q_{i}\) is an increasing function, the covariance between \(D_{i}'(z_{i})\) and \(D_{i}(z_{i})\) is nonnegative for all \(z_{i} \in \mathbf{R}\) under any probability. Straightforward computations using the definition of \(\mathbb{Q}_{i} (z _{i})\) give that the derivative of \(f_{i}\) satisfies
for \(z_{i} \in \mathbf{R}\). Rearranging, \(f_{i}' (z_{i}) = \mathbb{E} _{\mathbb{Q}_{i} (z_{i})} [D_{i}'(z_{i}) ] + \mathrm{Cov}_{\mathbb{Q} _{i} (z_{i})} ( D_{i}(z_{i}), D_{i}'(z_{i}) )\) for \(z_{i} \in \mathbf{R}\). Since \(D_{i}'(z_{i}) > 0\) and \(\mathrm{Cov}_{\mathbb{Q} _{i} (z_{i})} ( D_{i}(z_{i}), D_{i}'(z_{i}) ) \geq 0\) for all \(z_{i} \in \mathbf{R}\), Theorem 3.7 has been proved. □
1.4 A.4 Proof of Theorem 4.2
Suppose that \((\mathbb{Q}^{\diamond }, (C^{\diamond }_{i})_{i \in I})\) is a Nash equilibrium and let \((\mathbb{R}^{\diamond }_{i})_{i \in I} \in \mathcal{P}^{I}\) be the associated revealed subjective beliefs. We first prove relationship (4.3). In view of Proposition 3.2, since \(C^{\diamond }_{i} / \delta _{i} \sim \log (\mathrm{d}\mathbb{R}^{\diamond }_{i} / \mathrm{d} \mathbb{Q}^{\diamond })\) and
(3.2) gives
that is, \(\log ( \mathrm{d}\mathbb{R}^{\diamond }_{i} / \mathrm{d} \mathbb{P}_{i}) \sim - \log (1 + C^{\diamond }_{i} / \delta_{-i} )\) for all \(i \in I\), which is (4.5). Since \(\log ( \mathrm{d}\mathbb{P}_{i} / \mathrm{d}\mathbb{Q}^{\ast }) \sim C^{\ast }_{i} / \delta_{i}\) for all \(i \in I\) in view of Eq. (2.4), it follows that
for all \(i \in I\). In turn, since \(\sum_{j \in I} C^{\ast }_{j} = 0\), the latter gives
which in view of (4.5) is exactly (4.3).
To prove (4.2), we add \(\lambda_{i} \log (1 + C^{\diamond }_{i} / \delta_{-i} ) \sim - \lambda_{i} \log ( \mathrm{d}\mathbb{R} ^{\diamond }_{i} / \mathrm{d}\mathbb{P}_{i})\) to (3.2) and obtain
Combined with (4.3), this gives (4.2) for an appropriate tuple \(z^{\diamond }:= (z^{\diamond }_{i})_{i \in I} \in \mathbf{R}^{I}\). The market clearing conditions \(\sum_{i \in I} C^{\diamond }_{i} = 0 = \sum_{i \in I} C^{\ast }_{i}\) show that \(\sum_{i \in I} z^{\diamond }_{i} = 0\), that is, \(z^{\diamond }\in \Delta^{I}\). Finally, the fact that \(\mathbb{E}_{\mathbb{Q}^{ \diamond }}[C^{\diamond }_{i}] = 0\) for all \(i \in I\) results directly from \((C^{\diamond }_{i})_{i \in I} \in \mathcal{C}_{\mathbb{Q}^{ \diamond }}\).
For the proof of the converse implication, assume that conditions (N1)–(N3) hold for \((\mathbb{Q}^{\diamond }, (C^{\diamond }_{i})_{i \in I})\) and fix \(i \in I\). Define the associated revealed beliefs \((\mathbb{R}^{\diamond }_{i})_{i \in I} \in \mathcal{P}^{I}\) via \(\log ( \mathrm{d}\mathbb{R}^{\diamond }_{i} / \mathrm{d}\mathbb{Q} ^{\diamond }) \sim C^{\diamond }_{i} / \delta_{i}\). Since \(C^{\ast } _{i} / \delta_{i} \sim \log ( \mathrm{d}\mathbb{P}_{i} / \mathrm{d} \mathbb{Q}^{\ast })\), a combination of (4.2) and (4.3) gives that \(\log (1 + C^{\diamond }_{i} / \delta _{-i} ) \sim - \log ( \mathrm{d}\mathbb{R}^{\diamond }_{i} / \mathrm{d}\mathbb{P}_{i})\). Using again (4.2) and (4.3), we have
It follows that the sufficient conditions for optimality of Proposition 3.2 are satisfied for each \(i \in I\). To show that \((\mathbb{Q}^{\diamond }, (C^{\diamond }_{i})_{i \in I})\) is a Nash equilibrium, it is left to verify that \((C^{\diamond }_{i})_{i \in I}\in \mathcal{C}_{\mathbb{Q}^{\diamond }}\). Indeed, summing (4.2) with respect to \(i\) implies that \(\sum_{i \in I}C ^{\diamond }_{i}=0\) since \(z^{\diamond }\) is assumed to belong in \(\Delta^{I}\). This fact, together with the requirement \(C^{\diamond } _{i}>-\delta_{-i}\), implies the uniform boundedness of \(C^{\diamond } _{i}\); in particular, \(\exp (C^{\diamond }_{i}/\delta_{i})\in \mathbb{L}^{1}(\mathbb{Q}^{\diamond })\) for all \(i \in I\). Taking also (N3) into account, we conclude that \((C^{\diamond }_{i})_{i \in I} \in \mathcal{C}_{\mathbb{Q}^{\diamond }}\), which completes the proof. □
1.5 A.5 Proof of Proposition 4.5
Fix \(z \in \Delta^{I}\). Suppose for the moment that a solution to (4.17) exists, and set
Then, with \(\eta_{i} : (0, \infty ) \to \mathbf{R}\) defined via \(\eta_{i} (x) = \delta_{-i} (x - 1) + \delta_{i} \log x\), (4.17) implies that \(\eta_{i} (1 + C_{i}(z)/ \delta_{-i}) = z_{i} + C^{\ast }_{i} + \delta_{i} L(z)\) for all \(i \in I\). With \(\theta_{i} : \mathbf{R}\to (0, \infty )\) denoting the inverse of \(\eta_{i}\) for all \(i \in I\), it follows that
Plugging back into the definition of \(L(z)\) in (A.9), we obtain that
should be satisfied.
We now proceed backwards by showing that (A.11) has a unique solution. In what follows, fix \(z \in \Delta^{I}\) and define the function \(w : \Omega \times \mathbf{R}\to \mathbf{R}\) via the recipe \(w(y) = y - \sum_{i \in I} \lambda_{i} \log \theta_{i} (z_{i} + C^{ \ast }_{i} + \delta_{i} y)\) for \(y \in \mathbf{R}\), where the dependence of \(w\) on \(\omega \in \Omega \) is suppressed. The derivative of \(w\) with respect to the spatial coordinate is
Since \(\theta_{i} (y)\) behaves sublinearly as \(y \to \infty \), \(\lim_{y \uparrow \infty } w(y) = \infty \) follows in a straightforward way. Furthermore, by the definition of \(\theta_{i}\), for all \(x \in (- \infty , 0)\) and \(i \in I\), we have \(x < \delta_{i} \log \theta_{i}(x)\). This implies \(w (y) < y - \sum_{i \in I} (1/ \delta )( z_{i} + C^{\ast }_{i} + \delta_{i} y) = 0\) on the event \(\{y < - \bigvee_{j \in I} ((z_{j} + C^{\ast }_{j}) / \delta_{j})\}\), showing at the same time that the equation \(w (L(z)) = 0\) has a unique solution and
Given the existence of a unique \(L (z)\) solving (A.11), \(C_{i} (z)\) is specified for all \(i \in I\) via (A.10).
Since \(\exp ( C^{\ast }_{i} / \delta_{i}) \in \mathbb{L}^{1}( \mathbb{Q}^{\ast })\) for all \(i\), it is clear that \(\exp ( \bigvee_{i \in I} C^{\ast }_{i} / \delta_{i}) \in \mathbb{L}^{1}( \mathbb{Q}^{\ast })\). Thus combining (A.12) and the equality \(\prod_{j \in I} (1 + C_{j}(z) / \delta_{-j} )^{- \lambda_{j}} = \exp (- L(z))\) implies the validity of (4.18), which concludes the proof. □
1.6 A.6 Proof of Theorem 4.7
We first establish the general existence result and then tackle uniqueness in the two-agent case.
1.6.1 A.6.1 Proof of existence of a Nash equilibrium
We use the notation from Proposition 4.5 and the discussion following it. For all \(z \in \Delta^{I}\) and \(i \in I\), define \(u_{i}(z) \mathrel{\mathop{:}}=\mathbb{U}_{i} (C _{i}(z))\). Furthermore, for each \(z \in \Delta^{I}\), define \(u(z) \mathrel{\mathop{:}}=\sum_{i \in I}u_{(}z)\) and
Note that \(\sum_{i \in I}\phi_{i} (z) = 0\) for all \(z \in \Delta^{I}\), so that \(\phi := (\phi_{i})_{i \in I}\) is \(\Delta^{I}\)-valued. The obvious continuity of \(\Delta^{I}\ni z \mapsto L(z)\) from (A.11) and the domination relation given by (A.12) allow the application of the dominated convergence theorem to establish that \(\phi : \Delta^{I}\to \Delta^{I}\) is a continuous function.
Lemma A.3
\(z^{\diamond }\in \Delta^{I}\) corresponds to a Nash equilibrium if and only if it is a fixed point of \(\phi \).
Proof
In view of the discussion in Sect. 4.3.4, if \(z^{\diamond }\in \Delta^{I}\) corresponds to a Nash equilibrium, then \(z^{\diamond }\) is a fixed point of \(\phi \). Conversely, we show that any fixed point of \(\phi \) corresponds to a Nash equilibrium. With \(L(z)\) as in (A.9) and recalling (4.17), start by observing that
From the last equality, it follows that
Adding up the previous equality over all agents, we obtain
Since \(\log (\mathrm{d}\mathbb{Q}(z) / \mathrm{d}\mathbb{Q}^{\ast }) = - L(z) + \lambda (z)\) for appropriate \(\lambda (z) \in \mathbf{R}\) and the equality \(\phi_{i}(z) - z_{i} = u_{i}(z) - z_{i} - u^{\ast }_{i} - \lambda_{i} (u(z) - u^{\ast })\) holds for all \(i \in I\) and \(z \in \Delta^{I}\), it follows that for all \(i \in I\) and \(z \in \Delta^{I}\),
where we note that the quantity \(\lambda (z)\) cancels in this equation. Now suppose that \(z^{\diamond }\in \Delta^{I}\) is a fixed point of \(\phi \). From the last equality, it follows that the quantities \(\mathbb{E}_{\mathbb{Q}(z^{\diamond })} [1 + C_{i}(z^{\diamond }) / \delta_{-i}]\) have the same value, which we call \(x(z^{\diamond })\), for all \(i \in I\). In other words, \(\mathbb{E}_{\mathbb{Q}(z^{\diamond })} [C_{i}(z^{\diamond })] = \delta_{-i} (x(z^{\diamond }) - 1)\) for all \(i \in I\). Since \(\sum_{i \in I}C_{i}(z^{\diamond }) = 0\), we obtain that \(x(z^{\diamond }) = 1\), which implies that \(\mathbb{E}_{ \mathbb{Q}(z^{\diamond })} [C_{i}(z^{\diamond })] = 0\) for all \(i \in I\), in turn implying that \(z^{\diamond }\) corresponds to a Nash equilibrium. □
In view of Lemma A.3, the existence of a Nash equilibrium follows if we can show that \(\phi \) has at least one fixed point. For any \(z \in \Delta^{I}\) and \(i \in I\), the strong bound \(C_{i}(z) > - \delta_{-i}\) implies \(u_{i}(z) \geq - \delta_{-i}\). Furthermore, \(u(z) \leq u^{\ast }\) for all \(z \in \Delta^{I}\) by aggregate optimality of an Arrow–Debreu equilibrium. Therefore, it follows that
Define the set \(K \mathrel{\mathop{:}}=\{z \in \Delta^{I}\, | \,z_{i} \geq - \delta_{-i} - u^{\ast }_{i}, \ \forall i \in I\}\) and note that \(K\) is a compact and convex subset of \(\Delta^{I}\). Since \(\phi \) is continuous and maps \(K\) to \(K\), Brouwer’s fixed point theorem implies that \(\phi \) has at least one fixed point on \(K\), which establishes the claim. (In fact, according to the discussion in Sect. 4.3.4, any fixed point must actually lie in the smaller set \(\{z \in \Delta^{I}\, | \,z_{i} \geq - u^{ \ast }_{i}, \ \forall i \in I\}\).) □
1.6.2 A.6.2 Proof of uniqueness in the two-agent case
Note that \((z_{0}, z_{1}) \in \Delta^{I}\) if and only if \(z_{0} = - z _{1}\). In the course of the proof, we identify \(\mathbf{R}\) and \(\Delta^{I}\) via \(\mathbf{R}\ni z \leftrightarrow (z, - z) \in \Delta ^{I}\), that is, by considering only the “zero” coordinate. Correspondingly, for \(z \in \mathbf{R}\), we write \(C_{i}(z)\) instead of \(C_{i} ((z, -z))\) for \(i \in \left\{ 0,1\right\} \); similarly, for \(z \in \mathbf{R}\), we write \(L(z)\) instead of \(L(z, -z)\) in (A.9).
In view of Proposition 4.6 and the equality \(C_{1}(z) = - C_{0}(z)\) for all \(z \in \mathbf{R}\), we need to prove the existence of a unique \(z^{\diamond }\in \mathbf{R}\) such that \(\mathbb{E}_{\mathbb{Q}(z^{\diamond })} [C_{0}(z^{\diamond })] = 0\); since the existence was already established, we only focus on the uniqueness here. Define the continuous function \(\mathbf{R}\ni z \mapsto f_{0} (z) = \mathbb{E}_{\mathbb{Q}(z)}[C_{0}(z)]\); then, it suffices to show that \(f_{0}\) is strictly increasing.
Recall that \(C_{1} (z) = - C_{0}(z)\) for all \(z \in \mathbf{R}\) and rewrite (4.17) as
Differentiating with respect to \(z \in \mathbf{R}\), we obtain after some algebra that
Since \(-\delta_{1} < C_{0}(z)<\delta_{0}\), \(C_{0}' (z)\) is clearly a \((0, \infty )\)-valued random variable for all \(z \in \mathbf{R}\). Furthermore, since \(L(z) = \lambda_{0} \log (1 + C_{0} (z) / \delta _{1}) + \lambda_{1} \log (1 - C_{0} (z) / \delta_{0})\) for \(z \in \mathbf{R}\), differentiation and simple algebra give
In other words, upon defining \(q(x) = (x + \delta_{1} - \delta_{0}) / (\delta_{0} \delta_{1} + (\delta_{1} + x) (\delta_{0} - x))\) for \(x \in (-\delta_{1}, \delta_{0})\), \(L'(z) = - q(C_{0}(z))\) for all \(z \in \mathbf{R}\). Since
for all \(x \in (-\delta_{1}, \delta_{0})\), the covariance between \(C_{0}(z)\) and \(- L'(z)\) is nonnegative under any probability for all \(z \in \mathbf{R}\). Continuing, if we take into account that
for all \(i \in I\), it is straightforward to compute that for all \(z \in \mathbf{R}\), we have
Since \(C_{0}' (z)\) is a \((0, \infty )\)-valued random variable and \(\mathrm{Cov}_{\mathbb{Q}(z)} (C_{0} (z), L'(z) ) \leq 0\) for all \(z \in \mathbf{R}\), the claim is proved. □
1.7 A.7 Proof of Proposition 5.2
For the remainder of the Appendix , we define \(\delta^{m} \mathrel{\mathop{:}}=\delta^{m}_{0} + \delta_{1}\), \(\lambda^{m}_{0} \mathrel{\mathop{:}}=\delta^{m}_{0} / \delta^{m}\) and \(\lambda_{1}^{m} \mathrel{\mathop{:}}=\delta_{1} / \delta^{m} = 1 - \lambda_{0}^{m}\) for all \(m \in \mathbf{N}\). In view of Theorem 2.2 and the fact that we have \(\mathbb{L}^{0} \mbox{-} \lim_{m \to \infty }(\mathrm{d}\mathbb{Q}^{m, \ast }/ \mathrm{d} \mathbb{P}_{0}) = 1\), we need to focus on the limit of the sequence \((\mathcal{H}(\mathbb{Q}^{m, \ast }\, | \,\mathbb{P}_{1}))_{m \in \mathbf{N}}\). For each \(m \in \mathbf{N}\), similarly to (5.1), we have
Therefore, with \(Z \mathrel{\mathop{:}}=\mathrm{d}\mathbb{P}_{0} / \mathrm{d}\mathbb{P}_{1}\) and \(\phi (x) = x \log x\), we have
Under Assumption 5.1, the fact that \(\lim_{m \to \infty }\lambda_{0}^{m} = 1\) and the dominated convergence theorem give that \(\lim_{m \to \infty }\mathcal{H}(\mathbb{Q}^{m, \ast }\, | \, \mathbb{P}_{1}) = \mathbb{E}_{\mathbb{P}_{1}} [\phi (Z) ] = \mathcal{H}(\mathbb{P}_{0} \, | \,\mathbb{P}_{1})\). Since
the limiting relationship \(C^{\infty , \ast }_{0} = \delta_{1} \log ( \mathrm{d}\mathbb{P}_{0} / \mathrm{d}\mathbb{P}_{1}) - \delta_{1} \mathcal{H}(\mathbb{P}_{0} \, | \,\mathbb{P}_{1})\) readily follows.
Continuing, for \(m \in \mathbf{N}\), note that \(u^{m, \ast }_{0} = \mathbb{U}_{0} (C^{m, \ast }_{0}) \leq \mathbb{E}_{\mathbb{P}_{0}} [C ^{m, \ast }_{0}]\). Note that there exists \(c > 0\) such that \(\sup_{m \in \mathbf{N}} |C^{m, \ast }_{0}| \leq c (1 + \left\vert \log ( \mathrm{d}\mathbb{P}_{0} / \mathrm{d}\mathbb{P}_{1})\right\vert )\). Under Assumption 5.1, we have \(\log (\mathrm{d}\mathbb{P} _{0} / \mathrm{d}\mathbb{P}_{1}) \in \mathbb{L}^{1} (\mathbb{P}_{0})\), which means that the dominated convergence theorem can be applied and gives \(\limsup_{m \to \infty } u^{m, \ast }_{0} \leq \mathbb{E}_{ \mathbb{P}_{0}} [C^{\infty , \ast }_{0}] = 0\). Since \(0 \leq u^{m, \ast }_{0}\) for all \(m \in \mathbf{N}\), \(\lim_{m \to \infty } u^{m, \ast }_{0} = 0\) follows.
Moving on to agent 1, the fact that \(u^{m, \ast }_{1} = \delta_{1} \mathcal{H}(\mathbb{Q}^{m, \ast }\, | \,\mathbb{P}_{1})\) for all \(m \in \mathbf{N}\) and the previous discussion give \(\lim_{m \to \infty } u^{m, \ast }_{1} = \delta_{1} \mathcal{H}(\mathbb{P}_{0} \, | \,\mathbb{P}_{1})\). The proof is complete. □
1.8 A.8 Proof of Lemma 5.3
Since \((-1, \infty ) \ni x \mapsto x + \log (1 + x)\) is strictly increasing and continuous and maps \((-1, \infty )\) to \((- \infty , \infty )\), it follows that \(\mathbb{L}^{0} \mbox{-} \lim_{z \to - \infty } C^{\infty }_{0}(z) = - \delta_{1}\) and \(\mathbb{L} ^{0} \mbox{-} \lim_{z \to \infty } C^{\infty }_{0}(z) = \infty \). Let \(D^{\infty }_{0}(z) \mathrel{\mathop{:}}=1 + C^{\infty }_{0}(z) / \delta_{1}\) for all \(z \in \mathbf{R}\). On \(\{C^{\infty }_{0}(z) > 0 \}\), we have \(1/D^{\infty }_{0}(z) \leq 1\). On \(\{C^{\infty }_{0} (z) \leq 0\}\), we have
which implies that
Since \(1/D^{\infty }_{0}(z) \leq 1 \vee \exp ( \mathcal{H}(\mathbb{P} _{0} \, | \,\mathbb{P}_{1}) - z / \delta_{1}) (\mathrm{d}\mathbb{P} _{1} / \mathrm{d}\mathbb{P}_{0})\) everywhere, Assumption 5.1 implies that the function
is \((0, \infty )\)-valued, continuous, strictly decreasing and, in view of the limiting behaviour of \(\mathbf{R}\ni z \mapsto C^{\infty }_{0}(z)\) and the monotone convergence theorem, maps \(\mathbf{R}\) to \((0, \infty )\). Therefore, the result follows. □
1.9 A.9 Proof of Theorem 5.4
To ease the reading, throughout the proof, for all \(m \in \mathbf{N}\), define the \((0, \!1 / \lambda^{m}_{1})\)-valued random variable \(D^{m, \diamond }_{0} \mathrel{\mathop{:}}=1 + C^{m, \diamond }_{0} / \delta_{1}\) and the \((0, \infty )\)-valued random variable \(D_{0}^{m,\mathrm{r}}\mathrel{\mathop{:}}=1 + C_{0}^{m, \mathrm{r}}/ \delta_{1}\). We use the obvious notation \(\mathbb{Q}^{m, \diamond }\in \mathcal{P}\) for \(m \in \mathbf{N}\). As in (3.5), let \(\mathbb{Q}_{0}^{m,\mathrm{r}} \in \mathcal{P}\) be defined via
and recall that \(\mathbb{E}_{\mathbb{Q}_{0}^{m,\mathrm{r}}} [C_{0} ^{m,\mathrm{r}}] = 0\) for all \(m \in \mathbf{N}\), as follows from Proposition 3.2.
For each \(m \in \mathbf{N}\), define \(w^{m} : (0, \infty ) \to \mathbf{R}\) and \(\phi^{m} : (0, 1 / \lambda^{m}_{1}) \to \mathbf{R}\) by
By the equivalence \(C^{m, \ast }_{0}\sim \delta^{m}_{0}\log ( \mathrm{d}\mathbb{P}_{0}/\mathrm{d}\mathbb{Q}^{m, \ast })\sim \delta ^{m}_{0}\lambda^{m}_{1}\log (\mathrm{d}\mathbb{P}_{0}/\mathrm{d} \mathbb{P}_{1})\), (3.2) and (4.4), note that
for an appropriate sequence \((z_{0}^{m,\mathrm{r}})_{m \in \mathbf{N}}\) from Theorem 3.7 and the sequence \((z^{m, \diamond }_{0})_{m \in \mathbf{N}}\) from Theorem 4.2. The next two lemmas show in particular that \((z^{m, \diamond }_{0})_{m \in \mathbf{N}}\) and \((z_{0}^{m,\mathrm{r}})_{m \in \mathbf{N}}\) are bounded.
Lemma A.4
The sequence \((z^{m, \diamond }_{0})_{m \in \mathbf{N}}\) is bounded, and there exists \(a \in \mathbf{R}\) such that
Proof
Note that \(\mathbb{E}_{\mathbb{Q}^{m, \diamond }} [C^{m, \diamond } _{0}] = 0\) is equivalent to \(\mathbb{E}_{\mathbb{Q}^{m, \diamond }} [ D^{m, \diamond }_{0} ] = 1\) for all \(m \in \mathbf{N}\).
Applying (4.2) for \(i=1\) and using the fact that \(C^{m, \ast }_{1}/ \delta_{1} \sim \log (\mathrm{d}\mathbb{P}_{1} / \mathrm{d}\mathbb{Q}^{m, \ast })\) and (4.3), it follows that
Coupling the last equivalence with \(C^{m, \diamond }_{1} / \delta_{1} = - C^{m, \diamond }_{0} / \delta_{1} = 1 - D^{m, \diamond }_{0}\), after some algebra, we obtain \(\log ( \mathrm{d}\mathbb{Q}^{m, \diamond }/ \mathrm{d}\mathbb{P}_{1}) \sim D^{m, \diamond }_{0} - \log (1 - \lambda^{m}_{1} D^{m, \diamond }_{0} )\). Therefore, for all \(m \in \mathbf{N}\),
where the inequality \(\mathrm{Cov}_{\mathbb{P}_{1}} ( \exp (D^{m, \diamond }_{0})/ ( 1 - \lambda^{m}_{1} D^{m, \diamond }_{0} ) , D^{m, \diamond }_{0} ) \geq 0\), valid for all \(m \in \mathbf{N}\) in view of comonotonicity, was used. Since \(\mathbb{E}_{\mathbb{P}_{1}} [ D^{m, \diamond }_{0} ] \leq 1\) for all \(m \in \mathbf{N}\), \(( D^{m, \diamond }_{0})_{m \in \mathbf{N}}\) is \(\mathbb{L}^{0}\)-bounded.
Similarly, applying (4.2) (for \(i= 0\)), we obtain
or, equivalently, \(\log ( \mathrm{d}\mathbb{Q}^{m, \diamond }/ \mathrm{d}\mathbb{P}_{0}) \sim - \delta_{1} D^{m, \diamond }_{0} / \delta^{m}_{0} - \log D^{m, \diamond }_{0}\). For \(m \in \mathbf{N}\), it follows that
where the last inequality follows since \(\mathrm{Cov}_{\mathbb{P}_{0}} ( \exp (- \delta_{1} D^{m, \diamond }_{0} / \delta^{m}_{0} ) , 1/ D ^{m, \diamond }_{0} ) \geq 0\) for all \(m \in \mathbf{N}\). The fact that \(\mathbb{E}_{\mathbb{P}_{0}} [ 1 / D^{m, \diamond }_{0} ] \leq 1\) for all \(m \in \mathbf{N}\) implies that \((1 / D^{m, \diamond }_{0})_{m \in \mathbf{N}}\) is \(\mathbb{L}^{0}\)-bounded.
We then obtain that \((\log D^{m, \diamond }_{0})_{m \in \mathbf{N}}\) is bounded in \(\mathbb{L}^{0}\), from which it follows that the family \(\{\phi^{m} (D^{m, \diamond }_{0}) : m \in \mathbf{N}\}\) is bounded in \(\mathbb{L}^{0}\). As \((C^{m, \ast }_{0})_{m \in \mathbf{N}}\) converges in \(\mathbb{L}^{0}\), (A.16) implies that the family \(\{z^{m, \diamond }_{0} : m \in \mathbf{N}\}\) is bounded (in \(\mathbf{R}\)).
Continuing, since \(x \in (0,1)\) implies \(\phi^{m} (x) \leq \lambda _{0}^{m} \delta_{1} \log x\), it follows that
on the event \(\{D^{m, \diamond }_{0} \leq 1\}\). A combination of \(C^{m, \ast }_{0} = \delta_{0}^{m} \log (\mathrm{d}\mathbb{P}_{0} / \mathrm{d}\mathbb{Q}^{m, \ast }) + u^{m, \ast }_{0}\) and (5.1) gives
The second and third terms of the right-hand side of (A.18) converge (to \(- \mathcal{H}(\mathbb{P}_{0} \, | \,\mathbb{P}_{1})\) and zero, respectively), and the sequence \(( z^{m, \diamond }/ \lambda_{0}^{m})_{m \in \mathbf{N}}\) is bounded in \(\mathbf{R}\); therefore, the existence of \(a \in \mathbf{R}\) such that (A.17) holds readily follows. □
Lemma A.5
The sequence \((z_{0}^{m,\mathrm{r}})_{m \in \mathbf{N}}\) is bounded, and there exists \(c\in \mathbf{R}\) such that
Proof
Recall that \(\mathbb{E}_{\mathbb{Q}_{0}^{m,\mathrm{r}}} [ D_{0}^{m, \mathrm{r}}] = 1\) for all \(m \in \mathbf{N}\). In view of (3.2), we obtain
Further, \(\log ( \mathrm{d}\mathbb{Q}_{0}^{m,\mathrm{r}}/ \mathrm{d} \mathbb{P}_{0}) \sim - \lambda^{m}_{0} \log D_{0}^{m,\mathrm{r}}+ \lambda^{m}_{1} \log ( \mathrm{d}\mathbb{P}_{1} / \mathrm{d} \mathbb{P}_{0})\) due to (3.5). The last two facts give \(\log (\mathrm{d}\mathbb{Q}_{0}^{m,\mathrm{r}}/ \mathrm{d} \mathbb{P}_{1}) \sim D_{0}^{m,\mathrm{r}}\). Therefore, for \(m \in \mathbf{N}\),
where the last inequality follows from \(\mathrm{Cov}_{\mathbb{P}_{1}} ( \exp (D_{0}^{m,\mathrm{r}}), D_{0}^{m,\mathrm{r}}) \geq 0\) for all \(m \in \mathbf{N}\). It follows that \(\mathbb{E}_{\mathbb{P}_{1}} [ D _{0}^{m,\mathrm{r}}] \leq 1\) for all \(m \in \mathbf{N}\), which implies that \(( D_{0}^{m,\mathrm{r}})_{m \in \mathbf{N}}\) is \(\mathbb{L}^{0}\)-bounded. Hence, the family \(\{(w^{m} (D_{0}^{m,x}))^{+} : m \in \mathbf{N}\}\) is also bounded in \(\mathbb{L}^{0}\). Since \((C^{m, \ast }_{0})\) converges in \(\mathbb{L}^{0}\), (A.16) implies that \((z_{0}^{m,\mathrm{r}})_{m \in \mathbf{N}}\) is bounded from above (in \(\mathbf{R}\)).
By way of contradiction, suppose that \((z_{0}^{m,\mathrm{r}})_{m \in \mathbf{N}}\) is not bounded from below. Passing to a subsequence if necessary, we may assume that \((z_{0}^{m,\mathrm{r}})_{m \in \mathbf{N}}\) is a sequence of negative numbers with \(\lim_{m \to \infty }z_{0}^{m,\mathrm{r}}= -\infty \). Hence, again by (A.16), we get \(\lim_{m \to \infty }D_{0}^{m, \mathrm{r}}=0\). Since \(x + \log x \leq 1 / \lambda_{0}^{m} + (1 / \lambda_{0}^{m} \delta_{1}) w^{m}(x)\) for all \(x \geq 1\) and \(z_{0}^{m,\mathrm{r}}\leq 0\) for all \(m \in \mathbf{N}\), we get that for all \(m\), \(D_{0}^{m,\mathrm{r}}+ \log D_{0}^{m,\mathrm{r}} \leq 1 / \lambda_{0}^{m} + C^{m, \ast }_{0} / \lambda_{0}^{m} \delta _{1}\) on \(\{D_{0}^{m,\mathrm{r}}> 1\}\). Given (A.18), we conclude the existence of \(\kappa \in \mathbf{R}\) such that for all \(m \in \mathbf{N}\), \(D_{0}^{m, \mathrm{r}}+ \log D_{0}^{m,\mathrm{r}}\leq \kappa + \log (\mathrm{d} \mathbb{P}_{0} / \mathrm{d}\mathbb{P}_{1})\) on \(\{D_{0}^{m,\mathrm{r}}> 1\}\). It follows that we can use the dominated convergence theorem on the right-hand side of the equality \(\mathbb{E}_{\mathbb{Q}_{0}^{m, \mathrm{r}}} [ D_{0}^{m,\mathrm{r}}] = \mathbb{E}_{\mathbb{P}_{1}} [ \exp (D_{0}^{m,\mathrm{r}}) D_{0}^{m,\mathrm{r}}] / \mathbb{E}_{ \mathbb{P}_{1}} [ \exp (D_{0}^{m,\mathrm{r}})]\) for all \(m \in \mathbf{N}\) and obtain \(\lim_{m \to \infty }\mathbb{E}_{\mathbb{Q} _{0}^{m,\mathrm{r}}} [ D_{0}^{m,\mathrm{r}}] = 0\), which contradicts the fact that \(\mathbb{E}_{\mathbb{Q}_{0}^{m,\mathrm{r}}} [ D_{0}^{m, \mathrm{r}}]=1\) for all \(m \in \mathbf{N}\). We conclude that \((z_{0}^{m,\mathrm{r}})_{m \in \mathbf{N}}\) is also bounded from below.
To show (A.19), note that \(w^{m}(x) \leq \lambda_{0}^{m} \delta_{1} \log x\) for \(0 < x \leq 1\); hence, \(\log D_{0}^{m, \mathrm{r}}\geq (z_{0}^{m,\mathrm{r}}+ C^{m, \ast }_{0})/ (\lambda _{0}^{m} \delta_{1})\) on \(\{D_{0}^{m,\mathrm{r}}\leq 1\}\) for all \(m \in \mathbf{N}\). From (A.18), we obtain that for all \(m \in \mathbf{N}\),
The right-hand side of this inequality is bounded in \(\mathbf{R}\); therefore, (A.19) follows. Similarly, since \(\lambda_{0}^{m} \delta_{1} \log x \leq w^{m}(x)\) for \(x > 1\), we obtain for all \(m \in \mathbf{N}\) that \(\log D_{0}^{m,\mathrm{r}}\leq (z_{0}^{m, \mathrm{r}}+ C^{m, \ast }_{0})/ (\lambda_{0}^{m} \delta_{1})\) on \(\{D_{0}^{m,\mathrm{r}}> 1\}\). Using the same estimates from (A.18) that were used to establish (A.19), (A.20) follows. □
Lemma A.6
Take \(z^{\infty , \diamond }_{0}\) as in Lemma 5.3. If \((z^{m_{k}, \diamond }_{0})_{k \in \mathbf{N}}\) is any convergent subsequence of \((z^{m, \diamond }_{0})_{m \in \mathbf{N}}\), then \(\lim_{k \to \infty } z^{m_{k}, \diamond }_{0} {=} z^{\infty , \diamond }_{0}\) and \(\mathbb{L}^{0} \mbox{-} \lim_{k \to \infty } C^{m _{k}, \diamond }_{0} {=} C^{\infty }_{0} (z^{\infty , \diamond }_{0})\). Similarly, we have \(\lim_{k \to \infty }z_{0}^{m_{k},\mathrm{r}}= z ^{\infty , \diamond }_{0}\) and \(\mathbb{L}^{0} \mbox{-} \lim_{k \to \infty }C_{0}^{m_{k},\mathrm{r}}= C^{\infty }_{0}(z^{ \infty , \diamond }_{0})\) whenever \((z_{0}^{m_{k},\mathrm{r}})_{k \in \mathbf{N}}\) is a convergent subsequence of \((z_{0}^{m,\mathrm{r}})_{m \in \mathbf{N}}\).
Proof
Set \(\widehat{z}_{0}^{\infty }\mathrel{\mathop{:}}=\lim_{k \to \infty }z^{m_{k}, \diamond }_{0}\) and \(\widetilde{z}_{0}^{\infty }\mathrel{ \mathop{:}}=\lim_{k \to \infty }z_{0}^{m_{k},\mathrm{r}}\). Define the function \((0, \infty ) \ni x \mapsto \phi (x) = \delta_{1} (x - 1) + \delta_{1} \log x\) and note that both \((\phi^{m})_{m \in \mathbf{N}}\) of (A.15) and \((w^{m})_{m \in \mathbf{N}}\) of (A.14) converge uniformly to \(\phi \) on compact subsets of \((0, \infty )\). This fact, combined with (A.16) and Lemmas A.4 and A.5, implies that \((D^{m_{k}, \diamond }_{0})_{k \in \mathbf{N}}\) has a \((0, \infty )\)-valued \(\mathbb{L}^{0}\)-limit \(\widehat{D}^{\infty }_{0}= 1 + \widehat{C}^{\infty }_{0}/ \delta_{1}\) and \((D_{0}^{m_{k}, \mathrm{r}})_{k \in \mathbf{N}}\) has a \((0, \infty )\)-valued \(\mathbb{L}^{0}\)-limit \(\widetilde{D}^{\infty }_{0} = 1 + \widetilde{C}^{\infty }_{0} / \delta_{1}\), satisfying \(\phi ( \widehat{D}^{\infty }_{0}) = \widehat{z}_{0}^{\infty }+C^{\infty , \ast }_{0}\) and \(\phi (\widetilde{D}^{\infty }_{0}) = \widetilde{z} _{0}^{\infty }+ C^{\infty , \ast }_{0}\).
We first tackle the Nash equilibrium case. In the proof of Lemma A.4, the equality
was established. Since \(\lim_{k \to \infty }\delta^{m_{k}}_{0} = \infty \) and \(\exp (- \delta_{1} D^{m_{k}, \diamond }_{0} / \delta ^{m_{k}}_{0} ) \leq 1\) for all \(k \in \mathbf{N}\), (A.17) allows us to use the dominated convergence theorem to obtain
Lemma 5.3 then yields \(\widehat{z}_{0}^{\infty }= z^{ \infty , \diamond }_{0}\), which also implies \(\widehat{C}^{\infty } _{0}= C^{\infty , \diamond }_{0} (z^{\infty , \diamond }_{0})\).
We continue to deal with the best response case. Since (3.5) implies that
we obtain
By the domination relationship in (A.19), we may apply the dominated convergence theorem in the numerator to obtain
Similarly, the domination relationship in (A.19) allows us to apply the dominated convergence theorem in the denominator to obtain
Combining everything, we obtain \(\mathbb{E}_{\mathbb{P}_{0}} [ 1/ \widetilde{D}^{\infty }_{0} ] = 1\), and by Lemma 5.3, it follows that \(\widetilde{z}_{0}^{\infty } {=} z^{\infty , \diamond }_{0}\) and \(\widetilde{D}^{\infty }_{0} {=} 1 {+} C_{0}^{\infty }(z^{\infty , \diamond }_{0})/\delta_{0}\), which in turn implies \(\widetilde{C}_{0} ^{\infty } {=} C_{0}^{\infty }(z^{\infty , \diamond }_{0})\). □
We may now conclude the proof of Theorem 5.4. By way of contradiction, if \(\mathbb{L}^{0} \mbox{-} \lim_{m \to \infty }C^{m, \diamond }_{0} = C_{0}^{\infty }(z^{\infty , \diamond } _{0})\) fails, there exist \(\epsilon \in (0, 1)\) and a subsequence \((C^{m_{k}, \diamond }_{0})_{k \in \mathbf{N}}\) of \((C^{m, \diamond })_{m \in \mathbf{N}}\) such that \(\mathbb{E}[1 \wedge |C_{0} ^{m_{k},\mathrm{r}}- C_{0}^{\infty }(z^{\infty , \diamond }_{0})|] > \epsilon \) for all \(k \in \mathbf{N}\). Since the sequence \((z^{m_{k}, \diamond }_{0})_{k \in \mathbf{N}}\) is bounded by Lemma A.4, there exists a further subsequence of \((z^{m_{k}, \diamond }_{0})_{k \in \mathbf{N}}\) that is convergent. Then Lemma A.6 implies that there exists a further subsequence of \((C^{m_{k}, \diamond }_{0})_{k \in \mathbf{N}}\) that \(\mathbb{L}^{0}\)-converges to \(C_{0}^{\infty }(z^{\infty , \diamond } _{0})\), contradicting the fact that \(\mathbb{E}[1 \wedge |C^{m_{k}, \diamond }_{0} - C_{0}^{\infty }(z^{\infty , \diamond }_{0})|] > \epsilon \) for all \(k \in \mathbf{N}\). The proof that \(\mathbb{L}^{0} \mbox{-} \lim_{m \to \infty }C_{0}^{m,\mathrm{r}}= C_{0}^{\infty }(z ^{\infty , \diamond }_{0})\) is carried out in the exact same way, using Lemma A.5 in place of Lemma A.4. □
1.10 A.10 Proof of Proposition 5.5
Recall that \(u^{m, \diamond }_{0} = - \delta^{m}_{0} \log \mathbb{E} _{\mathbb{P}_{0}} [\exp (- C^{m, \diamond }_{0} / \delta_{0}^{m})]\) for all \(m \in \mathbf{N}\). On the one hand, \(u^{m, \diamond }_{0} \leq \mathbb{E}_{\mathbb{P}_{0}} [C^{m, \diamond }_{0}]\) for all \(m \in \mathbf{N}\). From (4.4) and (A.16), we get that on the event \(\{C^{m, \diamond }_{0} > 0\}\), we have \(C^{m, \diamond }_{0} \leq z^{m, \diamond }_{0} + C^{m, \ast }_{0}\) for all \(m \in \mathbf{N}\). Therefore, by (A.18), Lemma A.4 and Proposition 5.2, there exists a constant \(k > 0\) such that \(C^{m, \diamond }_{0} \leq k + \log^{+} (\mathrm{d}\mathbb{P} _{0} / \mathrm{d}\mathbb{P}_{1})\) for all \(m \in \mathbf{N}\). By Assumption 5.1 and (the reverse version of) Fatou’s lemma, it follows that \(\limsup_{m \to \infty } u^{m, \diamond }_{0} \leq \mathbb{E}_{\mathbb{P}_{0}} [C^{\infty , \diamond }_{0}]\). On the other hand, since \(\lim_{m \to \infty }\delta_{0}^{m} = \infty \), it follows for all \(k \in \mathbf{N}\) that
where the last equality follows from the dominated convergence theorem, and where the fact that \(- C^{m, \diamond }_{0} \leq \delta_{1}\) for all \(m \in \mathbf{N}\) is also used. Sending \(k \to \infty \), we get \(\liminf_{m \to \infty } u^{m, \diamond }_{0} \geq \lim_{k \to \infty } (- k \log \mathbb{E}_{\mathbb{P}_{0}}[\exp (- C^{\infty , \diamond }_{0} / k)]) = \mathbb{E}_{\mathbb{P}_{0}} [C^{\infty , \diamond } _{0}]\). Combining this with the inequality \(\limsup_{m \to \infty } u ^{m, \diamond }_{0} \leq \mathbb{E}_{\mathbb{P}_{0}} [C^{\infty , \diamond }_{0}]\), we obtain
Since \(\lim_{m \to \infty } u^{m, \ast }_{0} = 0\), \(\lim_{m \to \infty } (u^{m, \diamond }_{0} - u^{m, \ast }_{0}) = (1 / \delta_{1}) \mathrm{Var}_{\mathbb{Q}^{\infty , \diamond }} (C^{\infty , \diamond }_{0})\) follows. To obtain the limiting utility loss for agent 1, taking expectations with respect to \(\mathbb{P}_{0}\) in the equality \(C^{\infty , \diamond }_{0} + \delta_{1} \log (1 + C^{\infty , \diamond }/ \delta_{1}) = z^{\infty , \diamond }_{0} + C^{\infty , \ast }_{0}\), we obtain \(\mathbb{E}_{\mathbb{P}_{0}} [C^{\infty , \diamond }_{0}] + \delta_{1} \mathbb{E}_{\mathbb{P}_{0}} [\log (\mathrm{d} \mathbb{P}_{0} / \mathrm{d}\mathbb{Q}^{\infty , \diamond })] = z^{ \infty , \diamond }_{0}\), where we used the fact that \(1 + C ^{\infty , \diamond }_{0} / \delta_{1} = \mathrm{d}\mathbb{P}_{0} / \mathrm{d}\mathbb{Q}^{\infty , \diamond }\). Recalling \(\mathbb{E} _{\mathbb{P}_{0}} [C^{\infty , \diamond }_{0}] = (1 / \delta_{1}) \mathrm{Var}_{\mathbb{Q}^{\infty , \diamond }} (C^{\infty , \diamond }_{0})\), we obtain \(z^{\infty , \diamond }_{0} = (1 / \delta_{1}) \mathrm{Var}_{\mathbb{Q}^{\infty , \diamond }} (C^{\infty , \diamond }_{0}) + \delta_{1} \mathcal{H}(\mathbb{P}_{0} \, | \,\mathbb{Q}^{ \infty , \diamond })\). In particular, since \(z^{\infty , \diamond }_{0} \in \mathbf{R}_{+}\), it follows that \(\mathrm{Var} _{\mathbb{Q}^{\infty , \diamond }} (C^{\infty , \diamond }_{0}) < \infty \) and \(\mathcal{H}(\mathbb{P}_{0} \, | \,\mathbb{Q}^{\infty , \diamond }) < \infty \). Now recall that \(\lim_{m \to \infty }z ^{m, \diamond }_{0} = z^{\infty , \diamond }_{0}\) was obtained in the proof of Theorem 5.4 and that from (4.9),
Since \(\lim_{m \to \infty }(u^{m, \ast }_{0} - u^{m, \diamond }_{0}) = (1 / \delta_{1})\mathrm{Var}_{\mathbb{Q}^{\infty , \diamond }} (C^{ \infty , \diamond }_{0}) < \infty \), \(\lim_{m \to \infty }\lambda_{0} ^{m} = 1\) and \(\lim_{m \to \infty }\lambda_{1}^{m} = 0\), it follows that
which concludes the proof. □
1.11 A.11 Proof of Theorem 5.7
Under Assumption 5.6, we have \(\delta_{0}^{m} \log (\mathrm{d}\mathbb{P}_{0}^{m} / \mathrm{d}\mathbb{Q}^{m, \ast }) \sim \lambda_{1} \xi_{0} - \lambda_{0} \xi_{1}\) for all \(m \in \mathbf{N}\); therefore, \(C^{m, \ast }_{0} = \lambda_{1} \xi_{0} - \lambda_{0} \xi_{1} - \mathbb{E}_{\mathbb{Q}^{m, \ast }} [\lambda_{1} \xi_{0} - \lambda_{0} \xi_{1}]\) for all \(m \in \mathbf{N}\). Because \(( \lambda_{1} \xi_{0} - \lambda_{0} \xi_{1}) \in \mathbb{L}^{\infty }\) and \((\mathbb{Q}^{m, \ast })_{m \in \mathbf{N}}\) converges to ℙ in the total-variation norm, we readily obtain \(\lim_{m \to \infty }\mathbb{E}_{\mathbb{Q}^{m, \ast }} [\lambda_{1} \xi_{0} - \lambda_{0} \xi_{1}] = \mathbb{E}_{\mathbb{P}} [\lambda_{1} \xi_{0} - \lambda_{0} \xi_{1}] = 0\); therefore, \(\lim_{m \to \infty }C^{m, \ast }_{0} = \lambda_{1} \xi_{0} - \lambda_{0} \xi_{1}\) follows.
We proceed with the limiting behaviour of the sequence \((C^{m, \diamond })_{m \in \mathbf{N}}\). For each \(m \in \mathbf{N}\), define the function
It then follows by (A.13) that \(\psi^{m} (C^{m, \diamond } _{0}) = z^{m, \diamond }_{0} + C^{m, \ast }_{0}\) for all \(m \in \mathbf{N}\). Note that \(\psi^{m}\) is strictly increasing with \(\psi^{m}(0) = 0\) for all \(m \in \mathbf{N}\); furthermore, \((\psi^{m})_{m \in \mathbf{N}}\) converges uniformly on compact subsets of \(\mathbf{R}\) to \(\psi^{\infty }: \mathbf{R}\to \mathbf{R}\) defined by \(\psi^{\infty }(y) = 2 y\).
Lemma A.7
The sequence \((z^{m, \diamond }_{0})_{m \in \mathbf{N}}\) is bounded in \(\mathbf{R}\).
Proof
We show that \((z^{m, \diamond }_{0})_{m \in \mathbf{N}}\) is bounded above. A symmetric argument applied to agent 1 shows that \((z^{m, \diamond }_{1})_{m \in \mathbf{N}}\) is bounded above; since \(z^{m, \diamond }_{0} = - z^{m, \diamond }_{1}\) for all \(m \in \mathbf{N}\), it follows that \((z^{m, \diamond }_{0})_{m \in \mathbf{N}}\) is also bounded below.
Recall that \(\mathbb{E}_{\mathbb{Q}^{m, \diamond }} [C^{m, \diamond } _{0}] = 0\) for all \(m \in \mathbf{N}\). As in the beginning of the proof of Lemma A.4, applying (4.2) for \(i=1\) and using (4.3), we have
for all \(m \in \mathbf{N}\). Therefore, for every \(m \in \mathbf{N}\),
where the last inequality follows from
We obtain then that \(\mathbb{E}_{\mathbb{P}} [\exp ( \xi_{1} / \delta ^{m}_{1}) C^{m, \diamond }_{0}] \leq 0\) for all \(m \in \mathbf{N}\).
Suppose that \((z^{m, \diamond }_{0})_{m \in \mathbf{N}}\) fails to be bounded above. By passing to a subsequence if necessary, we may assume that \((z^{m, \diamond }_{0})_{m \in \mathbf{N}}\) is a sequence of nonnegative numbers with \(\lim_{m \to \infty }z^{m, \diamond }_{0} = \infty \). By (A.13), it then follows that \(\lim_{m \to \infty }\mathbb{P}[C^{m, \diamond }_{0} > K] = 1\) for all \(K \in \mathbf{R}_{+}\). Furthermore, \(C^{m, \diamond }_{0} \geq - (C^{m, \ast }_{0})^{-}\) for all \(m \in \mathbf{N}\), which, together with the uniform boundedness of \((C^{m, \ast }_{0})_{m \in \mathbf{N}}\), implies the existence of \(c_{0} \in (0, \infty )\) such that \(C^{m, \diamond } _{0} \geq - c_{0}\) for all \(m \in \mathbf{N}\). Since \(\xi_{1} \in \mathbb{L}^{\infty }\), \(\exp ( \xi_{1} / \delta^{m}_{1}) C^{m, \diamond }_{0} \geq - c\) for all \(m \in \mathbf{N}\) and an appropriate \(c \in (0, \infty )\). The last domination from below, combined with \(\mathbb{L}^{0} \mbox{-} \lim_{m \to \infty }\exp ( \xi_{1} / \delta ^{m}_{1}) = 1\) and \(\lim_{m \to \infty }\mathbb{P}[C^{m, \diamond } _{0} > K] = 1\) for all \(K \in \mathbf{R}_{+}\), implies \(\lim_{m \to \infty }\mathbb{E}_{\mathbb{P}} [\exp ( \xi_{1} / \delta ^{m}_{1}) C^{m, \diamond }_{0}] = \infty \), which contradicts the fact that \(\mathbb{E}_{\mathbb{P}} [\exp ( \xi_{1} / \delta^{m}_{1}) C^{m, \diamond }_{0}] \leq 0\) for all \(m \in \mathbf{N}\). It follows that \((z^{m, \diamond }_{0})_{m \in \mathbf{N}}\) is bounded above, which completes the argument. □
Lemma A.8
Let \((z^{m_{k}, \diamond })_{k \in \mathbf{N}}\) be any convergent subsequence of \((z^{m, \diamond })_{m \in \mathbf{N}}\). Then we have \(\lim_{k \to \infty }z^{m_{k}, \diamond }=0\) and \(\mathbb{L}^{0} \mbox{-} \lim_{k \to \infty }C^{m_{k}, \diamond }_{0} = C^{\infty , \ast }_{0} /2\).
Proof
Let \(\widetilde{z}^{\infty }\mathrel{\mathop{:}}=\lim_{k \to \infty }z ^{m_{k}, \diamond }\). Due to the fact that \((\psi^{m})_{m \in \mathbf{N}}\) converges uniformly to \(\psi \) on compact subsets of \(\mathbf{R}\) and Lemma A.7, it follows that \((C^{m_{k}, \diamond }_{0})_{k \in \mathbf{N}}\) has an \(\mathbb{L} ^{0}\)-limit \(\widetilde{C}^{\infty }_{0}\), and this limit satisfies the equation \(2 \widetilde{C}^{\infty }_{0} = \widetilde{z}^{\infty }+ C ^{\infty , \ast }_{0}\). Recall the inequality \(\mathbb{E}_{\mathbb{P}} [\exp ( \xi_{1} / \delta^{m_{k}}_{1}) C^{m_{k}, \diamond }_{0}] \leq 0\) for all \(k \in \mathbf{N}\), which was established in the proof of Lemma A.7. Furthermore, since \((z^{m_{k}, \diamond })_{k \in \mathbf{N}}\) and \((C^{m_{k}, \ast }_{0})_{k \in \mathbf{N}}\) are convergent and in particular uniformly bounded from below (for the latter sequence of random variables, this follows from the fact that \(\xi_{i} \in \mathbb{L}^{\infty }\) for \(i \in \{0,1\}\)) and \(\xi_{1} \in \mathbb{L}^{\infty }\), we infer the existence of \(c \in (0, \infty )\) such that the uniform lower domination \(\exp ( \xi_{1} / \delta^{m_{k}}_{1}) C^{m_{k}, \diamond }_{0} \geq - c\) is valid for all \(k \in \mathbf{N}\). An application of Fatou’s lemma gives \(\mathbb{E}_{\mathbb{P}} [ \widetilde{C}^{\infty }_{0} ] \leq 0\). The symmetric argument from the side of agent 1 gives \(\mathbb{E}_{ \mathbb{P}} [ \widetilde{C}^{\infty }_{0} ] \geq 0\), which implies that \(\mathbb{E}_{\mathbb{P}} [ \widetilde{C}^{\infty }_{0} ] = 0\). Since \(2 \widetilde{C}^{\infty }_{0} = \widetilde{z}^{\infty }+ C^{\infty , \ast }\) and \(\mathbb{E}_{\mathbb{P}} [C^{\infty , \ast }] = 0\), it follows that \(\widetilde{z}^{\infty }= 0\). We conclude that \(\widetilde{C}^{\infty }_{0} = C^{\infty , \ast }_{0}/2\). □
The proof of Theorem 5.7 can now be completed exactly as in the case of Theorem 5.4. If \(\mathbb{L}^{0} \mbox{-} \lim_{m \to \infty }C^{m, \diamond }_{0} = C^{\infty , \ast }_{0} / 2\) were not true, then there would exist some \(\epsilon \in (0, 1)\) and a subsequence \((C^{m_{k}, \diamond }_{0})_{k \in \mathbf{N}}\) of \((C^{m, \diamond }_{0})_{m \in \mathbf{N}}\) such that \(\mathbb{E}[1 \wedge |C^{m_{k}, \diamond }_{0} - C^{\infty , \ast }_{0} / 2|] > \epsilon \) for all \(k \in \mathbf{N}\). Since the sequence \((z^{m_{k}, \diamond })_{k \in \mathbf{N}}\) is bounded due to Lemma A.7, there exists a further subsequence of \((z^{m_{k}, \diamond })_{k \in \mathbf{N}}\) that is convergent. Then Lemma A.8 implies that there exists a further subsequence of \((C^{m_{k}, \diamond }_{0})_{k \in \mathbf{N}}\) that \(\mathbb{L}^{0}\)-converges to \(C^{\infty , \ast }_{0} / 2\), contradicting \(\mathbb{E}[1 \wedge |C^{m_{k}, \diamond }_{0} - C^{ \infty , \ast }_{0} / 2|] > \epsilon \) for all \(k \in \mathbf{N}\). □
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Anthropelos, M., Kardaras, C. Equilibrium in risk-sharing games. Finance Stoch 21, 815–865 (2017). https://doi.org/10.1007/s00780-017-0323-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00780-017-0323-9