New procedure for the analysis of speed trial results, with special attention to the correction of tidal current effect

Abstract

Almost all the existing analysis methods of speed trial results were proposed before 1970s, and the actual analysis procedures are very old-fashioned with instructions like “plot the results on a chart and draw a smooth mean line”, “read a value from the mean line” and so on. Such instructions not only show up the analysis procedures old-fashioned, but also make them very ambiguous and unclear. They should be up-dated to a method which is clear not only in logic but also in calculation procedure, and also fits the present computing technology. At first, the author reviewed the major analysis methods and concluded that the logic of the up-dated analysis procedure can be composed of the logics of the existing ones. Then, the analysis procedure is composed of three stages; namely (1) correction of power and propeller revolution to the ones corresponding to no air condition, (2) correction of tidal current effect, and (3) correction of power and propeller revolution to the ones corresponding to no wind condition. For the stages (1) and (3), there seems to be no big issue except the estimation of the amount of environmentally added resistance in the stage (1). Then, the author focused on the correction of tidal current effect in this paper. For the correction of tidal current effect, the author considers the essential points for the up-date are in the direction of finding out appropriate functions for the variation of tidal current velocity and the ship speed through the water. Then, he investigated to find out such functions and made his proposal. Finally, the applicability of the new procedure is assessed by the analysis of simulated speed trial results of a VLCC.

1 Introduction

For the analysis of speed trial results of ships, many proposals have been made. Among them, the so-called “mean of means method” [1] seems to be popular in the western world, and “Taniguchi–Tamura’s method” [2] has been successfully used especially in the Far East, and was developed into an international standard of this kind [3]. However, most of the methods were presented before 1970s, and the actual analysis procedures are very old-fashioned. At the time of their proposals, computer was not commonly used and analysis calculation was performed only by slide rules, numerical tables, drawing and reading charts and so on. The author considers it is the main reason why some people feel doubtful on the effectiveness of the international standard [3] and improvement proposals were discussed in ITTC and ISO. Therefore, up-dating is certainly inevitable.

In the circumstance, the author at first tried to clarify the essential purpose of the speed trial analysis and reviewed some of the existing analysis procedures. Based on the result, he identified the most controversial part should be the part of correction of tidal current effect, and the correction is very difficult in the cases of low speed full ships. In this paper, the author presented his proposal of up-dating, following some investigations.

Strasser et al. [4] presented the summary of the investigations carried out in ITTC and ISO through which the revised international standard [5] was formulated. Basic concept of the iterative method being discussed in the paper was proposed by the author [6, 7].

Because this paper mainly deals with the correction of tidal current effect, the examples of analysed results only show the corrections from measured results to the ones in no air condition and then to the ones in no air nor current condition. The final results in this paper must be converted to those in no wind condition, however, they are not shown in this paper.

2 Overview of speed trial analysis

2.1 Purpose of the speed trial and the analysis

The purpose of speed trial is to estimate the relation among V _W, P _B and N _P in no wind condition, which corresponds to the performance of ship to be discussed between ship owner and shipyards and so on. However, we can Queryonly measure V _G ¹ in a condition sometimes far from no wind condition.

By use of the present technology, it would not be difficult to measure V _W with practical accuracy. For example, acoustic Doppler current profiler (ADCP) can measure three dimensional velocity field of water with practically sufficient accuracy. However, we have to consider, if we pursue a procedure applicable everywhere in the world; usual ships never equip such sophisticated instrument, nor it is not easy to fit the instrument temporarily for the speed trial. It is the main reason why we have to obtain the value of V _W through the analyses of the measured V _G, and the correction of tidal current effect is so important.

Although it is recommended that trial site should be selected free from environmental effect as far as possible, the ship still suffers from the effect of added resistance caused by wind and waves etc. and also the effect of tidal current.

Most of the environmental effects such as wind, waves, transverse current and so on are considered to affect the trial results through the increase of ship resistance, while component of current in ship’s longitudinal direction does not increase ship resistance, but it makes V _G different from V _W. Therefore, the analysis of speed trial results consists of the corrections of the effect of added resistance and current in longitudinal direction.

2.2 Existing analysis procedures of speed trial results

The classical assumption to correct the measured results for the effect of longitudinal current can be explained as follows;

• (1) The ship sails on the same course up and down with the same propeller revolution or engine output, and ship speeds over the ground V _G are measured.

• (2) Then, by taking average of two measured speeds, the effect of current can be cancelled.

However, such naive assumption is correct only when current velocity is constant. In usual cases, current velocity may change significantly in the duration which is necessary for the ship to accomplish a pair of up and down runs. This problem is further discussed later in the next section.

Another problem is that even if up and down runs are performed with the same propeller revolution, the resultant propeller revolutions after the correction of added resistance may not be the same any more. It is because propeller revolution, or required horse power, will decrease when a positive value of environmentally added resistance is extracted, and because the values of added resistance in up and down runs are different.

So, the problem is not easy and several of rather complicated procedures were proposed to solve it. In the followings, historical review of the development of the analysis procedures of speed trial results is presented.

2.2.1 Mean of means method

The author could not find the original description of the so-called “mean of means method”. It seems to be proposed well before 1930 for the correction of current effect. The formulation is mathematically very neat and adopted in the part of tidal current correction of the Sea Trial Code (SNAME 1973).

The summary is as follows [1]; “the speeds corrected for wind effect are still influenced by the current existing over the trial course during the runs. This current effect is eliminated as far as possible by taking ‘mean of means’ of the three runs on the measured mile at the same RPM but in different directions,

$$V_{\text{W}} = \, (V_{1} + 2 \cdot V_{2} + V_{3} )/4$$

(2.1)

this method of weighing gives the correct ship speed only if the speed of tide is varying uniformly with time. Similarly, the mean of two runs will give the correct speed only if the tide is constant, while that of four runs,

$$V_{\text{W}} = { (}V_{1} + 3 \cdot V_{2} + 3 \cdot V_{3} + V_{4} )/8$$

(2.2)

will be correct only if the tide speed is varying parabolically with time.”

The statement can easily be proved under the assumption that ship makes up and down runs with the same engine output under no environmental effect except current and that intervals of these runs are all the same. However, it is very difficult to carry out a series of trial runs which satisfies the above conditions correctly, and the effects of the dissatisfactions on the analysed results are left unclear. Then, practical investigations are necessary.

In the followings, the author tries to check the effect of tidal current. As explained in Sect. 5.1, tidal current velocity in most cases varies harmonically, with the principal lunar semidiurnal period T _Tide. In the case, current velocity can be expressed as follows;

$$\begin{aligned} V_{\text{C}} (t) & = V_{\text{C,0}} + V_{\text{C,C}} \cdot \cos \left( {\frac{2\pi }{{\text{T}_{\text{Tide}} }} \cdot t} \right) + V_{\text{C,S}} \cdot \sin \left( {\frac{2\pi }{{\text{T}_{\text{Tide}} }} \cdot t} \right) \\ & = V_{\text{C,0}} + V_{\text{C,A}} \cdot \sin \left( {\frac{2\pi }{{\text{T}_{\text{Tide}} }} \cdot t + \varepsilon } \right) \\ \end{aligned}$$

(2.3)

How accurate the analysed results are in this case?

When V _W is written as V _W,0 which should be the same for all runs, and interval of any two consecutive runs is written 2·ΔT, V _G of four runs (V _G1, V _G2, V _G3, V _G4) can be written as follows;

$$\begin{aligned} V_{{{\text{G}}, 1}} & = \, V_{\text{W,0}} + \, V_{{{\text{C}},{\text{A}}}} \cdot { \sin }(\varphi - 6\pi \cdot {\Delta\text{T}}/\text{T}_{\text{Tide}} ) \, + \, V_{{{\text{C}},0}} , \\ V_{{{\text{G}}, 2}} & = \, V_{\text{W,0}} - \, V_{{{\text{C}},{\text{A}}}} \cdot { \sin }(\varphi - 2\pi \cdot {\Delta\text{T}}/\text{T}_{\text{Tide}} ) \, - \, V_{{{\text{C}},0}} , \\ V_{{{\text{G}}, 3}} & = \, V_{\text{W,0}} + \, V_{{{\text{C}},{\text{A}}}} \cdot { \sin }(\varphi + 2\pi \cdot {\Delta\text{T}}/\text{T}_{\text{Tide}} ) \, + \, V_{{{\text{C}},0}} , \\ V_{{{\text{G}}, 4}} & = \, V_{\text{W,0}} - \, V_{{{\text{C}},{\text{A}}}} \cdot { \sin }(\varphi + 6\pi \cdot {\Delta\text{T}}/\text{T}_{\text{Tide}} ) \, - \, V_{{{\text{C}},0}} \\ \end{aligned}$$

(2.4)

where, φ: the value of (2π·t/T _Tide + ε) at the mid time of the four runs.

From them, the estimated V _W,0 by mean of means (V _W,M) is derived as

$$\begin{aligned} V_{{{\text{W}},{\text{M}}}} & = (V_{{{\text{G}}, 1}} + 3\cdot V_{{{\text{G}}, 2}} + 3\cdot V_{{{\text{G}}, 3}} + V_{{{\text{G}}, 4}} )/ 8\\ & = V_{\text{W,0}} + \, V_{{{\text{C}},{\text{A}}}} \cdot \{ \sin (\varphi - 6\pi \cdot {\Delta\text{T}}/\text{T}_{\text{Tide}} ) \\ & \quad -\sin (\varphi + 6\pi \cdot {\Delta\text{T}}/\text{T}_{\text{Tide}} )\} / 8 - 3\cdot V_{{{\text{C}},{\text{A}}}} \cdot \{\sin(\varphi - 2\pi \cdot {\Delta\text{T}}/\text{T}_{\text{Tide}} ) \\ & \quad - \sin (\varphi + 2\pi \cdot {\Delta\text{T}}/\text{T}_{\text{Tide}} )\} / 8 \end{aligned}$$

(2.5)

Then, we obtain the following result;

$$\begin{aligned} & (V_{{{\text{W}},{\text{M}}}} - \, V_{\text{W,0}} )/V_{{{\text{C}},{\text{A}}}} \\ & \quad = \, \{ { \sin }(\varphi - 6\pi \cdot {\Delta\text{T}}/\text{T}_{\text{Tide}} ) \, - { \sin }(\varphi + 6\pi \cdot {\Delta\text{T}}/\text{T}_{\text{Tide}} )\} / 8\\ & \quad \quad - 3\cdot \{ { \sin }(\varphi - 2\pi \cdot {\Delta\text{T}}/\text{T}_{\text{Tide}} ) \, - { \sin }(\varphi + 2\pi \cdot {\Delta\text{T}}/\text{T}_{\text{Tide}} )\} / 8\\ & \quad = { \cos }(\varphi) \cdot \{ 3\cdot { \sin }( 2\pi \cdot {\Delta\text{T}}/\text{T}_{\text{Tide}} ) \, - { \sin }( 6\pi \cdot {\Delta\text{T}}/\text{T}_{\text{Tide}} )\} / 4\\ & \quad = - { \cos }(\varphi) \cdot { \sin }^{ 3} ( 2\pi \cdot {\Delta\text{T}}/\text{T}_{\text{Tide}} ) \\ \end{aligned}$$

(2.6)

Likewise, for the cases of two and three runs,

$$\begin{aligned} (V_{{{\text{W}},{\text{M}}}} - \, V_{\text{W,0}} )/V_{{{\text{C}},{\text{A}}}} & = \, - { \cos }(\varphi) \cdot { \sin }( 2\pi \cdot {\Delta\text{T}}/\text{T}_{\text{Tide}} ) [{\text{two runs}}] \\ \end{aligned}$$

(2.7)

$$\begin{aligned} (V_{{{\text{W}},{\text{M}}}} - \, V_{\text{W,0}} )/V_{{{\text{C}},{\text{A}}}} & = \, - { \sin }(\varphi) \cdot { \sin }^{ 2} ( 2\pi \cdot {\Delta\text{T}}/\text{T}_{\text{Tide}} ) [{\text{three runs}}] \\ \end{aligned}$$

(2.8)

are obtained, respectively.

The parts of −cos(φ) and −sin(φ) can take the values from −1 to 1 depending on the relation of the time of trial execution and current variation. The remaining parts are the function of ΔT/T _Tide and written as F _i(ΔT/T _Tide) in the above, where i is the number of runs. Then, F _i (ΔT/T _Tide) for i = 2, 3, 4 are written, as follows;

$$\begin{aligned} F_{ 2} ({\Delta\text{T}}/\text{T}_{\text{Tide}} ) & = { \sin }( 2\pi \cdot {\Delta\text{T}}/\text{T}_{\text{Tide}} ) \\ F_{ 3} ({\Delta\text{T}}/\text{T}_{\text{Tide}} ) & = { \sin }^{ 2} ( 2\pi \cdot {\Delta\text{T}}/\text{T}_{\text{Tide}} ) \\ F_{ 4} ({\Delta\text{T}}/\text{T}_{\text{Tide}} ) & = { \sin }^{ 3} ( 2\pi \cdot {\Delta\text{T}}/\text{T}_{\text{Tide}} ) \\ \end{aligned}$$

(2.9)

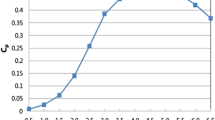
The magnitudes of F _i (ΔT/T _Tide) decide the possible amount of error of the method. The variations of F _i (ΔT/T _Tide) are calculated and shown in Fig. 1.

Fig. 1

Variation of F _i (ΔT/T _Tide) over ΔT/T _Tide

In the cases of VLCCs, time necessary for approach run well exceeds 1 h, the ratio of which to the period of tidal period (≈12 h) is more than 1/12. In Fig. 1 at ΔT/T _Tide = 1/12, the values of F _i (T/T _Tide) are 0.25 and 0.125 for three and four runs. It means that maximum absolute values of (V _W,M − V _W,0) can be 0.25 and 0.125 knot, respectively, when the amplitude of current variation V _CA is supposed 1 knot. They cannot be small enough.

2.2.2 Schoenherr’s method

Schoenherr [8] pointed out that the above “mean of means” can eliminate only the effect of current under certain conditions and that the effect of environmentally added resistance cannot be eliminated. In the paper [9], he tried to propose an approach to overcome the shortcomings. The summary is explained in the followings by use of the notation of this paper.

He proposes the use of propeller open-water characteristics for the correction of the effect of added resistance, and to correct the measured results to the values in no air condition. The reason why the correction to no air condition is desirable is explained in the Appendix.

At first, he calculates propeller torque coefficient K _Q from the measured P _B and N _P by the following formulae.

$$\begin{aligned} {P}_{\text{S}} & = {P}_{\text{B}} \cdot \eta_{\text{G}} \\ {P}_{\text{D}} & = \frac{{ {P}_{\text{S}} \cdot \eta_{\text{S}} }}{{{\text{no}} .\;{\text{of}}\;{\text{propellers}}}} \\ \end{aligned}$$

(2.10)

$$K_{\text{Q}} = \frac{{{P}_{\text{D}} \cdot \eta_{\text{R}} }}{{2\pi \cdot \rho_{\text{SW}} \cdot (N_{\text{P}} /60)^{3} \times D_{\text{P}}^{5} }}$$

(2.11)

Then, from the value of K _Q, the corresponding values of J and K _T are estimated by use of propeller open-water characteristics.

In the paper [9], only the air resistance is considered as added resistance which is estimated by the following formula.

$$R_{\text{Air}} = C_{\text{AS}} \cdot V_{\text{Wind}}^{2}$$

(2.12)

Here, C _AS is the dimensional wind resistance coefficient, and V _Wind is the relative wind velocity. He assumes the values of C _AS are the same for against and to winds.

The resistance in no air condition, which is due to water, is written as R _NA, and assumed to be the same for up and down runs. Then,

$$\begin{aligned} R_{\text{Up}} &= R_{\text{NA}} + C_{\text{AS}} \cdot V_{\text{Wind,Up}}^{2} \hfill \\ R_{\text{Down}} &= R_{\text{NA}} \pm C_{\text{AS}} \cdot V_{\text{Wind,Down}}^{ 2} \hfill \\ \end{aligned}$$

(2.13)

Lower sign in the second formula should be applied when the relative wind in down run is in the following direction. Erasing C _AS from these two equations, we can obtain R _NA as shown in the following formula.

$$R_{\text{NA}} = \frac{{R_{\text{Down}} \cdot V_{\text{Wind,Up}}^{2} \mp R_{\text{Up}} \cdot V_{\text{Wind,Down}}^{2} }}{{V_{\text{Wind,Up}}^{2} \mp V_{\text{Wind,Down}}^{2} }}$$

(2.14)

As we can suppose thrust deduction factor t being constant for a small variation of ship speed and he supposes that N _P in no air condition is not changed from the measured value, we can replace R in the formula (2.14) by K _T. Therefore, we can get K _T in no air condition as shown in the following formula.

$$K_{{{\text{T,}}N{\text{A}}}} = \frac{{K_{\text{T,Down}} \cdot V_{\text{Wind,Up}}^{2} \mp K_{\text{T,Up}} \cdot V_{\text{Wind,Down}}^{2} }}{{V_{\text{Wind,Up}}^{2} \mp V_{\text{Wind,Down}}^{2} }}$$

(2.15)

When propeller revolution is kept the same after the change of J, ship speed after the correction becomes different from the measured value. Ship speed in no air condition is obtained by the formula (2.16), on the assumptions that wake fraction is practically kept constant for a small change of J and that current speed is small in comparison with ship speed.

$$V_{\text{G,NA}} = V_{\text{G}} \cdot \frac{{J_{\text{NA}} }}{J}$$

(2.16)

From the value of K _T,NA given by (2.15), the value of J_NA and then the value of K _Q,NA can be calculated. Then, reverse application of formulae (2.10) and (2.11) will give the value of P _{B NA}, and then the whole results of trial measurement are corrected to those in no air condition.

Next is the correction for the effect of tidal current. Schoenherr points out the value of apparent slip ratio, or propeller advance coefficient J, calculated from the corrected ship speed is the indication of the tidal current, and shows an example where the time of the tidal current reversal can be found clearly by plotting apparent slip ratio on the basis of time at middle of the up and down runs. However, he does not show the procedure through which the effect of tidal current can be corrected.

Although Schoenheer’s pioneering work is highly evaluated, the author considers there are three problems.

The first one is that the values of C _AS in general are far from the same for against and to winds as shown by many wind tunnel tests results.

The second one is that the basic formula (2.13) should be corrected. In the formula, he assumes the amounts of resistance in no air condition during up and down runs are equal and writes it as R _NA. However, because up and down runs are carried out with the equivalent engine outputs and propulsion efficiency can be assumed constant when differences of ship speed and propeller loading are small, it is more likely R _Up is very close to R _Down. Because the amounts of air resistance in up and down runs would be different, the amounts of ship resistance due to water (=R _NA) are not likely the same in up and down runs.

The third one is most serious. As Schoenherr assumed propeller revolution is kept unchanged during the correction of added resistance, ship speed is changed after the correction. Because the amounts of added resistance are different between up and down runs, the variation of speed are different, and as the result, resistance due to water and therefore, propulsion power becomes different in up and down runs. It contradicts with the basic premise for the estimation of tidal current that up and down runs should be carried out with same engine power. It might be the reason why Schoenherr could not proceed to the correction of tidal current effect.

2.2.3 Taniguchi–Tamura’s method

Taniguchi and Tamura [2] developed their analysis method independently from Schoenherr’s paper [9], although their method seems to be the result of an improvement of Schoenherr’s method. They start the analysis from the correction of measured results to those in no air condition, as Schoenherr did. The method is essentially the same as Schoenherr’s method to the point where the value of K _Q is calculated from the measured results and the corresponding value of J is estimated by use of propeller open-water characteristics.

At this point, Taniguchi–Tamura considers what should be kept unchanged between measured and no air conditions, and decides to keep ship speed through the water unchanged, and propeller revolution is changed after the correction.

For the correction, non-dimensional coefficient must be selected with the denominator which is kept unchanged. Then, K _T which has propeller revolution in the denominator cannot be used, and K _T/J ², non-dimensional thrust coefficient divided by the square of propeller advance speed, is used instead. From the value of J, the corresponding value of K _T/J ² is estimated by use of propeller open-water characteristics. K _T/J ² is written as follows where the effect of resistance variation can be reflected.

$$\frac{{K_{\text{T}} }}{{J^{2} }} = \frac{T}{{\rho_{\text{SW}} \cdot V_{\text{A}}^{2} \cdot D_{\text{P}}^{2} }} = \frac{R}{{\rho_{\text{SW}} \cdot (1 - t) \cdot V_{\text{A}}^{2} \cdot D_{\text{P}}^{2} }}$$

(2.17)

In the original paper [2], only the air resistance due to wind from any relative direction is considered as added resistance which can be estimated by the following formula.

$$R_{\text{Air}} = \frac{{\rho_{\text{Air}} }}{2} \cdot C_{\text{A}} \cdot k(\alpha ) \cdot A_{\text{X}} \cdot V_{\text{Wind}}^{2}$$

(2.18)

In no air condition, resistance decreases by the amount of R _air and new value of K _T/J ² is obtained as follows, by use of V _A calculated from J and N _P and (1 − t) estimated from tank test results;

$$\frac{{K_{\text{T,NA}} }}{{J_{\text{NA}}^{2} }} = \frac{{K_{\text{T}} }}{{J^{2} }} - \frac{{R_{\text{Air}} }}{{\rho_{\text{SW}} \cdot (1 - t) \cdot V_{\text{A}}^{2} \cdot D_{\text{P}}^{2} }}$$

(2.19)

From the value of K _T,NA/J ²_NA given byThe assumption that wake fraction (2.19), the value of J _NA and then the value of K _Q,NA are calculated.

In Taniguchi–Tamura’s method, N _P in no air condition (N _P,NA) can be calculated by the following formula, because the values of V _A in measured and no air conditions are the same.

$$N_{\text{P,NA}} = N_{\text{P}} \cdot \frac{J}{{J_{\text{NA}} }}$$

(2.20)

To estimate the tidal current velocity by a half of difference of ship speeds over the ground in up and down runs, Taniguchi–Tamura must adjust the up and down propeller revolutions to the same value. To accomplish it, obtained K _Q,NA are plotted over N _P,NA on N _P − K _Q plane, the plotted points of up and down runs are moved parallel to the mean curve of N _P − K _Q relation in no air condition to the prescribed N _P (N' _P,NA), and new values of K _Q (K' _Q,NA) corresponding to N' _P,NA are obtained.

Thus, from the measured trial results, we can estimate pair of values for up and down runs with the same propeller revolution in no air condition, from which the tidal current velocity at the mid-time of the pair runs can be estimated by half of the differences of ship speed over the ground. However, ship speed over the ground at this condition cannot be the same as the measured one because propeller revolutions (N _P) of up and down runs are changed in no air condition. It must be estimated.

The difference of propeller advance speed ΔV _A, which is equal to ΔV _W·(1 − w _S), is estimated by the following formula.

$$\Delta V_{\text{A}} = (N_{\text{P,NA}}^{ '} \cdot J_{\text{NA}}^{ '} - N_{\text{P}} \cdot J) \cdot D_{\text{P}}$$

(2.21)

As ΔV _W is equal to the difference of ship speed over the ground from the measured value, we can get it if we can estimate the value of wake fraction w_S temporarily.

When we assume the average of measured values of V _G is equal to V _W, the value of wake fraction w _S,i can be estimated beforehand for the i-th pair of up and down runs by the formula (2.22) from the measured values of V _G and N _P, and the value of J corresponding to K _Q obtained by the formula (2.11). The assumption that wake fraction is practically kept constant for the small change of J is applied here.

$$1 - w_{{{\text{S}},i}} = \frac{{(N_{{{\text{P,}}i , {\text{Up}}}} \cdot J_{{i,{\text{Up}}}} + N_{{{\text{P}},i,{\text{Down}}}} \cdot J_{{i,{\text{Down}}}} )}}{{(V_{{{\text{G}},i,{\text{Up}}}} + V_{{{\text{G}},i,{\text{Down}}}} )}} \cdot D_{\text{P}}$$

(2.22)

Then, difference of ship speed through the water ΔV _W, and then new value of ship speed over the ground V' _G,NA is estimated as follows;

$$\begin{aligned} \Delta V_{\text{W}} & = (N_{\text{P,NA}}^{'} \cdot J_{\text{NA}}^{'} - N_{\text{P}} \cdot J) \cdot \frac{{D_{\text{P}} }}{{1 - w_{{{\text{S}},i}} }} \\ V_{\text{G,NA}}^{'} & = V_{\text{G}} + \Delta V_{\text{W}} \\ \end{aligned}$$

(2.23)

where J' _NA is the value of J corresponding to K' _Q,NA in propeller open-water characteristics. Now, the effect of tidal current can be corrected.

After the values of tidal current velocity are estimated for several pairs of up and down runs, a tidal current velocity curve is manually drawn. By the read values of current velocity from the curve, the values of V' _G,NA are corrected to the values of V _W. Thus, estimated tidal current velocity is correct so long as the current can be assumed to vary uniformly with time during the pair runs.

Then, as the final stage, the values of P _B and N _P are corrected to no-wind condition, where the ship performance is normally estimated.

2.2.4 BSRA standard method

BSRA standard method [10] explains that the measured results should be corrected to “no wind condition” by estimating added resistance and propulsion efficiency which is the ratio of effective power to shaft power. However, because the formula of added resistance in the method [10] contains the whole of air resistance, it is not “no wind condition” but “no air condition” to which the measured results are corrected. Therefore, up to this point, there is no essential difference in the concept, from Schoenherr’s and Taniguchi–Tamura’s methods, and in the following explanations “no wind condition” in the original document is changed to “no air condition”.

To correct the effect of tidal current on the corrected results, two kinds of charts are prepared. The first one is the plot of corrected power over the measured ship speed, where the results of up and down runs are on two different lines. On the plot, an average line of the two lines should be drawn which is supposed to be P _B and V _W relation in no air condition. The difference in abscissa (ship speed) between the average line and up or down run must be the current velocity, and the values are read from the plotted chart.

Then, in the second chart, the read values of current velocity are plotted over the time on the trial day, and a fair curve is drawn manually. The values of current velocity for the up and down runs are read from the fair curve and reflected on the first chart. And the improved line showing the relation between P _B and V _W in no air condition is obtained.

The above iteration process should be repeated until the converged results are obtained. Then, the correction of the tidal current effect is finished, and the converged results will give us the relation between P _B and V _W in no air condition.

Afterwards, the values of P _B are corrected to those in no wind condition to obtain the final results of the analysis.

3 Evaluations

To obtain data for the evaluation of the methods explained in the above, simulated speed trials are performed for a VLCC as explained in Sect. 3.1. Effectiveness of analysis methods are evaluated by examining whether the analysed results reasonably agree with the values assumed for the simulation of speed trial.

3.1 Simulated speed trials

A set of model test results, i.e. resistance and self-propulsion tests and propeller open-water test, are given for a VLCC hull form the particulars of which are shown in Table 1.

Table 1 Particulars of the VLCC

Resistance test results are analysed and the value of total resistance coefficient are fitted by the formula (3.1), and the self-propulsion factors obtained by the analysis of self-propulsion test results are approximated by first-order functions of Froude number as shown in the formula (3.2).

$$\begin{aligned} C_{\text{T}} & = (1 + k) \cdot C_{\text{F,ITTC}} + C_{\text{W}} \\ C_{\text{W}} & = a \cdot Fr^{4} + b \cdot Fr^{8} \\ \end{aligned}$$

(3.1)

$$\begin{aligned} t & = {t}_{0} + {t}_{1} \cdot Fr \\ w_{\text{m}} & = w_{{{\text{m}},0}} + w_{{{\text{m}},1}} \cdot Fr \\ \eta_{\text{R}} & = \eta_{{{\text{R}},0}} + \eta_{{{\text{R}},1}} \cdot Fr \\ \end{aligned}$$

(3.2)

where a, b, t ₀, t ₁, w _m,0, w _m,1, η _R,0, η _R,1 are appropriate coefficients.

The results of propeller open-water test are analysed and the K _T and K _Q are expressed by quadratic functions of J, respectively.

Based on such data and appropriate model-ship correlation factors, the values of P _B and N _P are estimated in still water, in both of no air and no wind conditions, when the values of V _W are given as inputs.

Simulation conditions for pseudo speed trial are set as follows; constant wind of 7 m/s is assumed to be blowing 30° from the bow. Relative wind velocity and direction are calculated from ship speed over the ground, and air resistance is estimated by the formula (2.18). The characteristics shown in Fig. 2 is used as the direction effect coefficient on wind resistance k(α), which reflects the results of wind tunnel tests performed for above water models of VLCCs.

Fig. 2

Direction effect coefficient on wind resistance

Approach distance of VLCC is assumed to be 16 sea miles, and every two runs in the speed trial are separated by the time necessary to run through twice of the approach distance. When tidal velocity variation is assumed as given by the formula (2.3), the values of V _G are set and the values of air resistance are calculated and added to resistance due to water. Then, the values of P _B and N _P are estimated.

To simulate the actual speed trial, P _B or N _P of up and down runs should be set equal. For the purpose, input values of V _W are adjusted. Thus, the results of a series of speed trial runs can be estimated by calculations. The estimated results are called “the results of simulated speed trial” in this paper, and different analysis procedures are evaluated by comparing the results of analyses with the assumed values for the simulation.

3.2 Mean of means method

As explained in Sect. 2.2.1, mean of means method is feasible for the correction of tidal current effect so long as the intervals of up and down runs are not too long in comparison with tidal variation period T _Tide. However, in the cases of low speed large full ships such as VLCCs, time interval between up and down runs must be considerably long. In such cases, the error of the analysed results can be non-negligible.

To fit the supposed condition in the mean of means method, the simulation of speed trial for this case is performed in no wind condition. Current velocity variation is assumed as shown in Fig. 3, with amplitude and mean current velocity supposed to be 0.8 and 0.2 kn, respectively.

Fig. 3

Timings of 16 runs and tidal current variation

The simulated results of 16 runs in total, two pairs of up and down runs each for four levels of engine output, are obtained where distance of approach run is assumed to be 16 sea miles. Relation between timings of the 16 runs and current velocity variation is shown in Fig. 3.

The values of cos(φ) in the formula (2.6) are calculated as −0.99, −0.14, 1.00, −0.43 for the runs of 50, 70, 85 and 100 % MCR, respectively. From the facts, it can be predicted that the values of mean of means for the runs of 50 and 85 % MCR would be somewhat far from the assumed line, and the values of mean of means for the runs of 70 and 100 % MCR would be close to the line. However, the case of 100 % MCR would be less close than the case of 70 % MCR.

In Fig. 4, the simulated trial results and the obtained values of “mean of means of V _G” (=the estimated V _W) are plotted with the corresponding values of P _B. The agreement of the values of “mean of means” with the assumed curve is as predicted.

Fig. 4

Analysed results by mean of means method

It can be understood from this example that even mean of means of four runs cannot eliminate the effect of tidal current successfully in the cases of VLCCs where time duration necessary for approach run becomes about 1 h.

3.3 Schoenherr’s and Taniguchi–Tamura’s methods

Another speed trial simulation is made in total of 8 runs in current and wind as explained in Sect. 3.1, a pair of up and down runs each for four levels of engine output, to evaluate Schoenherr’s, Taniguchi–Tamura’s and BSRA standard methods. All the methods correct the measured results to the values corresponding to no air condition.

However, there is a big difference between Schoenherr’s and Taniguchi–Tamura’s methods what sailing condition is supposed in no air condition after the value of J _NA is obtained. Schoenherr changes ship speed while keeping propeller revolution unchanged. In contrast, Taniguchi–Tamura changes propeller revolution while keeping ship speed unchanged, and after the correction, adjusts propeller revolution to the measured value for the estimation of tidal current velocity.

Figure 5 shows the comparison of the corrected results to no air condition by the two methods on N _P − K _Q plane for the simulated trial results.

Fig. 5

Comparison of the results corrected to no air condition by Schoenherr’s and Taniguchi–Tamura’s methods on N _P − K _Q plane

The corrected results for down runs by Taniguchi–Tamura’s method are all very close to the simulated trial results, because the amounts of air resistance are very small. The results by the original Schoenherr’s method shown by ● marks are obtained for pairs of up and down runs, and very close to the results of down runs in this example. It seems to mean the corrected results by Schoenherr’s and Taniguchi–Tamura’s methods are almost on one curve. However, it is only a coincidence caused by the underestimation of air resistance at against wind condition by the original Schoenherr’s formula (2.12).

When Schoenherr’s assumption that propeller revolution is kept unchanged during the correction to no air condition is applied with the value of R _Air estimated by the formula (2.18), K _T,NA can be calculated by

$$K_{\text{T,NA}} = K_{\text{T}} - \frac{{R_{\text{Air}} }}{{\rho_{\text{SW}} \cdot (1 - t) \cdot N_{\text{P}}^{ 2} \cdot D_{\text{P}}^{ 4} }}$$

(3.3)

for the results of individual runs. The values of K _Q,NA calculated from J _NA corresponding to K _T,NA are shown by △ marks in Fig. 5, which are on quite different two lines. The corrected results to no air condition by Schoenherr’s method do not result in one smooth line on N _P − K _Q plane. It shows that Schoenherr’s method contains problems as explained in Sect. 2.2.2 and should not be used.

Figure 6 shows the measured data and corrected results to no air condition by Taniguchi–Tamura’s method on N _P − K _Q plane. Although measured K _Q of up runs shown by △ are significantly bigger than those of down runs shown by ○, after the corrections, those of up and down runs shown by ▲ and ● seem to line up almost on a same curve.

Fig. 6

K _Q over N _P as measured and corrected to no air condition by Taniguchi–Tamura’s method

Taniguchi–Tamura’s method estimates the values of current velocity at mid-time of up and down runs by half of difference of ship speeds over the ground. In Fig. 7, the results of current velocity variations are shown which are obtained by the analysis of simulated speed trial results by Taniguchi–Tamura’s method. There are eight measured points corresponding to four pairs of up and down runs, and four mid-time points where values of current velocity are estimated.

Fig. 7

Current velocity estimated by Taniguchi–Tamura’s method

Marks ○ show assumed values of current velocity for the trial simulation. Marks □ show the values of current velocity estimated by half of difference of measured V _G, and marks ◇ show the estimated values in the same way after the correction to no air condition. The solid line is drawn through the points marked by ◇, and the points marked by ▲ are obtained on the curve at the time of trial runs. It is the correction process given in Taniguchi–Tamura’s method and marks ▲ give the final corrected results.

However, the solid line does not pass necessarily through the points of assumed current velocity marked by ○, especially when trial runs are carried out near the extreme values of current velocity variation. The reason is the curvature of current velocity variation line, because of which the mean point of the paired points marked by ▲ does not necessarily coincide with the corresponding point marked by ◇.

Therefore, the further correction should be made where ◇ marks are shifted by the difference, and the points marked by ◆ are obtained. Through the points marked by ◆ a dotted line is drawn, and the calculated values on the dotted line marked by × almost coincide to ○ marks. It is the only one improvement which should be made on Taniguchi–Tamura’s method.

3.4 BSRA standard method

Figure 8 shows the plot of simulated trial results of the VLCC for four levels of engine outputs corrected to no air condition by Taniguchi–Tamura’s method on V _G, V _W − P _B plane, with a thick solid line which indicates the V _W − P _B relation in no air condition assumed for trial simulation. The results from the original trial simulation, where the approach run length is assumed to be 16 sea miles, are shown by the marks □ and ■. Although the results would be usual for the speed trial of VLCCs, it is very difficult to draw a mean line of the marks because the shapes of two lines connecting □ and ■ are quite complicated.

Fig. 8

Plots on V _G, V _W − P _B plane of simulated trial results corrected to no air condition

Then, another trial simulation is made where the length of approach run is assumed to be only 4 sea miles, which is far from the reality of VLCC speed trials. The corrected results to no air condition are shown by the marks ◇ and ◆. In this case, it is easier to draw a mean line like the thick solid line in the figure.

Although the author admits the principle of the method is reasonable and easy to understand, it seems that only a skilled and well-accustomed person can deal with the analysis of speed trial results even in the latter case. He is also afraid practical execution of the analysis by the method can be very ambiguous.

3.5 Conclusions from the review and evaluations

As the results of the review and evaluations of the major speed trial analysis methods, the author concludes as follows; and the scope of the new procedure is made clear to some extent.

• (1) There is a special difficulty in the correction of tidal current effect when the trial results of low-speed very large full ships like VLCCs are dealt with. In such cases, long approach run is necessary to reach steady sailing condition, and it results in the whole duration of speed trial comparable to or even longer than the variation period of tidal current velocity.

• (2) The accuracy of the correction of tidal current effect by mean of means method is not enough in the cases of ships like VLCCs. Schoenherr’s method does not give correct results and is not complete for the correction of tidal current effect.

• (3) The principles of the analysis proposed in Taniguchi–Tamura’s method and BSRA standard method seem to be established very well. Taniguchi–Tamura’s method improved for the point specified in Sect. 3.3 and BSRA standard method would produce reasonable analysed results, if they could be used properly.

• (4) For the correction to no air condition, we have to correct the effect of added resistance in the case where only propeller torque and revolution are measured. Then, we have to estimate quasi-propulsive efficiency η _D;

  $$\eta_{\text{D}} = \frac{{P}_{\text{E}}}{{P}_{\text{D}}} = \eta_{\text{H}} \cdot \eta_{\text{O}} \cdot \eta_{\text{R}} = \frac{1 - t}{1 - w} \cdot \eta_{\text{O}} \cdot \eta_{\text{R}}$$

  (3.4)

  As the value of wake fraction w of the ship, the results obtained by model propulsion test cannot be used because of the significant Reynolds number effect, and it is supposed at present that wake fraction would be obtained by the analysis of the results of speed trial. Then, how to estimate η _D is a serious problem. However, when we employ Taniguchi–Tamura’s method, we do not need to use wake fraction of the ship explicitly. In this context, the correction method is very smart and has a big advantage.

• (5) In all methods except mean of means method, such processes like “plotting analysed data on a chart”, “manual drawing of a fair mean line”, and “reading the value on the mean line from the chart” are necessary. We have to eliminate them, not only to avoid ambiguity in the analysis procedure but also to improve the efficiency of the work.

Considering them, the author tries to propose a new procedure in the next chapter.

4 Proposal of up-to-date procedure

4.1 Summary

In this chapter, the newly proposed procedure would be summarised, and the detailed explanation on the part of the correction of tidal current effect, which is the main part to be up-dated, is presented in Sect. 5.

The author concludes that the analysis procedure should be composed of the following three stages.

• (1) Correction of power and propeller revolution to the ones corresponding to no air condition

• (2) Correction of the effect of tidal current

• (3) Correction of power and propeller revolution to the ones corresponding to no wind condition

For the stage (1), the proposed correction procedure is summarised in Sect. 4.2. The author considers there is no significant issue at this stage except how to estimate the amount of added resistance. There would be several estimation methods for each resistance component; however, the author believes the discussions on the reliability of the estimation methods are almost useless, because even a reliable method can produce a strange set of results if it is used improperly. The most important point at this stage is validity check of the corrected results and the amount of estimated added resistance. It will be discussed in Sect. 4.3.

For the stage (2) which is the main focus of this paper, the author considers serious discussions and some investigations are necessary. The correction process is summarised in Sect. 4.4. The detailed construction of the procedure and the author’s proposal with its background will be presented in Sect. 5.

For the stage (3), a correction procedure is summarised in Sect. 4.5. This stage is simple and has no complicated procedure, because the logic is the same as that of the stage (1).

4.2 Correction to no air condition

The purpose of the correction is to obtain the ship’s performance where only the resistance due to velocity through the water is acting on the ship. As the first step to accomplish it, the amounts of the added resistance components are estimated and the effects of the added resistance on P _B and N _P are corrected by use of propeller open-water characteristics and self-propulsion factors.

When Schoenherr’s and Taniguchi–Tamura’s methods were proposed, only air resistance was considered as added resistance. Later when ISO-15016 [3] was formulated, various other added resistance components were introduced, which are caused by waves, drifting, steering and so on. When various components of added resistance are estimated, total amount of added resistance R _added can be estimated as a summation.

To correct the effect of R _added, P _D and K _Q are estimated from the measured values of P _B and N _P by the formulae (2.10) and (2.11). Then, from the value of K _Q, the values of J and K _T/J ² which can be written as the formula (2.17) are estimated by use of propeller open-water characteristics.

In no air condition, resistance decreases by R _added and new value of K _T/J ² (K _T,NA/J ²_NA ) is obtained as follows;

$$\begin{aligned} \frac{{K_{\text{T,NA}} }}{{J_{\text{NA}}^{2} }} & = \frac{{R - R_{\text{Added}} }}{{\rho_{\text{SW}} \cdot (1 - t) \cdot V_{\text{A}}^{2} \cdot D_{\text{P}}^{2} }} \\ & = \frac{{K_{\text{T}} }}{{J^{2} }} - \frac{{R_{\text{Added}} }}{{\rho_{\text{SW}} \cdot (1 - t) \cdot V_{\text{A}}^{2} \cdot D_{\text{P}}^{2} }} \\ \end{aligned}$$

(4.1)

The new values of J (J _NA) and K _Q (K _Q,NA) are evaluated by use of propeller open-water characteristics, J _NA from K _T,NA/J ²_NA and then K _Q,NA from J _NA. Because V _W and therefore V _A are kept unchanged during the correction, the new value of N _P (N _P,NA) is obtained by the formula (2.20).

By the reverse application of formulae (2.10) and (2.11), the new values of P _D (P _{D ,NA}) and then P _B (P _{B ,NA}) can be calculated by the following formulae.

$${{P}_{\text{D}}}_{\text{,NA}} = \frac{{2\pi \cdot \rho_{\text{SW}} \cdot (N_{\text{P,NA}} /60)^{3} \cdot K_{\text{Q,NA}} \cdot D_{\text{P}}^{5} }}{{\eta_{\text{R}} }}$$

(4.2)

$$\begin{aligned} {{P}_{\text{S}}}_{\text{,NA}} & = \frac{{{{P}_{\text{D}}}_{\text{,NA}} \times {\text{no}} .\;{\text{of}}\;{\text{propellers}}}}{{\eta_{\text{S}} }} \\ {{P}_{\text{B}}}_{\text{,NA}} & = {{P}_{\text{S}}}_{\text{,NA}} /\eta_{\text{G}} \\ \end{aligned}$$

(4.3)

Through the process, P _B and N _P are corrected to the new values (P _{B ,NA}, N _P,NA), while the value of V _G is kept unchanged because V _W is not changed.

4.3 Validity check of the estimated added resistance

In the cases where wind and/or waves have significant effects on ship resistance, the effects usually emerge as the increase of resistance and the reduction is rare. Therefore, the overestimation of the effect usually shows the ship’s performance better. Then, the organization which tries to check the analysed results must know whether corrected results are appropriate or not.

Schoenherr [9] and Taniguchi and Tamura [2] explain that, after the correction to no air condition, K _Q values plotted over N _P values would form a fair curve. It is because the K _Q–N _P chart can be understood as a form of P _B –V _W relationship. N _P is considered as a measure of V _W because propeller slip ratio and wake fraction are expected to change only slightly, and K _Q is a non-dimensional expression of delivered power. If the effects of environmentally added resistance including air resistance are corrected properly, only the propulsive power due to ship’s advance speed through the water V _W remains. Then, K _Q must be on a fair curve over N _P. The characteristics could be used for the validity check of the corrected results.

The K _Q–N _P relation corrected to no air condition shown in Fig. 6 is obtained by assuming C _A = 0.8, which is used for the simulated speed trial. In the figure, the corrected values of K _Q and N _P of up and down runs shown by ▲ and ● marks seem to line up almost on a same curve.

However, if improper C _A is used for the correction, the results are quite different. Figure 9 shows the results when C _A = 1.0 is used for the correction. In this case, the corrected K _Q of up runs shown by ▲ are apparently too small in comparison with those of down runs shown by ●. The tendency that the measured results showing larger K _Q due to the larger environmentally added resistance are corrected to smaller K _Q, means “over correction”.

Fig. 9

K _Q over N _P as measured and corrected to no air condition (C _A = 1.0 is used for the correction)

When the corrected results in no air condition have wide scatter and it is difficult to distinguish what level is proper, the principle to follow is “The corrected result is more reliable, when the amount of correction is smaller.” The reason is simple; such data is less affected by the correction process and closer to the directly measured result.

4.4 Correction to no current condition

After the measured results of P _B and N _P are corrected to the values in no air condition, the ship is running in the vacuum with V _G, P _{B ,NA} and N _P,NA. At the condition, only resistance due to ship speed through the water V _W is acting on the ship, and P _{B ,NA} or N _P,NA is considered to be a smooth function of V _W only.

At this stage, V _W and V _C can be determined by the above assumption and another reasonable assumption that V _C is a smooth function of time of the trial day.

The author believes, for a good proposal of up-to-date version of tidal current correction procedure, it is necessary to consider at first how to express V _W and variation of V _C by simple form functions of measured items.

If we can express V _W in no air condition by a linear combination of functions of measured P _B and N _P

$$\begin{aligned} V_{\text{W}} & = A_{1} \cdot f_{1} ({{P}_{\text{B}}},N_{\text{P}} ) + A_{2} \cdot f_{2} ({{P}_{\text{B}}},N_{\text{P}} ) \\ & \quad + A_{3} \cdot f_{3} ({{P}_{\text{B}}},N_{\text{P}} ) \\ \end{aligned}$$

(4.4)

and V _C by a linear combination of functions of time,

$$V_{\text{C}} = V_{\text{C,1}} \cdot g_{1} (t) + V_{\text{C,2}} \cdot g_{2} (t) + V_{\text{C,3}} \cdot g_{3} (t)$$

(4.5)

then the measured V _G can be written as follows;

$$\begin{aligned} V_{\text{G}} & = V_{\text{W}} \pm V_{\text{C}} = A_{1} \cdot f_{1} ({{P}_{\text{B}}},N_{\text{P}} ) \\ & \quad + A_{2} \cdot f_{2} ({{P}_{\text{B}}},N_{\text{P}} ) + A_{3} \cdot f_{3} ({{P}_{\text{B}}},N_{\text{P}} ) \\ & \quad \pm V_{\text{C,1}} \cdot g_{1} (t) \pm V_{\text{C,2}} \cdot g_{2} (t) \pm V_{\text{C,3}} \cdot g_{3} (t) \\ \end{aligned}$$

(4.6)

where, double sign (±) reflects the ship’s heading.

The formula (4.6) gives us linear simultaneous equations for the unknowns A _i and V _C,i , when the measured results of up and down runs are obtained and corrected to no air condition. By solving the simultaneous equations or through iteration procedure given by BSRA standard method, and obtaining the values of the unknowns, we can evaluate the value of V _W corresponding to the values of P _B, N _P and V _C. Therefore, how to express V _W and V _C by functions of measured values is a task of vital importance.

When the concept is realised, the basic premise that a pair of up and down trial runs should be carried out with same engine output is not necessary. And complicated adjustment procedure of propeller revolution after the correction to no air condition, which is explained after the formula (2.20) to the formula (2.23), is not necessary to follow. It is a big advantage.

Investigations for the functions and detailed construction of the analysis procedure are presented in Sect. 5.

4.5 Correction to no wind condition

After the correction of tidal current effect, the values of V _W corresponding to the values of P _{B ,NA} and N _P,NA are obtained together with the estimated values of V _C. It means the ship is running in no air condition with V _W, P _{B ,NA} and N _P,NA. To obtain the final results in no wind condition, the effect of air resistance should be corrected. Air resistance in the condition can be estimated by the following formula;

$$R_{\text{Air}} = \frac{{\rho_{\text{Air}} }}{2} \cdot C_{\text{A}} \cdot A_{\text{X}} \cdot V_{\text{W}}^{2}$$

(4.7)

New value of K _T/J ² (K _T,NW/J ²_NW ) is obtained as follows;

$$\begin{aligned} \frac{{K_{\text{T,NW}} }}{{J_{\text{NW}}^{2} }} & = \frac{{R - R_{\text{Added}} + R_{\text{Air}} }}{{\rho_{\text{SW}} \cdot (1 - t) \cdot V_{\text{A}}^{2} \cdot D_{\text{P}}^{2} }} \\ & = \frac{{K_{\text{T,NA}} }}{{J_{\text{NA}}^{2} }} + \frac{{R_{\text{Air}} }}{{\rho_{\text{SW}} \cdot (1 - t) \cdot V_{\text{A}}^{2} \cdot D_{\text{P}}^{2} }} \\ \end{aligned}$$

(4.8)

The new values of J (J _NW) and K _Q (K _Q,NW) are evaluated by use of propeller open-water characteristics, J _NW from K _T,NW/J ²_NW at first and then K _Q,NW from J _NW.

During the correction, V _W and therefore V _A is kept unchanged, and the new value of N _P (N _P,NW) is obtained by the following formula.

$$N_{\text{P,NW}} = N_{\text{P,NA}} \cdot \frac{{J_{\text{NA}} }}{{J_{\text{NW}} }}$$

(4.9)

The new values of P _D (P _{D ,NW}) and then P _B (P _{B ,NW}) are calculated by the following formulae.

$${{P}_{\text{D}}}_{\text{,NW}} = \frac{{2\pi \cdot \rho_{\text{SW}} \cdot (N_{\text{P,NW}} /60)^{3} \cdot K_{\text{Q,NW}} \cdot D_{\text{P}}^{5} }}{{\eta_{\text{R}} }}$$

(4.10)

$$\begin{aligned} {{P}_{\text{S}}}_{\text{,NW}} & = \frac{{{{P}_{\text{D}}}_{\text{,NW}} \times {\text{no}} .\;{\text{of}}\;{\text{propellers}}}}{{\eta_{\text{S}} }} \\ {{P}_{\text{B}}}_{\text{,NW}} & = {{P}_{\text{S}}}_{\text{,NW}} /\eta_{\text{G}} \\ \end{aligned}$$

(4.11)

The values of P _{B ,NW}, N _P,NW together with V _W comprise the final analysed results of the speed trial.

5 New procedure for tidal current correction

The author wants to propose the procedure for tidal current correction presented in Sect. 5.3. The background investigations are explained in detail in Sects. 5.1 and 5.2.

5.1 Expression of V _C

5.1.1 Characteristics of tidal current

It is said “Tidal changes are the net result of multiple influences that act over varying periods. These influences are called tidal constituents. The primary constituents are the Earth’s rotation, the positions of the Moon and the Sun relative to Earth, the Moon’s altitude above the Earth’s equator, and underwater topography.” As the result, tidal elevation and tidal current velocity are expressed by the summation of a number of harmonic functions.

In the homepage of the Geodetic Society of Japan [11], a table is given where the characteristic values of 24 tidal constituents are listed. They are name of constituent, origin, tidal amplitude and period. From them, a scale of velocity amplitude is calculated by amplitude/period. Table 2 shows seven principal tidal constituents with bigger values of the scale of velocity amplitude.

Table 2 Principal tidal constituents estimated for the earth approximated by a rigid ellipsoid

It is said that practical estimation of tide and tidal current velocity can be made by using six to ten tidal constituents, although the Tide Tables prepared by the Japan Coast Guard are estimated by the superposition of some sixty tidal constituents. Tidal current velocity estimated by summation of N tidal constituents is written as follows:

$$V_{\text{C}} = V_{\text{C,0}} + \sum\limits_{i = 1}^{N} {\left\{ {V_{{{\text{C,C}},i}} \cdot \cos \left( {\frac{2\pi }{{\text{T}_{{{\text{C}},i}} }} \cdot t} \right) + V_{{{\text{C,S}},i}} \cdot \sin \left( {\frac{2\pi }{{\text{T}_{{{\text{C}},i}} }} \cdot t} \right)} \right\}}$$

(5.1)

5.1.2 Examples of the variations of tidal current velocity

Japan Coast Guard publishes, on the website [12], the forecast of tidal current velocity at the major channels in Japan. From the website, the values of tidal current velocity at the channel named “Hayasui-no-seto” from January 1st to 18th, 2013 are obtained. The obtained values are shown by the circles in Fig. 10.

Fig. 10

Current velocity variation at “Hayasui-no-Seto”

“Hayasui-no-Seto” is one of the four channels through which Seto Inland Sea is connected to the outer seas, and the current velocity there is very closely correlated to that at a principal speed trial site in Japan [13]. The location of “Hayasui-no-Seto” is shown by an arrow in Fig. 11.

Fig. 11

Location of “Hayasui-no-Seto” (33°18′N, 131°58′E)

Hydrographic and Oceanographic Department of Japan Coast Guard publishes two volumes of “Tide Tables” every year. In the second volume [14], there is information on the variations of tidal current at five ship passages in the outskirts of the Pacific Ocean. The names of locations are listed below and locations are shown by arrows in Figs. 12, 13, and 14.

Fig. 12

Locations of “Off One Fathom Bank”, “Phillip Channel” and “Batu Berhanti” (from the left)

Fig. 13

Location of “Juan de Fuca Strait Entrance”

Fig. 14

Location of “San Francisco Bay Entrance”

• a) Off One Fathom Bank, Malacca Strait (2°40′N, 101°10′E)

• b) Phillip Channel, Off Singapore (1°06′N, 103°44′E)

• c) Batu Berhanti, Off Singapore (1°12′N, 103°53′E)

• d) Juan de Fuca Strait Entrance (48°27′N, 124°35′W)

• e) San Francisco Bay Entrance (37°49′N, 122°30′W)

The listed information is the forecasts of the extreme values of current velocity paired with the corresponding time, and the time of zero cross of current velocity every day. The listed data in the volume from January 1st to 18th, 2013 are shown by the circles in Figs. 15, 16, 17, 18, 19.

Fig. 15

Current velocity variation at “Off One Fathom Bank”

Fig. 16

Current velocity variation at “Phillip Channel”

Fig. 17

Current velocity variation at “Batu Berhanti”

Fig. 18

Current velocity variation at “Juan de Fuca Strait Entrance”

Fig. 19

Current velocity variation at “San Francisco Bay Entrance”

5.1.3 Analysis and the results

To characterize the patterns of tidal current variation, the above data are fitted by the linear combination of the seven tidal constituents shown in Table 2 and a constant term.

To obtain the reasonable fitted results, it would be necessary to analyse long enough data. To decide how long data should be analysed, the variation of tidal current velocity at “Hayasui-no-Seto” from January 1st to February 9th is analysed while the data length is changed from 7 to 40 days. Obtained amplitudes of tidal constituents are shown in Figs. 20 and 21, being plotted over the length of analysed data. The obtained amplitudes of constituents seem to converge at the data length over 30 days. Then, the author concludes the analysis of the data of 35 days would give reasonable results.

Fig. 20

Amplitudes of tidal constituents with about a half day period vs. analysed data length

Fig. 21

Amplitudes of tidal constituents with about 1 day period vs. analysed data length

The data shown by circles in Figs. 15, 16, 17, 18 and 19 are collected for 35 days from January 1st, 2013, and they, together with the data at “Hayasui-no-Seto”, are fitted by the linear combination of the seven tidal constituents and a constant term. The fitted results are shown by the solid lines in the Figs. 10 and from Figs. 15, 16, 17, 18 and 19. Values of normalised standard deviation of the fitting error E defined by the following formula are less than 5 %.

$$E = \frac{2}{{{\text{Max}}(d_{i} ) - {\text{Min}}(d_{i} )}} \cdot \sqrt {\frac{1}{N} \cdot \sum\limits_{i = 1}^{N} {(d_{i} - f_{i} )^{2} } }$$

(5.2)

where, d _i , f _i , N: values of given data, fitted results and total number of given data, Max(d _i ), Min(d _i ): maximum and minimum values of d _i.

The amplitudes of seven constituents obtained by the analysis are presented in Table 3, being normalised by the maximum amplitude among them. In Table 3, the constituents with maximum amplitude are shown in bold. The values shown in Table 3 are plotted over the name of constituents in Fig. 22.

Table 3 Amplitudes of constituents normalised by the maximum amplitude

Fig. 22

Normalised amplitudes of tidal constituents obtained by the analyses of current variations for 35 days

The variations of current velocity at the four places except “Phillip Channel” and “Batu Berhanti”, shown in Figs. 10, 15, 18 and 19, look quite similar, and have the characteristics that current velocity varies like a harmonic function with the period of around a half day while the peak or trough value of individual wave changes one by one. In contrast, the variations of current velocity at “Phillip Channel” and “Batu Berhanti”, presented in Figs. 16 and 17, show the domination by the variations with the period of around 1 day. Table 3 and Fig. 22 also support the facts, where clear dominations of M ₂ constituent having a period around a half day are observed at the four places, while K ₁ and O ₁ constituents having periods around 1 day are dominant at “Phillip Channel” and “Batu Berhanti”.

From the figures showing the locations of the six places, it is clear that the topography around “Phillip Channel” and “Batu Berhanti” are quite complicated in comparison with the other four places. It would be the main reason of the difference; complicated topography around may prevent the shorter period tides to be developed, and longer period tides may prevail in such places.

5.1.4 Expression for the variation of tidal current velocity

From the above investigation, the author considers that we can find without much difficulty a site of speed trial where the tidal constituents with around a half day period are dominant. Then, the author tries to find an expression for the variation of tidal current velocity, on the assumption that speed trials are carried out at such places.

From the current velocity variation at “Hayasui-no-Seto” shown in Fig. 10, a two-day-part from 10th day to 11th day containing relatively large difference of peak and trough values is selected. The result is shown in Fig. 23, which is the calculated variation of current velocity by the fitted results of seven tidal constituents. This variation is used for the investigation.

Fig. 23

An example of tidal current variation over 2 days

The values of current velocity in Fig. 23 seem too big for those at speed trial sites. However, it can be used for the investigation because only the variation pattern is important.

Let us suppose that speed trials of double runs for four engine outputs are performed in the current velocity variation shown in Fig. 23, and the first trial run is measured at 5:00 on the 10th day. The first example is the case where the interval between the trial runs is 1.5 h. In this case, the duration of speed trial is less than a half day, and the variation of current velocity at the trial runs can be fitted well by the formula (2.3), i.e. summation of M ₂ constituent and a constant term.

In Fig. 24, △ marks show the fitted results by the formula (2.3), and the assumed current velocity variation extracted from Fig. 23 is shown by a solid line. In the case, variation of current velocity contains up to two extreme values, and we do not need to consider the characteristics that peak or trough value of individual wave changes one by one. As the results, fitting by the formula 2.3 works very well as observed in Fig. 24. The value of E is 2.1 % in the case.

Fig. 24

Tidal current velocity variation and fitted results (1)

However, when the duration of speed trial becomes longer than a half day, we have to consider the possibility that variation of current velocity contains three extreme values. The second example is the case where the starting time of the trial is the same and the interval between the runs is increased to 2 h.

Comparison between the assumed current velocity and the fitted results by the formula (2.3), shown by the marks △, is presented in Fig. 25. Because the values of current velocity at 7:00 and 19:00 on the 10th day are significantly different, the fitted values by the formula (2.3) are somewhat far from the assumed current velocity variation shown by the solid line, especially at places close to the two peaks. The value of E increases to 8.2 % in the case.

Fig. 25

Tidal current velocity variation and fitted results (2)

In this case, amplitudes of three consecutive half waves are different, and we have to include the second constituent which has the period of an exact half day in the expression of current velocity, as shown in the following formula.

$$\begin{aligned} V_{\text{C}} & = V_{\text{C,0}} + V_{\text{C,C}} \cdot \cos \left( {\frac{2\pi }{{\text{T}_{\text{Tide}} }} \cdot t} \right) + V_{\text{C,S}} \cdot \sin \left( {\frac{2\pi }{{\text{T}_{\text{Tide}} }} \cdot t} \right) \\ & \quad + V_{\text{C,C}}^{'} \cdot \cos \left( {\frac{2\pi }{{0.5\;{\text{day}}}} \cdot t} \right) + V_{\text{C,S}}^{'} \cdot \sin \left( {\frac{2\pi }{{0.5\;{\text{day}}}} \cdot t} \right) \\ \end{aligned}$$

(5.3)

The fitted results by the formula (5.3) are shown by ○ marks in Fig. 25. Fitting accuracy is improved, and the value of E decreases to 1.5 %.

However, the use of the formula (5.3) increases the number of unknown coefficients to 5 from 3 of the formula (2.3), which had better be kept as small as possible. An expedient to reduce the number of unknown coefficients is the formula (5.4);

$$\begin{aligned} V_{\text{C}} & = V_{\text{C,0}} + V_{\text{C,1}} \cdot t \\ & \quad + V_{\text{C,C}} \cdot \cos \left( {\frac{2\pi }{{\text{T}_{\text{Tide}} }} \cdot t} \right) + V_{\text{C,S}} \cdot \sin \left( {\frac{2\pi }{{\text{T}_{\text{Tide}} }} \cdot t} \right) \\ \end{aligned}$$

(5.4)

This formula works well as shown by the marks × in Fig. 25. The value of E is 1.8 % in the case.

The formula (5.4) cannot be applied if the duration of speed trial becomes longer than a day, where we have to expect the possibility of variation of current velocity having four or more extreme values. In such case, the application of the formula (5.3) should be tried. However, even in the cases of VLCC trials for which the longest time of approach run is necessary at present, the total duration time of the speed trial with 8 runs is much less than 1 day. Therefore, the formula (5.4) works well in most cases.

As a conclusion, the author adopts the formula (5.4) as the expression of the variation of V _C. However, the formula (2.3) can also be used for the analysis of speed trials the duration of which is shorter than a half day.

5.2 Expression of V _W

5.2.1 Candidate formulae

At first, three candidate formulae were raised for the expression of V _W in no air condition. It was expected the best one could be selected through the analysis of simulated speed trial results and the comparison of the analysed results with the assumed values.

5.2.1.1 K _Q in propeller open-water characteristics

K _Q in propeller open-water characteristics is well expressed by a function of J, and we can rewrite K _Q and J as;

$$\begin{aligned} K_{\text{Q}} & = \frac{Q}{{\rho \cdot n_{\text{P}}^{2} \cdot D_{\text{P}}^{5} }} = \frac{{{P_{\text{B}}} \cdot \eta_{\text{B}} \cdot \eta_{\text{S}} \cdot \eta_{\text{R}} }}{{2\pi \cdot \rho_{\text{SW}} \cdot n_{\text{P}}^{3} \cdot D_{\text{P}}^{5} }}, \\ J & = \frac{{V_{\text{A}} }}{{n_{\text{P}} \cdot D_{\text{P}} }} = \frac{{V_{\text{W}} \cdot (1 - w_{\text{S}} )}}{{n_{\text{P}} \cdot D_{\text{P}} }} \Rightarrow V_{\text{W}} = \frac{{J \cdot n_{\text{P}} \cdot D_{\text{P}} }}{{1 - w_{\text{S}} }} \\ \end{aligned}$$

(5.5)

Because η _B and η _S are considered almost constant, and η _R and w _s do not change much with the change of ship speed, we can get the following rough proportionalities.

$${{P}_{\text{B}}} \propto K_{\text{Q}} \cdot N_{\text{P}}^{3} ,\quad V_{\text{W}} \propto J \cdot N_{\text{P}}$$

(5.6)

where, ∝ does not mean “precisely proportional to”, but only “roughly”. Then, if we write K _Q by a first order function of J, we can obtain

$$K_{\text{Q}} = a \cdot J + b \Rightarrow {{P}_{\text{B}}}/N_{\text{P}}^{3} = A_{1} \cdot V_{\text{W}} /N_{\text{P}} + A_{2}$$

(5.7)

$$\begin{aligned} V_{\text{W}} & = {{P}_{\text{B}}}/(A_{1} \cdot N_{\text{P}}^{2} ) - A_{2} \cdot N_{\text{P}} /A_{1} \\ & = B_{1} \cdot {{P}_{\text{B}}}/N_{\text{P}}^{2} + B_{2} \cdot N_{\text{P}} \\ \end{aligned}$$

(5.8)

where, a, b, A ₁, A ₂, B ₁, B ₂ are appropriate coefficients.

However, in some cases, it is found that constant term should be added as shown in the following formula, to obtain better fitting of speed and power relations.

$$V_{\text{W}} = B_{1} \cdot {{P}_{\text{B}}}/N_{\text{P}}^{2} + B_{2} \cdot N_{\text{P}} + B_{3}$$

(5.9)

5.2.1.2 Function of power only (polynomial function)

Because it is so common to show the results of power estimation by a plot of P _B vs. V _W, it is worth trying an expression of V _W as a function of power only. The selected expression is a simple fourth order polynomial function as follows;

$$\begin{aligned} V_{\text{W}} = A_{0} + A_{1} \cdot {{P}_{\text{B}}} + A_{2} \cdot {{P}_{\text{B}}}^{2} + A_{3} \cdot {{P}_{\text{B}}}^{3} + A_{4} \cdot {{P}_{\text{B}}}^{4} \\ \end{aligned}$$

(5.10)

5.2.1.3 Another function of power only

In the time being, the 27th ITTC specialist committee on “Performance of Ships in Service” proposed the following formula to relate V _W with P _B;

$$V_{\text{W}} = a + b \cdot {{P}_{\text{B}}}^{\text{P}}$$

(5.11)

To obtain the unknowns: a, b and P, the committee proposed the use of a new tool like Solver Macro of Microsoft Excel [15]. Although the solving process is not clear enough, it is worth checking because the results can be obtained anyhow.

5.2.2 Evaluations

Used in conjunction with the formula (5.4), formulae (5.8) and (5.9) work well when they are applied to simulated trial results. However, when specialists in Japanese shipyards applied them to the actual examples of trial results, they found that those formulae sometimes give strange results. The suspected reason is as follows: because the formula (5.8) and (5.9) uses two measured items namely P _B and N _P, and because the measured data inevitably contain some scatter, the estimated V _W may deviate into unexpected direction.

To avoid such instability in solving process, the use of V _W formula with single measured item such as formulae (5.10) and (5.11) may be better. Then, the shipyard specialists analysed their own trial results using formulae (5.10) and (5.11), and found that stability of the analysed results is greatly improved when the formula (5.11) is used.

However, it is considered that more robust procedure should be pursued, because actual measured data may have unexpected scatter. In such cases, instability of the analysed results might be observed again even when the formula (5.11) is used.

5.2.3 A counter measure

What occurs in the cases referred to as “instability of the analysed results” is, in most cases, the shape of speed and power relation curve becomes strange. As commonly understood, required power is roughly proportional to the third power of ship speed. However, in such cases of instability, the curve becomes far from such shape. It seems to be caused by the too much freedom in the both formulae of speed-power relation and current velocity variation.

Then, it would be better to use the formula of speed and power relation with the least degree of freedom while keeping the usual shape on the speed-power plane. One solution may be the following formula;

$$V_{\text{W}} = V_{\text{W,NA}} ({{P}_{\text{B}}}) + \Delta V_{\text{W}}$$

(5.12)

where V _W,NA(P _B) is a fitted function of the speed and power relation in no air condition estimated anyhow (usually from tank test results).

5.3 Analysis procedure

When the proposed analysis procedure is employed, it is required to carry out several up and down runs, not necessarily composed of double runs with the same engine outputs. However, it is supposed here, like the present practice, that pairs of up and down trial runs for n engine outputs (2 × n trial runs in total) are performed. Then, 2 × n combinations of measured averages of V _G, P _B and N _P are obtained, and P _B and N _P are corrected to no air condition while V _G is not changed at all. As the results,

$$[V_{{{\text{G}},i}} ,{{P}_{\text{B}}}_{{{\text{,NA}},i}} , \, N_{{{\text{P}},{\text{NA}},i}} ] \, (i = 1, 2, 3\ldots 2n)$$

are obtained.

5.3.1 Different natures of two formulae

Now, the formulae (5.4) and (5.12) are used, and plugging them into the formula (4.6), we obtain linear simultaneous equations of unknown coefficients. However, we have to consider the fact that the natures of the two formulae are different.

From the investigation explained in Sect. 5.1, it can be expected that the fitted results by the formula (5.4) would be a reasonable estimation of what happened during the trial runs. In contrast, in the case of formula (5.12), V _W,NA(P _B) is just an estimation and, even if the best-fit value of ΔV _W is obtained by the analysis, general tendency of the actual speed and power relation cannot be necessarily fitted well by the formula (5.12).

Then, it would be better to deal with the two formulae separately by applying iteration process of BSRA standard method [10] than to solve simultaneous equations directly.

5.3.2 Iteration process by BSRA standard method

When BSRA standard method is employed, the equations for V _W are solved at first, by putting the values of measured V _G in the place of V _W, as shown in the following formula,

$$\left[ {\begin{array}{*{20}c} {V_{\text{G,1}} - V_{\text{W,NA}} ({{P}_{\text{B}}}_{\text{,NA,1}} )} \\ {V_{\text{G,2}} - V_{\text{W,NA}} ({{P}_{\text{B}}}_{\text{,NA,2}} )} \\ \vdots \\ {V_{{{\text{G}},2n}} - V_{\text{W,NA}} ({{P}_{\text{B}}}_{{{\text{,NA,2}}n}} )} \\ \end{array} } \right] = [\Delta V_{\text{W}} ] \cdot \left[ {\begin{array}{*{20}c} 1 \\ 1 \\ \vdots \\ 1 \\ \end{array} } \right]$$

(5.13)

and the least square solution of ΔV _W is obtained by the simple average of V _G,i  − V _W,NA(P _{B ,NA,i} ). Then, the fitted values of V _W,i which is written as V _WF,i are calculated as follows;

$$V_{\text{WF,i}} = V_{\text{W,NA}} ({{P}_{\text{B}}}_{{{\text{,NA}},i}} ) + \Delta V_{\text{W}}$$

(5.14)

The V _WF,i are plugged into the formula (4.6) and the values of V _C,i which is written as V _CO,i are obtained as follows;

$$V_{{{\text{CO}},i}} = \pm (V_{{{\text{G}},i}} - V_{{{\text{WF}},i}} )$$

(5.15)

where, double sign (±) reflects the ship’s heading.

Then, the following equations are applied to the obtained V _CO,i to fit the variation of V _C by the formula (5.4), and the fitted values of V _C,i written as V _CF,i , are calculated by use of the obtained coefficients as shown in the equation (5.17).

$$\left[ {\begin{array}{*{20}c} {V_{{{\text{CO,}}1}} } \\ {V_{\text{CO,2}} } \\ \vdots \\ {V_{{{\text{CO,2}}n}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {C({t}_{1} )} & {S({t}_{1} )} & {{t}_{1} } & 1 \\ { - C({t}_{2} )} & { - S({t}_{2} )} & { - {t}_{2} } & { - 1} \\ \vdots & \vdots & \vdots & \vdots \\ { - C({t}_{2n} )} & { - S({t}_{2n} )} & { - {t}_{2n} } & { - 1} \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {V_{\text{C,C}} } \\ {V_{\text{C,S}} } \\ {V_{\text{C,1}} } \\ {V_{\text{C,0}} } \\ \end{array} } \right]$$

(5.16)

$$V_{{{\text{CF}},i}} = \pm \{ V_{\text{C,C}} \cdot C({t}_{i} ) + V_{\text{C,S}} \cdot S({t}_{i} ) + V_{\text{C,1}} \cdot {t}_{i} + V_{\text{C,0}} \}$$

(5.17)

In these equations, the following abbreviations are used.

$$C(t) \, = {\text{ cos(2}}\pi \cdot t/\text{T}_{\text{Tide}} ),\,S (t ) { } = {\text{ sin(2}}\pi \cdot t/\text{T}_{\text{Tide}} )$$

(5.18)

The fitted V _CF,i are plugged into the formula (4.6) and the new values of V _W,i which is written as V _WO,i are obtained as follows;

$$V_{{{\text{WO,}}i}} = V_{{{\text{G}},i}} \mp V_{{{\text{CF}},i}}$$

(5.19)

Next, V _G,i in the left hand side of the equation (5.13) are replaced by the obtained V _WO,i as follows;

$$\left[ {\begin{array}{*{20}c} {V_{\text{WO,1}} - V_{\text{W,NA}} ({{P}_{\text{B}}}_{\text{,NA,1}} )} \\ {V_{\text{WO,2}} - V_{\text{W,NA}} ({{P}_{\text{B}}}_{\text{,NA,2}} )} \\ \vdots \\ {V_{{{\text{WO,}}2n}} - V_{\text{W,NA}} ({{P}_{\text{B}}}_{{{\text{,NA,2}}n}} )} \\ \end{array} } \right] = [\Delta V_{\text{W}} ] \cdot \left[ {\begin{array}{*{20}c} 1 \\ 1 \\ \vdots \\ 1 \\ \end{array} } \right]$$

(5.20)

The equations are solved in the same way to obtain the new values of ΔV _W, and the revised values of V _WF,i are calculated by the formula (5.14). This iteration process should be repeated until the values of V _W,i and V _C,i become stable.

At each iteration stage, two sets of V _W,i and V _C,i are obtained as explained above. One set is the fitted one calculated from each formula with fitting coefficients; they are called “fitted V _W or V _C” and written as V _WF,i or V _CF,i in this paper. The other is obtained from formula (4.6) and the fitted values of V _W or V _C; they are called “obtained V _W or V _C” and written as V _WO,i or V _CO,i . Among them, V _CF,i and V _WO,i are considered closer to the actual values, when the difference of the natures of the two formulae (5.4) and (5.12) is reflected.

After the iteration process is over, the differences of V _WO,i and V _WF,i are calculated and fitted by (n − 1)th order polynomial function of P _{B ,NA,i} . Polynomial function of (n − 1)th order is used, because trial measurements are performed for n pair of engine outputs. Then, the fitted results are applied to correct the values of V _WF,i , and the final results of V _W,i are obtained.

5.3.3 Analysed example of a simulated speed trial results

The simulated speed trial results shown in Fig. 8 (the original simulation with approach length of 16 sea miles) are analysed by the iteration process.

Because V _W,NA(P _B) of the ship under trial is unknown at the stage of speed trial analysis, V _W,NA(P _B) used for the analysis must be somewhat different from the characteristics used for the trial simulation. In the following example, V _W,NA(P _B) used for the speed trial analysis is obtained by fitting the data shown by △ marks in Fig. 26, which is slightly different from the assumed characteristics used to obtain the simulated speed trial results shown by the solid line.

Fig. 26

Comparison of speed-power relations assumed for speed trial simulation and used for the analysis

The results obtained after the 4th iteration are shown in Fig. 27. The results of V _WF,i shown by × marks do not agree well to the assumed solid line, because V _W,NA(P _B) used for the analysis has different slope from the one of the ship under trial.

Fig. 27

Plots on V _G, V _W − P _B plane of simulated trial results analysed by the iteration process

Differences between V _WF,i and V _WO,i defined as follows

$$\Delta V_{{{\text{W,O}} - {\text{F}}}} = V_{{{\text{WO}},i}} - V_{{{\text{WF}},i}}$$

(5.21)

are plotted over P _B by ◇ marks in Fig. 28, and fitted by third order polynomial function as shown by the solid line. The values on the line are used to correct V _WF,i obtained by the iteration, and the final values of V _W are obtained as shown by * marks in Fig. 27, which agree well to the assumed curve.

Fig. 28

Differences between fitted and obtained V _W

As the results of the analysis, ship speed through the water V _W is obtained by the following function in this case;

$$\begin{aligned} V_{\text{W}} & = V_{\text{W,NA}} ({{P}_{\text{B}}}) + \Delta V_{\text{W}} + \Delta V_{{{\text{W,O}} - {\text{F}}}} \\ & = V_{\text{W,NA}} ({{P}_{\text{B}}}) + \Delta V_{\text{W}} \\ & \quad + a_{1} + a_{2} \cdot {{P}_{\text{B}}} + a_{3} \cdot {{P}_{\text{B}}}^{2} + a_{4} \cdot {{P}_{\text{B}}}^{3} \\ \end{aligned}$$

(5.22)

where from a ₁ to a ₄ are fitting coefficients. In this way, stable solution with well-fitted results is acquired finally.

The results of current velocity variation of the same analysis are shown in Fig. 29. The fitted values of V _C (V _CF,i ) by the formula (5.4) are shown by ◇ marks, which agree well to the assumed curve. However, the obtained values of V _C (V _CO,i ) shown by □ marks do not agree well to the assumed curve because of the difference between two V _W,NA(P _B)s, assumed for the analysis and used for the trial simulation.

Fig. 29

Variation of tidal current velocity obtained by the iteration process

Standard deviations of V _WO,i  − V _W,Assumed, V _CO,i  − V _CF,i , V _CF,i  − V _C,Assumed at each iteration stage are shown in Fig. 30. Obtained tendencies from the third iteration to the fourth iteration seem to be very stable, and the both differences of V _WO and V _CF from the assumed values shown by × and ◇ marks become very small.

Fig. 30

Standard deviations of differences of the obtained results at each iteration stage

However, as shown by □ marks in Fig. 30, difference between V _CO,i and V _CF,i does not become as small as the above, reflecting the difference between the values of two V _W,NA(P _B)s.

As explained in the above, the analysed results of simulated trial results by the method proposed in this paper agree very well to the values assumed for the speed trial simulation. Thus, the effectiveness of the proposed analysis procedure is confirmed.

6 Conclusions

In this paper, the author intended to revise the analysis procedure of speed trial results, mainly a part of the correction of tidal current effect. After he identified the correction is extremely difficult in the cases of low speed full ships, he made his proposal and checked the applicability by use of simulated speed trial results of a VLCC. As the conclusions of the study, the author summarises the results as follows;

• (1) The measured values of power and propeller revolution should be corrected to the ones corresponding to no air condition. For the correction, the application of method by use of propeller open-water characteristics is recommended.

• (2) The values of tidal current velocity at the time of the trial runs should be estimated by use of the corrected results to no air condition. After the estimation, the values of ship speed through the water are estimated. Then, the values of power and propeller revolution should be corrected to the ones corresponding to no wind condition. The method used for (1) can be applied for the correction, too.

• (3) To up-date the correction procedure for tidal current effect, appropriate functions for ship speed through the water and tidal current velocity are investigated. Tidal current velocity can usually be understood to vary with the dominant effect of the so-called M ₂ tidal constituent.

• (4) By use of the functions, linear simultaneous equations can be formulated, and by the solution of them the values of ship speed through the water and current velocity can be estimated. However, in this paper, solution by iteration process is more intensely investigated.

• (5) In the cases where current velocity variation can be expressed by the so-called M ₂ tidal constituent, the analysed results of simulated speed trial results agree well to the assumed values.

• (6) The correction procedure of current effect for the results of speed trial of low speed full ships needs rather complicated process. The author believes the process is necessary even under the present situation, unless a reliable equipment to measure ship speed through the water is available onboard.

• (7) The applicability of the proposed procedure should be confirmed further by the analyses of actual speed trial data, because it is confirmed only by use of the results of simulated speed trial in this paper.

Appendix: Corrections to no air condition

During the analysis, Schoenherr’s, Taniguchi–Tamura’s and BSRA standard methods correct the measured results to the corresponding ones in no air condition. Why do we have to correct to no air condition and correct again to no wind condition after the correction of tidal current effect? Why can’t we just correct to no wind condition directly? It is worth discussing the reason here.

We suppose there is only current, and the ship sails on the same course against and to the current in no air condition. If we further suppose the engine outputs during up and down runs are controlled to the same level, the ship speed through the water would be kept the same. In this case, ship velocities over the ground are different only because of current. Then, current velocity can be estimated by half of the difference of the measured ship velocity over the ground, if we can neglect the change of current velocity.

However, if it is in no wind condition, there is air around the ship. Because ship velocity relative to air is the same as the one over the ground, the values are different as illustrated in Fig. 31. Then, the values of air resistance are different between up and down runs, and the parts of engine outputs shared to overcome the air resistance are different.

Fig. 31

A ship sailing in no wind condition

Even if we control engine outputs to the same level during up and down runs in this condition, the values of ship velocity through the water are different because the parts of engine outputs shared to overcome the resistance from water are different. Then, the difference can cause error in the estimation of tidal current velocity.

Precisely speaking, the above explanation is right. However, it seems to the author the effect is almost negligible for many cases. The above mentioned difference of air resistance can be written as follows;

$$\begin{aligned} \Delta R_{\text{Air}} & = \frac{{\rho_{\text{Air}} }}{2} \cdot C_{\text{A}} \cdot A_{\text{X}} \cdot \left\{ {(V_{\text{W}} + V_{\text{C}} )^{2} - (V_{\text{W}} - V_{\text{C}} )^{2} } \right\} \\ & = \frac{{\rho_{\text{Air}} }}{2} \cdot C_{\text{A}} \cdot A_{\text{X}} \cdot 4 \cdot V_{\text{W}} \cdot V_{\text{C}} \\ \frac{{\Delta R_{\text{Air}} }}{{R_{\text{Air}} }} & = \frac{{4 \cdot V_{\text{W}} \cdot V_{\text{C}} }}{{V_{\text{W}}^{2} }} = 4 \cdot \frac{{V_{\text{C}} }}{{V_{\text{W}} }} \\ \end{aligned}$$

(7.1)

The ratio of V _C to V _W is usually less than 10 %. Then, ΔR _Air/R _Air is less than 40 %. As the so-called air allowance (ratio of air resistance to water resistance) is up to 5 % for usual ships, the ratio of the difference in air resistance (ΔR _Air) to the ship resistance is up to 2 %. Although whether 2 % can be negligible or not should be discussed, there is considerable possibility that the correction to no air condition can be skipped for the majority of cases. However, in some cases where the ratio of current velocity to ship speed is relatively large, and/or air resistance in no wind condition is relatively large due to a very big superstructure for examples, it cannot be skipped.

It would be a matter of serious consideration in the days of manual calculation. However, because calculation tools are quite powerful nowadays, the author thinks that we had better correct the measured data by way of no air condition in all cases. It is only a matter of programming or preparation of a worksheet and the calculation itself would be completed almost in an instant.