Application of consistency checking to evaluation of uncertainty in multiple replicate measurements

Abstract

Use of repeated measurements in quantitative chemical analysis is common but leads to the problem of how to combine the measurement values and produce a result with an uncertainty following the GUM. There is often confusion between repeated indications or observations of an input quantity, for whose uncertainty the GUM prescribes a type A evaluation, and complete measurements repeated on multiple sub-samples, as considered here. A solution for combining repeated measurement results and their individual uncertainties based on simple interval logic is proposed here. The individual measurement values and their uncertainties are compared with the calculated average value to see if this implies that another, possibly unknown, source of uncertainty is present. The model of the individual results is modified for this possible between-replicate effect so that the repeated measurements are consistent. Lack of consistency is a strong indication that the measurement is not fully under control and needs further development or investigation. This is not always possible, however and the method given here is proposed to ensure that the values of the repeated measurements agree with each other. A simple numerical example is given showing how the method can be implemented in practice.

Appendices

Appendix 1: The symbols used in this paper

Y _i :

Value of the measurands; variable representing the state of knowledge

u(y _i ):

Standard uncertainty associated with result Y _i

X _i :

Input quantity; variable representing the state of knowledge

u(x _i):

Standard uncertainty associated with the input quantity X _i

r(x _i , x _j ):

Correlation coefficient between X _i and X _j

c _i :

Concentration for replicate i (results of the measurements)

c _x :

Average concentration (end result)

ε _i :

Difference between single result c _i and the average c _x

I _i :

Observed intensity (detector output) for replicate i

δc _i :

Small deviation of the concentration with expectation zero

Appendix 2: Calculation of the minimum additional uncertainty for the equivalence check

In cases when a non-weighted arithmetic mean is used to combine measurement results, a general equation for the minimum additional uncertainty u(δ _i) that should be added to the n replicates can be derived. One contribution Y _m can be separated from the arithmetic mean.

$$ \overline Y = \frac{1} {n}\sum\limits_{i = 1}^n {Y_i } = \frac{{Y_m }} {n} + \frac{1} {n}\sum\limits_{i \ne m}^{} {Y_i } $$

(13)

The difference between the average and Y _m is:

$$ \varepsilon _m = Y_m - \overline Y $$

(14)

Combining Eqs. (13) and (14) gives:

$$ \varepsilon _m = Y_m - \left[ {\frac{{Y_m }} {n} + \frac{1} {n}\sum\limits_{i \ne m}^{} {Y_i } } \right] = \frac{{n - 1}} {n} \cdot Y_m - \frac{1} {n}\sum\limits_{i \ne m}^{} {Y_i } $$

(15)

An independent uncertainty component is added to all replicates, which leads to a second difference ε ^* _m :

$$\varepsilon ^{*}_{m} = \frac{{n - 1}}{n} \cdot {\left( {Y_{m} + \delta _{m} } \right)} - \frac{1}{n}{\sum\limits_{i \ne m}^{} {{\left( {Y_{i} + \delta _{i} } \right)} = {\left[ {\frac{{n - 1}}{n} \cdot Y_{m} - \frac{1}{n}{\sum\limits_{i \ne m}^{} {Y_{i} } }} \right]} + {\left[ {\frac{{n - 1}}{n} \cdot \delta _{m} - \frac{1}{n}{\sum\limits_{i \ne m}^{} {\delta _{i} } }} \right]}} } $$

(16)

The two terms in Eq. (16) are obviously independent and the left term is equal to difference without the additional terms. The uncertainty of ε ^* _m can be calculated.

$$ u^2 (\varepsilon _m^* ) = u^2 (\varepsilon _m^{} ) + u^2 \left( {\frac{{n - 1}} {n} \cdot \delta _m - \frac{1} {n}\sum\limits_{i \ne m}^{} {\delta _i } } \right) $$

(17)

$$ u^2 \left( {\frac{{n - 1}} {n} \cdot \delta _m - \frac{1} {n}\sum\limits_{i \ne m}^{} {\delta _i } } \right) = \left( {\frac{{n - 1}} {n}} \right)^2 \cdot \, u^2 (\delta _m ) + \frac{1} {{n^2 }}\sum\limits_{i \ne m}^{} {u^2 (\delta _i )} $$

(18)

All uncertainties of the additional terms have the same value u(δ).

$$u^{2} {\left( {\frac{{n - 1}}{n}\delta _{m} - \frac{1}{n}{\sum\limits_{i \ne m}^{} {\delta _{i} } }} \right)} = {\left( {\frac{{n - 1}}{n}} \right)}^{2} u^{2} (\delta ) + {\left( {\frac{{n - 1}}{{n^{2} }}} \right)}u^{2} (\delta ) = \frac{{(n - 1)^{2} + n - 1}}{{n^{2} }}u^{2} (\delta ) = \frac{{n - 1}}{n}u^{2} (\delta ) $$

(19)

Combining Eqs. (17) and (19) leads to:

$$ u^2 (\varepsilon _m^* ) = u^2 (\varepsilon _m^{} ) + \frac{{n - 1}} {n} \cdot u^2 (\delta ) $$

(20)

Equation (20) solved for u(δ):

$$ \begin{gathered} u^2 (\delta ) = \frac{n} {{n - 1}} \cdot \left[ {u^2 (\varepsilon _m^* ) - u^2 (\varepsilon _m^{} )} \right] \hfill \\ u(\delta ) = \sqrt {\frac{n} {{n - 1}} \cdot \left[ {u^2 (\varepsilon _m^* ) - u^2 (\varepsilon _m^{} )} \right]} \hfill \\ \end{gathered} $$

(21)

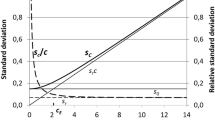
With Eq. (21) the uncertainty value of an additional between-replicate term can be calculated. This is added to all replicates if the uncertainty of the epsilon without the term and the uncertainty of the epsilon with the term are known. The term u(ε _m ) can be calculated from the equivalence check in Eq. (1) under the assumption that the check is just passed.

$$ u^2 (\varepsilon _m^* ) \ge \left( {\frac{{Y_m - \overline Y }} {k}} \right)^2 \quad ({\text{usually }}k = 2) $$

(22)

Combining Eq. (21) and (22) leads to:

$$ u\left( \delta \right) \ge \sqrt {\frac{n} {{n - 1}} \cdot \left[ {\left( {\frac{{Y_m - \overline Y }} {k}} \right)^2 - \, u^2 \left( {Y_m - \overline Y } \right)} \right]} \quad ({\text{usually }}k = 2) $$

(23)

For Y _m the replicate should be selected for which ε _m in respect of k · u(ε _m ) is maximum.