Downstream and upstream oligopolies when retailer’s effort matters

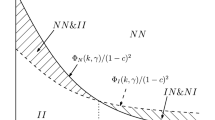
Abstract

This paper investigates the different terms of strategic interactions (non-cooperative, simultaneous move): wholesale versus retail pricing—between Bertrand competing retailers and an upstream oligopoly. The crucial extension is that retailers can play a significant role and this can turn conventional wisdom upside down, e.g.: retail competition need not benefit the upstream firms and wholesale pricing can dominate retail pricing in spite of double marginalization because of the incentives it provides to retailers. In addition, the consequences are investigated of differentiating both pricing instruments either at the downstream (this is motivated by Apple’s entry into the ebook market) or at the upstream level.

Appendix proofs

1.1 Proposition 1 and Corollary 1

The equilibrium follows directly from solving the three first order conditions (14), (16), and (17). Substituting the just computed strategies and elementary simplifications yields,

$$\begin{aligned} p+m-P^{*}=\frac{Ak( 1-\gamma ) ( 1-( 1-\beta ) ( 1-\gamma ) k) }{( 1-2( 1-\beta ) ( 1-\gamma ) k) ( ( 1-\beta ) ( 1-\gamma ) ( 3-\gamma ) k-1) }. \end{aligned}$$

(58)

The denominator is negative for all $k>$ k since the first term of the product must be negative for $k>$ k while the second is positive (again at least for $k>$ k). Therefore the numerator in (58) is negative only for $k>2$ k turning the ratio positive and thus verifies (21).

The comparison with the Bertrand vertically integrated duopoly is less trivial. Considering the difference in retail prices,

$$\begin{aligned} p+m-P^{B}=\frac{Ak( (1-\gamma )-(1-\beta )k) }{( 1-( 1-\beta ) ( 2-\gamma ) k) ( ( 1-\beta ) ( 1-\gamma ) ( 3-\gamma ) k-1) } \end{aligned}$$

(59)

this difference is only positive if the numerator is negative, because as above the denominator is negative due to the first term (the second is the positive one from above). Combining, this leads to the claimed condition ( 22).

Considering the difference in promotions, the comparison with the first best is straightforward due to the same negative denominator as in (58),

$$\begin{aligned} e-e^{*}=\frac{Ak( 1-\beta ) ( 1-\gamma ) ^{2}}{ ( 1-2( 1-\beta ) ( 1-\gamma ) k) ( ( 1-\beta ) ( 1-\gamma ) ( 3-\gamma ) k-1) }<0 \end{aligned}$$

(60)

but less clear cut for the comparison with the Bertrand oligopoly,

$$\begin{aligned} e-e^{B}=\frac{Ak( 1-\beta ) ( \gamma ^{2}-3\gamma +1) }{( 1-( 1-\beta ) ( 2-\gamma ) k) ( ( 1-\beta ) ( 1-\gamma ) ( 3-\gamma ) k-1) }. \end{aligned}$$

(61)

The denominator is the negative one from the above comparison of prices and the last term of the numerator is a quadratic function,

$$\begin{aligned} \gamma ^{2}-3\gamma +1>0\Leftrightarrow \gamma <\frac{( 3-\sqrt{5} ) }{2} \end{aligned}$$

(62)

that is positive for the indicated domain of smaller $\gamma$s.

The computation of the retail monopoly’s profit is straightforward after substituting the equilibrium prices, margins and efforts and the upstream profits are calculated in the same way.

QED.

1.2 Proposition 2

Including the remark, it is necessary to prove that no interior solution $0<s<1$ exists irrespective who controls $s$.

If the upstream firm chooses $s$, as assumed in Proposition 2, the derivatives of its profit functions are,

$$\begin{aligned} \frac{\partial \pi _{i}}{\partial s_{i}^{j}}= & {} P_{i}^{j}q_{i}^{j}>0 \end{aligned}$$

(63)

$$\begin{aligned} \frac{\partial \pi _{i}}{\partial P_{i}^{j}}= & {} s_{i}^{j}q_{i}^{j}+s_{i}^{j}P_{i}^{j}\frac{\partial q_{i}^{j}}{\partial P_{i}^{j}}=2s(A+e-( 1-\beta ) ( 2-\gamma ) P). \end{aligned}$$

(64)

Clearly, no sensible interior solution—equating both equations above to zero, irrespective of the retailer’s effort—can exist. The upstream firm sets its share at the upper bound $s=1$ due the positive derivative (64).

If a retailer can maximize its profit $\pi$ subject to the additional instrument $s_{i}\ge 0$ and defining the Lagrangian,

$$\begin{aligned} L=\pi +\underset{j=a}{\overset{b}{\sum }}\underset{i=1}{\overset{2}{\sum }} \mu _{i}^{j}s_{i}^{j}, \end{aligned}$$

(65)

leads to the following necessary optimality conditions (assuming symmetry on the right hand side):

$$\begin{aligned} \frac{\partial \pi _{i}}{\partial e_{i}}= & {} P_{i}^{j}( 1-s_{i}^{j}) -ke_{i}^{j}=2(( 1-s) P-ke)=0, \end{aligned}$$

(66)

$$\begin{aligned} \frac{\partial \pi _{i}}{\partial s_{i}}= & {} -P_{i}^{j}q_{i}^{j}+\mu _{i}^{j}=-2P(A+e-( 1-\beta ) ( 1-\gamma ) P)+\mu =0, \end{aligned}$$

(67)

$$\begin{aligned} \mu _{i}^{j}s_{i}^{j}= & {} 0,\;\;\;\mu _{i}^{j}\ge 0,\;\;\;s_{i}^{j}\ge 0. \end{aligned}$$

(68)

Substituting the implied optimal effort, $e=( 1-s) P/k$, and symmetry in prices into the share equation yields,

$$\begin{aligned} -2P\left( A+\frac{( 1-s) P}{k}-( 1-\beta ) ( 1-\gamma ) P\right) +\mu =0. \end{aligned}$$

(69)

Therefore, the Kuhn–Tucker multiplier $\mu$ is positive iff sales are positive. Thus the constraint must be binding, $s=0$. This is not surprising given the pure transfer nature of the shares. The retail monopoly’s ability to fix them suggests that it surrenders nothing, i.e., $s=0$, but supports this by the corresponding optimal promotion effort.

The necessary optimality condition for an upstream firm is for any $s_{i}^{j}$ to choose the price that maximizes the profits up and downstream integrated such that $P^{B}$ characterized in (9) results.

Both results extend naturally to oligopolistic retailers.

1.3 Proposition 3

An upstream oligopolist’s profit under retail pricing is given by (29) and here denoted $\pi _{i}( r)$, where the argument $r$ stands for retail pricing. Under wholesale pricing the upstream profit of firm $i$ (the argument $w$ indicates the wholesale pricing arrangement) is

$$\begin{aligned} \pi _{i}( w) =\frac{2A^{2}k^{2}( 1-\beta ) ( 1-\gamma ) ^{2}}{[ 1-( 1-\beta ) ( 1-\gamma ) ( 3-\gamma ) k] ^{2}}. \end{aligned}$$

(70)

Taking the difference

$$\begin{aligned} \pi _{i}( w) -\pi _{i}( r) =\frac{2A^{2}}{( 1-\beta ) }\frac{( 1-( 1-\beta ) ( 1-\gamma ) k) ( ( 1-\beta ) ( 1-\gamma ) ( 5-2\gamma ) k-1) }{( 2-\gamma ) ^{2}( 1-( 1-\beta ) ( 1-\gamma ) ( 3-\gamma ) k) ^{2}}. \end{aligned}$$

(71)

and focussing on the numerator of the second ratio, the first term turns negative for $k>2$ k. This implies the claim because the last term is positive for all $k>$ k. QED.

1.4 Proposition 4

The Nash equilibrium follows immediately from solving the three first order conditions (30)–(32). The upstream $( \pi _{i})$ and downstream $( \pi ^{j})$ profits follow then directly after substituting the equilibrium outcome.

The claims about the wholesale

$$\begin{aligned} p^{a}-p=\frac{Ak\beta ( 1-\gamma ) ( 1-( 1-\beta ) ( 1-\gamma ) k) }{( 1\!-\!\beta ) ( ( 1-\gamma ) ( 3-\beta \!-\!\gamma ) k-1) ( 1-( 1-\beta ) ( 1-\gamma )( 3-\gamma ) k) } \qquad \end{aligned}$$

(72)

and retail price differences between retail monopoly and oligopoly (superscript $a$)

$$\begin{aligned}&p^{a}+m^{a}-( p+m) \nonumber \\&\qquad =-\frac{Ak[ ( 1-\gamma ) ( 1-\beta ) k[ ( 5-2\gamma ) ( 1-\beta ) -1] +2( 1-\beta ) -( \beta -\gamma ) ] }{( 1-\beta ) ( ( 1-\gamma ) ( 3-\beta -\gamma ) k-1) ( 1-( 1-\beta ) ( 1-\gamma ) ( 3-\gamma ) k) } \qquad \quad \end{aligned}$$

(73)

follow because the denominator is negative due to

$$\begin{aligned} ( 1-\gamma ) ( 3-\beta -\gamma ) k-1>\frac{( 1-\gamma ) ( 3-\beta -\gamma ) }{2( 1-\beta ) ( 1-\gamma ) }-1=\frac{2( 1-\beta ) +1-\gamma }{ 2( 1-\beta ) }-1>0, \end{aligned}$$

(74)

and

$$\begin{aligned} 1-( 1-\beta ) ( 1-\gamma )( 3-\gamma ) k<1- \frac{3-\gamma }{2}<0. \end{aligned}$$

(75)

Computation of the upstream profits facing a retail duopoly are,

$$\begin{aligned} \pi _{i}=\frac{2A^{2}k^{2}( 1-\gamma ) ^{2}}{( 1-\beta ) (( 1-\gamma ) ( 3-\beta -\gamma ) k-1) ^{2}}, \end{aligned}$$

(76)

and subtracting that from (70), i.e. the profit of upstream firm $i$ if facing a retail monopoly, yields,

$$\begin{aligned} \Delta \pi _{i}=-\frac{2A^{2}k^{2}\beta ( 1\!-\!\gamma ) ^{2}( ( 1\!-\!\beta ) ( 1\!-\!\gamma ) k\!-\!1) ( 2\!-\!\beta -( 1\!-\!\beta ) ( 1\!-\!\gamma ) ( 6\!-\!\beta \!-\!2\gamma ) k) }{( 1\!-\!\beta ) ( ( 1-\gamma ) ( 3-\beta -\gamma ) k-1) ^{2}( 1-( 1-\beta ) ( 1-\gamma ) ( 3-\gamma ) k) ^{2}}. \end{aligned}$$

(77)

The denominator is negative, the last term in the numerator is definitely negative and the sign of the term in the middle is positive iff $k>2$ k, which verifies this claim.

Taking the differences in demand between oligopolistic and monopolistic retailer yields a fairly similar expression,

$$\begin{aligned} \Delta q_{i}=\frac{Ak[ \gamma +(1-2\gamma )\beta -(1-\beta )(1-\gamma )( (3-\gamma )\gamma +(1-2\gamma )\beta ) k] }{( ( 1-\gamma ) ( 3-\beta -\gamma ) k-1) ( 1-( 1-\beta ) ( 1-\gamma ) ( 3-\gamma ) k) }, \end{aligned}$$

(78)

which verifies the claim because the numerator is positive for $k$ satisfying (38) and (by recall), the denominator is negative since it is $(1-\beta )$ times the denominator in (73).

QED.

1.5 Proposition 6

Departing from the corner equilibrium, $s=1$ and $e^{b}=0$, the first order conditions of the upstream firms are with respect to the wholesale,

$$\begin{aligned} A+e^{a}-( 1-\gamma ) m-( 2-\gamma ) p+( 2-\gamma ) \beta P=0 \end{aligned}$$

(79)

and the retail price

$$\begin{aligned} A+\beta [ ( 2-\gamma ) p+( 1-\gamma ) m] -( 2-\gamma ) P=0 \end{aligned}$$

(80)

The corresponding conditions for retailer $a$ ($b$ has no leverage in this set up) concerning the margin

$$\begin{aligned} A+e^{a}-2( 1-\gamma ) m-( 1-\gamma ) p+( 1-\gamma ) \beta P=0, \end{aligned}$$

(81)

while effort follows from the usual condition,

$$\begin{aligned} m-ke=0. \end{aligned}$$

(82)

Solving all four conditions yields the claimed equilibrium.

Substituting this solution into the profit of retailer $a$ yields (46). Taking the difference in retail prices confirms the claim since,

$$\begin{aligned} p+m-P=\frac{A( 1+( 1+\beta ) k) }{( 1+\beta ) ( 2-\gamma ) ( ( 1-\gamma ) ( 3-\gamma ) k-1) }>0. \end{aligned}$$

(83)

Computation of the sales,

$$\begin{aligned} q_{i}^{a}=\frac{Ak( 1-\gamma ) }{( 1-\gamma ) ( 3-\gamma ) k-1},\;q_{i}^{b}=\frac{A( ( 1-\gamma ) ( 3+\beta -\gamma ) k-1) }{( 2-\gamma ) ( ( 1-\gamma ) ( 3-\gamma ) k-1) }, \end{aligned}$$

(84)

and taking the difference

$$\begin{aligned} q_{i}^{a}-q_{i}^{b}=\frac{A( ( 1-\gamma ) ( 1+\beta ) k-1) }{( 2-\gamma ) ( ( 1-\gamma ) ( 3-\gamma ) k-1) } \end{aligned}$$

(85)

verifies the condition (45).

QED.

1.6 Proposition 7

Starting upstream, assuming the corner equilibrium, $s=1$ and $e_{2}^{j}=0$, and a symmetric outcome, the first order conditions of $i=1$ setting the wholesale price is,

$$\begin{aligned} A+e-( 1-\beta ) m-( 2-\beta ) p+( 1-\beta ) \gamma P=0, \end{aligned}$$

(86)

and correspondingly for $i=2$ for setting its retail price,

$$\begin{aligned} A+( 1-\beta ) ( \gamma ( p+m) -2P) =0. \end{aligned}$$

(87)

The corresponding conditions for the two retailers are confined to choose margins and efforts for product $i=1$ only,

$$\begin{aligned} A+e-( 2-\beta ) m-( 1-\beta ) p+( 1-\beta ) \gamma P=0 \end{aligned}$$

(88)

$$\begin{aligned} m-ke=0. \end{aligned}$$

(89)

Solving all four conditions for $( p,P,m,e)$ yields the equilibrium in Proposition 7.

Substitution of this equilibrium (including the corner solution elements) yields the profits (55) and (56). Taking the difference,

$$\begin{aligned} \pi _{1}-\pi _{2}=\frac{-1+2( 3-\beta +\gamma ( 2-\beta ) ) k-(1-\beta )(1+\gamma )( 5-\beta +\gamma ( 3-\beta ) ) k^{2}}{(1-\beta )((6-2\gamma ^{2}-\beta (2-\gamma ^{2}))k-2)^{2}} \end{aligned}$$

(90)

results in quadratic polynomial which is positive at k and thus turns negative at the second a larger root, which is the one given in ( 57).

QED.