Extended JKR theory on adhesive contact of coated spheres

Abstract

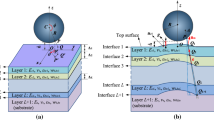
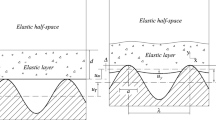
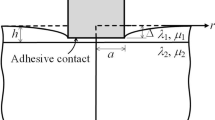
Thin films, coatings, and layered structures are ubiquitous in contemporary micro- and nanoelectronics, optoelectronics, and electromechanical systems, for which adhesion between heterogeneous materials is one of the important mechanical properties to be considered in fabrication and operation. In this study, the adhesive contact between elastic layered spheres, which includes a thin film on a flat substrate as a special case, is analyzed on the basis of the conventional Johnson–Kendall–Roberts (JKR) theory on adhesive contact between elastic spheres. Firstly, the force–depth relations of axisymmetric flat and spherical indentations on an elastic film perfectly bonded to an elastic half-space are obtained in compact forms, depending on two Dundurs parameters and the ratio of the contact radius to the thickness of the film. The solution of a spherical indentation on a layered half-space is then superposed, following a Hertz analysis, to obtain the adhesionless Hertzian contact between the elastic films coated on the elastic spheres. Similarly, the solution to the adhesive JKR contact state between elastic films coated on elastic spheres is also obtained by properly superposing the linear elastic solutions of the flat and spherical indentations on a layered half-space. The obtained Hertzian and adhesive JKR contact states should be regarded as approximate solutions, since the pressure distribution in the contact region does not exactly satisfy Newton’s third law. The JKR state equations among the normalized applied force, normalized penetration depth, and normalized contact radius are obtained in compact forms, in which non-dimensional multiplying factors depending on the geometric parameters and two sets of non-dimensional Dundurs parameters account for the effect of the elastic layers. Finally, the pull-off force at the moment of debonding of the two elastic films coated on the elastic spheres is calculated and compared with the conventional JKR result.

Appendix: Solution procedure of the axisymmetric indentation problem

In order to solve the indentation problem defined in Sect. 2.1, the same solution procedure as that used by Lebedev and Ufliand [17] is adopted here. The Hankel transform and its inverse transform of the order $\rho$, defined as

$$\begin{aligned} B^{[\rho ]}(\lambda ,z)= & {} \int \limits _0^\infty {b(r,z)rJ^{[\rho ]}(\lambda r)\mathrm{d}r}, \end{aligned}$$

(A.1)

$$\begin{aligned} b(r,z)= & {} \int \limits _0^\infty {B^{[\rho ]}(\lambda ,z)\lambda J^{[\rho ]}(\lambda r)\mathrm{d}\lambda }, \end{aligned}$$

(A.2)

respectively, are used, where $J^{[\rho ]}(\lambda r)$ is the $\rho$th-order Bessel function of the first kind. Before proceeding to the solution procedure, every quantity of the length dimension is normalized by the radius a of the indenter tip, and the tilt $({}^{\sim })$ is adopted to indicate the non-dimensionalized quantity, e.g., $\tilde{r}=r/a$ and $\tilde{z}=z/a$. Using the Hankel transform of the first order on $\tilde{u}(\tilde{r},\tilde{z})$ and the zero order on $\tilde{w}(\tilde{r},\tilde{z})$ and $\varepsilon (\tilde{r},\tilde{z})$, we transform Eqs. (1)–(4) as follows:

$$\begin{aligned}&\left( {\frac{\partial ^{2}}{\partial \tilde{z}^{2}}-\lambda ^{2}} \right) U^{[1]}(\lambda ,\tilde{z})=\frac{\lambda }{1-2\nu }E^{[0]}(\lambda ,\tilde{z}), \end{aligned}$$

(A.3)

$$\begin{aligned}&\left( {\frac{\partial ^{2}}{\partial \tilde{z}^{2}}-\lambda ^{2}} \right) W^{[0]}(\lambda ,\tilde{z})=-\frac{1}{1-2\nu }\frac{\partial E^{[0]}(\lambda ,\tilde{z})}{\partial \tilde{z}}, \end{aligned}$$

(A.4)

$$\begin{aligned}&\frac{\partial W^{[0]}(\lambda ,\tilde{z})}{\partial \tilde{z}}+\lambda U^{[1]}(\lambda ,\tilde{z})=E^{[0]}(\lambda ,\tilde{z}), \end{aligned}$$

(A.5)

$$\begin{aligned}&\left( {\frac{\partial ^{2}}{\partial \tilde{z}^{2}}-\lambda ^{2}} \right) E^{[0]}(\lambda ,\tilde{z})=0. \end{aligned}$$

(A.6)

The above system of linear second-order ordinary differential equations has a general solution of the following form:

$$\begin{aligned} U_1^{[1]} (\lambda ,\tilde{z})= & {} \left[ {(\lambda \tilde{z}+\kappa _1 )A_a (\lambda )+B_a (\lambda )} \right] e^{\lambda \tilde{z}}-\left[ {(\lambda \tilde{z}-\kappa _1 )A_b (\lambda )+B_b (\lambda )} \right] e^{-\lambda \tilde{z}}, \end{aligned}$$

(A.7)

$$\begin{aligned} W_1^{[0]} (\lambda ,\tilde{z})= & {} -\left[ {\lambda \tilde{z}A_a (\lambda )+B_a (\lambda )} \right] e^{\lambda \tilde{z}}-\left[ {\lambda \tilde{z}A_b (\lambda )+B_b (\lambda )} \right] e^{-\lambda \tilde{z}}, \end{aligned}$$

(A.8)

$$\begin{aligned} E_1^{[0]} (\lambda ,\tilde{z})= & {} (\kappa _1 -1)\lambda \left[ {A_a (\lambda )e^{\lambda \tilde{z}}+A_b (\lambda )e^{-\lambda \tilde{z}}} \right] , \end{aligned}$$

(A.9)

$$\begin{aligned} U_2^{[1]} (\lambda ,\tilde{z})= & {} -\left[ {(\lambda \tilde{z}-\kappa _2 )A_c (\lambda )+B_c (\lambda )} \right] e^{-\lambda \tilde{z}}, \end{aligned}$$

(A.10)

$$\begin{aligned} W_2^{[0]} (\lambda ,\tilde{z})= & {} -\left[ {\lambda \tilde{z}A_c (\lambda )+B_c (\lambda )} \right] e^{-\lambda \tilde{z}}, \end{aligned}$$

(A.11)

$$\begin{aligned} E_2^{[0]} (\lambda ,\tilde{z})= & {} (\kappa _2 -1)\lambda A_c (\lambda )e^{-\lambda \tilde{z}}, \end{aligned}$$

(A.12)

where $\kappa =3-4\nu$ and the unknown coefficients, $A_a (\lambda )$, $A_b (\lambda )$, $A_c (\lambda )$, $B_a (\lambda )$, $B_b (\lambda )$, and $B_c (\lambda )$ should be determined based on the prescribed boundary conditions. The stresses $\sigma ^{rz}(\tilde{r},\tilde{z})$ and $\sigma ^{zz}(\tilde{r},\tilde{z})$ are expressed in terms of the Hankel-transformed variables $U^{[1]}(\lambda ,\tilde{z})$, $W^{[0]}(\lambda ,\tilde{z})$, and $E^{[0]}(\lambda ,\tilde{z})$ as

$$\begin{aligned} \sigma ^{rz}(\tilde{r},\tilde{z})= & {} \mu \left( {\frac{\partial \tilde{u}}{\partial \tilde{z}}+\frac{\partial \tilde{w}}{\partial \tilde{r}}} \right) =\mu \int \limits _0^\infty {\left[ {\frac{\partial U^{[1]}(\lambda ,\tilde{z})}{\partial \tilde{z}}-\lambda W^{[0]}(\lambda ,\tilde{z})} \right] \lambda J^{[1]}(\lambda \tilde{r})d\lambda }, \end{aligned}$$

(A.13)

$$\begin{aligned} \sigma ^{zz}(\tilde{r},\tilde{z})= & {} 2\mu \left( {\frac{\nu \varepsilon }{1-2\nu }+\frac{\partial \tilde{w}}{\partial \tilde{z}}} \right) =2\mu \int \limits _0^\infty {\left[ {\frac{\nu }{1-2\nu }E^{[0]}(\lambda ,\tilde{z})+\frac{\partial W^{[0]}(\lambda ,\tilde{z})}{\partial \tilde{z}}} \right] \lambda J^{[0]}(\lambda \tilde{r})d\lambda }. \end{aligned}$$

(A.14)

By applying the Hankel transform to Eqs. (5)–(7) and using Eqs. (6) and (A.10) together with Eqs. (A.7) and (A.8), we obtain

$$\begin{aligned}&(1+\kappa _1 )\left[ {A_a (\lambda )-A_b (\lambda )} \right] +2B_a (\lambda )+2B_b (\lambda )=0, \end{aligned}$$

(A.15)

$$\begin{aligned}&\frac{1-\beta _{12} }{\alpha _{12} -\beta _{12} }A_a (\lambda )e^{2\lambda \tilde{h}}+(2\lambda \tilde{h}-\kappa _1 )A_b (\lambda )+2B_b (\lambda )=0, \end{aligned}$$

(A.16)

$$\begin{aligned}&(2\lambda \tilde{h}+\kappa _1 )A_a (\lambda )-\frac{\alpha _{12} +\beta _{12} }{1+\beta _{12} }A_b (\lambda )e^{-2\lambda \tilde{h}}+2B_a (\lambda )=0. \end{aligned}$$

(A.17)

By applying the inverse Hankel transform to Eq. (A.8) with Eqs. (A.12)–(A.14) and substituting it in the first relation of Eq. (5), we obtain

$$\begin{aligned} \int \limits _0^\infty {D(\lambda )J_0 (\lambda \tilde{r})\mathrm{d}\lambda } =\tilde{\delta }-\tilde{\psi }(r) \,\, (\tilde{r}<1). \end{aligned}$$

(A.18)

in which $D(\lambda )=-\lambda \left[ {B_a (\lambda )+B_b (\lambda )} \right]$. In addition, on substituting Eqs. (A.11)–(A.14) in the second relation of Eq. (5), we obtain

$$\begin{aligned} \int \limits _0^\infty {\frac{D(\lambda )\lambda }{1-G(\lambda )}J^{[0]}(\lambda \tilde{r})d\lambda } =0 \,\, (\tilde{r}>1) \end{aligned}$$

(A.19)

where

$$\begin{aligned} G(\lambda )=\frac{\frac{\alpha _{12} -\beta _{12} }{1-\beta _{12} }(1+2\lambda \tilde{h})^{2}+\frac{\alpha _{12} +\beta _{12} }{1+\beta _{12} }-2\frac{\alpha _{12}^2 -\beta _{12}^2 }{1-\beta _{12}^2 }e^{-2\lambda \tilde{h}}}{\frac{\alpha _{12} -\beta _{12} }{1-\beta _{12} }(1+4\lambda ^{2}\tilde{h}^{2})+\frac{\alpha _{12} +\beta _{12} }{1+\beta _{12} }-e^{2\lambda \tilde{h}}-\frac{\alpha _{12}^2 -\beta _{12}^2 }{1-\beta _{12}^2 }e^{-2\lambda \tilde{h}}}. \end{aligned}$$

(A.20)

The solution $D(\lambda )$ of the dual integral Eqs. (A.15) and (A.16) is sought in the form

$$\begin{aligned} D(\lambda )=\frac{2\tilde{\delta }}{\pi }\left[ {1-G(\lambda )} \right] \int \limits _0^1 {\varphi (t)\cos \lambda tdt} \end{aligned}$$

(A.21)

where $\varphi (t)$ is an unknown function; this function and its derivative are continuous in the closed interval [0, 1]. The integral equation (A.16) is then identically satisfied, and integral equation (A.15) can be rewritten as the following Fredholm integral equation of the second kind:

$$\begin{aligned} \varphi (s)-\frac{1}{\pi }\int \limits _0^1 {\varphi (t)\left[ {G_F (t+s)+G_F (t-s)} \right] dt} =\varPsi (s), \,\, (0\le s\le 1) \end{aligned}$$

(A.22)

in which $G_F (t)$ is the Fourier cosine transform of $G(\lambda )$, which is defined as

$$\begin{aligned} G_F (t)=\int \limits _0^\infty {G(\lambda )\cos (\lambda t)} \mathrm{d}\lambda , \end{aligned}$$

(A.23)

and

$$\begin{aligned} \varPsi (s)=1-\frac{s}{\tilde{\delta }}\int \limits _0^{\pi /2} {\frac{\mathrm{d}\tilde{\psi }}{\mathrm{d}s}(as\sin \theta )d\theta }. \end{aligned}$$

(A.24)

The integral equation (A.19) for $\varphi (s)$ can be numerically solved for a given shape of the axisymmetric tip, i.e., the given shape function $\tilde{\psi }(r)$.

For a rigid flat tip, $\tilde{\psi }(r)=0$. Thus, the integral equation (A.19) with $\varPsi (s)=1$ can be solved for $\varphi (s)$, the solution of which is designated by $\varphi _f (s)$. For a rigid spherical tip, $\tilde{\psi }(r)={\tilde{r}^{2}}/{2\tilde{R}}$, where R is the radius of the spherical tip, and thus, $\varPsi (s)=1-{s^{2}}/{\tilde{\delta }\tilde{R}}$. The solution of the integral equation (A.19) can then be expressed as

$$\begin{aligned} \varphi _s (s)=\varphi _f (s)+\frac{\varphi _q (s)}{\tilde{\delta }\tilde{R}}. \end{aligned}$$

(A.25)

Here, $\varphi _f (s)$ is the solution for a flat tip, i.e., the solution to integral equation (A.19) with $\varPsi (s)=1$, and $\varphi _q (s)$ satisfies

$$\begin{aligned} \varphi _q (s)-\frac{1}{\pi }\int \limits _0^1 {\varphi _q (t)\left[ {G_F (t+s)+G_F (t-s)} \right] \mathrm{d}t} =-s^{2} \,\, (0\le s\le 1). \end{aligned}$$

(A.26)

The continuity condition for the normal stress at the boundary of the contact area imposes a constraint on the solution given by Eq. (A.22) [19]:

$$\begin{aligned} \varphi _s (1)=\varphi _f (1)+\frac{\varphi _q (1)}{\tilde{\delta }\tilde{R}}=0, \end{aligned}$$

(A.27)

which provides the relation between the indentation depth $\delta$ and radius a of the contact area for a spherical indentation.