Abstract
A finite element (FE) model for the dimple/gimbal interface of a hard disk drive is developed as a function of normal load, friction coefficient, material properties and dimple geometry. The air bearing force is approximated as a normal load acting on the slider. A rotational acceleration was applied to the dimple to simulate accessing of a hard disk drive suspension during seeking. Results for the relative displacement between the dimple and the gimbal are determined for a typical suspension as a function of normal load, rotational acceleration, friction coefficient, material properties and geometrical parameters of suspension and flexure.
Similar content being viewed by others
1 Introduction
Numerical and experimental results show that fretting wear of the dimple/gimbal interface is likely to generate wear particles and can cause failure of hard disk drives (HDDs) during seeking, track following and load/unload. The lateral displacement of a hard disk drive suspension over the disk can induce a time-dependent small-amplitude relative motion between the dimple and the gimbal. This relative motion can generate fretting wear at the dimple/gimbal interface, resulting in the formation of adhering or loose wear particles. To simulate and reduce fretting wear, it is important to obtain the relative displacement and the stress distribution at the interface of dimple and gimbal. In addition, wear particles can also be produced at the dimple/gimbal interface during the load/unload process. Examination of failed hard disk drives performed by Lee et al. (2004) has shown that small wear particles are likely to be responsible for failure of hard disk drives. Only a few investigations can be found that deal with wear and contact mechanics issues of the dimple/gimbal interface. Li et al. (2009) numerically studied the effect of geometry and material properties of the dimple/gimbal interface on the contact pressure between dimple and gimbal, and showed that contact between the dimple and the gimbal can be modeled as contact between a solid sphere and a rigid flat. Li et al. (2010) investigated the load–displacement behavior of a stainless steel dimple against a rigid sapphire gimbal using a nano-indenter. They found that the asperities of the dimple surface deform plastically and are “flattened” after a number of load/unload cycles. The plastically deformed asperities can generate wear particles and damage hard disk drives. Raeymaekers et al. (2010) investigated fretting wear of the dimple/gimbal interface experimentally and observed that the energy dissipated between the dimple and the gimbal is a function of operating conditions and material properties. In the study of Raeymaekers et al. (2010), the amplitude of the reciprocating motion of the gimbal was chosen to be three microns. However, in an actual hard disk drive the relative displacement between the dimple and the gimbal is different for seeking, track following and ramp load/unloading. Several studies have been made to investigate the response of the dimple/gimbal interface during non-operational shock events, e.g., Murthy et al. (2007) and Zheng et al. (2010). However, no studies can be found in the literature for the magnitude of the relative displacement between the dimple and the gimbal during seeking, operational shock or ramp load/unload motion. Only one investigation is available in the open literature for determining the slip between dimple and flexure for the special case of ramp loading (Lee et al. 2009). In this investigation, the base of the suspension arm was fixed and an impact force was applied to the suspension lift-tab to simulate the ramp contact.
The main goal of this work is to obtain the relative displacement, which is important to understand the mechanism and reduce the fretting wear, between the dimple and the gimbal under different operational condition, such as seeking, track following and load/unload. In the present study, a numerical model for a typical suspension assembly used in a hard disk drive is implemented to investigate the relative displacement between the dimple and the gimbal in LS-Dyna, which is a commercial finite element analysis package. The effect of normal load, rotational acceleration, friction coefficient, material properties and geometrical parameters of suspension and flexure on the relative displacement is determined numerically.
2 Numerical model
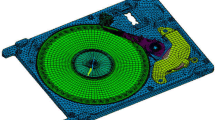
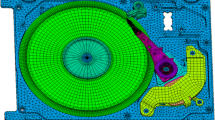
A finite element (FE) model (Fig. 1) was developed, consisting of the actuator, the suspension, the flexure and the slider of a hard disk drive. The geometry of the model was first created in SolidWorks, a commercially available computer aided design software. Then, the model was imported into HyperMesh, a commercially available finite element preprocessor, for discretization and application of boundary conditions. The slider was modeled using solid elements while all other components were simulated with constant thickness shell elements, e.g., the thicknesses of suspension, flexure and actuator arm are 30, 20 and 100 μm, respectively. After preprocessing in HyperMesh, the model was analyzed using LS-Dyna, a commercially available finite element transient solver (LS-DYNA Keyword User’s Manual 2007).
The dimple was modeled as a spherical shell. The mesh over the dimple area was highly refined to obtain the relative displacement between the dimple and the gimbal (see Fig. 1). The surface-to-surface contact pair created between dimple and gimbal was calculated using the penalty method (LS-DYNA Keyword User’s Manual 2007). The contact stiffness was chosen to be the minimum value of the stiffness of the two contact parts. The air bearing force was simplified as a constant normal load acting on the center of the slider. The velocity of the dimple on the suspension was increased in the circumferential direction from zero to a maximum velocity V max during 1 ms, corresponding to accelerations in the range from 120 to 1,970 m/s2.
Figure 2 shows a typical case studied. We first apply a normal load of P = 25 mN during a period of 3 ms. Then, the rotational velocity is applied during 1 ms, from V = 0 to V = 0.4 m/s, corresponding to an acceleration of 400 m/s2. During the velocity application, the load remains constant (see Fig. 2).
The following range of input values was used for the analysis: the normal load P was varied from P = 20 mN to P = 30 mN; the acceleration was evaluated for the range of 120–1,970 m/s2; the Young’s modulus of the dimple was chosen to be in the range from 100 GPa ≤ Ε dimple ≤ 300 GPa; the friction coefficient was varied from 0 ≤ μ ≤ 0.5; the Poison’s ratio was chosen to be ν = 0.31; the dimple was assumed to have values of 55, 75 and 95 nm, and the dimple radius considered was R = 100, 200 and 300 μm. The variation of all the parameters used in this work is according to the requirement of industrial design.
3 Simulation results and discussion
To determine the relative displacement between the dimple and the gimbal for a number of typical load cases, we need to define one point on the dimple and one point on the gimbal and determine the positions of these points as a function of time. Figure 3 shows two adjacent nodes on the dimple/gimbal interface that were selected to determine the relative displacement. We observe that node A is on the dimple while node B is located on the gimbal. The relative motion between the dimple and the gimbal is caused by the acceleration of the suspension which moves in the x–y plane, as shown in Fig. 1. In our model, only the relative displacement between node A and node B in the x–y plane, which was shown in Fig. 1, was evaluated in this study. All values for the relative displacement between node A and node B were determined at a time t = 6 ms after the start of the application of the normal load. The relative displacement presented in this work not only considers the slip between the dimple and the gimbal, the motion of the gimbal due to the pitch and roll of slider was also considered.
3.1 The effect of normal load
To study the effect of the normal load on the relative displacement between the dimple and the gimbal, the normal load was varied from 20 to 30 mN keeping all other parameters constant. The maximum acceleration used in this example equals 120 m/s2. The Young’s modulus of the dimple and gimbal was chosen to be 200 GPa and the Poison’s ratio of the dimple and the gimbal was 0.31. The friction coefficient μ between dimple and gimbal was chosen to be 0.2. The height of the dimple h is 75 μm and the radius of the dimple R equals 200 μm.
Figure 4 shows the relative displacement between the dimple and the gimbal as a function of the normal load. We observe that the relative displacement decreases with increasing normal load. In particular, we note that, the relative displacement decreases by approximately 70% if the load increases by a factor of 1.5. This is due to the fact that the friction force between the dimple and the gimbal for a high normal load is larger than that for a small normal load. Hence, the dimple is less likely to slip for a large normal load.
3.2 The effect of acceleration of the suspension
To study the effect of acceleration on the relative motion between the dimple and the gimbal, we increased the linear velocity of the suspension from zero to a final value in 1 ms keeping all other parameters constant.
Figure 5 presents the relative displacement between the dimple and the gimbal as a function of acceleration. It is apparent that the relative displacement increases by roughly 20 times as the acceleration increases from 120 to 1,970 m/s2.
3.3 The effect of suspension and flexure material properties
Suspensions are made of stainless steel, with a Young’s modulus of approximately 200 GPa. To study the sensitivity of the relative displacement between dimple and gimbal on material properties, we changed the Young’s modules of the suspension from 100 to 300 GPa keeping the Young’s modulus of the flexure at 200 GPa. All other design parameters were kept constant. Results for the relative displacement between the dimple and the gimbal as a function of the Young’s modulus of the suspension and the flexure are shown in Figs. 6 and 7, respectively.
We observe that an increase in the Young’s modulus of the suspension from 100 to 300 GPa leads to an approximately 16% decrease in the relative displacement. However, the relative displacement increases with an increase in the Young’s modulus of the flexure. This is because the stiffness of the whole suspension assembly is changed if one changes either the Young’s modulus of the suspension or the flexure.
3.4 The effect of dimple geometry
Figure 8 shows the parameters controlling the design of the dimple used in our study, i.e., dimple radius (R) and dimple height (h).
Figure 9 shows the relative displacement between the dimple and the gimbal as a function of the dimple radius. The effect of dimple height on the relative displacement between the dimple and the gimbal is shown in Fig. 10.
We observe from Fig. 9 that the relative displacement between dimple and gimbal increases with an increase in the dimple radius. In particular, the relative displacement is found to increase from 100 to 500 nm if the radius of the dimple varies from 100 to 300 μm. On the other hand, an increase in the height of the dimple causes a reduction of the relative displacement at the dimple/gimbal interface.
The reason for these results is that a larger dimple radius or a smaller dimple height leads to lower contact pressure at the dimple/gimbal interfaces for a given normal load. Hence, it is easier to generate relative motion between the dimple and the gimbal if the contact pressure is small.
3.5 The effect of friction coefficient
Figure 11 shows the relative displacement between the dimple and the gimbal as a function of the coefficient of friction. It is apparent that an increase in the friction coefficient reduces the relative displacement since a high friction coefficient is related to a high frictional force at the dimple/gimbal interface for a given normal load. A high frictional force causes reduced slip motion between the dimple and the gimbal. However, it can be seen from Fig. 11 that the change of the relative displacement as a function of the friction coefficient is <3% when the coefficient of friction increases by a factor of four. Thus, the friction coefficient has little effect on the relative displacement between the dimple and the gimbal.
4 Conclusion
This paper investigates the effect of normal load, rotational acceleration, material properties and design parameters of suspension and gimbal on the relative displacement between the dimple and the gimbal. The following conclusions can be drawn from this study:
-
1.
Increasing the normal load between the dimple and the gimbal reduces the relative displacement. Therefore, a high normal load is helpful in reducing fretting wear between the dimple/gimbal interface.
-
2.
The relative displacement between the dimple and the gimbal is a function of the acceleration of the suspension.
-
3.
The relative displacement between dimple and gimbal decreases if the Young’s modulus of the suspension increases. On the other hand, the relative displacement increases when the Young’s modulus of the flexure increases.
-
4.
An increase in the dimple radius tends to increase the relative displacement at the dimple/gimbal interface and, therefore, is likely to causes more wear particles to be generated at the interface.
-
5.
An increase in the dimple height will reduce the relative displacement at the dimple/gimbal interface.
-
6.
The friction coefficient between the dimple and the gimbal has little effect on the relative displacement.
References
Lee DY, Hwang J, Bae GN (2004) Effect of disk rotational speed on contamination particles generated in a hard disk drive. Microsyst Technol 10:103–108
Lee Y, Kim S, Kim K, Park N, Park Y, Kim C, Park K (2009) Analysis of interaction between dimple and flexure by ramp contact. In: The magnetic recording conference, Tuscaloosa, USA, pp 81–82
Li L, Etsion I, Fanslau EB, Talke FE (2009) An analysis of the dimple/gimbal contact in a hard disk drive suspension. In: Proceedings of IIP/ISPS Joint MIPE 2009, Yokohama, Japan, pp 105–106
Li L, Ovcharenko A, Etsion I, Talke FE (2010) The effect of asperity flattening during cyclic normal loading of a rough spherical contact. Tribol Lett 40(3):347–355
LS-DYNA Keyword User’s Manual (2007) version 971, Livermore Software Technology Corporation, Livermore, CA
Murthy AN, Pfabe M, Xu J, Talke FE (2007) Dynamic response of 1-in. form factor disk drives to external shock and vibration loads. Microsyst Technol 13:1031–1038
Raeymaekers B, Helm S, Brunner R, Fanslau EB, Talke FE (2010) Investigation of fretting wear at the dimple/gimbal interface in a hard disk drive suspension. Wear 268:1347–1353
Zheng H, Murthy A, Fanslau EB, Talke FE (2010) Effect of suspension design on the non-operational shock response in a load/unload hard disk drive. Microsyst Technol 16:267–271
Acknowledgments
We would like to thank Mr. Hanya-san of NHK International Corp. for his interest in this study. L. Li thanks the China Scholarship Council (CSC) and Prof. G. Zhang from Harbin Institute of Technology, for supporting his Ph.D. studies at UCSD.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Li, L., Zheng, H., Fanslau, E.B. et al. A numerical study of the dimple/gimbal interface in a hard disk drive. Microsyst Technol 17, 869–873 (2011). https://doi.org/10.1007/s00542-011-1271-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00542-011-1271-5