A Hamiltonian formulation of causal variational principles

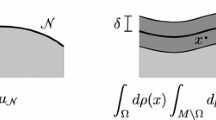
Abstract

Causal variational principles, which are the analytic core of the physical theory of causal fermion systems, are found to have an underlying Hamiltonian structure, giving a formulation of the dynamics in terms of physical fields in space-time. After generalizing causal variational principles to a class of lower semi-continuous Lagrangians on a smooth, possibly non-compact manifold, the corresponding Euler–Lagrange equations are derived. In the first part, it is shown under additional smoothness assumptions that the space of solutions of the Euler–Lagrange equations has the structure of a symplectic Fréchet manifold. The symplectic form is constructed as a surface layer integral which is shown to be invariant under the time evolution. In the second part, the results and methods are extended to the non-smooth setting. The physical fields correspond to variations of the universal measure described infinitesimally by one-jets. Evaluating the Euler–Lagrange equations weakly, we derive linearized field equations for these jets. In the final part, our constructions and results are illustrated in a detailed example on $\mathbb {R}^{1,1} \times S^1$ where a local minimizer is given by a measure supported on a two-dimensional lattice.

Appendix: The Fréchet manifold structure of \({\mathcal {B}}\)

As in Sect. 3 we assume that $\mathscr {F}$ is a smooth manifold of dimension $m \ge 1$. We want to endow the set ${\mathcal {B}}$ with the structure of a Fréchet manifold. The first step is to specify the topology on the set ${\mathcal {B}}$ in (3.7). We choose the compact-open topology defined as follows. First, parametrizing the measures according to (3.6) by a pair $(f, F) \in C^\infty (\mathscr {F}, \mathbb {R}) \times C^\infty (\mathscr {F}, \mathscr {F})$, we can identify ${\mathcal {B}}$ with a subset of the space of such pairs,

$$\begin{aligned} {\mathcal {B}}\subset C^\infty (\mathscr {F}, \mathbb {R}) \times C^\infty (\mathscr {F}, \mathscr {F}). \end{aligned}$$

Our task is to endow the sets $C^\infty (\mathscr {F}, \mathbb {R})$ and $C^\infty (\mathscr {F}, \mathscr {F})$ with the structure of a Fréchet manifold. Once this has been accomplished, the Fréchet structure on ${\mathcal {B}}$ can be introduced simply by assuming that ${\mathcal {B}}$ is a Fréchet submanifold of the product manifold $C^\infty (\mathscr {F}, \mathbb {R}) \times C^\infty (\mathscr {F}, \mathscr {F})$.

Being a vector space, the space $C^\infty (\mathscr {F}, \mathbb {R})$ can be endowed even with the structure of a Fréchet space. To this end, on $\mathscr {F}$ we choose an at most countable atlas $(x_\lambda , U_\lambda )_{\lambda \in \Lambda }$ (with an index set $\Lambda \subset \mathbb {N}$) whose charts $x_\lambda : U_\lambda \rightarrow \mathbb {R}^m$ are defined on relative compact subsets $U_\lambda \subset \mathscr {F}$. We then consider the Fréchet topology induced by the $C^k$-norms in these charts, i.e.

$$\begin{aligned} \big \Vert f \big \Vert _{k,\lambda } := \big \Vert f \circ x_\lambda ^{-1} \big \Vert _{C^k(x_\lambda (U_\lambda ))}. \end{aligned}$$

The resulting topology is metrizable. It is induced for example by the distance function

$$\begin{aligned} d(f,g) := \sum _{k=0}^\infty \;\sum _{\lambda \in \Lambda } \,2^{-k-\lambda }\, \arctan \big \Vert f -g \big \Vert _{k,\lambda }. \end{aligned}$$

In order to endow $C^\infty (\mathscr {F}, \mathscr {F})$ with the structure of a Fréchet manifold, we work locally in a neighborhood of a point $F \in C^\infty (\mathscr {F}, \mathscr {F})$. First, we refine the previous atlas $(x_\lambda , U_\lambda )$ in such a way that the domains $U_\lambda$ are all convex geodesic neighborhoods with respect to a chosen Riemannian metric g on $\mathscr {F}$. Moreover, we further refine this atlas to a new atlas $(y_\gamma , V_\gamma )_{\gamma \in \Gamma }$ in such a way that F maps the domains of the new charts to domains of the old charts, meaning that for every $\gamma \in \Gamma$ there is $\lambda (\gamma ) \in \Lambda$ such that

$$\begin{aligned} F(V_\gamma ) \subset U_{\lambda (\gamma )} \end{aligned}$$

(for example, one can choose the domains of the new charts as open subsets of the sets $U_\lambda \cap F^{-1}(U_\nu )$ for $\lambda , \nu \in \Lambda$ and introduce the charts as the restrictions of $x_\lambda$ to the new domains). We restrict attention to mappings G which are so close to F that they map to the same charts, i.e.

$$\begin{aligned} G(V_\gamma ) \subset U_{\lambda (\gamma )} \qquad \text {for all}~\gamma \in \Gamma . \end{aligned}$$

(5.12)

For such mappings, we can define the $C^k$-norms by

$$\begin{aligned} \big \Vert G - F\big \Vert _{k, \gamma } = \big \Vert x_{\lambda (\gamma )} \circ G \circ y_\gamma ^{-1} - x_{\lambda (\gamma )} \circ F \circ y_\gamma ^{-1} \big \Vert _{C^k(y_\gamma (V_\gamma ))}. \end{aligned}$$

The resulting Fréchet topology is again metrizable, as becomes obvious for example by setting

$$\begin{aligned} d(F,G)&= \left\{ \begin{array}{ll} 4 &{} \text {if}~(5.12) \text { is violated} \\ \displaystyle \sum _{k=0}^\infty \;\sum _{\gamma \in \Gamma } \,2^{-k-\lambda }\, \arctan \Vert F-G \Vert _{k,\gamma } &{} \text {if}~(5.12) \text { holds}. \end{array} \right. \end{aligned}$$

It remains to construct a local chart around F. To this end, it suffices to consider mappings G which satisfy (5.12). Then, since the domains of the charts $U_\lambda$ are all geodesically convex, for any $x \in \mathscr {F}$ there is a unique vector $v(x) \in T_{F(x)} \mathscr {F}$ with the property that $G(x) = \exp _{F(x)} v(x)$. In this way, the mapping G can be described uniquely by a vector field $v \in C^\infty (F(\mathscr {F}), T\mathscr {F})$ on $\mathscr {F}$ along $F(\mathscr {F})$. The mapping $G \rightarrow v$ is the desired chart, taking values in the linear space $C^\infty (F(\mathscr {F}), T\mathscr {F})$.

For clarity, we finally explain what the tangent vectors of ${\mathcal {B}}$ are, how these tangent vectors act on functions, and how these derivatives are related to the derivative $\nabla _{\mathfrak {u}}$ as defined in (3.4). These elementary facts are also needed for the computation of the exterior derivative $d\gamma$ in the proof of Lemma 3.4. Given $\mathfrak {v}=(b,v) \in T_\rho {\mathcal {B}}$, we let $\tilde{\rho }_\tau$ be a smooth curve in ${\mathcal {B}}$ with $\tilde{\rho }_\tau |_{\tau = 0}=\rho$ and $\dot{\rho }_\tau |_{\tau =0} = \mathfrak {v}$. We again write the measures $\tilde{\rho }_\tau$ in the form (3.10) (see Lemma 3.2), so that (3.11) holds. Then the directional derivative of a smooth function $\phi$ on ${\mathcal {B}}$ is defined as usual by

$$\begin{aligned} \mathfrak {v}\phi = \frac{d}{d\tau } \phi \big (\tilde{\rho }_\tau \big ) \big |_{\tau =0}. \end{aligned}$$

In particular, the derivative of $\gamma (\mathfrak {u})$ as defined in (3.21) is given by

$$\begin{aligned} \mathfrak {v}\gamma (\mathfrak {u})\big |_{\tilde{\rho }}&= \frac{d}{d\tau } \int _{\Omega _{N_t}} d\rho \int _{M \setminus \Omega _{N_t}} d\rho \, f_\tau (x)\, \nabla _{2,\mathfrak {u}} {\mathcal {L}}\big (F_\tau (x), F_\tau (y)\big )\, f_\tau (y) \Big |_{\tau =0} \\&= \int _{\Omega _{N_t}} d\rho \int _{M \setminus \Omega _{N_t}} d\rho \, \big ( \nabla _{\mathfrak {v}(x)} + \nabla _{\mathfrak {v}(y)} \big ) \nabla _{2,\mathfrak {u}} {\mathcal {L}}(x, y) . \end{aligned}$$

We point out that here the derivative $\nabla _{\mathfrak {v}(y)}$ also acts on the jet $\mathfrak {u}$ in the derivative $\nabla _{2,\mathfrak {u}}$. The commutator of such products of derivatives can be computed with the help of the following lemma.

Lemma 5.10

For $\mathfrak {u}, \mathfrak {v}\in T_\rho {\mathcal {B}}$, we have

$$\begin{aligned} \nabla _{[\mathfrak {u}, \mathfrak {v}]} = \big [ \nabla _\mathfrak {u}, \nabla _\mathfrak {v}\big ]. \end{aligned}$$

(5.13)

Proof

Again denoting  $\mathfrak {u}=(a,u)$ and $\mathfrak {v}=(b,v)$, for any smooth function $\eta$ on $\mathscr {F}$ we have

$$\begin{aligned} \nabla _\mathfrak {u}\nabla _\mathfrak {v}\eta (x)&= \big ( a(x) + D_u \big ) \big ( b(x) + D_v \big ) \eta (x) \qquad \text {and} \end{aligned}$$

(5.14)

$$\begin{aligned} \big [\nabla _\mathfrak {u}, \nabla _\mathfrak {v}\big ] \eta (x)&= D_{[u,v]} \eta (x) + (D_u b)(x)\, \eta (x) - (D_v a)(x)\, \eta (x). \end{aligned}$$

(5.15)

In order to compute the commutator $[\mathfrak {u}, \mathfrak {v}]$, we consider diffeomorphisms $\Phi _\tau , \tilde{\Phi }_s : {\mathcal {B}}\rightarrow {\mathcal {B}}$ along the vector fields $\mathfrak {u}$ and $\mathfrak {v}$, i.e.

$$\begin{aligned} \Phi _0 = \text {id},\quad \partial _\tau \Phi _\tau = \mathfrak {u}\circ \Phi _\tau \qquad \text {and} \qquad \tilde{\Phi }_0 = \text {id},\quad \partial _s \tilde{\Phi }_s = \mathfrak {v}\circ \tilde{\Phi }_s. \end{aligned}$$

Then

$$\begin{aligned} \int _\mathscr {F}\eta (x)\, d \big (\Phi _\tau \tilde{\Phi }_s \rho \big ) (x)&= \int _\mathscr {F}f_\tau (x)\, \eta \big (F_\tau (x) \big ) \,d \big (\tilde{\Phi }_s \rho \big )(x) \\&= \int _\mathscr {F}\tilde{f}_s(x) \, f_\tau \big (\tilde{F}_s(x) \big )\, \eta \Big (F_\tau \big (\tilde{F}_s(x) \big ) \Big ) \,d \rho (x) \end{aligned}$$

Differentiating with respect to s and $\tau$ at $\tau =s=0$ gives

$$\begin{aligned} \int _\mathscr {F}\eta (x)\, d \big (\mathfrak {u}\mathfrak {v}\rho \big ) (x)&= \frac{d^2}{d\tau ds} \int _\mathscr {F}\eta (x)\, d \big (\Phi _\tau \tilde{\Phi }_s \rho \big ) (x) \bigg |_{s=\tau =0} \\&= \frac{d^2}{d\tau ds} \int _\mathscr {F}\tilde{f}_s(x) \, f_\tau \big (\tilde{F}_s(x) \big )\, \eta \Big (F_\tau \big (\tilde{F}_s(x) \big ) \Big ) \,d \rho (x) \bigg |_{s=\tau =0} \\&= \int _\mathscr {F}\Big ( a(x) \,b(x) + (D_v a)(x) \Big )\, \eta (x)\, d\rho (x)\\&\quad + \int _\mathscr {F}\Big ( b(x)\, (D_u\eta )(x) + a(x)\, (D_v\eta )(x) \Big ) d\rho (x) \\&\quad + \int _\mathscr {F}D_v D_u \eta (x) \, d\rho (x). \end{aligned}$$

Likewise, exchanging the two diffeomorphism gives the vector $\mathfrak {v}\mathfrak {u}\rho$. Hence

$$\begin{aligned} \int _\mathscr {F}\eta (x)\, d \big ([\mathfrak {u}, \mathfrak {v}] \rho \big ) (x) = \int _\mathscr {F}\Big ( D_{[v, u]} \eta + (D_v a)\, \eta - (D_u b)\, \eta \Big ) d\rho (x), \end{aligned}$$

(5.16)

This shows that

$$\begin{aligned}{}[\mathfrak {u}, \mathfrak {v}] = \big ( D_u b - D_v a \, , [u, v] \big ). \end{aligned}$$

Comparing with (5.15) and the definition of $\nabla _{\mathfrak {u}}$ in (3.4) gives (5.13).

We finally note for clarity that the minus sign in (5.16) arises because jets $\mathfrak {u}, \mathfrak {v}$ act on functions on ${\mathcal {B}}$, whereas the derivatives $\nabla _\mathfrak {u}$ and $\nabla _\mathfrak {v}$ act on functions on M. When rewriting compositions of jets $\mathfrak {u}\mathfrak {v}$ as compositions of derivatives on M, the order of the composition is interchanged to $\nabla _v \nabla _u$. $\square$