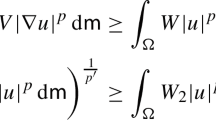Characterization of n-rectifiability in terms of Jones’ square function: part I

Abstract

In this paper it is shown that if $\mu$ is a finite Radon measure in ${\mathbb R}^d$ which is n-rectifiable and $1\le p\le 2$, then

$$\begin{aligned} \displaystyle \int _0^\infty \beta _{\mu ,p}^n(x,r)^2\,\frac{dr}{r}<\infty \quad \mathrm{for}\,\, \mu {\text {-}}\mathrm{a.e.}\,\, x\in {\mathbb R}^d, \end{aligned}$$

where

$$\begin{aligned} \displaystyle \beta _{\mu ,p}^n(x,r) = \inf _L \left( \frac{1}{r^n} \int _{\bar{B}(x,r)} \left( \frac{\mathrm{dist}(y,L)}{r}\right) ^p\,d\mu (y)\right) ^{1/p}, \end{aligned}$$

with the infimum taken over all the n-planes $L\subset {\mathbb R}^d$. The $\beta _{\mu ,p}^n$ coefficients are the same as the ones considered by David and Semmes in the setting of the so called uniform n-rectifiability. An analogous necessary condition for n-rectifiability in terms of other coefficients involving some variant of the Wasserstein distance $W_1$ is also proved.

1 Introduction

A set $E\subset {\mathbb R}^d$ is called n-rectifiable if there are Lipschitz maps $f_i:{\mathbb R}^n\rightarrow {\mathbb R}^d$, $i=1,2,\ldots$, such that

$$\begin{aligned} {\mathcal H}^n\biggl ({\mathbb R}^d{\setminus }\bigcup _i f_i({\mathbb R}^n)\biggr ) = 0, \end{aligned}$$

where ${\mathcal H}^n$ stands for the n-dimensional Hausdorff measure. On the other hand, one says that a Radon measure $\mu$ on ${\mathbb R}^d$ is n-rectifiable if $\mu$ vanishes out of an n-rectifiable set $E\subset {\mathbb R}^d$ and moreover $\mu$ is absolutely continuous with respect to ${\mathcal H}^n_E$.

One of the main objectives of geometric measure theory consist in obtaining different characterizations of n-rectifiability. For example, there are classical characterizations in terms of the existence of approximate tangents, in terms of the existence of densities, or in terms of the size of orthogonal projections. For the precise statements and proofs of these nice results the reader is referred to [13].

More recently, the development of quantitative rectifiability in the pioneering works of Jones [10] and David and Semmes [8] has led to the study of the connection between rectifiability and the boundedness of square functions and singular integrals (for instance, see [6, 7, 11, 15]). Many results on this subject deal with the so called uniform n-rectifiability introduced by David and Semmes [9]. One says that $\mu$ is uniformly n-rectifiable if it is n-AD-regular, that is $c^{-1}r^n\le \mu (B(x,r))\le c\,r^n$ for all $x\in \mathrm{supp}\mu , \,r>0$ and some constant $c>0$, and further there exist constants $\theta ,M>0$ so that, for each $x\in \mathrm{supp}\mu$ and $R>0$, there is a Lipschitz mapping g from the n-dimensional ball $B_n(0,r)\subset {\mathbb R}^n$ to ${\mathbb R}^d$ such that g has Lipschitz norm not exceeding M and

$$\begin{aligned} \mu \bigl (B(x,r)\cap g(B_n(0,r))\bigr ) \ge \theta r^n. \end{aligned}$$

To state one of the main result of [8] we need to introduce some additional notation. Given $1<p<\infty$, a closed ball $B \subset {\mathbb R}^d$, and an integer $0<n<d$, let

$$\begin{aligned} \beta _{\mu ,p}^n(B) = \inf _L \left( \frac{1}{r(B)^n} \int _{B} \left( \frac{\mathrm{dist}(y,L)}{r(B)}\right) ^p\,d\mu (y)\right) ^{1/p}, \end{aligned}$$

where the infimum is taken over all the n-planes $L\subset {\mathbb R}^d$. Quite often, given a fixed n, to simplify notation we will drop the exponent n and we will write $\beta _{\mu ,p}(x,r)$ instead of $\beta _{\mu ,p}^n(\bar{B}(x,r))$. The aforementioned result from [8] is the following.

Theorem A

Let $1\le p < 2n/(n-2)$. Let $\mu$ be an n-AD-regular Borel measure on ${\mathbb R}^d$. The measure $\mu$ is uniformly n-rectifiable if and only if there exists some constant $c>0$ such that

$$\begin{aligned} \int _{B(x,r)}\int _0^r \!\beta _{\mu ,p}^n(y,r)^2 \,\frac{dr}{r}\,d\mu (y)\le c\,r^n \quad \mathrm{for\, all}\,\, x\in \mathrm{supp}\,\mu \, \mathrm{and\,\, all}\,\, r>0. \end{aligned}$$

In the case $n=1$, a result analogous to this one in terms of $L^\infty$ versions of the coefficients $\beta _{\mu ,p}$ is also valid, even without the n-AD-regularity assumption on $\mu$, as shown previously by Jones [10] in his traveling salesman theorem in the plane, and by Jones [10] and Okikiolu [16] in ${\mathbb R}^d$.

Other coefficients which involve a variant of the Wasserstein distance $W_1$ in the spirit of the $\beta _{\mu ,p}$’s have been introduced in [18] and have shown to be useful in the study of different questions regarding the connection between uniform n-rectifiability and the boundedness of n-dimensional singular integral operators (see [14, 19], for example). Given two finite Borel measures $\sigma$, $\mu$ on ${\mathbb R}^d$ and a closed ball $B\subset {\mathbb R}^d$, we set

$$\begin{aligned} \mathrm{dist}_B(\sigma ,\mu ):= \sup \Bigl \{ \Bigl |{\textstyle \int f\,d\sigma - \int f\,d\mu }\Bigr |:\,\mathrm{Lip}(f) \le 1,\,\mathrm{supp}(f)\subset B\Bigr \}, \end{aligned}$$

where $\mathrm{Lip}(f)$ stands for the Lipschitz constant of f. We also set

$$\begin{aligned} \alpha _\mu ^n(B)= \frac{1}{r(B)^{n+1}}\,\inf _{a\ge 0,L} \,\mathrm{dist}_{3B}(\mu ,\,a{\mathcal H}^n_{L}), \end{aligned}$$

where ${\mathcal H}^n_{L}$ stands for the restricion of ${\mathcal H}^n$ to L and the infimum is taken over all the constants $a\ge 0$ and all the n-planes L which intersect B. Again we will drop the exponent n and we will write $\alpha _\mu (x,r)$ instead of $\alpha _\mu ^n(\bar{B}(x,r))$ to simplify the notation.

In [18] the following is proved:

Theorem B

Let $\mu$ be an n-AD-regular Borel measure on ${\mathbb R}^d$. The measure $\mu$ is uniformly n-rectifiable if and only if there exists some constant $c>0$ such that

$$\begin{aligned} \int _{B(x,r)}\int _0^r \alpha _{\mu }^n(y,r)^2 \,\frac{dr}{r}\,d\mu (y)\le c\,r^n \quad \mathrm{for\, all}\,\, x\in \mathrm{supp}\,\,\mu \,\, \mathrm{and\,\, all}\,\, r>0. \end{aligned}$$

In recent years there has been considerable interest in the field of geometric measure theory to obtain appropriate versions of Theorems A. and B. which apply to n-rectifiable measures which are not n-AD-regular. The need for such results is specially notorious in the case $n>1$, where there is no analogue of Jones’ traveling salesman mentioned above. The current paper contributes to fill in this gap by means of the following theorem, which provides necessary conditions for n-rectifiability in terms of the $\beta _{\mu ,p}$ coefficients.

Theorem 1.1

Let $1\le p\le 2$. Let $\mu$ be a finite Borel measure in ${\mathbb R}^d$ which is n-rectifiable. Then

$$\begin{aligned} \int _0^\infty \beta _{\mu ,p}^n(x,r)^2\,\frac{dr}{r}<\infty \quad \mathrm{for}\,\, \mu {\text {-}}a.e.\,\, x\in {\mathbb R}^d. \end{aligned}$$

(1.1)

The integral on the left hand side of 1.1 quite often is called Jones’ square function. In the sequel [3] of the present work, by Azzam and the author of the present paper, it is shown that the finiteness of Jones’ square function for $p=2$ implies n-rectifiability. The precise result is the following:

Let $\mu$ be a finite Borel measure in ${\mathbb R}^d$ such that

$$\begin{aligned} 0<\limsup _{r\rightarrow 0}\frac{\mu (B(x,r))}{r^n}<\infty \quad \text{ and }\quad \int _0^\infty \beta _{\mu ,2}^n(x,r)^2\,\frac{dr}{r}<\infty \end{aligned}$$

(1.2)

for $\mu$-a.e. $x\in {\mathbb R}^d$. Then $\mu$ is n-rectifiable.

So we have:

Corollary 1.2

[3] Let $\mu$ be a finite Borel measure in ${\mathbb R}^d$ such that $0<\limsup _{r\rightarrow 0}\frac{\mu (B(x,r))}{r^n}<\infty$ for $\mu$-a.e. $x\in {\mathbb R}^d$. Then $\mu$ is n-rectifiable if and only if

$$\begin{aligned} \int _0^\infty \beta _{\mu ,2}^n(x,r)^2\,\frac{dr}{r}<\infty \qquad \mathrm{for}\,\,\mu {\text {-}}a.e. \,\,x\in {\mathbb R}^d. \end{aligned}$$

(1.3)

In particular, a set $E\subset {\mathbb R}^d$ with ${\mathcal H}^n(E)<\infty$ is n-rectifiable if and only if (1.3) holds for $\mu ={\mathcal H}^n_E$.

The second result that is obtained in the current paper is the following.

Theorem 1.3

Let $\mu$ be a finite Borel measure in ${\mathbb R}^d$ which is n-rectifiable. Then

$$\begin{aligned} \int _0^\infty \alpha _\mu ^n(x,r)^2\,\frac{dr}{r}<\infty \quad \mathrm{for}\,\, \mu {\text {-}}a.e.\,\, x\in {\mathbb R}^d. \end{aligned}$$

This theorem can be considered as a version for non-AD-regular measures of Theorem B. above.

Let us remark that Theorem 1.1 has already been proved by Pajot [17] under the additional assumption that $\mu$ is n-AD-regular, for $1\le p < n/(n-2)$. Further, in the same paper he has obtained the following partial converse:

Theorem C

Let $1\le p< n/(n-2)$. Suppose that $E\subset {\mathbb R}^d$ is compact and that $\mu = {\mathcal H}^n|E$ is finite. If

$$\begin{aligned} \liminf _{r\rightarrow 0}\frac{\mu (B(x,r))}{r^n}>0 \quad \text{ and } \quad \int _0^\infty \beta _{\mu ,p}^n(x,r)^2\,\frac{dr}{r}<\infty \end{aligned}$$

for $\mu$-a.e. $x\in {\mathbb R}^d$, then E is n-rectifiable.

Notice that in the above theorem the lower density $\liminf _{r\rightarrow 0}\frac{\mu (B(x,r))}{r^n}$ is required to be positive, while in 1.2 it is the upper density which must be positive. Recall that the assumption that the upper density is positive $\mu$-a.e. is satisfied for all measures of the form $\mu ={\mathcal H}^n_E$, with ${\mathcal H}^n(E)<\infty$. On the contrary, the lower density may be zero $\mu$-a.e. for this type of measures.

Quite recently, Badger and Schul [5] have shown that Theorem C. also holds for other measures different from Hausdorff measures, namely for Radon measures $\mu$ satisfying $\mu \ll {\mathcal H}^n$. However, their extension of Pajot’s theorem still requires the lower density $\liminf _{r\rightarrow 0}\frac{\mu (B(x,r))}{r^n}$ to be positive $\mu$-a.e.

To describe another previous result of Badger and Schul [4] we need to introduce some additional terminology. We say that $\mu$ is n-rectifiable in the sense of Federer if there are Lipschitz maps $f_i:{\mathbb R}^n\rightarrow {\mathbb R}^d$, $i=1,2,\ldots$, such that

$$\begin{aligned} \mu \biggl ({\mathbb R}^d{\setminus }\bigcup _i f_i({\mathbb R}^n)\biggr ) = 0. \end{aligned}$$

The condition that $\mu$ is absolutely continuous with respect to ${\mathcal H}^n$ is not required.

Given a cube $Q\subset {\mathbb R}^d$, denote

$$\begin{aligned} {\widetilde{\beta }}_{\mu ,2}^n(Q) = \inf _L \left( \frac{1}{\mu (3Q)} \int _{3Q} \left( \frac{\mathrm{dist}(y,L)}{\ell (Q)}\right) ^2\,d\mu (y)\right) ^{1/2}, \end{aligned}$$

where $\ell (Q)$ stands for the side length of Q and the infimum is taken over all n-planes $L\subset {\mathbb R}^d$. The result of Badger and Schul in [4] reads as follows:

Theorem D

If $\mu$ is a locally finite Borel measure on ${\mathbb R}^d$ which is 1-rectifiable in the sense of Federer, then

$$\begin{aligned} \sum _{Q\in {\mathcal D}:x\in Q,\ell (Q)\le 1}{\widetilde{\beta }}_{\mu ,2}^1(Q)^2\,\frac{\ell (Q)}{\mu (Q)}<\infty \quad \mathrm{for}\,\, \mu {\text {-}} a.e.\,\, x\in {\mathbb R}^d, \end{aligned}$$

(1.4)

where ${\mathcal D}$ stands for the lattice of dyadic cubes of ${\mathbb R}^d$.

According to [4], Peter Jones conjectured in 2000 that some condition in the spirit of 1.4 should be necessary and sufficient for n-rectifiability (in the sense of Federer). Observe that from Theorem 1.1 it follows easily that if $\mu$ is n-rectifiable (in the sense that $\mu \ll {\mathcal H}^n$), then

$$\begin{aligned} \sum _{Q\in {\mathcal D}:x\in Q,\ell (Q)\le 1}{\widetilde{\beta }}_{\mu ,2}^n(Q)^2<\infty \quad \mathrm{for}\,\, \mu {\text {-}}\mathrm{a.e.}\,\,x\in {\mathbb R}^d. \end{aligned}$$

(1.5)

Notice that Theorem D. is only proved in the case $n=1$. As remarked by the authors in [4], it is not clear how one could extend their techniques to the case $n>1$. However, in contrast to Theorem 1.1 their result has the advantage that it applies to measures that need not be absolutely continuous with respect to ${\mathcal H}^1$.

For another work in connection with rectifiability and other variants of the $\beta _2$ coefficients, we suggest the reader to see Lerman’s work [12], and for two recent papers which involve some variants of the $\alpha$ coefficients without the AD-regularity assumption, see [1, 2].

The plan of the paper is the following. First we prove Theorem 1.3 in Sect. 2. We carry out this task by combining suitable stopping time arguments with the application of Theorem B. to the particular case when $\mu$ is n-dimensional Hausdorff measure on an n-dimensional Lipschitz graph. Finally, we show in Sect. 3 that Theorem 1.1 follows from Theorem 1.3 by means of other stopping time arguments. Both in Theorems 1.1 and 1.3, the stopping time arguments are mainly used to control the oscillations of the density of $\mu$ at different scales.

In this paper the letters c, C stand for some absolute constants which may change their values at different occurrences. On the other hand, constants with subscripts, such as $c_1$, do not change their values at different occurrences. The notation $A\lesssim B$ means that there is some fixed constant c (usually an absolute constant) such that $A\le c\,B$. Further, $A\approx B$ is equivalent to $A\lesssim B\lesssim A$. We will also write $A\lesssim _{c_1} B$ if we want to make explicit the dependence on the constants $c_1$ of the relationship “$\lesssim$”.

2 The proof of Theorem 1.3

2.1 The main lemma

In this section we will prove the following:

Lemma 2.1

(Main Lemma) Let $\mu$ be a finite Borel measure on ${\mathbb R}^d$ and let $\Gamma \subset {\mathbb R}^d$ be an n-dimensional Lipschitz graph in ${\mathbb R}^d$. Then

$$\begin{aligned} \int _0^\infty \alpha _\mu (x,r)^2\,\frac{dr}{r}<\infty \quad \mathrm{for}\,\, {\mathcal H}^n{\text {-}}a.e. \,\,x\in \Gamma . \end{aligned}$$

It is clear that Theorem 1.3 follows as a corollary of the preceding result, taking into account that if $\mu$ is n-rectifiable, then it is absolutely continuous with respect to ${\mathcal H}^n$ restricted to a countable union of (possibly rotated) n-dimensional Lipschitz graphs.

In the remaining of this section we assume that $\mu$ is a finite Borel measure and $\Gamma$ is an n-dimensional Lipschitz graph, as in Lemma 2.1.

2.2 The exceptional set H

We intend now to define an exceptional set H which will contain the balls centered at $\Gamma$ with too much mass. The precise definition is as follows. Let $M\gg 1$ be some constant to be fixed below. Let $H_0$ be the family of points $x\in \Gamma$ such that there exists a ball B(x, r) such that

$$\begin{aligned} \mu (B(x,r))\ge M\,r^n. \end{aligned}$$

For $x\in H_0$, denote by $r_x$ a radius such that

$$\begin{aligned} \mu (B(x,r_x))\ge M\,r_x^n \qquad \text {and}\qquad \mu (B(x,r))\le M\,r^n \quad \text {for all} \qquad r\ge 2r_x. \end{aligned}$$

(2.1)

By the 5r covering theorem, we can cover $H_0$ by a family of balls $B(x_i,5\,r_{x_i})$, $i\in I_H$, with $x_i\in H_0$, so that the balls $B(x_i,r_{x_i})$, $i\in I_H$, are pairwise disjoint. We denote $\Delta _i = B(x_i,5r_{x_i})$ and we set

$$\begin{aligned} H = H(M) = \bigcup _{i\in I_H} \Delta _i. \end{aligned}$$

Note that

$$\begin{aligned} M \le \frac{\mu (\tfrac{1}{5}\Delta _i)}{r(\tfrac{1}{5}\Delta _i)^n} \le 5^n\, \frac{\mu (\Delta _i)}{r(\Delta _i)^n} \le 5^nM. \end{aligned}$$

(2.2)

Also, observe that any ball B centered on $\Gamma$ which is not contained in H satisfies

$$\begin{aligned} \mu (B)\le M\,r(B)^n. \end{aligned}$$

For technical reasons it is also convenient to introduce the sets $H^k$, for $k\ge 1$:

$$\begin{aligned} H^k = H^k(M) = \bigcup _{i\in I_H} k\Delta _i, \end{aligned}$$

(2.3)

where $k\Delta _i$ is the ball concentric with $\Delta _i$ with radius $k\,r(\Delta _i)$. Obviously, we have $H\subset H^k$.

Lemma 2.2

For any positive integer k, we have

$$\begin{aligned}\lim _{M\rightarrow \infty } {\mathcal H}^n(H^k(M)\cap \Gamma ) = 0. \end{aligned}$$

Proof

For $x\in {\mathbb R}^d$, denote

$$\begin{aligned} {\mathcal M}_n \mu (x) := \sup _{r>0}\frac{\mu (B(x,r))}{r^n}. \end{aligned}$$

Since the ${\mathcal H}^n(B(y,r)\cap \Gamma )\le c\,r^n$ for all $y\in \Gamma$ and all $r>0$, it turns out that ${\mathcal M}_n$ is bounded from the space of real Radon measures $M({\mathbb R}^d)$ to $L^{1,\infty }({\mathcal H}^n_\Gamma )$. See Sect. 2.3 of [20], for example. Then it follows that

$$\begin{aligned} {\mathcal M}_n \mu (x) <\infty \quad \mathrm{for}\,\, {\mathcal H}^n{\text {-}}\mathrm{a.e. }\,\, x\in \Gamma . \end{aligned}$$

(2.4)

Let $x\in H^k$, so that $x\in k\Delta _i$ for some $i\in I_H$. By 2.2 we have

$$\begin{aligned} \frac{\mu (B(x,(k+1)r(\Delta _i))}{((k+1)\,r(\Delta _i))^n} \ge \frac{\mu (\Delta _i)}{((k+1)\,r(\Delta _i))^n} \ge \frac{M}{5^n(k+1)^n}, \end{aligned}$$

and thus ${\mathcal M}_n \mu (x)>10^{-n}M$. Hence we infer that

$$\begin{aligned} H^k\subset \bigl \{x\in {\mathbb R}^d:\,{\mathcal M}_n \mu (x)>5^{-n}\,(k+1)^{-n}M\bigr \}, \end{aligned}$$

and so

$$\begin{aligned} {\mathcal H}^n(H^k(M)\cap \Gamma ) \le {\mathcal H}^n\left( \bigl \{x\in \Gamma :\,{\mathcal M}_n \mu (x)>5^{-n}(k+1)^{-n}M\bigr \}\right) \rightarrow 0 \end{aligned}$$

as $M\rightarrow \infty$, by 2.4. $\square$

From now we will allow the constants c in the estimates below to depend on M.

2.3 The Whitney cubes and the approximating measure $\sigma$

Let $A:{\mathbb R}^n\rightarrow {\mathbb R}^{d-n}$ be the function whose Lipschitz graph is $\Gamma$. Consider now a decomposition of ${\mathbb R}^d{\setminus } \Gamma$ into a family ${\mathcal W}$ of dyadic Whitney cubes. That is, ${\mathcal W}$ is a collection of dyadic cubes with disjoint interiors such that

$$\begin{aligned} \bigcup _{Q\in {\mathcal W}} Q = {\mathbb R}^d{\setminus } \Gamma , \end{aligned}$$

and moreover there are some constants $R>20$ and $D_0\ge 1$ such the following holds for every $Q\in {\mathcal W}$:

• (i) $10Q \subset {\mathbb R}^d{\setminus } \Gamma$;

• (ii) $R Q \cap \Gamma \ne \varnothing$;

• (iii) there are at most $D_0$ cubes $Q'\in {\mathcal W}$ such that $10Q \cap 10Q' \ne \varnothing$. Further, for such cubes $Q'$, we have $\ell (Q')\approx \ell (Q)$.

From the properties (i) and (ii) it is clear that $\mathrm{dist}(Q,\Gamma )\approx \ell (Q)$. We assume that the Whitney cubes are small enough so that

$$\begin{aligned} \mathrm{diam}(Q)< \mathrm{dist}(Q,\Gamma ). \end{aligned}$$

(2.5)

This can be achieved by replacing each cube $Q\in {\mathcal W}$ by its descendants $P\in {\mathcal D}_k(Q)$, for some fixed $k\ge 1$, if necessary. From 2.5 we infer that if $Q\in {\mathcal W}$ intersects some ball B(y, r) with $y\in \Gamma$, then

$$\begin{aligned} \mathrm{diam}(Q)\le r, \end{aligned}$$

(2.6)

and thus

$$\begin{aligned} Q\subset B(y,3r). \end{aligned}$$

(2.7)

We denote ${\mathcal W}_G$ the subfamily of the cubes from ${\mathcal W}$ which are disjoint from H. The subindex G stands for “good”. It is straightforward to check that

$$\begin{aligned} \mu (Q)\le c\,M\,\ell (Q)^n\quad \mathrm{if}\,\,Q\in {\mathcal W}_G. \end{aligned}$$

(2.8)

Notice also that if $Q\in {\mathcal W}{\setminus }{\mathcal W}_G$, then there exists some ball $\Delta _i$, $i\in I_H$, such that $Q\cap \Delta _i\ne \varnothing$, and thus, by 2.6 and 2.7,

$$\begin{aligned} \mathrm{diam}(Q)\le \mathrm{dist}(Q,\Gamma )\le r(\Delta _i)\qquad \text {and}\qquad Q\subset 3\Delta _i. \end{aligned}$$

(2.9)

With each cube $Q\in {\mathcal W}{\setminus }{\mathcal W}_G$ we associate a ball $\Delta _i$ such that $Q\cap \Delta _i\ne \varnothing$, and we write $Q\sim \Delta _i$. The choice does not matter if the ball $\Delta _i$ is not unique.

Lemma 2.3

There exists a family of non-negative functions $g_Q$, for $Q\in {\mathcal W}_G$, which verify the following properties:

• (a) $\mathrm{supp}g_Q\subset \Gamma \cap \bar{B}(x_Q,A\,\ell (Q))$, for some constant A depending at most on n and d.

• (b) $\int g_Q\,d{\mathcal H}^n_{\Gamma } = \mu (Q)$.

• (c) there exists some constant $c_1$ depending at most on n and d such that the function

  $$\begin{aligned} g_0 := \sum _{Q\in {\mathcal W}_G} g_Q \end{aligned}$$

  (2.10)

  satisfies $\Vert g_0\Vert _{L^\infty ({\mathcal H}^n_{\Gamma })}\le c_1\,M.$

Proof

We denote by ${\mathcal W}_G^j$ the cubes from ${\mathcal W}_G$ which have side length $2^{-j}$.

We will construct the functions $g_Q$ as weak limits of other functions $g_Q^k$. For a fixed $k\ge 1$, we set

$$\begin{aligned} g_Q^k =0\quad \text {for}\quad Q\in \bigcup _{j\ge k+1}{\mathcal W}_G^j. \end{aligned}$$

For $j\le k$, we will define the functions $g_Q^j$ inductively, starting with the functions $g_Q^k$ associated with the cubes $Q\in {\mathcal W}_G^k$, then the functions $g_Q^{k}$ associated with the cubes from in ${\mathcal W}_G^{k-1}$, then the functions $g_Q^{k}$ associated with the cubes from ${\mathcal W}_G^{k-2}$, etc.

To define $g_Q^k$ for $Q\in {\mathcal W}_G^k$ we consider the ball

$$\begin{aligned} {\widetilde{B}}_Q = B(x_Q,A\,\ell (Q)), \end{aligned}$$

where A is some absolute constant such that $B(x_Q,\frac{1}{2}A\,\ell (Q))\cap \Gamma \ne \varnothing$, which in particular ensures that

$$\begin{aligned} {\mathcal H}^n(\Gamma \cap {\widetilde{B}}_Q)\ge c^{-1}\,\ell (Q)^n. \end{aligned}$$

(2.11)

Then we define

$$\begin{aligned} g_Q^k = \frac{\mu (Q)}{{\mathcal H}^n(\Gamma \cap {\widetilde{B}}_Q)}\,\chi _{\Gamma \cap {\widetilde{B}}_Q}. \end{aligned}$$

So by 2.11 and the fact that Q is good cube, $\Vert g_Q^k\Vert _{L^\infty ({\mathcal H}^n{\lfloor }\Gamma \cap {\widetilde{B}}_Q)}\le c$, and by the finite superposition of the balls ${\widetilde{B}}_Q$, $Q\in {\mathcal W}_G^k$, we get

$$\begin{aligned} \sum _{Q\in {\mathcal W}_G^k} g_Q^k\le c_2. \end{aligned}$$

(2.12)

Suppose now that we have already defined the functions $g_Q^k$ for the cubes $Q\in {\mathcal W}_G^i$, with $i=k,k-1,\ldots , j$, so that $\mathrm{supp}g_Q^k\subset \Gamma \cap \bar{B}(x_Q,A\,\ell (Q))$ and $\int g_Q^k\,d{\mathcal H}^n_\Gamma =\mu (Q)$. To construct $g_R^k$, for $R\in {\mathcal W}_G^{j-1}$, we consider the set

$$\begin{aligned} E_R = \biggl \{x\in \Gamma \cap {\widetilde{B}}_R:\sum _{j\le i \le k}\, \sum _{Q\in {\mathcal W}_G^i}g_Q^k\le \lambda \biggr \}, \end{aligned}$$

where $\lambda$ is some positive constant to be fixed below. By Chebychev, we have

$$\begin{aligned} {\mathcal H}^n\bigl (\Gamma \cap {\widetilde{B}}_R{\setminus } E_R\bigr ) \le \frac{1}{\lambda }\int _{{\widetilde{B}}_R} \sum _{j\le i \le k}\, \sum _{Q\in {\mathcal W}_G^i}g_Q^k\,d{\mathcal H}^n_\Gamma \le \frac{1}{\lambda }\sum _{j\le i \le k}\, \sum _{\begin{array}{c} Q\in {\mathcal W}_G^i:\\ Q\cap {\widetilde{B}}_R\ne \varnothing \end{array}}\mu (Q). \end{aligned}$$

(2.13)

Since all the cubes $Q\in {\mathcal W}_G^i$ which intersect ${\widetilde{B}}_R$, with $j\le i \le k$, are contained in $t{\widetilde{B}}_R$, where $t>1$ is some absolute constant, we get

$$\begin{aligned} {\mathcal H}^n\bigl (\Gamma \cap {\widetilde{B}}_R{\setminus } E_R\bigr ) \le \frac{1}{\lambda }\,\mu (t{\widetilde{B}}_R). \end{aligned}$$

On the other hand, from 2.13 it is clear that ${\mathcal H}^n\bigl (\Gamma \cap {\widetilde{B}}_R{\setminus } E_R\bigr )$ vanishes unless there exists some good cube $Q_0\in {\mathcal W}_G$ which intersects ${\widetilde{B}}_R$. This implies that

$$\begin{aligned} \mu \bigl (t{\widetilde{B}}_R\bigr )\le c\,M\,t\,\ell (R)^n. \end{aligned}$$

Indeed, if ${\widetilde{B}}_Q'$ is some ball centered on $\Gamma$ which contains $t{\widetilde{B}}_Q$ (and thus $Q_0$) with $r({\widetilde{B}}_Q')\le 2t\,r({\widetilde{B}}_Q)$, then $\mu \bigl (t{\widetilde{B}}_R\bigr )\le \mu ({\widetilde{B}}_Q')\le M\,r({\widetilde{B}}_Q')^n$ because $Q_0\not \subset H$, which proves the claim. Then we deduce that

$$\begin{aligned} {\mathcal H}^n\bigl (\Gamma \cap {\widetilde{B}}_R{\setminus } E_R\bigr ) \le \frac{c\,M\,t}{\lambda }\,\ell (R)^n \le \frac{c_3\,M\,t}{\lambda }\,{\mathcal H}^n(\Gamma \cap {\widetilde{B}}_R). \end{aligned}$$

As a consequence, if we choose $\lambda = 2\,c_3\,M\,t$, we get

$$\begin{aligned} {\mathcal H}^n(E_R)\ge \frac{1}{2}\,{\mathcal H}^n(\Gamma \cap {\widetilde{B}}_R)\ge c\,\ell (R)^n. \end{aligned}$$

(2.14)

We define

$$\begin{aligned} g_R^k = \frac{\mu (R)}{{\mathcal H}^n(E_R)}\,\chi _{E_R}. \end{aligned}$$

From 2.8, we know that $\mu (R)\le c\,\ell (R)^n$, and then from 2.14 it follows that

$$\begin{aligned} g_R^k\le \frac{c\,M\,\ell (R)^n}{\ell (R)^n}\,\chi _{E_R} = c\,\chi _{E_R}. \end{aligned}$$

From the fact that $E_R\subset {\widetilde{B}}_R$, it turns out that the sets $E_R$, for $R\in {\mathcal W}_G^{j-1}$, have finite superposition. Thus,

$$\begin{aligned} \sum _{R\in {\mathcal W}_G^{j-1}} g_R^k\le c_4\,\chi _{\bigcup _{R\in {\mathcal W}_G^{j-1}} E_R}. \end{aligned}$$

On the other hand, by definition

$$\begin{aligned} \sum _{j\le i \le k}\, \sum _{Q\in {\mathcal W}_G^i}g_Q^k(x)\le \lambda \qquad \mathrm{for\,all}\,\,x\in \bigcup _{R\in {\mathcal W}_G^{j-1}} E_R. \end{aligned}$$

Therefore,

$$\begin{aligned} \sum _{j-1\le i \le k}\, \sum _{Q\in {\mathcal W}_G^i}g_Q^k(x)\le \lambda + c_4\qquad \mathrm{for\,all}\,\, x\in \bigcup _{R\in {\mathcal W}_G^{j-1}} E_R. \end{aligned}$$

(2.15)

Notice also that

$$\begin{aligned} \sum _{j-1\le i \le k}\, \sum _{Q\in {\mathcal W}_G^i}g_Q^k(x)= \sum _{j\le i \le k}\, \sum _{Q\in {\mathcal W}_G^i}g_Q^k(x) \qquad \mathrm{for}\,\,x\not \in \bigcup _{R\in {\mathcal W}_G^{j-1}} E_R. \end{aligned}$$

(2.16)

Arguing by induction, from the conditions 2.12, 2.15 and 2.16 it follows easily that the functions $g_Q^k$ satisfy

$$\begin{aligned} \sum _{Q\in {\mathcal W}_G} g_Q^k\le \max \bigl (c_2,c_4+\lambda \bigr ). \end{aligned}$$

To get the functions $g_Q$, $Q\in {\mathcal W}_G$, we will take weak limits in $L^\infty ({\mathcal H}^n_\Gamma )$. Suppose that the cubes from ${\mathcal W}_G$ are ordered, so that ${\mathcal W}_G=\{Q_1,Q_2,\ldots \}$. Consider a partial subsequence $\{g_{Q_1}^k\}_{k\in I_1}\subset \{g_{Q_1}^k\}_{k\ge 1}$ (i.e. $I_1\subset \{k:k\ge 1\}$) which converges weakly to some function $g_{Q_1}\in L^\infty ({\mathcal H}^n_\Gamma )$. Now take another subsequence $\{g_{Q_2}^k\}_{k\in I_2}\subset \{g_{Q_2}^k\}_{k\in I_1}$ which converges weakly to $g_{Q_2}\in L^\infty ({\mathcal H}^n_\Gamma )$, and so on. By construction, the functions $g_Q$, $Q\in {\mathcal W}_G$, satisfy the properties (a) and (b) in the lemma. Also, (c) is fulfilled. Indeed, for any k and any fixed N we have

$$\begin{aligned} \sum _{i=1}^N g_{Q_i}^k\le c. \end{aligned}$$

So letting $k\rightarrow \infty$, we get

$$\begin{aligned} \sum _{i=1}^N g_{Q_i}\le c \end{aligned}$$

uniformly on N, which proves (c). $\square$

Assume that the set $I_H$ defined just above 2.1 equals $\{1,2,\ldots \}$. For $i\in I_H$ we denote

$$\begin{aligned} {\widetilde{\Delta }}_i =\Delta _i \Bigg \backslash \bigcup _{j<i} \Delta _j, \end{aligned}$$

so that

$$\begin{aligned} H= \bigcup _{i\in I_H} {\widetilde{\Delta }}_i \end{aligned}$$

and the sets ${\widetilde{\Delta }}_i$, $i\in I_H$, are pairwise disjoint.

Lemma 2.4

For each $i\in I_H$ there exists a non-negative function $h_i$ which satisfies the following properties:

• (a) $\mathrm{supp}h_i\subset \Gamma \cap \frac{1}{5}\Delta _i$.

• (b) $\int h_i\,d{\mathcal H}^n_{\Gamma } = \mu ({\widetilde{\Delta }}_i\cap \Gamma ) + \sum _{Q\in {\mathcal W}{\setminus }{\mathcal W}_G:Q\sim \Delta _i}\mu (Q)$.

• (c) $\Vert h_i\Vert _{L^\infty ({\mathcal H}^n_{\Gamma })}\le c_5\,M$.

Proof

For $i\in I_H$ we set

$$\begin{aligned} F_i =\bigcup _{Q\in {\mathcal W}{\setminus } {\mathcal W}_G:Q\sim \Delta _i}Q. \end{aligned}$$

If Q is as above, then $Q\subset 3\Delta _i$, by 2.7. Therefore,

$$\begin{aligned} \mu (F_i)\le \mu (3\Delta _i)\lesssim M\,r(\Delta _i)^n\approx M\,{\mathcal H}^n(\Gamma \cap \tfrac{1}{5} \Delta _i). \end{aligned}$$

So if we let

$$\begin{aligned} h_i = \frac{\mu ({\widetilde{\Delta }}_i\cap \Gamma ) + \mu (F_i)}{{\mathcal H}^n(\Gamma \cap \tfrac{1}{5} \Delta _i)}\,\chi _{\Gamma \cap \tfrac{1}{5} \Delta _i}, \end{aligned}$$

the lemma follows. $\square$

We consider the function

$$\begin{aligned} g = g_0 + \sum _{i\in I_H} h_i. \end{aligned}$$

Recall that $g_0$ has been defined in 2.10. Since the functions $h_i$, $i\in I_H$, have disjoint supports, it is clear that

$$\begin{aligned} \Vert g\Vert _{L^\infty ({\mathcal H}^n_{\Gamma })}\le (c_1+c_5)\,M. \end{aligned}$$

We also take the following measure:

$$\begin{aligned} \sigma = \mu {\lfloor }(\Gamma {\setminus } H) + g\,\,{\mathcal H}^n_{\Gamma }. \end{aligned}$$

In a sense, $\sigma$ should be considered as an approximation of $\mu$ which is supported on $\Gamma$.

2.4 The $\alpha$-coefficients of $\mu$ on the good $\Gamma$-cubes

We consider the following “$\Gamma$-cubes” associated with $\Gamma$: we say that $Q\subset \Gamma$ is a $\Gamma$-cube if it is a subset of the form $Q=\Gamma \cap (Q_0\times {\mathbb R}^{d-n})$, where $Q_0\subset {\mathbb R}^n$ is an n-dimensional cube. We denote $\ell (Q):=\ell (Q_0)$. We say that Q is a dyadic $\Gamma$-cube if $Q_0$ is a dyadic cube. The center of Q is the point $x_Q=(x_{Q_0},A(x_{Q_0}))$, where $x_{Q_0}$ is the center of $Q_0$ and $A:{\mathbb R}^n\rightarrow {\mathbb R}^{d-n}$ is the function that defines $\Gamma$. The collection of dyadic $\Gamma$-cubes Q with $\ell (Q)=2^{-j}$ is denoted by ${\mathcal D}_{\Gamma ,j}$. Also, we set ${\mathcal D}_{\Gamma }=\bigcup _{j\in {\mathbb Z}}{\mathcal D}_{\Gamma ,j}$ and ${\mathcal D}_{\Gamma }^k=\bigcup _{j\ge k}{\mathcal D}_{\Gamma ,j}$. We denote by ${\mathcal D}_\Gamma (R)$ the collection of the $\Gamma$-cubes from ${\mathcal D}_\Gamma$ which are contained in R.

The collection of the “good” dyadic $\Gamma$-cubes, which we denote by ${\mathcal D}_\Gamma ^G$, consists of the $\Gamma$-cubes $Q\in {\mathcal D}_\Gamma$ such that

$$\begin{aligned}Q\not \subset \bigcup _{i\in I_H} 9\Delta _i = H^9\end{aligned}$$

(recall the definition of $H^k$ in 2.3). In particular, if $Q\in {\mathcal D}_\Gamma ^G$, then $Q\not \subset H$. We also denote ${\mathcal D}_\Gamma ^G(R)={\mathcal D}_\Gamma (R)\cap {\mathcal D}_\Gamma ^G$.

Given a $\Gamma$-cube Q, we denote by $B_Q$ a closed ball concentric with Q with $r(B_Q)=3\mathrm{diam}(Q)$. Note that $B_Q$ contains Q and is centered on $\Gamma$. We set

$$\begin{aligned} \alpha _\mu (Q) :=\alpha _\mu (B_Q). \end{aligned}$$

The main objective of this subsection is to prove the following.

Lemma 2.5

There exists some constant c such that for every $R\in {\mathcal D}_\Gamma$,

$$\begin{aligned} \sum _{Q\in {\mathcal D}_\Gamma ^G(R)} \alpha _\mu (Q)^2\,\ell (Q)^n\le c\,\ell (R)^n. \end{aligned}$$

Observe that the sum above runs only over the good cubes $Q\in {\mathcal D}_\Gamma ^G(R)$. For the proof we need first a couple of auxiliary results.

Lemma 2.6

Let $Q\in {\mathcal D}_\Gamma ^G$. Let $P\in {\mathcal W}{\setminus }{\mathcal W}_G$ be such that $P\cap B_{Q}\ne \varnothing$. If $P\sim \Delta _i$, then

$$\begin{aligned} \ell (P)\le r(\Delta _i)\le c\,\ell (Q) \end{aligned}$$

(2.17)

and

$$\begin{aligned} P\subset 3\Delta _i\subset 3B_{Q}. \end{aligned}$$

(2.18)

Recall that $P\in {\mathcal W}{\setminus }{\mathcal W}_G$ means that P is a Whitney cube such that $P\cap H \ne \varnothing$, while $Q\in {\mathcal D}_\Gamma ^G$ means that Q is a cube from ${\mathcal D}_\Gamma$ such that $Q\not \subset H^9$.

Proof

The first inequality in 2.17 and the first inclusion in 2.18 have been proved in 2.9.

From the fact that $P\subset 3\Delta _i$ we infer that $3\Delta _i\cap B_{Q}\ne \varnothing$. Suppose that $r(B_{Q})\le r(3\Delta _i)$. This would imply that $B_{Q}\subset 9\Delta _i$ and so $Q\subset 9\Delta _i$, which contradicts the fact that $Q\in {\mathcal D}_\Gamma ^G$. So we deduce that

$$\begin{aligned} r(B_{Q})> r(3\Delta _i), \end{aligned}$$

which implies that $3\Delta _i\subset 3B_{Q}$ and also the second inequality in 2.17. $\square$

Lemma 2.7

If $Q\in {\mathcal D}_\Gamma ^G$, then

$$\begin{aligned} \alpha _\mu (Q)\le \alpha _\sigma (Q) + c\int _{3B_{Q}} \frac{\mathrm{dist}(x,\Gamma )}{\ell (Q)^{n+1}}\, d\mu (x) +c \sum _{i\in I_H:\Delta _i\subset 3B_Q} \left( \frac{r(\Delta _i)}{\ell (Q)}\right) ^{n+1}. \end{aligned}$$

Recall that

$$\begin{aligned} \sigma = \mu {\lfloor }(\Gamma {\setminus } H) + g\,\,{\mathcal H}^n_{\Gamma }. \end{aligned}$$

(2.19)

Proof

Let ${\varphi }$ be a 1-Lipschitz function supported on $B_Q$. Consider $c_Q\ge 0$ and an n-plane $L_Q$ which minimize $\alpha _\sigma (Q)$. Then we write

$$\begin{aligned} \left| \int {\varphi }\,d\mu - c_Q\,\int {\varphi }\,d{\mathcal H}^n_{L_Q}\right| \le \left| \int {\varphi }\,d(\mu -\sigma )\right| + \left| \int {\varphi }\,d(\sigma - c_Q\,{\mathcal H}^n_{L_Q})\right| . \end{aligned}$$

(2.20)

Observe that the last integral on the right hand side does not exceed $\alpha _\sigma (Q)\,\ell (Q)^{n+1}$. To estimate the first term on the right hand side, using 2.19 and 2.10 we set

$$\begin{aligned} \mu -\sigma = \mu {\lfloor }(\Gamma {\setminus } H)^c - g\,{\mathcal H}^n_\Gamma = \mu {\lfloor }(\Gamma {\setminus } H)^c - \sum _{P\in {\mathcal W}_G} g_P\,{\mathcal H}^n_\Gamma - \sum _{i\in I_H} h_i\,{\mathcal H}^n_\Gamma . \end{aligned}$$

As in Lemma 2.4, for $i\in I_H$ we denote

$$\begin{aligned} F_i =\bigcup _{P\in {\mathcal W}:P\sim \Delta _i}P, \end{aligned}$$

and further we set

$$\begin{aligned} {\widetilde{F}}_i = ({\widetilde{\Delta }}_i\cap \Gamma ) \cup F_i. \end{aligned}$$

We split $\mu {\lfloor }(\Gamma {\setminus } H)^c$ as follows:

$$\begin{aligned} \mu {\lfloor }(\Gamma {\setminus } H)^c&= \sum _{P\in {\mathcal W}_G}\mu {\lfloor }P + \sum _{i\in I_H} \mu ({\widetilde{\Delta }}_i\cap \Gamma ) + \sum _{i\in I_H}\,\sum _{P\in {\mathcal W}{\setminus } {\mathcal W}_G: P\sim \Delta _i} \mu {\lfloor }P \\&= \sum _{P\in {\mathcal W}_G}\mu {\lfloor }P + \sum _{i\in I_H}\mu {\lfloor }{\widetilde{F}}_i. \end{aligned}$$

Then we get

$$\begin{aligned} \left| \int {\varphi }\,d(\mu -\sigma )\right|\le & {} \sum _{P\in {\mathcal W}_G}\left| \int {\varphi }\,d(\mu {\lfloor }P- g_P\,{\mathcal H}^n_\Gamma )\right| \nonumber \\&+ \sum _{i\in I_H} \left| \int {\varphi }\,d(\mu {\lfloor }{\widetilde{F}}_i - h_i\,{\mathcal H}^n_\Gamma )\right| . \end{aligned}$$

(2.21)

For each $P\in {\mathcal W}_G$, since $\int g_P\,d{\mathcal H}^n_{\Gamma } = \mu (P)$, we deduce that

$$\begin{aligned} \left| \int {\varphi }\,d(\mu {\lfloor }P- g_P\,{\mathcal H}^n_\Gamma )\right|\le & {} \left| \int _P({\varphi }(x) - {\varphi }(x_P))\,d\mu (x)\right| \\&+ \left| \int ({\varphi }(x_P) - {\varphi }(x))\, g_P(x)\,{\mathcal H}^n_\Gamma (x))\right| . \end{aligned}$$

To deal with the first integral on the right hand side we take into account that for $x\in P$ we have

$$\begin{aligned} |{\varphi }(x) - {\varphi }(x_P)|\le \Vert \nabla {\varphi }\Vert _\infty \,|x-x_P|\le c\,\ell (P). \end{aligned}$$

(2.22)

Concerning the second integral, recall that $\mathrm{supp}g_P\subset \Gamma \cap \bar{B}(x_P,A\,\ell (P))$, and thus we also have $|x-x_P|\le c\,\ell (P)$ in the domain of integration, so that 2.22 holds in this case too. Therefore,

$$\begin{aligned} \left| \int {\varphi }\,d(\mu {\lfloor }P- g_P\,{\mathcal H}^n_\Gamma )\right| \le c\,\ell (P)\,\mu (P)\approx \int _P \mathrm{dist}(x,\Gamma )\,d\mu (x), \end{aligned}$$

where we took into account that $\mathrm{dist}(x,\Gamma )\approx \ell (P)$ for every $x\in P$. Recall that $\mathrm{supp}{\varphi }\subset B_Q$ and thus the integral on the left hand side above vanishes unless $P\cap B_Q\ne \varnothing$. As remarked in 2.7 this ensures that $P\subset 3B_Q$. Hence,

$$\begin{aligned} \sum _{P\in {\mathcal W}_G}\left| \int {\varphi }\,d(\mu {\lfloor }P- g_P\,{\mathcal H}^n_\Gamma )\right| \le c\,\int _{3B_Q} \mathrm{dist}(x,\Gamma )\,d\mu (x). \end{aligned}$$

(2.23)

To estimate the las term on the right hand side of 2.21 we argue analogously. For each $i\in I_H$, we have

$$\begin{aligned} \int h_i\,d{\mathcal H}^n_{\Gamma } = \sum _{Q\in {\mathcal W}{\setminus }{\mathcal W}_G:Q\sim \Delta _i}\mu (Q) + \mu ({\widetilde{\Delta }}_i\cap \Gamma )= \mu ({\widetilde{F}}_i), \end{aligned}$$

and so

$$\begin{aligned} \left| \int {\varphi }\,d(\mu {\lfloor }{\widetilde{F}}_i - h_i\,{\mathcal H}^n_\Gamma )\right|\le & {} \left| \int _{{\widetilde{F}}_i} ({\varphi }(x)-{\varphi }(x_i))\,d\mu (x)\right| \nonumber \\&+ \left| \int ({\varphi }(x_i) - {\varphi }(x))\, h_i(x)\,{\mathcal H}^n_\Gamma (x))\right| . \end{aligned}$$

(2.24)

By 2.4 we know that

$$\begin{aligned} {\widetilde{F}}_i\cup \mathrm{supp}h_i\subset 3\Delta _i \cup \frac{1}{5}\Delta _i \subset 3\Delta _i. \end{aligned}$$

(2.25)

So we have $|{\varphi }(x)-{\varphi }(x_i)|\le c\,r(\Delta _i)$ in the integrals on the right hand side of 2.24 and thus we obtain

$$\begin{aligned} \left| \int {\varphi }\,d(\mu {\lfloor }{\widetilde{F}}_i - h_i\,{\mathcal H}^n_\Gamma )\right| \le c\,r(\Delta _i)\,\mu ({\widetilde{F}}_i). \end{aligned}$$

On the other hand, observe that the left side of 2.24 vanishes unless ${\widetilde{F}}_i\cap B_Q\ne \varnothing$ or $\frac{1}{5}\Delta _i\cap B_Q\ne \varnothing$. The first option implies that

$$\begin{aligned} {\widetilde{F}}_i\subset 3B_Q, \end{aligned}$$

by 2.18. If $\frac{1}{5}\Delta _i\cap B_Q\ne \varnothing$, there exists also some $P\in {\mathcal W}{\setminus }{\mathcal W}_G$ which intersects both $B_Q$ and $\Delta _i$, which implies that $3\Delta _i\subset 3B_Q$ by 2.18 again. Together with 2.25 this yields

$$\begin{aligned} \nonumber \sum _{i\in I_H} \left| \int {\varphi }\,d(\mu {\lfloor }{\widetilde{F}}_i - h_i\,{\mathcal H}^n_\Gamma )\right|\le & {} c\sum _{i:3\Delta _i \subset 3B_Q} r(\Delta _i)\,\mu ({\widetilde{F}}_i) \\\le & {} c\sum _{i:3\Delta _i \subset 3B_Q} r(\Delta _i)\,\mu (3\Delta _i) \nonumber \\\le & {} c\sum _{i:\Delta _i \subset 3B_Q} r(\Delta _i)^{n+1}, \end{aligned}$$

(2.26)

where we took into account that $\mu (3\Delta _i)\le M\,3^n\,r(\Delta _i)^n$ in the last inequality.

From 2.21, 2.23 and 2.26, we derive

$$\begin{aligned} \left| \int {\varphi }\,d(\mu -\sigma )\right| \le c\,\int _{3B_Q} \mathrm{dist}(x,\Gamma )\,d\mu (x) + c\sum _{i:\Delta _i \subset 3B_Q} r(\Delta _i)^{n+1}. \end{aligned}$$

Plugging this estimate into 2.20, we get

$$\begin{aligned} \left| \int {\varphi }\,d\mu - c_Q\,\int {\varphi }\,d{\mathcal H}^n_{L_Q}\right|&\le c\,\int _{3B_Q} \mathrm{dist}(x,\Gamma )\,d\mu (x) \\&\quad + c\sum _{i:\Delta _i \subset 3B_Q} r(\Delta _i)^{n+1} + \alpha _\sigma (Q)\,\ell (Q)^{n+1}. \end{aligned}$$

Taking the supremum over all 1-Lipschitz functions ${\varphi }$ supported on $B_Q$, the lemma follows. $\square$

Proof of lemma 2.5

Obviously we may assume that ${\mathcal D}_\Gamma ^G(R)\ne \varnothing$, which implies that $R\in {\mathcal D}_\Gamma ^G$.

By Lemma 2.7, for any $R\in {\mathcal D}_\Gamma$ we have

$$\begin{aligned} \sum _{Q\in {\mathcal D}_\Gamma ^G(R)} \alpha _\mu (Q)^2\,\ell (Q)^n\le & {} c \sum _{Q\in {\mathcal D}_\Gamma ^G(R)}\alpha _\sigma (Q)^2\,\ell (Q)^n \nonumber \\&+\, c\sum _{Q\in {\mathcal D}_\Gamma ^G(R)} \left( \int _{3B_{Q}} \frac{\mathrm{dist}(x,\Gamma )}{\ell (Q)^{n+1}}\, d\mu (x)\right) ^2\,\ell (Q)^n \nonumber \\&+\,c \sum _{Q\in {\mathcal D}_\Gamma ^G(R)}\left( \sum _{i\in I_H:\Delta _i\subset 3B_Q} \left( \frac{r(\Delta _i)}{\ell (Q)}\right) ^{n+1}\right) ^2\,\ell (Q)^n.\qquad \end{aligned}$$

(2.27)

Recall that

$$\begin{aligned} \sigma = \mu {\lfloor }(\Gamma {\setminus } H) + g\,{\mathcal H}^n_{\Gamma } = \rho \,{\mathcal H}^n_{\Gamma } + g\,\,{\mathcal H}^n_{\Gamma }, \end{aligned}$$

with $\Vert \rho \Vert _{L^\infty ({\mathcal H}^n_{\Gamma })}+ \Vert g\Vert _{L^\infty ({\mathcal H}^n_{\Gamma })}\lesssim 1$, taking into account that $\mu (B(x,r))\le M\,r^n$ for all $x\in \Gamma {\setminus } H$ and all $r>0$. Then, by [18], we have

$$\begin{aligned} \sum _{Q\in {\mathcal D}_\Gamma (R)} \alpha _\sigma (Q)^2\,\ell (Q)^n\le c\,\ell (R)^n. \end{aligned}$$

(2.28)

Let us turn our attention to the last term on the right hand side of 2.27. Using the estimate $r(\Delta _i)\le c\,\ell (Q)$, we derive

$$\begin{aligned} \sum _{i\in I_H:\Delta _i\subset 3B_Q} \left( \frac{r(\Delta _i)}{\ell (Q)}\right) ^{n+1} \le \frac{c}{\ell (Q)^n}\sum _{i\in I_H:\Delta _i\subset 3B_Q} r(\Delta _i)^n \lesssim 1. \end{aligned}$$

Thus,

$$\begin{aligned}&\sum _{Q\in {\mathcal D}_\Gamma ^G(R)}\left( \sum _{i\in I_H:\Delta _i\subset 3B_Q} \biggl (\frac{r(\Delta _i)}{\ell (Q)}\biggr )^{n+1}\right) ^2 \,\ell (Q)^n \\&\qquad \lesssim \sum _{Q\in {\mathcal D}_\Gamma (R)}\,\sum _{i\in I_H:\Delta _i\subset 3B_Q} \left( \frac{r(\Delta _i)}{\ell (Q)}\right) ^{n+1}\,\ell (Q)^n\\&\qquad \lesssim \sum _{i\in I_H:\Delta _i\subset cB_R} r(\Delta _i)^{n+1} \sum _{Q\in {\mathcal D}_\Gamma :3B_Q\supset \Delta _i} \frac{1}{\ell (Q)}. \end{aligned}$$

Since

$$\begin{aligned} \sum _{Q\in {\mathcal D}_\Gamma :3B_Q\supset \Delta _i} \frac{1}{\ell (Q)}\lesssim \frac{1}{r(\Delta _i)}, \end{aligned}$$

we deduce that

$$\begin{aligned} \sum _{Q\in {\mathcal D}_\Gamma ^G(R)}\left( \sum _{i\in I_H:\Delta _i\subset 3B_Q} \biggl (\frac{r(\Delta _i)}{\ell (Q)}\biggr )^{n+1}\right) ^2 \,\ell (Q)^n \lesssim \!\sum _{i\in I_H:\Delta _i\subset cB_R} r(\Delta _i)^n \lesssim \ell (R)^n, \end{aligned}$$

taking into account that the balls $\frac{1}{5}\Delta _i$, $i\in I_H$, are disjoint.

To estimate the second term on the right side of 2.27 we use Cauchy-Schwarz:

$$\begin{aligned} \left( \int _{3B_{Q}} \frac{\mathrm{dist}(x,\Gamma )}{\ell (Q)^{n+1}}\, d\mu (x)\right) ^2\le \mu (3B_Q) \int _{3B_{Q}} \left( \frac{\mathrm{dist}(x,\Gamma )}{\ell (Q)^{n+1}}\right) ^2\, d\mu (x). \end{aligned}$$

Since $Q\in {\mathcal D}_\Gamma ^G$, we have $\mu (3B_Q)\le c\ell (Q)^n$, and so the right hand side of the above inequality does not exceed

$$\begin{aligned} c\int _{3B_{Q}} \frac{\mathrm{dist}(x,\Gamma )^2}{\ell (Q)^{n+2}}\, d\mu (x). \end{aligned}$$

Therefore,

$$\begin{aligned}&\sum _{Q\in {\mathcal D}_\Gamma ^G(R)} \biggl (\int _{3B_{Q}} \frac{\mathrm{dist}(x,\Gamma )}{\ell (Q)^{n+1}}\, d\mu (x)\biggr )^2\,\ell (Q)^n \\&\qquad \le c\sum _{Q\in {\mathcal D}_\Gamma ^G(R)} \int _{3B_{Q}} \frac{\mathrm{dist}(x,\Gamma )^2}{\ell (Q)^{2}}\, d\mu (x). \end{aligned}$$

By Fubini, the term on the right hand side equals

$$\begin{aligned} \int _{c_6B_R}\mathrm{dist}(x,\Gamma )^2\sum _{Q\in {\mathcal D}_\Gamma ^G(R)}\chi _{3B_{Q}}(x)\, \frac{1}{\ell (Q)^{2}} \, d\mu (x), \end{aligned}$$

since

$$\begin{aligned} \bigcup _{Q\in {\mathcal D}_\Gamma (R)} 3B_{Q}\subset c_6B_R \end{aligned}$$

for some constant $c_6>1$. Notice now that

$$\begin{aligned} \sum _{Q\in {\mathcal D}_\Gamma ^G(R)}\chi _{3B_{Q}}(x)\, \frac{1}{\ell (Q)^2} = \sum _{Q\in {\mathcal D}_\Gamma ^G: x\in 3B_{Q}, Q\subset R} \frac{1}{\ell (Q)^2} \lesssim \frac{1}{\mathrm{dist}(x, \Gamma )^2}, \end{aligned}$$

because the condition $x\in 3B_{Q}$ implies that $\mathrm{dist}(x,\Gamma )\le r(B_Q)\approx \ell (Q)$. Thus,

$$\begin{aligned} \sum _{Q\in {\mathcal D}_\Gamma ^G(R)} \biggl (\int _{3B_{Q}} \frac{\mathrm{dist}(x,\Gamma )}{\ell (Q)^{n+1}}\, d\mu (x)\biggr )^2\,\ell (Q)^n&\lesssim \int _{c_6B_R} \frac{\mathrm{dist}(x,\Gamma )^2}{\mathrm{dist}(x,\Gamma )^2} \, d\mu (x) \\&= \mu (c_6B_R)\le c\,\ell (R)^n. \end{aligned}$$

The last inequality follows from the fact that $R\in {\mathcal D}_\Gamma ^G$, and so R is not contained in $H^9$, and thus neither in H. Hence $B(x_R,\mathrm{diam}(c_6 R))\not \subset H$ and then

$$\begin{aligned} \mu (c_6B_R)\le M\,r(c_6 B_R)^n\le c\,M\,\ell (R)^n. \end{aligned}$$

We have shown that the three terms on the right hand side of 2.27 are bounded by $c\,\ell (R)^n$, and so we are done. $\square$

2.5 Proof of the main Lemma 2.1

We claim that for any $R\in {\mathcal D}_\Gamma$,

$$\begin{aligned} \int _{R{\setminus } H^9(M)}\int _0^{\ell (R)} \alpha _\mu (x,r)^2\,\frac{dr}{r}\, d{\mathcal H}^n_\Gamma (x) \le c(M)\,\ell (R)^n. \end{aligned}$$

(2.29)

This follows from the fact that given $x\in R{\setminus } H^9$ and $r\le \ell (R)$, there exists some cube $Q\in {\mathcal D}^G_\Gamma (R)$ with $\ell (Q)\approx r$ such that $B(x,r)\subset B_Q$, and so

$$\begin{aligned} \alpha _\mu (x,r)\lesssim \alpha _\mu (Q). \end{aligned}$$

Then we obtain

$$\begin{aligned} \int _{R{\setminus } H^9(M)}\int _0^{\ell (R)} \alpha _\mu (x,r)^2\,\frac{dr}{r}\, d{\mathcal H}^n_\Gamma (x)\lesssim \sum _{Q\in {\mathcal D}_\Gamma ^G(R)} \alpha _\mu (Q)^2\,\ell (Q)^n. \end{aligned}$$

By Lemma 2.5, the right hand side above does not exceed $c(M)\,\ell (R)^n$, and thus we get 2.29. In particular, this estimate ensures that

$$\begin{aligned} \int _0^{\ell (R)} \alpha _\mu (x,r)^2\,\frac{dr}{r}<\infty \quad \mathrm{for}\,\, {\mathcal H}^n{\text {-}}\mathrm{a.e.}\,\,\ x\in R{\setminus } H^9(M). \end{aligned}$$

It easily follows then that

$$\begin{aligned} \int _0^{\infty } \alpha _\mu (x,r)^2\,\frac{dr}{r}<\infty \quad \mathrm{for}\,\, {\mathcal H}^n{\text {-}}\mathrm{a.e.}\,\,x\in R{\setminus } H^9(M). \end{aligned}$$

By Lemma 2.2, ${\mathcal H}^n(H^9(M)\cap \Gamma )\rightarrow 0$ as $M\rightarrow \infty$ and thus the preceding estimate holds ${\mathcal H}^n$-a.e. in R. As $R\in {\mathcal D}_\Gamma$ is arbitrary, we are done. $\square$

3 The proof of Theorem 1.1

3.1 Peliminaries

The case $p=1$ of Theorem 1.1 follows from the fact that

$$\begin{aligned} \beta _{\mu ,1}(x,r)\le c\,\alpha _\mu (x,2r) \quad \mathrm{for\,all}\,\, x\in \mathrm{supp}\,\,\mu , r>0. \end{aligned}$$

(3.1)

To see this, take an n-plane $L\subset {\mathbb R}^d$ and $a\ge 0$ which minimize $\alpha _\mu (x,2r)$, let ${\varphi }$ be a Lipschitz function supported on $\bar{B}(x,2r)$ which equals 1 on $\bar{B}(x,r)$, with $\mathrm{Lip}({\varphi })\le 1/r$. Then

$$\begin{aligned} \int _{\bar{B}(x,r)}\mathrm{dist}(y,L)\,d\mu (y)&\le \int _{\bar{B}(x,r)}{\varphi }(y)\,\mathrm{dist}(y,L)\,d\mu (y)\\&= \left| \int {\varphi }(y)\,\mathrm{dist}(y,L)\,d(\mu - a {\mathcal H}^n_L)(y)\right| \\&\le \mathrm{Lip}\bigl ({\varphi }\,\mathrm{dist}(\cdot ,L)\bigr )\,\mathrm{dist}_{2B}(\mu , a {\mathcal H}^n_L)\\&\le c\,r^{n+1}\,\alpha _\mu (x,2r), \end{aligned}$$

which yields 3.1.

Notice also that, for $1\le p<2$, given a ball B(x, r) and any n-plane L, by Hölder’s inequality we have

$$\begin{aligned}&\frac{1}{r^n} \int _{\bar{B}(x,r)} \left( \frac{\mathrm{dist}(y,L)}{r}\right) ^p\,d\mu (y)\\&\quad \le \left( \frac{1}{r^n}\int _{\bar{B}(x,r)} \left( \frac{\mathrm{dist}(y,L)}{r}\right) ^2\,d\mu (y)\right) ^{p/2} \left( \frac{\mu (\bar{B}(x,r))}{r^n}\right) ^{1-p/2}. \end{aligned}$$

So taking infimums and raising to the power 1 / p, we obtain

$$\begin{aligned} \beta _{\mu ,p}(x,r)\le \left( \frac{\mu (\bar{B}(x,r))}{r^n}\right) ^{\frac{1}{p}-\frac{1}{2}}\,\beta _{\mu ,2}(x,r). \end{aligned}$$

As a consequence, for all $x\in {\mathbb R}^d$,

$$\begin{aligned} \int _0^\infty \beta _{\mu ,p}(x,r)^2\,\frac{dr}{r} \le \left( \sup _{r>0} \frac{\mu (\bar{B}(x,r))}{r^n}\right) ^{\frac{2}{p}-1} \int _0^\infty \beta _{\mu ,2}(x,r)^2\,\frac{dr}{r}. \end{aligned}$$

If $\mu$ is a finite Borel measure which is rectifiable, then the supremum on the right hand side above is finite for $\mu$-a.e. $x\in {\mathbb R}^d$. So to prove Theorem 1.1 it suffices to show that

$$\begin{aligned} \int _0^\infty \beta _{\mu ,2}(x,r)^2\,\frac{dr}{r}<\infty \quad \mathrm{for}\,\, \mu {\text {-}}\mathrm{a.e.}\,\, x\in {\mathbb R}^d. \end{aligned}$$

(3.2)

To prove this statement we will follow an argument inspired by some techniques from [18, Lemma 5.2], where it is shown that the $\beta _{\mu ,2}$’s can be estimated in terms of the $\alpha _\mu$ coefficients when $\mu$ is an n-dimensional AD-regular measure. In the present situation, $\mu$ fails to be AD-regular (in general) and so we will need to adapt the techniques in [18] by suitable stopping time arguments.

3.2 The stopping cubes

We denote by ${\mathcal D}$ the family of dyadic cubes from ${\mathbb R}^d$. Also, given $R\in {\mathcal D}$, ${\mathcal D}(R)$ stands for the cubes from ${\mathcal D}$ which are contained in R.

Since $\mu$ is n-rectifiable, the density

$$\begin{aligned} \Theta ^{n}(x,\mu )= \lim _{r\rightarrow 0}\frac{\mu (B(x,r))}{(2r)^n} \end{aligned}$$

exists and is positive $\mu$-almost everywhere. So, given $R\in {\mathcal D}$ with $\mu (R)>0$ and ${\varepsilon }>0$, there exists $N>0$ big enough such that

$$\begin{aligned} \mu \left( \{x\in R:\,N^{-1}\le \Theta ^n(x,\mu )\le N\}\right) > (1-{\varepsilon })\,\mu (R). \end{aligned}$$

Let $r_0>0$ and denote now

$$\begin{aligned} A = A(N,r_0) ={\{x\in R: \,N^{-1}\,r^n\le \mu (B(x,r))\le 4N\,r^n\,\,\mathrm{for}\,\,0<r\le r_0\}}. \end{aligned}$$

Then we infer that

$$\begin{aligned} \mu (R{\setminus } A)\le 2{\varepsilon }\end{aligned}$$

if $r_0$ is small enough.

By Theorem 1.3 we know that

$$\begin{aligned} \int _0^\infty \alpha _\mu (x,r)^2\,\frac{dr}{r}<\infty . \end{aligned}$$

So setting

$$\begin{aligned} F = F(N) = \left\{ x\in R\cap \mathrm{supp}\,\,\mu : \,\displaystyle \int _0^\infty \alpha _\mu (x,r)^2\,\frac{dr}{r}\le N\right\} , \end{aligned}$$

it turns out that

$$\begin{aligned} \mu (R{\setminus } F)\le {\varepsilon }\,\mu (R) \end{aligned}$$

if N is big enough.

We take N and $r_0$ so that

$$\begin{aligned} \mu (R{\setminus } (A\cap F))\le \mu (R{\setminus } A) + \mu (R{\setminus } F) \le 3{\varepsilon }\,\mu (R). \end{aligned}$$

(3.3)

For a given cube $Q\in {\mathcal D}$, we denote $B_Q = \bar{B}(x_Q,3\mathrm{diam}(Q))$, where $x_Q$ stands for the center of Q. Given some big constant $M>N$, we consider now the following subfamilies of cubes from ${\mathcal D}(R)$:

• We say that $Q\in {\mathcal D}$ belongs to ${\mathsf {HD}}_0$ if $Q\subset 3R$, $\mathrm{diam}(Q)\le r_0/10$ and $\mu (B_Q)\ge M\,\ell (Q)^n$.

• We say that $Q\in {\mathcal D}$ belongs to ${\mathsf {LD}}_0$ if $Q\subset 3R$, $\mathrm{diam}(Q)\le r_0/10$ and $\mu (3Q)\le M^{-1}\,\ell (Q)^n$.

• We say that $Q\in {\mathcal D}$ belongs to ${\mathsf {BA}}_0$ if $Q\subset 3R$, $\mathrm{diam}(Q)\le r_0/10$, $Q\not \in {\mathsf {HD}}_0\cup {\mathsf {LD}}_0$, and $Q\cap F= \varnothing$.

We denote by $\mathrm{Stop}$ the family of maximal (and thus disjoint) cubes from ${\mathsf {HD}}_0\cup {\mathsf {LD}}_0\cup {\mathsf {BA}}_0$. We set ${\mathsf {HD}}=\mathrm{Stop}\cap {\mathsf {HD}}_0$, ${\mathsf {LD}}=\mathrm{Stop}\cap {\mathsf {LD}}_0$, and ${\mathsf {BA}}=\mathrm{Stop}\cap {\mathsf {BA}}_0$. The notations ${\mathsf {HD}}$, ${\mathsf {LD}}$, and ${\mathsf {BA}}$ stand for “high density”, “low density”, and “big alpha’s”, respectively.

Lemma 3.1

For M big enough, we have

$$\begin{aligned} R\cap \bigcup _{Q\in \mathrm{Stop}} Q \subset (R{\setminus } A)\cup (R{\setminus } F), \end{aligned}$$

and thus

$$\begin{aligned} \mu \biggl (R\cap \bigcup _{Q\in \mathrm{Stop}} Q \biggr )\le 3{\varepsilon }\,\mu (R). \end{aligned}$$

Proof

Since the second statement is an immediate consequence of the first one, we only have to show that if $Q\in {\mathcal D}(R)\cap \mathrm{Stop}$, then $Q\subset (R{\setminus } A)\cup (R{\setminus } F)$.

Suppose first that $Q\in {\mathsf {HD}}$. Since for any $x\in Q$ we have $B_{Q}\subset B(x,6\mathrm{diam}(Q))$, setting $r=6\,\mathrm{diam}(Q)$ we get

$$\begin{aligned} \mu (B(x,r)) \ge \mu (B_Q) \ge M\,\ell (Q)^n = c_7\,M\,r^n> 4N\,r^n, \end{aligned}$$

assuming $M> c_7^{-1}4N$. Since $r=\mathrm{diam}(6Q)\le 6r_0/10\le r_0$, it turns out that $x\not \in A$. Hence $Q\subset R{\setminus } A$.

Consider now a cube $Q\in {\mathsf {LD}}$. Notice that $B(x,\ell (Q))\subset 3Q$ for every $x\in Q$. Thus,

$$\begin{aligned} \mu \bigl (B(x,\ell (Q))\bigr )\le \mu (3Q)\le \frac{1}{M} \,\ell (Q)^n. \end{aligned}$$

Thus, $x\in R{\setminus } A$ because $M>N$. So $Q\subset R{\setminus } A$.

Finally, if $Q\in {\mathsf {BA}}$, then $Q\cap F=\varnothing$ and thus $Q\subset R{\setminus } F$. $\square$

We denote by $\mathcal G$ the subset of the cubes from ${\mathcal D}$ with $\mathrm{diam}(Q)\le r_0/10$ which are not contained in any cube from $\mathrm{Stop}$. We also set ${\mathcal G}(R) = {\mathcal G}\cap {\mathcal D}(R)$.

For a given cube $Q\in {\mathcal D}$, we denote

$$\begin{aligned} \alpha _\mu (Q) = \alpha _\mu (B_Q). \end{aligned}$$

(3.4)

Recall that $B_Q = \bar{B}(x_Q,3\mathrm{diam}(Q))$.

Lemma 3.2

For all $x\in 3R\cap \mathrm{supp}\mu$, we have

$$\begin{aligned} \sum _{Q\in {\mathcal G}:x\in Q} \alpha _\mu (Q)^2 \le c\,N. \end{aligned}$$

Proof

Let $Q\in {\mathcal G}$ and $z\in Q\cap \mathrm{supp}\mu$. Since $B_Q\subset \bar{B}(z,6\mathrm{diam}(Q))$, for any $r\in [6\,\mathrm{diam}(Q),12\,\mathrm{diam}(Q)]$ we have

$$\begin{aligned}\alpha _\mu (Q) \le c\,\alpha _\mu (z,r),\end{aligned}$$

and thus

$$\begin{aligned} \alpha _\mu (Q)^2\le c\int _{6\mathrm{diam}(Q)}^{12\mathrm{diam}(Q)}\alpha _\mu (z,r)^2\,\frac{dr}{r}. \end{aligned}$$

(3.5)

Given $x\in 3R\cap \mathrm{supp}\mu$, consider some cube $P\in {\mathcal G}$ such that $x\in P$. Since $P\not \in {\mathsf {BA}}$, there exists some $z\in F\cap P$, and then from 3.5 we derive

$$\begin{aligned} \sum _{Q\in {\mathcal G}:Q\supset P} \alpha _\mu (Q)^2&\le c\sum _{Q\in {\mathcal G}: Q\supset P} \int _{6\mathrm{diam}(P)}^{12\mathrm{diam}(P)}\alpha _\mu (z,r)^2\,\frac{dr}{r} \\&\le c \int _0^\infty \alpha _\mu (z,r)^2\,\frac{dr}{r}\le c\,N. \end{aligned}$$

Since this holds for all $P\in {\mathcal G}$ which contains x, the lemma follows. $\square$

3.3 A key estimate

Lemma 3.3

Let $Q\in {\mathcal G}(R)$. Let $L_Q$ be the line minimizing $\alpha (Q)$ and $x\in 3Q\cap \mathrm{supp}\mu$. If there exists some $S_x\in \mathrm{Stop}$ such that $x\in S_x$, then set $\ell _x=\ell (S_x)$. Otherwise, set $\ell _x=0$. We have

$$\begin{aligned}\mathrm{dist}(x,L_Q)\le c(M)\sum _{P\in {\mathcal G}:x\in P\subset 3Q}\alpha _\mu (P)\,\ell (P) + c\,\ell _x.\end{aligned}$$

We will not prove this result in detail because the arguments are almost the same as the ones in Lemma 5.2 of [18]. We just give a concise sketch.

Sketch of the proof

Let $x\in 3Q\cap \mathrm{supp}\mu$ and suppose that $\ell _x\ne 0$. For $i\ge 1$, denote by $Q_i$ the dyadic cube with side length $2^{-i}\ell (Q)$ that contains x, so that $Q_m$ is the parent of the cube $S_x$ in the lemma, and $Q_i\in {\mathcal G}(R)$ for $1\le i \le m$. Set also $Q_0=Q$. For $0\le i \le m$, let $L_{Q_i}$ be some n-plane minimizing $\alpha _\mu (Q_i)$ and denote by $\Pi _i$ the orthogonal projection onto $L_{Q_i}$.

Let $x_m=\Pi _m(x)$, and by backward induction set $x_{i-1}=\Pi _{i-1}(x_i)$ for $i=m,\ldots ,1$. Then we set

$$\begin{aligned} \mathrm{dist}(x,L_Q)\le |x_0-x|\le \sum _{i=1}^{m}|x_{i-1} - x_i| + |x_{m}-x|. \end{aligned}$$

(3.6)

It is clear that $|x_{m-1}-x|\lesssim \ell _x$, and one can check also that, for $1\le i \le m$,

$$\begin{aligned} |x_{i-1} - x_i|\lesssim \mathrm{dist}_H(L_{Q_{i-1}}\cap B_{Q_i}, \,L_{Q_i}\cap B_{Q_i}), \end{aligned}$$

(3.7)

where $\mathrm{dist}_H$ stands for the Hausdorff distance. Further, it turns out that

$$\begin{aligned} \mathrm{dist}_H(L_{Q_{i-1}}\cap B_{Q_i}, \,L_{Q_i}\cap B_{Q_i})\lesssim \alpha _\mu (Q_i)\,\ell (Q_i), \end{aligned}$$

(3.8)

with the implicit constant depending on M. This estimate has been proved in Lemma 3.4 of [18] in the case when $\mu$ is AD-regular. It is not difficult to check that the same arguments also work for the cubes $Q_i$, $1\le i \le m$, due to the fact that

$$\begin{aligned}M^{-1}\ell (Q_i)^n\le \mu (3Q_i)\le \mu (B_{Q_i})\le M\,\ell (Q_i)^n.\end{aligned}$$

From 3.6, 3.7 and 3.8, the lemma follows. $\square$

3.4 Proof of 3.2

Given a cube $Q \subset {\mathbb R}^d$, we set

$$\begin{aligned} \beta _{\mu ,2}(Q) = \inf _L \left( \frac{1}{\ell (Q)^n} \int _{3Q} \left( \frac{\mathrm{dist}(y,L)}{\ell (Q)}\right) ^2\,d\mu (y)\right) ^{1/2}, \end{aligned}$$

(3.9)

where the infimum is taken over all n-planes $L\subset {\mathbb R}^d$. Instead, we could also have set $\beta _{\mu ,2}(Q)=\beta _{\mu ,2}(B_Q)$, analogously to the definition of $\alpha _\mu (Q)$ in 3.4. However, for technical reasons, the definition in 3.9 is more appropriate.

To prove 3.2 we will show first the next result.

Lemma 3.4

The following holds:

$$\begin{aligned}\sum _{Q\in {\mathcal G}(R)} \beta _{\mu ,2}(Q)^2\,\mu (Q)\le C(M,N)\,\mu (3R).\end{aligned}$$

Proof

Consider a cube $Q\in {\mathcal G}(R)$. By Lemma 3.3, for all $x\in 3Q\cap \mathrm{supp}\mu$ we have

$$\begin{aligned} \mathrm{dist}(x,L_Q)\le c(M)\sum _{P\in {\mathcal G}:x\in P\subset 3Q}\alpha _\mu (P)\,\ell (P) + c\,\ell _x. \end{aligned}$$

So we get

$$\begin{aligned} \mathrm{dist}(x,L_Q)^2&\le c(M)\left( \sum _{P\in {\mathcal G}:x\in P\subset 3Q}\alpha _\mu (P)\,\ell (P)\right) ^2 + c\,\ell _x^2\\&\le c(M)\sum _{P\in {\mathcal G}:x\in P\subset 3Q}\alpha _\mu (P)^2\,\ell (P)\ell (Q) + c\,\ell _x^2. \end{aligned}$$

Then we have

$$\begin{aligned} \beta _{\mu ,2}(Q)^2&\lesssim _M&\frac{1}{\ell (Q)^{n+2}} \int _{3Q} \sum _{P\in {\mathcal G}:P\subset 3Q}\alpha _\mu (P)^2\,\ell (P)\ell (Q)\chi _P(x) \,d\mu (x)\\&+ \frac{1}{\ell (Q)^{n+2}} \int _{3Q} \sum _{P\in \mathrm{Stop}:P\subset 3Q} \ell (P)^2\chi _P(x) \,d\mu (x)\\= & {} \sum _{P\in {\mathcal G}:P\subset 3Q}\alpha _\mu (P)^2\,\frac{\mu (P)\ell (P)}{\ell (Q)^{n+1}} + \sum _{P\in \mathrm{Stop}:P\subset 3Q} \frac{\mu (P)\ell (P)^2}{\ell (Q)^{n+2}}. \end{aligned}$$

Thus we obtain

$$\begin{aligned} \sum _{Q\in {\mathcal G}(R)} \beta _2(Q)^2\,\mu (Q)&\lesssim _M \sum _{Q\in {\mathcal G}(R)}\sum _{P\in {\mathcal G}:P\subset 3Q}\alpha _\mu (P)^2\,\frac{\mu (P)\,\ell (P)\,\mu (Q)}{\ell (Q)^{n+1}}\nonumber \\&\quad +\sum _{Q\in {\mathcal G}(R)} \sum _{P\in \mathrm{Stop}:P\subset 3Q} \frac{\mu (P)\ell (P)^2\,\mu (Q)}{\ell (Q)^{n+2}} = : I+ II. \end{aligned}$$

(3.10)

First we deal with the term II. By Fubini, we have

$$\begin{aligned} II= \sum _{P\in \mathrm{Stop}}\mu (P)\,\ell (P)^2 \sum _{Q\in {\mathcal G}(R):3Q\supset P} \frac{\mu (Q)}{\ell (Q)^{n+2}}. \end{aligned}$$

Since $\mu (Q)\le M\,\ell (Q)^n$ for all $Q\in {\mathcal G}(R)$, the last sum above does not exceed $C(M)/\ell (P)^2$. Thus,

$$\begin{aligned} II\le C(M) \sum _{P\in \mathrm{Stop}}\mu (P)\le C(M)\,\mu (3R). \end{aligned}$$

Finally, we turn our attention to the term I in 3.10:

$$\begin{aligned}I= \sum _{P\in {\mathcal G}:P\subset 3R}\alpha _\mu (P)^2\,\mu (P)\,\ell (P) \sum _{Q\in {\mathcal G}(R):3Q\supset P} \frac{\mu (Q)}{\ell (Q)^{n+1}}. \end{aligned}$$

Using again that $\mu (Q)\le M\,\ell (Q)^n$ for all $Q\in {\mathcal G}(R)$, we derive

$$\begin{aligned}I \le c(M) \sum _{P\in {\mathcal G}:P\subset 3R}\alpha _\mu (P)^2\,\mu (P). \end{aligned}$$

By Lemma 3.2, the sum on the right hand side above does not exceed $C(N)\,\mu (3R)$, and so the lemma follows. $\square$

Now we can easily prove the estimate 3.2. Indeed, arguing as in Sect. 2.5, for some constant $c_8>0$ we get

$$\begin{aligned} \int _{A\cap F}\int _0^{c_8\,r_0} \beta _{\mu ,2}(x,r)^2\,\frac{dr}{r}\le c \sum _{Q\in {\mathcal G}(R)} \beta _{\mu ,2}(Q)^2\,\mu (Q)\le C(M,N)\,\mu (3R). \end{aligned}$$

Thus

$$\begin{aligned}\int _0^\infty \beta _{\mu ,2}(x,r)^2\,\frac{dr}{r}<\infty \quad \mathrm{for}\,\, \mu -\mathrm{a.e.}\,\, x\in A\cap F. \end{aligned}$$

Recalling that, by 3.3, $\mu (R{\setminus } (A\cap F)) \le 3{\varepsilon }\,\mu (R)$ and that ${\varepsilon }$ can be taken arbitrarily small, it turns out that

$$\begin{aligned} \int _0^\infty \beta _{\mu ,2}(x,r)^2\,\frac{dr}{r}<\infty \quad \mathrm{for }\,\, \mu -\mathrm{a.e.}\,\, x\in R. \end{aligned}$$

Since this holds for any dyadic cube R with $\mu (R)>0$, 3.2 is proved.