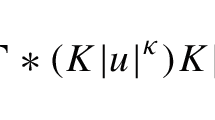Skip to main content
SpringerLink
Log in

Semi-classical states for the Choquard equation

  • Published:
Calculus of Variations and Partial Differential Equations Aims and scope Submit manuscript

Abstract

We study the nonlocal equation

$$\begin{aligned} -\varepsilon ^2 \Delta u_\varepsilon +V u_\varepsilon = \varepsilon ^{-\alpha }\bigl (I_\alpha *|u_\varepsilon |^p\bigr ) |u_\varepsilon |^{p - 2} u_\varepsilon \quad \text {in }{\mathbb {R}}^N, \end{aligned}$$

where \(N \ge 1\), \(\alpha \in (0, N)\), \(I_\alpha (x) = A_\alpha /|x |^{N - \alpha }\) is the Riesz potential and \(\varepsilon > 0\) is a small parameter. We show that if the external potential \(V \in C ({\mathbb {R}}^N; [0, \infty ))\) has a local minimum and \(p \in [2, (N + \alpha )/(N - 2)_+)\) then for all small \(\varepsilon > 0\) the problem has a family of solutions concentrating to the local minimum of \(V\) provided that: either \(p>1 + \max (\alpha , \frac{\alpha + 2}{2})/(N - 2)_+\), or \(p > 2\) and \(\liminf _{|x | \rightarrow \infty } V (x) |x |^2 > 0\), or \(p = 2\) and \(\inf _{x \in {\mathbb {R}}^N} V (x) (1 + |x |^{N-\alpha })>0\). Our assumptions on the decay of \(V\) and admissible range of \(p\ge 2\) are optimal. The proof uses variational methods and a novel nonlocal penalization technique that we develop in this work.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. It should be noted that lemma 15 in [50] only holds when there exists \(\gamma < 1\) such that \(\liminf _{|x | \rightarrow \infty } V (x) |x |^\gamma > 0\) (in the first term in (10) therein, one should read \(v(y)\) instead of \(v (x)\)). It is known that if \(\limsup _{|x | \rightarrow \infty } V (x) |x |^\gamma = 0\) for some \(\gamma > 1\), the problem (1) considered in [50] does not have a positive solution [41, theorem 3].

References

  1. Adams, R.A.: Sobolev Spaces. Pure and Applied Mathematics, vol. 65. Academic Press, New York (1975)

  2. Agmon, S.: On positivity and decay of solutions of second order elliptic equations on Riemannian manifolds. In: Methods of Functional Analysis and Theory of Elliptic Equations (Naples, 1982), Liguori, Naples, pp. 19–52 (1983)

  3. Ambrosetti, A., Badiale, M., Cingolani, S.: Semiclassical states of nonlinear Schrödinger equations. Arch. Ration. Mech. Anal. 140(3), 285–300 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  4. Ambrosetti, A., Felli, V., Malchiodi, A.: Ground states of nonlinear Schrödinger equations with potentials vanishing at infinity. J. Eur. Math. Soc. 7(1), 117–144 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  5. Ambrosetti, A., Malchiodi, A.: Perturbation Methods and Semilinear Elliptic Problems on R\(^{n}\). Progress in Mathematics, vol. 240. Birkhäuser Verlag, Basel (2006)

  6. Ambrosetti, A., Malchiodi, A.: Concentration phenomena for nonlinear Schrödinger equations: recent results and new perspectives. In: Berestycki, H., Bertsch, M., Browder, F.E., Nirenberg, L., Peletier, L.A., Véron, L. (eds.) Perspectives in Nonlinear Partial Differential Equations. Contemporary Mathematics, vol. 446, pp. 19–30. American Mathematical Society, Providence (2007)

  7. Ambrosetti, A., Prodi, G.: A Primer of Nonlinear Analysis. Cambridge Studies in Advanced Mathematics, vol. 34. Cambridge University Press, Cambridge (1993)

  8. Ambrosetti, A., Rabinowitz, P.H.: Dual variational methods in critical point theory and applications. J. Funct. Anal. 14, 349–381 (1973)

    Article  MATH  MathSciNet  Google Scholar 

  9. Appell, J., Zabrejko, P.P.: Nonlinear Superposition Operators. Cambridge Tracts in Mathematics, vol. 95. Cambridge University Press, Cambridge (1990)

  10. Bonheure, D., Di Cosmo, J., Van Schaftingen, J.: Nonlinear Schrödinger equation with unbounded or vanishing potentials: solutions concentrating on lower dimensional spheres. J. Differ. Equ. 252(2), 941–968 (2012)

    Article  MATH  Google Scholar 

  11. Bonheure, D., Van Schaftingen, J.: Nonlinear Schrödinger equations with potentials vanishing at infinity. C. R. Math. Acad. Sci. Paris 342(12), 903–908 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  12. Bonheure, D., Van Schaftingen, J.: Bound state solutions for a class of nonlinear Schrödinger equations. Rev. Mat. Iberoam. 24(1), 297–351 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  13. Bonheure, D., Van Schaftingen, J.: Groundstates for the nonlinear Schrödinger equation with potential vanishing at infinity. Ann. Mat. Pura Appl. (4) 189(2), 273–301 (2010)

    Google Scholar 

  14. Byeon, J., Wang, Z.-Q.: Standing waves with a critical frequency for nonlinear Schrödinger equations. Arch. Ration. Mech. Anal. 165(4), 295–316 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  15. Byeon, J., Wang, Z.-Q.: Standing waves with a critical frequency for nonlinear Schrödinger equations. II. Calc. Var. Partial Differ. Equ. 18(2), 207–219 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  16. Cingolani, S., Clapp, M., Secchi, S.: Multiple solutions to a magnetic nonlinear Choquard equation. Z. Angew. Math. Phys. 63(2), 233–248 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  17. Cingolani, S., Jeanjean, L., Secchi, S.: Multi-peak solutions for magnetic NLS equations without non-degeneracy conditions. ESAIM Control Optim. Calc. Var. 15(3), 653–675 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  18. Cingolani, S., Secchi, S.: Multiple S\(^{1}\)-orbits for the Schrödinger-Newton system. Differ. Integral Equ. 26(9/10), 867–884 (2013)

    MATH  MathSciNet  Google Scholar 

  19. Cingolani, S., Secchi, S., Squassina, M.: Semi-classical limit for Schrödinger equations with magnetic field and Hartree-type nonlinearities. Proc. R. Soc. Edinb. Sect. A 140(5), 973–1009 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  20. Clapp, M., Salazar, D.: Positive and sign changing solutions to a nonlinear Choquard equation. J. Math. Anal. Appl. 407(1), 1–15 (2013)

    Article  MathSciNet  Google Scholar 

  21. del Pino, M., Felmer, P.L.: Semi-classical states for nonlinear Schrödinger equations. J. Funct. Anal. 149(1), 245–265 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  22. del Pino, M., Felmer, P.L.: Multi-peak bound states for nonlinear Schrödinger equations. Ann. Inst. H. Poincaré Anal. Non Linéaire 15(2), 127–149 (1998)

    Google Scholar 

  23. Di Cosmo, J., Van Schaftingen, J.: Stationary solutions of the nonlinear Schrödinger equation with fast-decay potentials concentrating around local maxima. Calc. Var. Partial Differ. Equ. 47(1–2), 243–271 (2013)

    Article  MATH  Google Scholar 

  24. Floer, A., Weinstein, A.: Nonspreading wave packets for the cubic Schrödinger equation with a bounded potential. J. Funct. Anal. 69(3), 397–408 (1986)

    Article  MATH  MathSciNet  Google Scholar 

  25. Genev, H., Venkov, G.: Soliton and blow-up solutions to the time-dependent Schrödinger–Hartree equation. Discrete Contin. Dyn. Syst. Ser. S 5(5), 903–923 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  26. Herbst, I.W.: Spectral theory of the operator (\(p^{2}+m^{2})^{1/2}-Ze^{2}/r\). Commun. Math. Phys. 53(3), 285–294 (1977)

    Article  MATH  MathSciNet  Google Scholar 

  27. Jones, K.R.W.: Gravitational self-energy as the litmus of reality. Mod. Phys. Lett. A 10(8), 657–668 (1995)

    Article  Google Scholar 

  28. Jones, K.R.W.: Newtonian quantum gravity. Aust. J. Phys. 48(6), 1055–1081 (1995)

    Article  Google Scholar 

  29. Kwon, O.: Existence of standing waves of nonlinear Schrödinger equations with potentials vanishing at infinity. J. Math. Anal. Appl. 387(2), 920–930 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  30. Lieb, E.H.: Existence and uniqueness of the minimizing solution of Choquard’s nonlinear equation. Stud. Appl. Math. 57(2), 93–105 (1976/1977)

    Google Scholar 

  31. Lieb, E.H., Loss, M.: Analysis, 2nd edn. Graduate Studies in Mathematics, vol. 14. American Mathematical Society, Providence (2001)

  32. Lions, P.-L.: The Choquard equation and related questions. Nonlinear Anal. 4(6), 1063–1072 (1980)

    Article  MATH  MathSciNet  Google Scholar 

  33. Lions, P.-L.: The concentration-compactness principle in the calculus of variations. The locally compact case. I. Ann. Inst. H. Poincaré Anal. Non Linéaire 1(2), 109–145 (1984)

    Google Scholar 

  34. Ma, L., Zhao, L.: Classification of positive solitary solutions of the nonlinear Choquard equation. Arch. Ration. Mech. Anal. 195(2), 455–467 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  35. Menzala, G.P.: On regular solutions of a nonlinear equation of Choquard’s type. Proc. R. Soc. Edinb. Sect. A 86(3–4), 291–301 (1980)

    Article  MATH  MathSciNet  Google Scholar 

  36. Menzala, G.P.: On the nonexistence of solutions for an elliptic problem in unbounded domains. Funkc. Ekvacio 26(3), 231–235 (1983)

    MATH  MathSciNet  Google Scholar 

  37. Moroz, I.M., Penrose, R., Tod, P.: Spherically-symmetric solutions of the Schrödinger–Newton equations. Class. Quantum Gravity 15(9), 2733–2742 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  38. Moroz, V., Van Schaftingen, J.: Existence and concentration for nonlinear Schrödinger equations with fast decaying potentials. C. R. Math. Acad. Sci. Paris 347(15–16), 921–926 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  39. Moroz, V., Van Schaftingen, J.: Semiclassical stationary states for nonlinear Schrödinger equations with fast decaying potentials. Calc. Var. Partial Differ. Equ. 37(1–2), 1–27 (2010)

    Article  MATH  Google Scholar 

  40. Moroz, V., Van Schaftingen, J.: Nonlocal Hardy type inequalities with optimal constants and remainder terms. Ann. Univ. Buchar. Math. Ser. 3(LXI)(2), 187–200 (2012)

    Google Scholar 

  41. Moroz, V., Van Schaftingen, J.: Nonexistence and optimal decay of supersolutions to Choquard equations in exterior domains. J. Differ. Equ. 254(8), 3089–3145 (2013)

    Article  MATH  Google Scholar 

  42. Moroz, V., Van Schaftingen, J.: Groundstates of nonlinear Choquard equations: existence, qualitative properties and decay asymptotics. J. Funct. Anal. 265(2), 153–184 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  43. Moroz, V., Van Schaftingen, J.: Existence of groundstates for a class of nonlinear Choquard equations. Trans. Am. Math. Soc. arXiv:1212.2027

  44. Pekar, S.: Untersuchung über die Elektronentheorie der Kristalle. Akademie Verlag, Berlin (1954)

    Google Scholar 

  45. Penrose, R.: On gravity’s role in quantum state reduction. Gen. Relativ. Gravitat. 28(5), 581–600 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  46. Pinchover, Y., Tintarev, K.: A ground state alternative for singular Schrödinger operators. J. Funct. Anal. 230(1), 65–77 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  47. Rabinowitz, P.H.: Minimax methods in critical point theory with applications to differential equations. In: CBMS Regional Conference Series in Mathematics, vol. 65, Published for the Conference Board of the Mathematical Sciences, Washington, DC (1986)

  48. Riesz, M.: L’intégrale de Riemann-Liouville et le problème de Cauchy. Acta Math. 81, 1–223 (1949)

    Article  MATH  MathSciNet  Google Scholar 

  49. Schwartz, J.T.: Nonlinear Functional Analysis. Gordon and Breach, New York (1969)

    MATH  Google Scholar 

  50. Secchi, S.: A note on Schrödinger–Newton systems with decaying electric potential. Nonlinear Anal. 72(9–10), 3842–3856 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  51. Stein, E.M., Weiss, G.: Fractional integrals on n-dimensional Euclidean space. J. Math. Mech. 7, 503–514 (1958)

    MATH  MathSciNet  Google Scholar 

  52. Struwe, M.: Variational methods: applications to nonlinear partial differential equations and Hamiltonian systems, 4th edn. In: Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge, vol. 34. Springer, Berlin (2008)

  53. Tod, P., Moroz, I.M.: An analytical approach to the Schrödinger–Newton equations. Nonlinearity 12(2), 201–216 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  54. Wei, J., Winter, M.: Strongly interacting bumps for the Schrödinger–Newton equations. J. Math. Phys. 50(1), 012905, 22 (2009)

    Google Scholar 

  55. Willem, M.: Minimax Theorems. Progress in Nonlinear Differential Equations and their Applications, vol. 24. Birkhäuser, Boston (1996)

  56. Willem, M.: Functional Analysis: Fundamentals and Applications. Cornerstones, vol. XIV. Birkhäuser, Basel (2013)

  57. Yin, H., Zhang, P.: Bound states of nonlinear Schrödinger equations with potentials tending to zero at infinity. J. Differ. Equ. 247(2), 618–647 (2009)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Swansea University, Singleton Park, Swansea, SA2 8PP, Wales, UK

    Vitaly Moroz

  2. Institut de Recherche en Mathématique et Physique, Université Catholique de Louvain, Chemin du Cyclotron 2 bte L7.01.01, 1348 , Louvain-la-Neuve, Belgium

    Jean Van Schaftingen

Authors
  1. Vitaly Moroz
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jean Van Schaftingen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jean Van Schaftingen.

Additional information

Communicated by P. Rabinowitz.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Moroz, V., Van Schaftingen, J. Semi-classical states for the Choquard equation. Calc. Var. 52, 199–235 (2015). https://doi.org/10.1007/s00526-014-0709-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00526-014-0709-x

Mathematics Subject Classification (1991)

Search

Navigation