Skip to main content
SpringerLink
Log in

On certain hyperelliptic signals that are natural controls for nonholonomic motion planning

  • Original Article
  • Published:
Mathematics of Control, Signals, and Systems Aims and scope Submit manuscript

Abstract

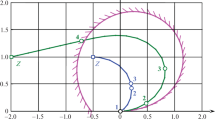
In this paper, we address the general problem of approximating, in a certain optimal way, non-admissible motions of a kinematic system with nonholonomic constraints. Since this kind of problems falls into the general subriemannian geometric setting, it is natural to consider optimality in the sense of approximating by means of subriemannian geodesics. We consider systems modeled by a subriemannian Goursat structure, a particular case being the well-known system of a car with trailers, along with the associated parallel parking problem. Several authors approximate the successive Lie brackets using trigonometric functions. By contrast, we show that more natural optimal motions are related with closed hyperelliptic plane curves with a certain number of loops.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Sussmann HJ, Laferriere G (1991) Motion planning for controllable systems without drift. In: Proceedings of the IEEE conference on robotics and automation, Sacramento, CA, April 1991. IEEE Publications, New York, pp 109–148

  2. Sussmann HJ, Liu WS (1993) Lie bracket extensions and averaging: the single bracket generating case. In: Li ZX, Canny JF (eds) Non-holonomic motion planning. Kluwer Academic Publishers, Boston, pp 109–148

  3. Tilbury D, Murray RM, Sastry S (1995) Trajectory generation for the n-trailer problem using Goursat normal form. IEEE Trans Automat Contr 40(5):802–819

    Article  MathSciNet  MATH  Google Scholar 

  4. Tilbury D, Laumond J, Murray R, Sastry S, Walsh G (1992) Steering car-like systems with trailers using sinusoids. In: Proceedings of the IEEE international conference on robotics and automation (ICRA) pp 1993–1998

  5. Jean F (2001) Complexity of nonholonomic motion planning. Int J Control 74(8):776–782

    Article  MathSciNet  MATH  Google Scholar 

  6. Jean F (2003) Entropy and complexity of a path in subriemannian geometry. COCV 9:485–506

    Article  MathSciNet  MATH  Google Scholar 

  7. Jean F, Falbel E (2003) Measures and transverse paths in subriemannian geometry. J Anal Math 91:231–246

    Article  MathSciNet  MATH  Google Scholar 

  8. Boizot N, Gauthier JP (2013) Motion planning for kinematic systems. IEEE TAC 58(6):1430–1442

    MathSciNet  Google Scholar 

  9. Boizot N, Gauthier JP (2013) On the motion planning of the ball with a trailer. Math Control Relat Fields 3(3):269–286

    Article  MathSciNet  MATH  Google Scholar 

  10. Gauthier JP, Zakalyukin V (2006) On the motion planning problem, complexity, entropy and nonholonomic interpolation. J Dyn Control Syst 12(3):371–404

    Article  MathSciNet  MATH  Google Scholar 

  11. Gauthier JP, Jakubczyk B, Zakalyukin V (2010) Motion planning and fastly oscillating controls. SIAM J Control Optic 48(5):3433–3448

    Article  MathSciNet  MATH  Google Scholar 

  12. Romero-melendez C, Gauthier JP, Monroy-Perez F (2004) On complexity and motion planning for corank one sub-riemannian metrics. COCV 10:634–655

    Article  MathSciNet  MATH  Google Scholar 

  13. Gauthier JP, Zakalyukin V (2005) On the codimension one motion planning problem. J Dyn Control Syst 11(1):73–89

    Article  MathSciNet  MATH  Google Scholar 

  14. Gauthier JP, Zakalyukin V (2005) On the one-step-bracket-generating motion planning problem. J Dyn Control Syst 11(2):215–235

    Article  MathSciNet  MATH  Google Scholar 

  15. Laumond JP, Sekhavat S, Lamiraux F (1998) Guidelines in nonholonomic motion planning for mobile robots. In: Robot motion planning and control, Springer, Berlin

  16. Morin P, Samson C (2003) Practical stabilization of driftless systems on lie groups: the transverse function approach. IEEE Trans Automat Control 48:1496–1508

    Article  MathSciNet  Google Scholar 

  17. Fliess M, Levine J, Martin P, Rouchon P (1995) Flatness and defect of non-linear systems: introductory theory and examples. Int J Control 61:1327–1361

    Article  MathSciNet  MATH  Google Scholar 

  18. Montgomery R, Zhitomirskii MY (2001) Geometric approach to Goursat flags. Ann Inst H Poincaré, Anal Non Linéaire 18:459–493

    Article  MathSciNet  MATH  Google Scholar 

  19. Love AEH (1944) A treatise on the mathematical theory of elasticity. Dover, New York

    MATH  Google Scholar 

  20. Anzaldo-Meneses A, Monroy-Perez F (2003) Goursat distributions and subriemannian structures. J Math Phys 44(12):6101–6111

    Article  MathSciNet  MATH  Google Scholar 

  21. Gauthier JP, Kawski M (2014) Minimal complexity sinusoidal controls for path planning. In: Proceedings of the 53th IEEE, CDC conference, pp 3731–3736

  22. Bellaiche A (1997) The tangent space in sub-Riemannian geometry. J Math Sci 83(4):461–476

    Article  MathSciNet  MATH  Google Scholar 

  23. Bianchini RM, Stefani G (1990) Graded approximations and controllability along a trajectory. SIAM J Control Optim 28:903–924

    Article  MathSciNet  MATH  Google Scholar 

  24. Bressan A (1985) Local asymptotic approximation of non linear control systems. Int J Control 41:1331–1336

    Article  MathSciNet  MATH  Google Scholar 

  25. von Weber E (1898) Zur Invariantentheorie der Systeme Pfaff’scher Gleichungen. Berichte über die Verhandlungen der Königlich Sächsischen Gesellshaft der Wissenshaften. Math Phys Klasse Leipzig 50:207–229

    Google Scholar 

  26. Teel AR, Murray RM, Walsh G (1992) Non-holonomic control systems: from steering to stabilization with sinusoids, IEEE conference on decision and control, pp 1603–1609

  27. Agrachev AA, Sachkov YuL (2004) A control theory from the geometric viewpoint. Springer, Berlin

    Book  Google Scholar 

Download references

Acknowledgments

This paper was prepared during the sabbatical leave of the second author at the Laboratoire des Sciences de l’Information et des Systèmes (LSIS, UMR 7296) in the Université du Sud Toulon-Var, France. The author was financially supported by the CONACYT under the program of sabbatical leaves abroad for the reinforcement of the research groups, project number 204051.

Conflict of interest

Herewith I confirm, on behalf of all authors, that the information provided is accurate, and that we have no potential conflicts of interest.

Author information

Authors and Affiliations

  1. LSIS, UMR CNRS 7296 and Equipe INRIA GECO, Université de Toulon, UTLN, 83957, La Garde Cedex, France

    Jean-Paul Gauthier

  2. Departamento de Ciencias Básicas, Universidad Autónoma Metropolitana-Azcapotzalco, 02200, México D.F., México

    Felipe Monroy-Pérez

Authors
  1. Jean-Paul Gauthier
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Felipe Monroy-Pérez
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Felipe Monroy-Pérez.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gauthier, JP., Monroy-Pérez, F. On certain hyperelliptic signals that are natural controls for nonholonomic motion planning. Math. Control Signals Syst. 27, 415–437 (2015). https://doi.org/10.1007/s00498-015-0145-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00498-015-0145-2

Keywords

Search

Navigation