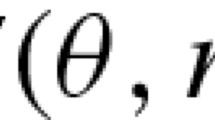Abstract
We consider the problem of stability in a class of differential equations which are driven by a differential measure associated with inputs of locally bounded variation. After discussing some existing notions of solution for such systems, we derive Lyapunov-based conditions on the system’s vector fields for asymptotic stability under a specific class of inputs. These conditions are based on the stability margin of the Lebesgue-integrable and the measure-driven components of the system. For more general inputs which do not necessarily lead to asymptotic stability, we then derive conditions such that the maximum norm of the resulting trajectory is bounded by some function of the total variation of the input, which generalizes the notion of integral input-to-state stability in measure-driven systems.
Similar content being viewed by others
Notes
It must be noted that for a measure d\(u\), the supremum norm cannot be defined and that is why the problem of ISS using essential supremum norm is not of interest for system (2) (also see Sect. 1.3.1 for an example). One may choose to call the proposed notion of stability as integral-ISS with respect to d\(u\), but in standard text books on functional analysis, integral norm of a measure d\(u\) is more commonly represented by the total variation of \(u(\cdot )\). Hence, we choose to work with the more standard terminology of total variation, while keeping in mind that conceptually it represents the integral norm of the input driving the system dynamics.
The sequence \(\{w_k\}_{k=1}^\infty \) converges to \(w^*\) in the distributional sense only, which means that
$$\begin{aligned} \lim _{k\rightarrow \infty } \int _{0}^{\infty }\phi (s) w_k(s) \mathrm{d}s = \int _{0}^{\infty }\phi (s) w^*(s) \mathrm{d}s \end{aligned}$$for every continuous function \(\phi (\cdot )\) supported over a compact domain. This notion of convergence is also called \(\text {weak}^*\)-convergence.
The choice of the interval \([0,1]\) is arbitrary and could be replaced by any other compact interval without changing the development much.
A function \(h:\mathbb {R}\rightarrow \mathbb {R}\) is called eventually non-increasing if there exists \(T\) such that for every \(\varepsilon _2 > \varepsilon _1 \ge 0\), it holds that \(h(T+\varepsilon _2) \le h(T+\varepsilon _1)\). Similarly, \(h(\cdot )\) is called eventually non-decreasing if \(-h(\cdot )\) is eventually non-increasing.
References
Acary V, Brogliato B, Goeleven D (2008) Higher order Moreau’s sweeping process: mathematical formulation and numerical simulation. Math Program Ser A 113:133–217
Ambrosio L, Fusco N, Pallara D (2000) Functions of bounded variation and free discontinuity problems. Clarendon Press, Oxford
Angeli D, Sontag E, Wang Y (2000) A characterization of integral input-to-state stability. IEEE Trans Autom Control 45(6):1082–1097
Bressan A (1987) On differential systems with impulsive controls. Rend Semin Mate Univ Padova 78:227–235
Bressan A, Rampazzo F (1993) On differential systems with quadratic impulses and their applications to Lagrangian mechanics. SIAM J Control Optim 31(5):1205–1220
Bressan A Jr, Rampazzo F (1991) Impulsive control systems with commutative vector fields. J Optim Theory Appl 71(1):67–83
Bressan A Jr, Rampazzo F (1994) Impulsive control systems without commutativity assumptions. J Optim Theory Appl 81(3):435–457
Brogliato B (2009) Some results on optimal control with unilateral constraints. Nonlinear Anal Theory Methods Appl 70:3626–3657
Carter TE (1991) Optimal impulsive space trajectories based on linear equations. J Optim Theory Appl 70(2):277–297
Claeys M, Arzelier D, Henrion D, Lasserre J-B (2012) Measures and LMI for impulsive optimal control with applications to space rendezvous problems. In: Proceedings of the American control conference, Montreal, pp 161–166
Code WJ, Silva GN (2010) Closed loop stability of measure-driven impulsive control systems. J Dyn Control Syst 16(1):1–21
Dal Maso G, Rampazzo F (1991) On systems of ordinary differential equations with measures as controls. J Differ Integral Equ 4(4):739–765
Das PC, Sharma RR (1972) Existence and stability of measure differential equations. Czechoslov Math J 22(1):145–158
Dashkovskiy S, Mironchenko A (2013) Input-to-state stability of nonlinear impulsive systems. SIAM J Control Optim 51(3):1962–1987
Dykhta VA (1999) Impulsive optimal control in models of economics and quantum electronics (in Russian). Avtom Telemekhanika 11:100–112
Feichtinger G, Hartl RF, Sethi SP (1994) Dynamic optimal control models in advertising: recent developments. J Manag Sci 40(2):195–226
Haddad WM, Chellaboina VS, Nersesov SG (2006) Princeton series in applied mathematics. Impulsive and hybrid dynamical systems. Princeton University Press, Princeton
Hájek O (1985) Book review: Differential systems involving impulses. Bull Am Math Soc 12:272–279
Hespanha JP, Liberzon D, Teel A (2008) Lyapunov conditions for input-to-state stability of impulsive systems. Automatica 44:2735–2744
Khalil HK (2002) Nonlinear systems, 3rd edn. Prentice-Hall Inc, London
Kurzweil J (1958) Generalized ordinary differential equations. Czechoslov Math J 8(3):360–388
Lakshmikantham V, Bainov DD, Simeonov PS (1989) Theory of impulsive differential equations. In: Series in modern applied mathematics, vol 6. World Scientific, Singapore
Lakshmikantham V, Liu X (1989) Stability criteria for impulsive differential equations in terms of two measures. J Math Anal Appl 137:591–604
Leela S (1974) Stability of measure differential equations. Pac J Math 55(2):489–498
Liu J, Liu X, Xie W-C (2011) Input-to-state stability of impulsive and switching hybrid systems with time-delay. Automatica 47(5):899–908
Miller BM (1996) The generalized solutions of nonlinear optimization problems with impulse control. SIAM J Control Optim 34(4):1420–1440
Monteiro Marques MDP (1993) Differential inclusions in nonsmooth mechanical problems: shocks and dry friction. In: Progress in nonlinear differential equations and their applications, vol 9. Birkhäuser, Basel
Moreau JJ (1988) Bounded variation in time. In: Moreau JJ, Panagiotopoulos PD, Strang G (eds) Topics in nonsmooth mechanics. Birkhäuser Verlag, Basel
Moreau JJ, Valadier M (1987) A chain rule involving vector functions of bounded variation. J Funct Anal 74(2):333–345
Munoz de la Pena D, Christofides PD (2007) Stability of nonlinear asynchronous systems. In: Proceedings of the 46th IEEE conference decision and control, New Orleans, pp 4576–4583
Neustadt LW (1965) A general theory of minimum-fuel space trajectories. SIAM J Control Ser A 3(2):317–356
Orlov Y (2002) Schwartz’ distributions in nonlinear setting: applications to differential equations, filtering and optimal control. Math Probl Eng 8(4–5):367–387
Pandit SG, Deo SG (1982) Differential systems involving impulses. In: Lecture notes in mathematics, vol 954. Springer-Verlag, New York
Rishel RW (1965) An extended Pontryagin principle for control systems whose control laws contain measures. SIAM J Control Ser A 3(2):191–205
Schaub H, Alfriend KT (2001) Impulsive feedback control to establish specific mean orbit elements of spacecraft formations. J Guid Navig Control 24(4):739–745
Schmaedeke WW (1965) Optimal control theory for nonlinear vector differential equations containing measures. SIAM J Control 3(2):231–280
Silva GN, Vinter RB (1997) Necessary conditions for optimal impulsive control problems. SIAM J Control Optim 35(6):1829–1846
Sontag ED (1989) Smooth stabilization implies coprime factorization. IEEE Trans Autom Control AC–34(4):435–443
Sontag ED (1998) Comments on integral variants of ISS. Syst Control Lett 34:93–100
Sontag ED (1998) Mathematical control theory: deterministic finite dimensional systems, 2nd edn. In: Textbooks in applied mathematics. Springer, New York
Sussmann HJ (1978) On the gap between deterministic and stochastic ordinary differential equations. Ann Probab 6(1):19–41
Tanwani A, Brogliato B, Prieur C (2014) Stability and observer design for multivalued Lur’e systems with nonmonotone, time-varying nonlinearities and state jumps. SIAM J Control Optim 52(6):3639–3672
Tanwani A, Trenn S (2013) An observer for switched differential-algebraic equations based on geometric characterization of observability. In: Proceedings of the 52nd IEEE conference decision and control, Florence, pp 5981–5986
Trenn S (2009) Regularity of distributional differential algebraic equations. Math Control Signals Syst 21(3):229–264
van de Wouw N, Leine RI (2012) Robust impulsive control of motion systems with uncertain friction. Int J Robust Nonlinear Control 22(4):369–397
Warga J (1966) Extended problems with unbounded controls. SIAM J Control Ser A 3(3):424–438
Xiaoa Y, Chen D, Qin H (2006) Optimal impulsive control in periodic ecosystem. Syst Control Lett 55(7):558–565
Zhang X, Shuai Z, Wang K (2004) Optimal impulsive harvesting policy for single population. Nonlinear Anal Real World Appl 4(4):639–651
Acknowledgments
We thank an anonymous reviewer for his suggestion on further generalizing the system class addressed in the earlier version of this paper, and the associate editor for suggesting us to give detailed arguments on dealing with accumulation points in the proof of Theorem 1.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Solution of MDEs
We study the existence of solution of system (5) and the content of this Appendix is primarily borrowed from [12]. Before arriving at the main result, we first recall a definition that is essential for the development to follow.
Definition 4
Let \(u:[t_0,T] \rightarrow R^m\) be an \(RCBV\) function and set
The canonical graph completion \(\varphi :[0,1] \rightarrow [t_0,T]\times \mathbb {R}^m\) of \(u(\cdot )\) is defined as:
As an illustration, we have sketched the function \(\varphi (s)\) in Fig. 1 corresponding to a piecewise-constant input \(u(\cdot )\) over a compact interval.
We now define a coordinate transformation using the canonical graph completion of the input. Let \(\varphi := (\varphi _0, \varphi _1, \dots , \varphi _m)\) denote the graph completion of \(u(\cdot )\) and consider the following auxiliary \((n+1)\)-dimensional Cauchy problem
where \(\tilde{y}:=(y_0,y): [0,1] \rightarrow [t_0,T] \times \mathbb {R}^n\). Since the graph completions (by definition) are Lipschitz continuous functions, the solutions of (38) are studied in the classical sense. The following result establishes the link between the solutions of auxiliary system (38) and (6).
Theorem 3
([12, Theorem 2.2]) Let \(u:[t_0,T] \rightarrow \mathbb {R}^m\) be an RCBV function. An RCBV function \(x(\cdot )\) is called a solution of (6) if and only if there exists a solution \(\tilde{y} = (y_0,y)\) of (38) corresponding to the canonical graph completion \(\varphi (\cdot )\) such that
for almost every \(t \in (t_0,T)\).
A straightforward consequence of this result is that there exists a unique solution to system (5) whenever there exists a unique solution to system (38) in the classical sense. Thus, if \(f(\cdot )\), \(g(\cdot )\) are continuously differentiable, then there exists a maximal interval over which the solution of (38), and hence (5), is well defined. This interval may include accumulation of the discontinuity points of \(u(\cdot )\) because the graph completions of discontinuous inputs are Lipschitz continuous and the solution of (38) is still well defined in that case. However, it is important to note that the forward completeness of the vector fields \(f(\cdot )\) and \(g(\cdot )\) is not sufficient to guarantee that the solution of (38b) is forward complete. While working with singularly continuous and scalar inputs, a counterexample has been given in [41, Section8]. In the same paper in Theorem 2, sufficient conditions were presented (which roughly state that \(f(\cdot )\) satisfies a linear growth condition and \(g(\cdot ) \in \mathcal {C}^1(\mathbb {R}^n, \mathbb {R}^n)\) with \(\frac{\partial g}{\partial x}\) uniformly bounded) which guarantee the existence and uniqueness of the solutions to (38) with \(u(\cdot )\) being continuous. Later, it was shown in [5, Theorem 2.1] that these conditions are sufficient for existence of global (in time) solutions of (38b). Without imposing such strong conditions on system vector fields, it is nonetheless assumed in this paper that there exists a unique solution to system (38) for every Lipschitz continuous function \(\varphi (\cdot )\).
Appendix B: Generalized comparison lemma
Lemma 1
(Comparison lemma for MDEs) Consider a continuous locally BV function \(u:[t_0,T] \rightarrow \mathbb {R}^m\) with \(du\) as the associated differential measure and another continuous locally BV function \(V:[t_0,T] \rightarrow \mathbb {R}\) that satisfies
Then for each \(t \in [t_0,T]\)
where \(\mu \) is the Lebesgue–Stieltjes measure associated with \(u(\cdot )\).
Proof
We split the proof in two steps:
Step 1: Consider a continuous BV function \(W:[t_0,T]\rightarrow \mathbb {R}\) such that
with \(W(t_0) = V(t_0)\). Let us consider a sequence \(\{u^k\}_{k=1}^\infty \) of continuously differentiable functions converging pointwise to \(u(\cdot )\) and having the property that
Let \(W^k(\cdot )\) represent the solution of (40) obtained by replacing \(\mathrm{d}u_j\) with \(\dot{u}_j^k \mathrm{d}t\), \(j = 1,\dots ,m\). Then
where \(\Psi (t,s) = \mathrm{e}^{-a(t-s)+b\sum _{j=1}^m (u_j^k(t)-u_j^k(s))}\) and \(W^k(t_0) = W(t_0)\) for each \(k \ge 1\). Using the inequalities \(\mathrm{e}^{-a(t-s)} \le 1\) and \(|u^k(t)-u^k(s)|_1 \le \int _{t_0}^t|\dot{u}^k(\tau )|_1 \mathrm{d}\tau \) for each \(s \in [t_0,t]\), \(t < t_1\), we obtain
Noting that, \({\Vert \dot{u}^k_{(t_0,t)}\Vert _1}\) denotes the total variation of \(\dot{u}_k(\cdot )\) over the interval \((t_0,t)\), so by construction \({\Vert \dot{u}^k_{(t_0,t)}\Vert _1}\) converges to \(|\mu |_{(t_0,t)}\). Hence,
Step 2: We now show that \(V(t) \le W(t)\) for each \(t \in [t_0,T]\), from which the desired result follows. Indeed, if \(V\) and \(W\) satisfy (39) and (40), then \(\overline{W}:= V-W\) satisfies
where \(\overline{W} (t_0) = 0\). Using the same arguments as in the proof of Theorem 1, we obtain
so that \(\overline{W}(t) \le 0\), or equivalently \(V(t) \le W(t)\). \(\square \)
Rights and permissions
About this article
Cite this article
Tanwani, A., Brogliato, B. & Prieur, C. Stability notions for a class of nonlinear systems with measure controls. Math. Control Signals Syst. 27, 245–275 (2015). https://doi.org/10.1007/s00498-015-0140-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00498-015-0140-7