Spatial models for probabilistic prediction of wind power with application to annual-average and high temporal resolution data

Abstract

Producing accurate spatial predictions for wind power generation together with a quantification of uncertainties is required to plan and design optimal networks of wind farms. Toward this aim, we propose spatial models for predicting wind power generation at two different time scales: for annual average wind power generation, and for a high temporal resolution (typically wind power averages over 15-min time steps). In both cases, we use a spatial hierarchical statistical model in which spatial correlation is captured by a latent Gaussian field. We explore how such models can be handled with stochastic partial differential approximations of Matérn Gaussian fields together with Integrated Nested Laplace Approximations. We demonstrate the proposed methods on wind farm data from Western Denmark, and compare the results to those obtained with standard geostatistical methods. The results show that our method makes it possible to obtain fast and accurate predictions from posterior marginals for wind power generation. The proposed method is applicable in scientific areas as diverse as climatology, environmental sciences, earth sciences and epidemiology.

1 Introduction

In a society increasingly concerned with sustainability, the share of wind energy in total installed power capacity has grown rapidly in recent years around the world. For example, Denmark has the largest proportion of wind energy capacity relative to the volume of electricity consumption and the Danish government aims at having 50 % of the energy demand met by wind power by 2025 (Tastu et al. 2011). The main expected benefit from using wind power as a source of energy instead of fossil fuels is the reduction of carbon emissions. However, advanced forecasting methodologies are necessary to address issues related to the limited predictability of wind power generation. Increasing the quality of wind energy forecasts is not only important in order to efficiently handle the energy demand (Katzenstein et al. 2010), but it also increases the revenues from the electricity market, with the optimization of bidding strategies (Pinson et al. 2007).

From a statistical perspective, accurately predicting wind power and quantifying the uncertainties of the predictions at a regional scale is a challenging problem. Indeed, the statistical distribution of wind power data is characterized by the presence of complex temporal and spatial trends that are not well encompassed by stationary models. Also, the intermittent nature of wind leads to a spike at zero in the empirical distribution for high temporal resolutions (e.g. 15 min interval), which is difficult to model.

Studies on the medium-term and short-term forecasting of wind speed and wind power have received a lot of attention lately. Predictions of wind speed are ultimately in order to predict power; thus, there is a strong link to power, even when assessing the quality of wind speed predictions. The reader should note that it is common to have an overlap between wind speed and wind power in the literature. Based on this loose behaviour, we talk interchangeably here about wind speed and wind power. A common approach when the focus is on a single wind farm based on local measurements only, is related to a time-series framework that usually assumes a Gaussian distribution for the wind speed response. One of the first proposals in the literature was published in Brown et al. (1984) and uses auto-regressive moving average (ARMA) models for wind speed observations at lead times of between a few hours and a few days. The following year, Bossanyi (1985) used a Kalman Filter to predict wind speed at a one-minute resolution with the last six values as input, and observed an improvement in the RMS error over persistence for the prediction of the next time step of up to 10 %. Some years later, Daniel and Chen (1991), on the other hand, used stochastic simulation and forecasting models of hourly averages of wind speeds, taking into account the autocorrelation, non-Gaussian distribution and diurnal non-stationarity, and fitted an ARMA process to wind speed data. On a regional scale, Shih (2008) assessed periodic diurnal components and prevailing wind directions of wind speed time series in Taiwan using spectral analysis.

Recently, in a more general set up, Gneiting et al. (2006) introduced the regime-switching space-time model that identifies the atmospheric regime at the wind energy site and fits a conditional predictive model for each regime providing probabilistic forecasts of wind speed data. This approach deals with non-Gaussianity and with the discontinuity at zero by making use of a truncated normal distribution. To deal with discrete probability masses and the fact that normalized wind power is bounded between zero and one, Pinson (2012) applied the generalized logit-normal distribution with a potential concentration of probability mass at the bounds of the unit interval [0, 1] to forecast wind power fluctuations at single wind farms.

The methods mentioned above use only historical data at a single site. Because the spatial aspect of the problem is disregarded, these methods do not provide a straightforward way to extrapolate predictions at un-monitored locations. Moreover, wind power forecasting models developed for one location do not match the other sites due to, for example, change in terrain, different wind speed patterns and atmospheric factors. It is therefore not straightforward to transpose the results to other locations. In this sense, developing a portable and general model that mimics the spatial dependence structure and gives an overview of power generation at all wind power generation sites over a region is a timely objective.

Several spatial interpolation techniques are available to predict the wind speed in locations where data is not available. Luo et al. (2008) studied seven methods to estimate the daily mean wind velocity surface showing that kriging methods produce more accurate results than deterministic techniques on a country level. Joyner et al. (2015) compared the number of high-error stations produced when interpolating stations from wind data using ordinary kriging and cokriging. A geographic information system (GIS) based approach is used to assess wind resources in India and Poland in Hossain et al. (2011) and Sliz-Szkliniarz and Vogt (2011), respectively. Cellura et al. (2008) dealt with spatial estimation of the wind fields in Sicily by using neural kriging modeling. Etienne et al. (2010) predicted extreme wind speed with a combination of GIS techniques and Generalized Additive Models.

The purpose of the present paper is to propose statistical models for wind power generation that incorporate the spatial features of all the wind farm locations and yield calibrated predictive distributions with a minimum amount of computational effort. Reliability, also referred to as calibration, of probabilistic forecasts is assessed with reliability diagrams. A calibrated forecast should have the observed levels matching the nominal levels for specific quantile forecasts. Reliability is considered as the main required property of probabilistic forecasting (Gneiting et al. 2007) since it is used as input for decision problems and a probabilistic bias in the forecasts would yield poor operational decisions.

We use conventional kriging as a benchmark method for predicting the annual average wind power generation and high temporal resolution of wind power generation. This is one of the standard techniques for spatial interpolations, as described in Cressie (1988). Although kriging is an optimal method when the data follows a Gaussian distribution, it has proved to be a robust method under a range of conditions (Deutsch and Journel 1992). It can provide an efficient way to linearly interpolate nearby observations and thus lead to an estimation of wind power generation in each station; exclusively based on the mean and covariance structure of the Gaussian field.

In a first step, we focus on a model describing spatial variation of annual average wind power generation. We use a hierarchical spatial model based on a skewed continuous distribution with a stochastic, spatially structured mean that depends on the covariate. The spatial structure is captured by a latent Gaussian random field with a Matérn covariance function. In a second step, we propose a model tailored for wind power generation data with high temporal resolution. This type of scenario is of relevance for a number of operational problems where wind power generation is only observed at a limited number of wind farms, while decision-making problems may require an overview of power generation at all sites over a region. This setting is modelled with a mixture of degenerated distributions at zero and a skewed continuous distribution for the non-zero values. The distributions share a Gaussian random field with a Matérn covariance function.

Note that for these models, the posterior marginals are not available in closed form due to the non-Gaussian response variables. Departure from normality can easily be handled, but comes at a computational cost (Diggle et al. 1998). To issue probabilistic forecasts, we use an integrated nested Laplace approximation (INLA) (Rue et al. 2009) as an alternative to MCMC methods, and directly compute approximations to the posterior marginals. The resulting predictions are evaluated on a case study based on wind farms located in the western part of Denmark, while comparing the results from our approach to those from the ordinary kriging method.

Although this paper is motivated by the problem of spatial prediction of wind power generation, the solution developed here is relevant to many spatial prediction problems in earth and environmental sciences involving non-Gaussian data.

The remainder of this article is organized as follows. In Sect. 2, we give details of the data wind power data set used as a case study in order to show a realistic view of the methods proposed in this paper. In Sect. 3, we first describe the kriging method used here as benchmark. Then we present the hierarchical spatial model for predicting annual average wind power generation as well as the model tailored for wind power generation with high temporal resolution. We eventually explain how to perform inference and prediction with such models. A detailed explanation of the methods used for evaluation is given in Sect. 4. In Sect. 5, we present results for the probabilistic prediction of annual average and high temporal resolution of wind power generation, and compare our method with kriging. Section 6 contains a discussion of the limitations and possible extensions of our method and draws conclusions to our work.

2 Western Denmark wind power data

We consider a data set consisting of wind power generation measurements in wind farms located in the western part of Denmark. Each measurement is the temporal average power over a 15-min time step. The period covered ranges from January 2006 to March 2012. The distances between the wind farms range between 1 and 310 km.

The amount of wind power produced at a wind farm depends on its capacity, which is the maximum output when all turbines operate at their maximum nominal power. Since most of the wind farms have different capacities, and in order to facilitate comparisons between data sets, we normalize the wind power data by dividing all the measurements by the maximum nominal power value of each specific wind farm.

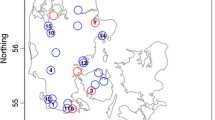
We start by modelling the annual average wind power generation in the year of 2010, where average wind power is obtained by averaging the 15-min normalized power output at each of 349 wind farms in 2010, resulting in purely spatial data. The year of 2010 was chosen for no specific reason to illustrate the proposed methods and the other years gave similar results. Note that here, in contrast with the scenario for the wind power at high temporal resolution, the large amount of zero measurements is not present, since these are averaged out with all the measurements at that specific station over 2010. A map of the normalized annual average wind power generation data set for 2010 is shown in Fig. 1. Thus, a value of 0.4 indicates that the annual average wind power generation for that specific wind farm is 40 % of the highest measurement obtained for that wind farm in 2010.

Next, to illustrate the methodology for modelling wind power generation at high temporal resolution, we fit the model separately to the data of each time step from the first day of every month in 2010. Please note that the remaining days and years gave similar results. Taking measurements from the first day of each month during 2010 results in $4 \times 24 \times 12 = 1152$ time steps. Since 165 of the 1152 time steps contain a large number of zero measurements, which results in problems during the estimation when using the R-INLA package, we used the remaining 987 time steps in our analysis, so that, in total, we have measurements from 349 wind farms over 987 time steps during the year of 2010.

Figure 2 shows the observed relative frequency of observations with wind power generation greater than zero for the first day of each month of 2010. In each plot, we calculate the relative frequency for wind farms $1, \ldots , 349$, by dividing the number of observations with power produced greater than zero by the total number of observations in a day. As we can see from this plot, in 2010, July, August and November had lower empirical probability of producing wind power, meaning that the data sets for these months contain a larger number of zeros.

Fig. 1

Normalized annual average wind power in 2010

Fig. 2

Histogram of the relative frequency of wind power generation greater than zero over the 349 wind farms in Denmark in the first day of each month of 2010. The relative frequency of wind power generation greater than zero for each wind farm is calculated as the number of observations with wind power generation greater than zero divided by the total number of observations in a day

3 Models and prediction methods

In this section we start by describing the standard benchmark kriging. Next, we introduce two different spatial models, one for the annual average wind power generation and another for high temporal resolution of wind power generation. The section ends with the methods used to perform inference and obtain probabilistic forecasts.

3.1 Kriging as a benchmark model

Kriging is just the usual name to describe the best linear unbiased predictor for a spatial process $Z_i$ at location i (Matheron 1963). Although the kriging equations also hold for non-Gaussian processes, the kriging predictor coincides with the best linear unbiased predictor only when the process is Gaussian. Nevertheless, the kriging method is an attractive benchmark due to its robustness and simplicity in obtaining predictions. Examples of models for precipitation and air quality monitoring using kriging methods can be found in Atkinson and Lloyd (1998) and Ignaccolo et al. (2014), respectively.

Depending on how the mean of $Z_i$ is modelled, different versions of kriging can be derived. While in ordinary kriging the mean is assumed to be constant and unknown over the neighbourhood of the value to be predicted, in universal kriging models, the mean is a function of covariates.

Two types of kriging methods are used in this paper—ordinary kriging and universal kriging. For the universal kriging, we define the covariate $d_i$ as the distance from wind farm i to the closest neighbouring coordinate on the border of the west coast of Denmark. The initial idea of including this covariate was inspired by maps of Danish wind speed developed to assist the Danish municipalities in their planning work for wind-turbine installation. These maps show that the prevailing wind directions in Denmark are west and southwest. Since the covariate improved the predictions only for the annual average of wind power generation, we use ordinary kriging to model wind power generation at a high temporal resolution and universal kriging to model the annual average of wind power generation. For simplicity of notation, we refer to both ordinary and universal kriging as just kriging.

To obtain predictions at unobserved locations, we fit a parametric variogram to the data. Before fitting the parametric variogram, we need to divide the data into several bins by breaking up the distances between each of the points based on a lag size between the distances, and afterwards the actual semi-variogram value is calculated for the bins. We start by calculating a sample variogram from the data that depends only on the distance between the wind farms. Next, we fit a parametric variogram model to the binned data from the sample variogram with the sill being equal to the maximum estimate of the sample variogram. The estimation of the variogram model parameters is done by iteratively reweighted least squares, with weights equal to $N_h/h^2$ (Cressie 1985), where $N_h$ is the number of point pairs and h is the distance between the locations. The range is set to be equal to the maximum of the distance from the sample variogram divided by two, and a parametric Matérn covariance structure is assumed. The Matérn covariance function is a flexible model that contains as special cases many of the covariance functions used in spatial statistics and is given by

$$\Sigma (s, s') = \frac{\sigma ^2}{2^{\nu -1}\Gamma (\nu )}(\kappa ||s-s'||)^{\nu }K_{\nu }(\kappa ||s-s'||)$$

(1)

where $K_{\nu }$ is the modified Bessel function of second kind of order $\nu >0$, $\kappa$ can be used to select the range and $\sigma$ to achieve the desired marginal variance. The parameter $\nu$ is a smoothness parameter determining the mean-square differentiability of the underlying process. Although this parameter is fixed to 1 for computational reasons, it remains flexible enough to handle a broad class of spatial variation (Rue et al. 2009). Applications with fixed parameter $\nu$ include (Guillot et al. 2015; Cameletti et al. 2013; Munoz et al. 2013; Musenge et al. 2013). Detailed information on the Matérn covariance model can be found in Guttorp and Gneiting (2006) and Stein (1999).

We perform kriging using the R package gstat.

3.2 A spatial model for annual average wind power generation

Annual average wind power generation is obtained by averaging the power produced over 2010 at each wind farm. Although the distribution of annual average wind power does not have the problem of probability mass at zero and is less skewed than individual power, there is still the challenge that it is bounded below by zero and above by the maximum total capacity of the turbines. As a result, it is reasonable to generate predictions that lie inside this permissible range. We propose a hierarchical spatial model for annual average wind power generation. To ensure that the final predictions lie in the valid range, we use a Beta distribution with a stochastic mean that we model using a log-normal distribution including both covariates and a spatial structure which is captured by a latent Gaussian random field.

Let $Y_1, \ldots , Y_N$ be the annual average normalized wind power, where N is the number of spatial points. We use the following parametrization for the Beta distribution with parameters a and b,

$$m = \frac{a}{a+b}, \quad 0 <\,m\,<1 \quad {\text{ and }} \quad \phi =a+b, \quad \phi >0,$$

(2)

which implies that $a = m \phi$ and $b=(1 - m)\phi$. The distribution of $Y_i$ can be written, in the new parametrization, as

$$Y_i\sim{\text{Beta}}(m_i \phi , (1 - m_i)\phi ).$$

(3)

We define a linear predictor for the log of the mean of $Y_i$, i. e.,

$${{\text{ log }}}(m_i) = f(d_i) + x_i$$

(4)

where $d_i$ is the distance from wind farm i to the closest neighbouring coordinate on the border of the west coast of Denmark, to be thoroughly described in the following and $x_i$ is a value of a Gaussian random field.

First of all, the spatial correlation of the random field formed by the set of $x_i$’s in (4) is incorporated through a zero mean Gaussian random field ${\mathbf{{x}}}$

$${\mathbf{{x}}} \,\sim \,{\mathcal {N}} \left( {\varvec{0}}, \Sigma \right) .$$

(5)

The covariance function $\Sigma$ belongs to the Matérn family. Instead of the parametrization given in (1), we redefine the covariance function depending on the range, $r = \frac{\sqrt{8 \nu }}{\kappa }$

$$\Sigma (s, s') = \frac{\sigma ^2}{2^{\nu -1}\Gamma (\nu )}\Big ( \frac{\sqrt{8 \nu }}{r} ||s-s'||\Big )^{\nu } K_{\nu }\Big ( \frac{\sqrt{8 \nu }}{r} ||s-s'||\Big )$$

(6)

The range parameter r introduced in the correlation function is interpreted as the minimum distance for which the correlation between two locations becomes negligible.

Now, we turn towards the component $f(d_i)$ in (4). Let ${\mathbf{{d}}} = (d_1, \ldots , d_N)$, the vector of distances from each wind farm to the closest neighbouring coordinate on the border of the west coast of Denmark. We define ${\tilde{{\mathbf{d}}}}$ as a grouped version of ${\mathbf{{d}}}$ with groups indexed by $c = 1, \ldots , 25$ and components ${\tilde{d}}_c$’s. We obtain the groups by first ordering the values of ${\mathbf{{d}}}$ from the smallest to the largest, and then using bins of equal length with the groups set to the median of the covariates belonging to that group. Next, the effect of the covariate $d_i$ is modelled as a smooth function f, defined as

$$f(d_i) = \sum _{c=1}^{m} w_i[c] l_c(i)$$

(7)

where $w_i[c]$ is the cth component of the vector ${\mathbf{{w}}}_i$. We suppose that the vector ${\mathbf{{w}}}_i$ is a set of serially randomly correlated regression coefficients, normally distributed with mean 0 and covariance matrix Q. The vector ${\mathbf{{l}}}(i)$ forms the series of basis functions. The basis function ${\mathbf{{l}}}(i)$ could be chosen, for example, as the so-called spline or B-spline basis (Lindgren et al. 2011). However, here we explore the use of explanatory variables as the basis function. We define $l_c(i)$ equal to an indicator function equal to one if the covariate $d_i$ belongs to group ${\tilde{d}}_c$, and zero otherwise.

Moreover, we assume that the coefficients over the range of the covariate values have a first order random walk prior. The random walk model of order 1 for a vector $(u_1, \ldots , u_n)$ is constructed assuming independent increments:

$$\Delta u_i = u_i - u_{i+1} \sim N(0, \tau ^{-1})$$

(8)

In order to test the significance of the covariate ${\tilde{d}}_i$ in the model, we compare the error of prediction with and without the covariate. Since including the covariate results in a smaller error of prediction, we choose to include it in the model.

Using $Y_i$’s Beta distribution in (3), it follows that the likelihood is

$$\begin{aligned} {\text{ L }}({\varvec{\theta }}|{\mathbf {y}})= & {} \prod _{y_i=1}^{N} {\text{ Beta }}(y_i|m_i, \phi ) \nonumber \\= & {} \prod _{y_i=1}^{N} \frac{{\mathrm {\Gamma }}(\phi )}{\mathrm {\Gamma }(m_i \phi ){\mathrm {\Gamma }}( \phi -m_i \phi )} y_i^{m_i \phi -1}(1-y_i)^{\phi (1 - m_i) - 1} \nonumber \\ \end{aligned}$$

(9)

The smoothness parameter $\nu$ in the Matérn covariance is set to 1 as in Sect. 3.1. Moreover, the function f in (7) only depends on the parameter $\tau$ in (8). It follows that the vector of hyperparameters is given by

$${\varvec{\theta }} = \{ {\phi , \tau , \kappa , \sigma } \}.$$

Default log-Gamma priors are assumed for all the hyperparameters in the model. We obtain predictions for the model just described with the INLA methodology implemented in the R-INLA package to be described in Sect. 3.4.

3.3 A spatial model for high temporal resolution of wind power generation

This model is tailored for wind power generation at high temporal resolution. It has a competitive advantage over using a truncated Gaussian process to handle the bound at zero, as explained in Stein (1992). Instead, our model uses a Bernoulli distribution to model the large amount of zero measurements in the data set, and it makes use of a Gamma distribution to model the asymmetric distribution of the positive values. This specification has the advantage of a well-behaved likelihood function that factors into two independent terms, making calculations relatively simple. The first term has only the logit model parameters and the second term involves only the parameters of the Gamma distribution [see Eq. (14)]. To overcome the so-called intermittency problem, where areas with small values lie very close to areas with large values, there is an underlying Gaussian field that is part of the linear predictor of both distributions—Bernoulli and Gamma.

Different approaches exist to deal with applications in which data take nonnegative values but have a substantial proportion of values at zero. One approach is to model a zero-inflation parameter that represents the probability of having zeros, given that these zero measurements come from the same distribution as the non-zero values. An example is found in Hall (2000).

Alternatively, data containing an abundant amount of zeros can be modelled with two latent Gaussian processes. The first controls the probability of observing zero values, and the second governs the density distribution of non-zero observations. Examples of this type of model used to describe accumulated precipitation include Berrocal et al. (2008) and Kleiber et al. (2012). On the other hand, Baxevani and Lennartsson (2015) model simultaneously the occurrence and intensity of rainfall using a single latent Gaussian field and then the positive part of the process is considered to be observed up to a transformation of the observed data. Rainfall and precipitation share similar features with wind power data sets, since one could have long periods of dry days with no rainfall observation. Here, we consider that wind power generation is driven only by one latent Gaussian field that controls both the occurrence and the intensity. Moreover, the probability of having power generation greater than zero is modelled as a Bernoulli distribution with probability that depends on the latent Gaussian field.

The model used in this paper is often called a hurdle model. The hurdle model for count data was proposed in Mullahy (1986). One part of the model is a binary model, such as a logistic or a probit regression, for whether the response outcome is zero or positive. To estimate the level of the positive outcomes, the second part of the model consists of a truncated model that modifies an ordinary distribution by conditioning on a positive outcome. Applications of similar models can be found in Pohlmeier and Ulrich (1995) and Gurmu (1997). Within the INLA framework, Serra et al. (2014) used a hurdle model to predict the occurrence of wildfires with point mass at zero followed by a truncated Poisson distribution for the non-zero observations.

In the second stage of our model, the distribution is a Gamma density for the non-zero values, which represents the amount of wind power generated. The Gamma distribution is a good choice for describing wind power values for several reasons. It provides a flexible representation of a variety of distribution shapes while utilizing only two parameters: the shape and the scale. It can range from exponential-decay forms for shape values near one, to nearly normal forms for shape values beyond 20 (Wilks 1990). In addition, a distribution that excludes negative values and is positively skewed is readily applicable for the analysis of wind power.

We start by defining a binary random variable $Z_i$ at location $i=1, \ldots , N$ which depends on the generation of wind power

$$Z_i=\left\{ \begin{array}{ll} 1,&\quad {\text{if}} \, y_i>0,\\ 0, &\quad {\text{ otherwise }}. \end{array}\right.$$

where $y_i$ is the observed wind power generation at wind farm i. We assume that $Z_i$ follows a Bernoulli distribution with parameter $p_i$

$$Z_i\sim{\text{Bern}}\left( p_i\right)$$

(10)

where $p_i$ is the probability of having wind power generation greater than zero at wind farm i and is modeled as

$${\text{ logit }}\left( p_i\right) = \alpha _z + x_i$$

(11)

with $\alpha _z$ being the intercept and $x_i$ an observation from a latent Gaussian random field with Matérn covariance as defined in (5). Then, conditional on the presence or absence of wind power, we model the amount of wind power generation at station i

$$Y_i|Z_i>0\,\sim\,{\text{Gamma}}\left( \phi , \frac{\phi }{m_i}\right)$$

(12)

with the expected value $m_i$ at wind farm i, defined as

$$\quad m_i = \exp \left[ \alpha _y + \beta _y x_i\right]$$

(13)

Finally, $\alpha _y$ is the intercept and $\beta _y$ the scaling parameter for $x_i$, which is defined in (11). The vector of the parameters to be estimated is given by

$${\varvec{\theta }} = (\alpha _z, \alpha _y, \beta _y, \phi , \kappa , \sigma )$$

The joint likelihood function is given by the product of the likelihood for the occurrence and the amount as

$$\begin{aligned} {{\text{ L }}}({\varvec{\theta }}|{\mathbf {z}},{\mathbf {y}})= & {} \prod _{z_i=0} {\text{ Bern }}(z_i|p_i) \nonumber \\&\prod _{z_i=1} {\text{ Bern }}(z_i|p_i) {\text{ Gamma }}(y_i|m_i, \phi ) \nonumber \\= & {} \prod _{z_i} {\text{ Bern }}(z_i|p_i) {\text{ Gamma }}(y_i|m_i, \phi )^{z_i} \nonumber \\= & {} \prod _{z_i} {p_i}^{z_i}(1-p_i)^{1-z_i} \nonumber \\&\Big [\frac{1}{{\mathrm {\Gamma }}(\phi )} \Big (\frac{\phi }{m_i} \Big )^{\phi } {y_i}^{\phi -1} {{\text{ exp }}} \Big ( - \phi \frac{y_i}{m_i} \Big ) \Big ]^{z_i} \end{aligned}$$

(14)

The binary variables $z_i$ for $i = 1,2, .., N$ are treated as observed variables in this model. We use the default values for the prior parameter, where a log-Gamma prior is assumed for $\kappa$ and $\phi$ and a Normal prior with a fixed vague precision is assumed for the fixed effects $\alpha _z, \alpha _y$ and $\beta _y$.

Once again, we obtain predictions for the model just described with the INLA methodology implemented in the R-INLA package to be described in Sect. 3.4.

3.4 Inference and prediction

Recall that the ultimate goal here is to obtain prediction and the corresponding uncertainty of wind power generation at unobserved locations. In this section, we explain how to do the parameter inference and obtain probabilistic prediction using the models described in Sects. 3.2 and 3.3.

When the focus is on prediction, latent Gaussian models can easily become computationally expensive as the cost of inverting dense covariance matrices increases cubically with the number of observed locations. A recent breakthrough alternative was proposed in Rue et al. (2009) and Lindgren et al. (2011). The former develops a framework for Bayesian inference in a broad class of models enjoying a latent Gaussian structure. The latter bridges a gap between Gaussian Markov random fields (GMRF) and Gaussian random fields theory and makes it possible to combine the flexibility of Gaussian random fields for modelling and the computational efficiency of GMRF for inference. The method of Lindgren et al. (2011) specifies a spatial model from a stochastic partial differential equation (SPDE) formulation instead of explicitly defining the covariance function. The key point of the SPDE approach is the finite element representation of the Matérn field that establishes the link between the Gaussian random field and the GMRF defined by the Gaussian weights to which a Markovian structure can be given. In particular, it is possible to find an explicit mapping of the Matérn covariance function of the Gaussian random field to the elements of the precision matrix Q of the GMRF with a computational cost of O(n). References on the accuracy of the INLA/SPDE approach in spatial statistics, which has been widely validated, can be found in Lindgren et al. (2011), Simpson et al. (2012) and Martins et al. (2013).

Specifically, the Gaussian field ${\mathbf{{x}}}$ with Matérn covariance is a solution to the linear SPDE

$$(\kappa ^2 - \Delta )^{\alpha /2} {\mathbf{{x}}} = {\mathcal {W}}, \quad \alpha = \nu + D/2, \kappa>0, \nu >0,$$

(15)

where D is the spatial dimension and $(\kappa ^2 - \Delta )^{\alpha /2}$ is a pseudo-differential operator defined in terms of its spectral properties (Lindgren et al. 2011). The random Gaussian field ${\mathbf{{x}}}$ is then approximated by a linear combination of basis functions and random weights

$${\mathbf{{x}}} = \sum _k \psi _k w^{*}_k$$

(16)

The random weights ${{\mathbf {w}}^* = (w^{*}_1 , \ldots , w^{*}_m})$ in (16) determine the values of the field at the vertices, and the values in the interior of the triangles are determined by linear interpolation. The full distribution of the solution to the SPDE in (15) is determined by the joint distribution of the weights in (16) (Lindgren et al. 2011).

Subsequently, the posterior estimates of parameters and hyperparameters are computed using INLA (Rue et al. 2009). INLA approximates the integral involved in the calculation of the marginal posterior distributions of the hyperparameters by Laplace approximation while the latent field is calculated using a Gaussian approximation evaluated at the mode of the posterior distribution.

We use the R-INLA package to perform inference and prediction. For more information on the package see http://www.r-inla.org.

Model fitting and prediction of the spatial random effect are done simultaneously on a grid of locations. The grid with the prediction locations, usually called mesh, is a partition of the region into triangles that discretizes the random field at m nodes. The mesh is constructed by defining the basis function $\psi _1, \dots , \psi _m$ in (16) for every node in the triangulation so that they are equal to one in the mesh nodes and zero in all other nodes. The advantage of the triangulation over a regular grid is the possibility to have smaller triangles where there is the need for higher accuracy of the field representation, so the observation locations are dense, and larger triangles where there is no data and spending computational resources would be wasteful (Lindgren 2012).

Figure 3 shows the triangulation using the western Denmark data described in Sect. 2. The red dots denote the 349 wind farms in our data set. Note that the area of Denmark where we have data includes several islands. In order to construct the triangulation, we form one single polygon that represents the global boundary of the western part of Denmark (blue line at Fig 3).

Fig. 3

The western Denmark triangulation. Red denotes the 349 wind farms where we have data. The blue line is the boundary that covers all the islands in the western part of Denmark

We use a copula-based correction for the INLA (Ferkingstad and Rue 2015). The correction is especially useful for generalized linear mixed models that involve the Binomial or Poisson distributions, where inaccuracies in the Laplace approximation can occur because of the very low degree of smoothing in some models. Following the Bayesian framework in Rue et al. (2009), it is necessary to approximate the full joint distribution of the latent field given the parameters and the observations in order to compute the posterior marginal distributions of the parameters and the latent field given only the data. This approximation is usually done in INLA using a Gaussian approximation found by matching the mode and the curvature at the mode of the posterior marginal distribution of the latent field. However, approximations using skew normal densities based on a second Laplace approximation are shown to be more accurate than the Gaussian approximation (Rue et al. 2009). Ferkingstad and Rue (2015) shows how to use the Gaussian copula to construct an approximation to the full joint distribution that retains the dependence structure of the Gaussian approximation, while having the improved marginals from skew normal densities. The correction has been added as part of the R-INLA and adds minimally to the running time of the algorithm.

4 Evaluation framework

To assess the quality of the predictive distributions for the annual average and high temporal resolution of wind power generation, we use k-fold cross validation with $k=4$ for the three methods described in Sect. 3. The idea of the k-fold cross validation is to split the data into k roughly equal-sized parts. For each split, we fit the model to the remaining $k-1$ parts of the data and calculate the prediction error of the fitted model when predicting the k-th part of the data. We repeat this procedure 50 times to reduce sampling bias and variance. The prediction error is obtained by combining the four estimates from the 50 data sets. Overall, 5 to 10-fold cross-validation is recommended as a good compromise between bias and variance (Breiman and Spector 1992; Kohavi 1995). However, here we choose 4-fold cross-validation since we have a large sample size and want to reduce computational costs.

The cross-validation estimate of the prediction error is measured through the continuous ranked probability score (CRPS), which is a strictly proper scoring rule for the evaluation of probabilistic forecasts of a univariate quantity (Gneiting and Raftery 2007). The CRPS is negatively oriented, i.e., the smaller the better, and is defined as

$${\text{ CRPS }}(P, x) = \int ^{\infty }_{-\infty } (P(y) - I(y \ge x))^2 dy$$

(17)

where P is the cumulative distribution function of the density forecast and x is the normalized observed wind power.

In addition, we obtain the point forecast for the normalized wind power at a specific location as the mean of the predictive distribution. We calculate the root mean squared error (RMSE) and bias of the point forecasts to compare prediction performances. Note that since RMSE is a quadratic loss function, the mean of the predictive distribution is the optimal point predictor (Banerjee et al. 2005). The RMSE and bias are defined as follows

$${\text{ RMSE }} = \sqrt{\frac{1}{N R} \sum _{i=1}^{N} \sum _{j=1}^{R} (y_{ij} - \hat{y}^{-k(i)}_{ij})^2 }$$

(18)

$${\text{ bias }} = \frac{1}{N R} \sum _{i=1}^{N} \sum _{j=1}^{R} (y_{ij} - \hat{y}^{-k(i)}_{ij})$$

(19)

where N is the number of data points, R is the number of replicates in the k-fold cross-validation, k(i) is the function that maps the observation i to the group k and $\hat{y}^{-k(i)}_{ij}$ is the mean of the posterior predictive distribution when the model was fitted with the data set excluding the k(i) part.

Similarly, using the median of the density forecasts as the point forecast, we compute the mean absolute error (MAE). Here, the point forecast that minimizes the MAE is the median of the predictive distribution, since MAE is a symmetric linear function in contrast to the RMSE (Fraley et al. 2010; Pinson and Hagedorn 2012).

$${\text{ MAE} } = \frac{1}{N R} \sum _{i=1}^{N} \sum _{j=1}^{R} |y_{ij} - \hat{y}^{-k(i)}_{ij}|$$

(20)

To formally test for a significant difference between the predictions made for two spatial fields, we apply the spatial prediction comparison test (SPCT) introduced in Hering and Genton (2011). The null hypothesis to be tested is that of equal predictive ability on average in terms of a loss function, such as absolute differences, squared differences, as well as skill score functions. Gilleland (2013) proposed two new loss functions to the SPCT, the first is based on distance maps and the second on image warping.

The SPCT yields a statistical test that accounts for spatial correlation without imposing any assumption on the underlying data or on the resulting loss differential field. The loss differential field is a field giving the straight difference between the two loss functions calculated for each of two forecasts. We are interested in the average of the loss differential field, which is asymptotically Normal distributed (Hering and Genton 2011). Because the loss differential field is likely to have a strong spatial correlation, the standard error for its mean is calculated from the variogram. Here, we use an isotropic exponential variogram to fit the data. Moreover, if a trend on the data is suspected, it should be removed before applying the SPCT, since the mis-specification of the trend can result in a test for prediction comparison that is undersized or oversized. We perform ordinary least squares (OLS) to estimate and, if necessary, remove the trend from our data. Based on the large p-values of the regression coefficients in the OLS that were obtained when we fitted the data from the annual average power output, we conclude that there is no significant trend to be removed in this case.

The SPCT is implemented in the R package SpatialVx, which is used here to obtain p-values for the difference in RMSE, CRPS, bias and MAE between the models described in Sect. 3.

We assess the predictive performance with reliability and sharpness diagrams. Reliability represents the ability of the forecasting system to match the observation frequencies. Ideally, the nominal coverage rates, which is the proportion of times that the cumulative distribution of a random variable is below a threshold, and the observed frequencies would be the same, resulting in points aligning with the diagonal. For example, for a nominal coverage rate $\alpha =0.05$, it is expected that 5 % of the observations are smaller than the predictive quantile at nominal level 0.05. However, a reliable forecast is not useful if it is not informative. The sharpness diagram gives an indication of the spread of the predictive distributions. It is measured by the average interval size in the case of predictive intervals, which should be as tight as possible for a sharp forecast (Gneiting et al. 2007).

In order to construct reliability diagrams, we start by introducing an indicator variable ${\mathcal {I}_{i,j}}^{(\alpha )}$, which is defined for a quantile forecast ${\hat{p}}_{i,j}^{(\alpha )}$ made at wind farm i and replicate j with observed value $p_{ij}$ as follows

$${\mathcal {I}_{i,j}}^{(\alpha )} = {\left\{ \begin{array}{ll} 1 & \quad {\text {if }} \, p_{ij} \le {\hat{p}}_{i,j}^{(\alpha )} \\ 0, &\quad {\text{otherwise}}\\ \end{array}\right. }$$

The indicator variable ${\mathcal {I}_{i,j}}^{(\alpha )}$ tells whether the actual outcome lies below the quantile forecast (hits) or not (miss). Next, denote $n_{1}^{(\alpha )}$ the sum of hits and $n_{0}^{(\alpha )}$ the sum of misses over all the realizations

$$n_{1}^{(\alpha )} = \sum ^{N}_{i=1} \sum ^{R}_{j=1} {\mathcal {I}_{i,j}}^{(\alpha )} \quad {\text{ and }} \quad n_{0}^{(\alpha )} = N - n_{1}^{(\alpha )}$$

An estimation ${\hat{a}}^{(\alpha )}$ of the actual coverage $a^{(\alpha )}$ is then obtained by calculating the mean of ${\mathcal {I}_{i,j}}^{(\alpha )}$ over the N wind farms and R replicates in the validation set.

$${\hat{a}}^{(\alpha )} = \frac{1}{N R} \sum _{i=1}^{N} \sum ^{R}_{j=1} {\mathcal {I}_{i,j}}^{(\alpha )} = \frac{n_{1}^{(\alpha )}}{n_{1}^{(\alpha )} + n_{0}^{(\alpha )}}$$

(21)

This approach to the evaluation of prediction intervals was proposed in Baillie and Bollerslev (1992) and McNees and Fine (1995). Consistency bars for the reliability diagram with 95 % confidence level are computed by simulating a Binomial distribution with parameters N equal to the corresponding number of wind farms, and p, the probability of success, equal to the nominal level $\alpha$.

In the sharpness diagram, for each nominal quantile and each station, we can obtain the length of the central predicted interval. Central predictive intervals are centered in probability around the median. For example, the value at the 60 % nominal coverage is the predicted value at the 80 % quantile minus the predicted value at the 20 % quantile. The final predicted interval size is the average size of the predicted intervals over all the wind farms and replicates as follows

$${\bar{\delta }}^{(\alpha )} = \frac{1}{N R} \sum _{i=1}^{N} \sum ^{R}_{j=1} \delta _{i,j}^{(\alpha )} = \frac{1}{N R} \sum _{i=1}^{N} \sum ^{R}_{j=1} \Big ( {\hat{p}}_{i,j}^{(1 - \alpha /2)} - {\hat{p}}_{i,j}^{(\alpha /2)} \Big )$$

(22)

We complete this section by explaining how to assess the reliability of the induced probability forecasts for the occurrence of wind power in the model shown in Sect. 3.3. We compute the observed relative frequencies in 21 equally spaced bins between 0 and 1. For each predicted value, it is established which of the bins the value falls into. The corresponding observed relative frequency is the number of times the event happens, given that the predicted probability belongs to a specific bin, divided by the total number of predicted values in that bin. Each bin is represented by a single forecast probability, which is chosen to be the average of the predicted values over the bin. Bröcker and Smith (2007) mentions the advantages of considering the average instead of the popular choice of the arithmetic center of the bin.

5 Results

We now present verification results for the probabilistic prediction of annual average and high temporal resolution of wind power generation after k-fold cross-validation based on the evaluation framework described in Sect. 4.

5.1 Verification results for annual average wind power generation

In this section, we show results obtained from modelling the annual average wind power generation in the year of 2010, where average wind power is obtained by averaging the power output at each of the 349 wind farms in the western part of Denmark. We compare the predictions obtained with the Beta model with covariates fitted with the INLA/SPDE approach described in Sect. 3.2 with kriging in Sect. 3.1. Table 1 shows summary measures of predictive performance for annual average wind power generation, which are fully described in Sect. 4. The large p-values in this table indicate that we do not reject the hypothesis of equal predictive ability on average in terms of RMSE, CRPS, Bias and MAE between the Beta model with covariate fitted with the INLA/SPDE approach and kriging. This is not surprising given that here, since the data is averaged over an entire year, the individual noises are smoothed out and the distribution becomes closer to Gaussian.

We assess reliability and sharpness of the predicted annual average wind power generation through the diagrams in Fig 4. In this figure we can see a comparison between the Beta model with covariates fitted with the INLA/SPDE approach and kriging of the reliability diagram together with the respective consistency bars (left) and sharpness diagram (right). The Beta model tends to overestimate the annual average wind power generation for quantiles larger than 0.25, which results in a reliability curve below the diagonal. However, this model also has a considerably smaller prediction interval, as shown in the right plot of the same figure. We remark that the consistency bars in this figure are constructed without considering the replicates of the k-fold validation as part of the total number of observations, since they are not independent realizations of the process. The method of combining replicates of predictions when building consistency bars for the reliability diagram should be investigated further to have consistency bars of correct size in Fig. 4.

In summary, the results for modelling the annual average of wind power generation show that kriging should be preferred over the Beta model with covariates fitted with the INLA/SPDE approach. Both methods present similar results, while kriging is easier to set up and has lower computational cost. While kriging takes approximately 0.05 s to fit and get point predictions at one replication and 1-fold in a single processor Intel Core i7-4600U/2.10 GHz machine, the INLA method takes approximately 20.08 s to get inference and density of the predictions in the same machine.

Table 1 Root mean square error (RMSE), continuous ranked probability score (CRPS), bias and mean absolute error (MAE) with respect to the maximum capacity (in percentage) for annual average wind power generation using kriging and the Beta model with covariate.

Fig. 4

Reliability diagram with respective consistency bars (left) and sharpness diagrams (right) for the annual average wind power generated in 2010

5.2 Verification results for high temporal resolution of wind power generation

We now present verification results for predicting wind power at a high temporal resolution, considering data from 2010 in the western part of Denmark. We fit the model separately to each of the 987 time steps spread over 12 days, each day belonging to a different month in the 2010 calendar year. Then, we calculate the average of the results and scores from the individual prediction cases. Here, we compare the models described in Sects. 3.3 and 3.1.

Figures 5 and 6 show an example of normalized wind power data at high temporal resolution in 2010, together with the predictive maps of the mean and the standard deviation for the western part of Denmark. In Fig 5, the left plot is the observed wind power after normalization, the middle plot corresponds to the predicted mean obtained with kriging and the plot on the right corresponds to the hierarchical hurdle gamma model fitted with the INLA/SPDE approach. From Fig 5, we can see that the Gamma model is able to predict larger mean values of normalized wind power than the kriging. The predicted standard deviations are shown in Fig 6. In this figure, the left plot is produced with kriging and the plot on the right corresponds to the hierarchical hurdle Gamma model fitted with the INLA/SPDE approach. While the standard deviation from the Gamma model is larger where the predicted mean value is also larger, the kriging has a large standard deviation everywhere except where the observations are placed.

We start by presenting the verification results for the observed measurements that are greater than zero. In Table 2, we compare summary measures of predictive performance for wind power greater than zero obtained using the hurdle gamma model fitted with the INLA/SPDE approach which is described in Sect. 3.3 and kriging described in in Sect. 3.1. The hierarchical hurdle Gamma model produces significantly better predictions on average in terms of RMSE, CRPS and MAE than kriging. The superiority of the hierarchical spatial method over the kriging may stem from a lack of flexibility of the latter, as it does not consider the point mass at zero in the wind power distribution and is optimal only when data is Gaussian distributed. In contrast, the hurdle Gamma model attempts to accommodate wind occurrences with a Bernoulli distribution and wind power magnitude using the Gamma distribution, where a shared latent process is included to handle spatial correlation between wind farms in both distributions.

On the other hand, kriging is considerably faster than the model fitted with the INLA/SPDE approach. It takes approximately 0.06 s to estimate one replication and 1 fold, while the hurdle Gamma model fitted with INLA takes approximately 44.4 s to get inference and density of the predictions in a single processor Intel Core i7-4600U/2.10 GHz machine. The trade-off between a method that offers more accurate predictions with a sharper predictive density and a method that is simpler to set up and requires less computational effort will most likely depend on the type of application.

The plots in Fig. 7 show a comparison between the hierarchical hurdle Gamma model and kriging in terms of reliability (left) and sharpness (right) for a power output greater than zero. Kriging has a curve close to the diagonal, while the hierarchical hurdle Gamma model has a sigmoid-shaped curve, which could be due to a violation of the model assumptions. In this scenario, we do not need consistency bars because of the large sample size, since we have 349 wind farms and 50 replicates for each of the 987 time steps.

Figure 8 shows the histogram for the wind power measurements greater than zero together with their predictions, which is the mean value of the posterior distribution, using the two methods of comparison: kriging and the hierarchical hurdle Gamma model. The positive values of wind power are clearly not Gaussian distributed. It can also be observed that the kriging method (second plot) predicts less values close to one in comparison to the hurdle Gamma model (third plot) and in comparison with the true distribution (first plot). In fact, the proportions of observations, kriging predictions and Gamma model predictions that exceed 0.75 are 0.0207, 0.0006 and 0.0131 respectively.

Recall that the hierarchical hurdle Gamma model fitted with the INLA/SPDE approach additionally gives predictions of the Bernoulli-distributed random variable that maps the occurrence of wind power generation. We assess the reliability of the probability predictions for the occurrence of wind power generation through the diagram in the bottom line of Fig 9. This plot shows the empirically observed frequency of wind power occurrence as a function of the binned forecast probability. The actual observed relative frequency is well approximated by the forecast probability, as the line in this plot lies close to the diagonal. The top plots in the same figure correspond to histograms of the empirical probability (left) and the predicted probability (right) of wind power occurrence. As we can see from the left plot, there are almost five-times as many time steps with generated power greater than zero than equal to zero. The histogram of the predicted probabilities on the right side shows the same tendencies, since most of the estimated probabilities of wind power occurrence are close to one.

Fig. 5

Example of normalized wind power data generated at a fixed 15 min interval from 2010 (left). Predicted mean of the normalized wind power obtained with kriging (middle) and with the hierarchical hurdle Gamma model (right)

Fig. 6

Predicted standard deviation of the normalized wind power obtained with kriging (left) and with the hierarchical hurdle Gamma model (right)

Table 2 Root mean square error (RMSE), continuous ranked probability score (CRPS), bias and mean absolute error (MAE) with respect to the maximum capacity (in percentage) of wind power generation at high temporal resolution when the wind power output is greater than zero using kriging and the hierarchical hurdle Gamma model

Fig. 7

Reliability (left) and sharpness (right) diagrams for wind power generation at high temporal resolution when the wind power output is greater than zero using kriging and the hierarchical hurdle Gamma model

Fig. 8

Histograms of the normalized wind power greater than zero (left), of the predicted wind power using kriging (middle) and of the predicted wind power using the hierarchical hurdle Gamma model (right)

Fig. 9

First line Histograms of the empirical probability (left) and the predicted probability (right) of wind power occurrence using the hierarchical hurdle Gamma model. Second line Reliability diagram for the probability of wind power occurrence using the hierarchical hurdle Gamma model

6 Discussions

We have presented statistical methods for obtaining probabilistic predictions of wind power generation at annual average as well as high temporal resolution (15 min averages) and we have compared the results from these methods with the benchmark kriging. In the first scenario, at any individual wind farm, the distribution of the annual average wind power generation is modelled with a Beta distribution, where the distance to the west coast of Denmark is used as a covariate and the spatial dependence between different locations is captured by a spatial Gaussian process with Matérn covariance. The second scenario builds on a hierarchical hurdle Gamma model, which is similar to well-known models for precipitation such as Berrocal et al. (2008) and Baxevani and Lennartsson (2015) in the sense that it is also a two-stage model with a Gaussian field to account for spatial correlation. However, our approach introduces a new Bernoulli-distributed random variable to account for the probability of wind power occurrence. The parameter p of this distribution depends on the Gaussian field and can be fully estimated. The continuous part of our two-stage model has a Gamma distribution where the mean depends on the same Gaussian field that is used for modelling p.

To perform inference and prediction, instead of using MCMC, we have used the novel INLA approach. We have shown that complex hierarchical spatial models are well suited to wind power data and can be implemented seamlessly under the SPDE approach that is implemented in the R-INLA library providing results in reasonable computational time.

We show results from case studies on the probabilistic prediction of annual average and high temporal resolution of wind power generation with wind farms from the western part of Denmark. While the Beta model approach showed similar results to the benchmark method, the hierarchical hurdle Gamma model resulted in predictive distributions that consistently outperformed the benchmark model in terms of the validation measures CRPS, RMSE, bias and MAE. The predictive distributions obtained from the hurdle Gamma model have increased sharpness, resulting in less reliability as compared to the kriging method. Therefore, a more accurate method for generating consistency bars in the reliability diagram should be considered to draw more solid conclusions about the reliability of the predictions from our method.

The models presented in this work could also be extended to the spatiotemporal domain by incorporating an extra term for the temporal effect such as an autoregressive component or by the introduction of a non-separable spatiotemporal structure. This would come with a computational cost, which would have to be assessed.