Probabilistic solution of floodplain inundation equation

Abstract

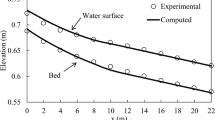
Uncertainty in bed roughness is a dominant factor in providing a sufficiently accurate simulation of floodplain flows. This study describes a method to compute the transition probability density distribution of time-varying water elevations where the evolutionary process is based on a conventional one-dimensional storage cell model with governing stochastic differential equation. By including the random inputs (or noise terms) of bed roughness and initial water depth, time-dependent and spatially varying probability density function of the water surface leads to a Fokker–Planck equation. The model’s performance is evaluated by applying it to shallow water flow with a horizontal bed. Sensitivity of model predictions to variations in the bed friction parameters is shown. By comparing the result of the proposed method with that of conventional Monte Carlo simulation, the advantage of the former as a method for density function prediction is confirmed.

Appendices

Appendix 1: Theoretical framework for a general stochastic system

The SDE models play a prominent role in a wide range scientific and professional fields, including meteorology, mechanics, engineering, biology, and finance. A general spatially varying stochastic process is described by a random vector ${\varvec{H}}({\varvec{x}},t)$, where x is the space coordinate vector of discretised grid cells over a planner slope and t is time. Its dynamical state is determined by

$$ {\dot{\varvec{H}}} = {\varvec{F}}({\varvec{H}},{\varvec{x}},{\varvec{\varPsi}}) $$

(12)

with the initial condition

$$ {\varvec{H}}_{0} = {\varvec{H}}({\varvec{x}},0) $$

(13)

where ${\varvec{H}} = (H_{1} ,H_{2} , \ldots ,H_{{n_{\text{d}} }} )^{\text{T}}$ is the state vector, n _d is the dimension of the state space, ${\varvec{F}} = (F_{1} ,F_{2} , \ldots ,F_{{n_{\text{d}} }} )^{\text{T}}$ is the operator vector, ${\varvec{\varPsi}} = (\varPsi_{1} ,\varPsi_{2} , \ldots ,\varPsi_{{n_{\text{e}} }} )$ is a random parameter vector with known PDF $p_{{\varvec{\varPsi}}} ({\varvec{\xi}})$, random vector ${\varvec{\xi}} = (\xi_{1} ,\xi_{2} , \ldots ,\xi_{{n_{\text{e}} }} )$, and n _e is the number of the random parameters involved. The system and the time evolution of H depend on the dynamic model F under consideration and the random parameter vector ${\varvec{\varPsi}}$, which includes the stochastic parameters characterising the system properties, as well as the external excitations. When the excitation is a stochastic process, Eqs. (12) and (13) represent a stochastic dynamical system with randomness originating from the excitations, the system properties, and the initial conditions.

For a wide range of problems, a more specific model that characterises a Markovian process is often adopted. In this work, it was obtained by decomposition of the operator vector F as:

$$ {\dot{\varvec{H}}}({\varvec{x}},t) = {\varvec{\varphi }}({\varvec{H}},{\varvec{x}},t) + {\varvec{G}}({\varvec{H}},{\varvec{x}},t){\varvec{W}}(t) $$

(14)

where ${\varvec{\varphi }}({\varvec{H}},{\varvec{x}},t)$ is a function vector representing the effects of some form of drift, ${\varvec{G}}({\varvec{H}},{\varvec{x}},t)$ is a function vector representing the effects of random diffusion, and W(t) is an n _e-dimensional Gaussian (or white) noise vector. Assuming that the white noise processes are mutually independent, the co-variance parameter matrix of W(t) will be a diagonal matrix with its diagonal terms equal to the variance of the white noise processes $W_{1} (t),W_{2} (t), \ldots ,W_{{n_{\text{e}} }} (t)$ and ${\varvec{D}} = (D_{11} ,D_{22} , \ldots ,D_{{n_{\text{e}} n_{\text{e}} }} )$.

Equation (14) can also be written in the form of the standard Itô equation (see Soong, 1973):

$$ {\text{d}}{\varvec{H}}({\varvec{x}},t) = {\varvec{\varphi }}({\varvec{H}},{\varvec{x}},t){\text{d}}t + {\varvec{G}}({\varvec{H}},{\varvec{x}},t){\text{d}}{\varvec{W}}(t) $$

(15)

with ${\text{E}}\left\{ {{\text{d}}{\varvec{W}}(t)} \right\} = {\varvec{0}}$ and ${\text{E}}\left\{ {\left[ {{\text{d}}{\varvec{W}}(t)} \right]^{2} } \right\} = 2{\varvec{D}}{\text{d}}t$.

The dynamic system described by Eq. (15) with the deterministic operators ${\varvec{\varphi }}$ and G and the random initial condition given by Eq. (13) is a probability preservative system and, with the PDF of H, i.e., $p({\varvec{H}},{\varvec{x}},t)$, satisfying the FPE (Soong 1973):

$$ \frac{{\partial p({\varvec{H}},{\varvec{x}},t\left| {{\varvec{H}}_{0} ,t} \right.)}}{\partial t} = - \sum\limits_{j = v}^{{n_{\text{d}} }} {\frac{\partial }{{\partial h_{v} }}\left[ {\varphi (h,{\varvec{x}},t)_{v} p} \right]} + \frac{1}{2}\sum\limits_{u,v = 1}^{{n_{\text{d}} }} {\frac{{\partial^{2} }}{{\partial h_{v} \partial h_{u} }}\left[ {(GDG^{T} )_{uv} p} \right]} $$

(16)

The term $(GDG^{T} )_{uv}$ is given by

$$ (GDG^{T} )_{uv} = \sum\limits_{k,l = 1}^{{n_{\text{e}} }} {D_{kl} G_{uk} ({\varvec{H}},{\varvec{x}},t)G_{vl} ({\varvec{H}},{\varvec{x}},t)} ;\;\left( {u,v = 1,2,\ldots,n_{\text{d}} } \right) $$

(17)

where G _uk and G _vl are components of ${\varvec{G}}({\varvec{H}},{\varvec{x}},t)$.

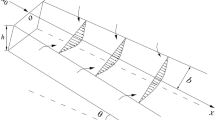
In this study, a stochastic flow depth evolution model is formulated based on the theoretical framework described above. The state function vector is derived using the one-dimensional storage cell model for floodplain flow (Bates and De Roo 2000). Thus, only one direction transport is considered to contribute to the flow surface changes, implying n _d = 1. In addition, for the sake of simplicity, only the characteristic bed roughness parameter is taken as a random parameter, implying n _e = 1.

Appendix 2: Derivation of Gaussian distribution of friction term

The Gaussian distribution provides a close approximation to the probability laws of many natural phenomena. In this study, it was used to represent a frequency distribution for the roughness coefficient. It has been widely used not only due to its greater flexibility and simplicity, but also because it can provide a good fit to field data. The Gaussian distribution function, which is a two-parameter function, for the floodplain roughness n is expressed mathematically as:

$$ f(n;\mu ,\sigma ) = \frac{1}{{\sqrt {2\pi } \sigma }}\exp \left[ { - \left( {\left( {n - \mu } \right)^{2} /2\sigma^{2} } \right)} \right] $$

(18)

where μ and σ are the mean and standard deviation parameters, respectively.

Assuming that the roughness n follows the Gaussian distribution, the density of Strickler coefficient N can be derived easily, as shown below.

$$ \begin{aligned} g(N;\mu ,\sigma ) & = \frac{f(N;\mu ,\sigma )}{{{\text{d}}N/{\text{d}}x}}\left| {_{{x = N^{ - 1} }} } \right. \\ & = - N^{ - 2} \frac{1}{{\sqrt {2\pi } \sigma }}\exp \left[ { - \left( {\frac{{\left( {N^{ - 1} - \mu } \right)^{2} }}{{2\sigma^{2} }}} \right)} \right] \\ \end{aligned} $$

(19)

It has been shown that N behaves according to the Gaussian distribution, but the scale parameter reduces by N ⁻² times.