Variational multiscale enrichment method with mixed boundary conditions for elasto-viscoplastic problems

Abstract

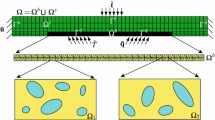
This manuscript presents the formulation and implementation of the variational multiscale enrichment (VME) method for the analysis of elasto-viscoplastic problems. VME is a global–local approach that allows accurate fine scale representation at small subdomains, where important physical phenomena are likely to occur. The response within far-fields is idealized using a coarse scale representation. The fine scale representation not only approximates the coarse grid residual, but also accounts for the material heterogeneity. A one-parameter family of mixed boundary conditions that range from Dirichlet to Neumann is employed to study the effect of the choice of the boundary conditions at the fine scale on accuracy. The inelastic material behavior is modeled using Perzyna type viscoplasticity coupled with flow stress evolution idealized by the Johnson–Cook model. Numerical verifications are performed to assess the performance of the proposed approach against the direct finite element simulations. The results of verification studies demonstrate that VME with proper boundary conditions accurately model the inelastic response accounting for material heterogeneity.

Appendix

This appendix section presents the details of $\mathbf{C} = \left( \frac{\partial \dot{\varvec{\varepsilon }}^{vp}}{\partial \varvec{\sigma } }\right)$ and $\mathbf{G} = \left( \frac{\partial \dot{\varvec{\varepsilon }}^{vp}}{\partial \varvec{\varepsilon }^{vp} }\right)$ that are illustrated in Sect. 4.1. For the clarity of presentation, the bold symbol in this section denotes vector notation. Recall the evoluation of plastic strain (Eq. (5)), the loading function [Eq. (6)] and the flow stress [Eq. (8)]. Define

$$\begin{aligned} F\equiv \frac{f(\varvec{\sigma }, \varvec{\varepsilon }^{vp})}{{\sigma _y}(\varvec{\varepsilon }^{vp}) } \end{aligned}$$

(60)

and

$$\begin{aligned} \mathbf{a}\equiv \frac{\partial f(\varvec{\sigma }, \varvec{\varepsilon }^{vp})}{\partial \varvec{\sigma }} =\sqrt{3} \frac{\partial \bar{{\sigma }}}{\partial \varvec{\sigma }} =\frac{\sqrt{3}}{2 \bar{{\sigma }}} \tilde{\varvec{\sigma }} \end{aligned}$$

(61)

where, in 3D case $\tilde{\varvec{\sigma }}$ is expressed in a vector format as:

$$\begin{aligned} \tilde{\varvec{\sigma }}=\left\{ {s_{xx}}, {s_{yy}},{s_{zz}},2{\sigma _{xy}},2{\sigma _{yz}},2{\sigma _{zx}}\right\} ^\mathrm{T} \end{aligned}$$

(62)

in which $s$ denotes deviatoric stress components. Consequently, the plastic strain evolution equation is expressed as:

$$\begin{aligned} \dot{\varvec{\varepsilon }}^{vp}=\gamma \left\langle F \right\rangle ^{q} \mathbf{a} \end{aligned}$$

(63)

and $\mathbf{C}$ becomes:

$$\begin{aligned} \begin{aligned} \mathbf{C} = \left( \frac{\partial \dot{\varvec{\varepsilon }}^{vp}}{\partial \varvec{\sigma } }\right)&=\gamma \left[ \left\langle F \right\rangle ^{q}\frac{\partial \mathbf{a}}{\partial \varvec{\sigma } } + q \left\langle F \right\rangle ^{q-1} \frac{\partial \left\langle F \right\rangle }{\partial f} \frac{\partial f}{\partial \varvec{\sigma } } \otimes \mathbf{a}\right] \\&=\gamma \left\langle F \right\rangle ^{q} \left[ \frac{\partial \mathbf{a}}{\partial \varvec{\sigma } } + \frac{q \left[ \text {sign}(F) +1\right] }{2 \left\langle f \right\rangle } \mathbf{a} \otimes \mathbf{a}\right] \end{aligned} \end{aligned}$$

(64)

From Eq. (61):

$$\begin{aligned} \begin{aligned} \frac{\partial \mathbf{a}}{\partial \varvec{\sigma } }=\frac{\sqrt{3}}{2 \bar{{\sigma }}} \mathbf{M}-\frac{\sqrt{3}}{3 \bar{{\sigma }}} \mathbf{a} \otimes \mathbf{a}; \mathbf{M}=\frac{\partial \tilde{\varvec{\sigma }}}{\partial \varvec{\sigma }} \end{aligned} \end{aligned}$$

(65)

In 3D case, $\mathbf{M}$ is expressed as:

$$\begin{aligned} \mathbf{M}= \left[ {\begin{array}{lllccc} \frac{2}{3}\, &{}\quad -\frac{1}{3}\, &{}\quad -\frac{1}{3}\, &{}\quad 0\, &{}\quad 0\, &{}\quad 0 \\ -\frac{1}{3}\, &{}\quad \frac{2}{3}\, &{}\quad -\frac{1}{3}\, &{}\quad 0\, &{}\quad 0\, &{}\quad 0 \\ -\frac{1}{3}\, &{} \quad -\frac{1}{3}\, &{}\quad \frac{2}{3}\, &{}\quad 0\, &{}\quad 0\, &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 2 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 2 &{} \quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 2 \\ \end{array} } \right] \end{aligned}$$

(66)

Employing, $\mathbf {M}$, $\mathbf{C}$ is written as:

$$\begin{aligned} \begin{aligned} \mathbf{C}=\gamma \left\langle F \right\rangle ^{q} \left[ \frac{\sqrt{3}}{2 \bar{{\sigma }}} \mathbf{M} + \left( \frac{q \left[ \text {sign}(F) +1\right] }{2 \left\langle f \right\rangle }-\frac{\sqrt{3}}{3 \bar{{\sigma }}} \right) \mathbf{a} \otimes \mathbf{a}\right] \end{aligned} \end{aligned}$$

(67)

Using Eq. (63):

$$\begin{aligned} \mathbf{G} = \frac{\partial \dot{\varvec{\varepsilon }}^{vp}}{\partial \varvec{\varepsilon }^{vp} }=\frac{\gamma ~q}{2}\left\langle F \right\rangle ^{q-1}\left[ \text {sign}(F)+1\right] ~\frac{\partial F}{\partial \varvec{\varepsilon }^{vp}} \otimes \mathbf{a} \end{aligned}$$

(68)

Employing chain rule, we obtain:

$$\begin{aligned} \frac{\partial F}{\partial \varvec{\varepsilon }^{vp} }= & {} \frac{\partial f}{\partial \bar{\varepsilon }^{vp}}~\frac{\partial \bar{\varepsilon }^{vp}}{\partial \varvec{\varepsilon }^{vp}}~\frac{1}{{\sigma }_{y}} -\frac{f}{{\sigma _y}^{2}}~\frac{\partial \sigma _y}{\partial \bar{\varepsilon }^{vp}}~\frac{\partial \bar{\varepsilon }^{vp}}{\partial \varvec{\varepsilon }^{vp}}\nonumber \\= & {} -\frac{2}{3} B n (\bar{\varepsilon }^{vp})^{n-2} ~ \left( \frac{\sigma _y + f}{{\sigma _y}^2}\right) ~ {\varvec{\varepsilon }}^{vp} \end{aligned}$$

(69)

Therefore,

$$\begin{aligned} \begin{aligned} \mathbf{G}&= - [\text {sign}(F)+1] \left( \frac{\gamma ~q~B~n}{3}\right) \left\langle F \right\rangle ^{q-1}~ (\bar{\varepsilon }^{vp})^{n-2}\\&\quad \; \times \left( \frac{\sqrt{3} \bar{\sigma }}{{\sigma _y}^2}\right) {\varvec{\varepsilon }}^{vp} \otimes \mathbf{a} \end{aligned} \end{aligned}$$

(70)