Skip to main content
SpringerLink
Log in

Random homogenization analysis for heterogeneous materials with full randomness and correlation in microstructure based on finite element method and Monte-carlo method

  • Original Paper
  • Published:
Computational Mechanics Aims and scope Submit manuscript

Abstract

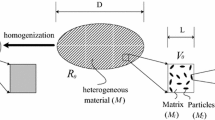
The computationally random homogenization analysis of a two-phase heterogeneous materials is addressed in the context of linear elasticity where the randomness of constituents’ moduli and microstructural morphology together with the correlation among random moduli are fully considered, and random effective quantities such as effective elastic tensor and effective stress as well as effective strain energy together with their numerical characteristics are then sought for different boundary conditions. Based on the finite element method and Monte-carlo method, the RVE with randomly distributing particles determined by a numerical convergence scheme is firstly generated and meshed, and two types of boundary conditions controlled by average strain are then applied to the RVE where the uncertainty existing in the microstructure is accounted for simultaneously. The numerical characteristics of random effective quantities such as coefficients of variation and correlation coefficients are then evaluated, and impacts of different factors on random effective quantities are finally investigated and revealed as well.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22

Similar content being viewed by others

References

  1. Forest S, Barbe F, Cailletaud G (2007) Cosserat modelling of size effects in the mechanical behavior of polycrystals and multi-phase materials. Int. J. Solids Struct. 37:7105–7126

    Article  MathSciNet  Google Scholar 

  2. Ghosh S, Lee K, Raghavan P (2001) A multi-level computational model for multi-scale damage analysis in composite and porous materials. Int J Solids Struct 38:2335–2385

    Article  MATH  Google Scholar 

  3. Bonnet C (2007) Effective properies of elastic periodic composite media with fibers. J Mech Phys Solids 55(5):881–899

    Article  MATH  MathSciNet  Google Scholar 

  4. Hill R, Rice JR (1973) Elastic potentials and the structure of inelastic constitutive laws. SIAM J Appl Math 25(3):448–461

    Article  MATH  MathSciNet  Google Scholar 

  5. Huet C (1990) Application of variational concepts to size effects in elastic heterogeneous bodies. J Mech Phys Solids 38(6):813–841

    Article  MathSciNet  Google Scholar 

  6. Terada K, Hori M, Kyoya T, Kikuchi N (2000) Simulation of the multi-scale convergence in computational homogenization approach. Int J Solids Struct 37:2285–2311

    Article  MATH  Google Scholar 

  7. Aboudi J (1991) Mechanics of composite materials: a unified micromechanical approach. Elsevier, Amsterdam

    MATH  Google Scholar 

  8. Christensen RM (1991) Mechanics of composite materials. Krieger, New York

    Google Scholar 

  9. Cioranescu D, Donato P (1998) An introduction to homogenization. Oxford University Press, New York

    Google Scholar 

  10. Mura T (1987) Micromechanics of defects in solids. Martinus Nijhoff, The Hague

    Book  Google Scholar 

  11. Nemat-Nasser S, Hori M (1999) Micromechanics: overall properties of heterogeneous materials, 2nd edn. North-Holland, Amsterdam

    Google Scholar 

  12. Torquato S (2002) Random heterogeneous materials: microstructure and macroscopic properties. Springer, Berlin Heidelberg New York

    Book  Google Scholar 

  13. Zohdi TI, Wriggers P (2005) Introduction to computational micromechanics. Springer, Berlin Heidelberg New York

    Book  MATH  Google Scholar 

  14. Kanit T, Forest S, Galliet I, Mounoury V, Jeulin D (2003) Determination of the size of the representative volume element for random composites: statistical and numerical approach. Int J Solids Struct 40:3647–3679

    Article  MATH  Google Scholar 

  15. Forest S, Pradel F, Sab K (2001) Asymptotic analysis of heterogeneous Cosserat media. Int J Solids Struct 38:4585–4608

    Article  MATH  MathSciNet  Google Scholar 

  16. Mindlin RD (1965) Second gradient of strain and surface-tension in linear elasticity. Int J Solids Struct 1:417–438

    Article  Google Scholar 

  17. Ghosh Somnath, Lee Kyunghoon, Moorthy Suresh (1995) Multiple scale analysis of heterogeneous elastic structures using homogenization theory and voronoi cell finite element method. Int J Solids Struct 32(1):27–62

    Article  MATH  MathSciNet  Google Scholar 

  18. Stroeven M, Askes H, Sluys LJ (2004) Numerical determination of representative volumes for granular materials. Comput Methods Appl Mech Eng 193:3221–3238

    Article  MATH  Google Scholar 

  19. Matthies Hermann G (2008) Stochastic finite elements: computational approaches to stochastic partial differential equations. ZAMM J Appl Math Mech 88(11):849–873

    Article  MATH  MathSciNet  Google Scholar 

  20. Ma J, Temizer I, Wriggers P (2011) Uncertain analysis of the homogenization in the heterogeneous material of linear elasticity. Int J Solids Struct 48:280–291

    Article  MATH  Google Scholar 

  21. Kucerova A, Matthies HG (2010) Uncertainty updating in the description of heterogeneous materials. Technische Mechanik 30(1–3):211–226

    Google Scholar 

  22. Matthies HG, Zander E (2012) Solving stochastic systems with low-rank tensor compression. Linear Algebra Appl 436(10):3819–3838

    Article  MATH  MathSciNet  Google Scholar 

  23. Hall RA (1991) Computer modeling of rubber-toughened plastics: random placement of monosized core-shell particles in a polymer matrix and interparticle distance calculations. J Mater Sci 26:5631–5636

    Article  Google Scholar 

  24. Sakata S, Ashida F, Kojima T, Zako M (2008) Three-dimensional stochastic analysis using a perturbationbased homogenization method for elastic properties of composite material considering microscopic uncertainty. Int J Solids Struct 45:894–907

    Article  MATH  Google Scholar 

  25. Kari S, Berger H, Gabbert U (2007) Numerical evaluation of effective material properties of randomly distributed short cylindrical fibre composites. Comp Mater Sci 39(1):198–204

    Article  Google Scholar 

  26. Trias D, costa J, Mayugo JA, Hurtado JE (2006) Random models versus periodic models for fibre reinforced composites. Comp Mater Sci 38(2):316–324

    Article  Google Scholar 

  27. Xu XF, Graham-Brady L (2005) A stochastic computational method for evaluation of global and local behavior of random elastic media. Comput Methods Appl Mech Eng 194(42–44):4362–4385

    Article  MATH  Google Scholar 

  28. Caffarelli LA, Mellet A (2009) Random homogenization of an obstacle problem. A\(^{.}\)nnales de l’Institut Henri Poincare (C) Non Linear Analysis 26(2):375–395

  29. Kari S, Berger H, Rodriguez-Ramos R, Gabbert U (2007) Computational evaluation of effective material properties of composites reinforced by randomly distributed spherical particles. Compos Struct 77(2):223–231

    Article  Google Scholar 

  30. Frank Xu X, Chen Xi (2009) Stochastic homogenization of random elastic multi-phase composites and size quantification of representative volume element. Mech Mater 41(2):174–186

    Article  Google Scholar 

  31. Ostoja-Starzewski M (1998) Random field models of heterogeneous materials. Int J Solids Struct 35(19):2429–2455

    Article  MATH  Google Scholar 

  32. Pelissou C, Baccou J, Monerie Y, Perales F (2009) Determination of thesize of the representative volume element for random quasi-brittle composites. Int J solids Struct 46(14–15):2842–2855

  33. Kanit T, Forest S, Galliet I, Mounoury V, Jeulin D (2003) Determination of the size of the representative volume element for random composites: statistical and numerical approach. Int J Solids Struct 40:3647–3679

    Article  MATH  Google Scholar 

  34. Sab K (1992) On the homogenization and the simulation of random matrials. Eur J Mech Solids 11:585–607

    MATH  MathSciNet  Google Scholar 

  35. Chen Zhangxin, Savchuk Tatyana Y (2008) Analysis of the multiscale finite element method for nonlinear and random homogenization problems. SIAM J Numer Anal 46(1):260–279

    Article  MATH  MathSciNet  Google Scholar 

  36. Bal Guillaume, Jing Wenjia (2011) Corrector theory for MsFEM and HMM in random media. Multiscale Model Simul 9(4):1549–1587

    Article  MATH  MathSciNet  Google Scholar 

  37. Cluni F, Gusella V (2013) Homogenization of non-periodic masonry structures. Int J Solids Struct Available online: http://dx.doi.org/10.1016/j.ijsolstr.2003.11.011

  38. Kamiński Marcin (2009) Sensitivity and randomness in homogenization of periodic fiber-reinforced composites via the response function method. Int J Solids Struct 46:923–937

    Article  MATH  Google Scholar 

  39. Kamiński Marcin (2012) Probabilistic entropy in homogenization of the periodic fiber-reinforced composites with random elastic parameters. Int J Numer Methods Eng 90(8):939–954

    MATH  Google Scholar 

  40. Jia X, Williams RA (2001) A packing algorithm for particles of arbitrary shapes. Powder Technol 120:175–186

    Article  Google Scholar 

  41. Hill R (1963) Elastic properties of reinforced solids: some theoretical principles. J Mech Phys Solids 11:357–372

    Article  MATH  Google Scholar 

  42. Touran A, Wiser EP (1992) Monte Carlo technique with correlated random variables. J Construct Eng Manag 118:258–272

    Article  Google Scholar 

  43. Temizer I, Zohdi TI (2007) A numerical method for homogenization in non-linear elasticity. Comp Mech 40:281–298

    Article  MATH  Google Scholar 

  44. Hazanov S, Huet C (1994) Order relationships for boundary conditions effect in heterogeneous bodies smaller than the representative volume. J Mech Phys Solids 42(12):1995–2011

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

The first author gratefully acknowledges the support of the Alexander von Humboldt Stiftung through a ‘Humboldt Research Fellowship for Postdoctoral Researchers’ for a research stay at the Leibniz Universität Hannover. The support of Natural Science Foundation of China to the project (JJ0500110405) “Random homogenization of heterogeneous materials with infinitesimal and finite deformation” is also gratefully acknowledged.

Author information

Authors and Affiliations

  1. Key Laboratory of Electronic Equipment Structure Design, Ministry of Education, Xidian University, P.O.Box: 187, Xi’an , 710071, People’s Republic of China

    Juan Ma, Jie Zhang & Liangjie Li

  2. Institute of Continuum Mechanics, Leibniz Universität Hannover, 30167 , Hannover, Germany

    Peter Wriggers & Shahab Sahraee

Authors
  1. Juan Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jie Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Liangjie Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Peter Wriggers
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Shahab Sahraee
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Juan Ma.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ma, J., Zhang, J., Li, L. et al. Random homogenization analysis for heterogeneous materials with full randomness and correlation in microstructure based on finite element method and Monte-carlo method. Comput Mech 54, 1395–1414 (2014). https://doi.org/10.1007/s00466-014-1065-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00466-014-1065-6

Keywords

Search

Navigation