1 Introduction

Consider a family \({\mathcal {K}}\) of positive homothetic copies of a fixed convex body \(K \subset {\mathbb {R}}^d\) with homothety coefficients \(\tau _1, \ldots , \tau _n > 0\). Following Hadwiger [6], we call \({\mathcal {K}}\) non-separable if any hyperplane H intersecting \({{\mathrm{conv}}}\bigcup {\mathcal {K}}\) intersects a member of \({\mathcal {K}}\). Answering a question by Erdős, A.W. Goodman and R.E. Goodman [4] proved the following assertion:

Theorem 1.1

(A.W. Goodman, R.E. Goodman, 1945) Given a non-separable family \({\mathcal {K}}\) of Euclidean balls of radii \(r_1, \ldots , r_n\) in \({\mathbb {R}}^d\), it is always possible to cover them by a ball of radius \(R = \sum r_i\).

Let us outline here the idea of their proof since we are going to reuse it in different settings.

First, A.W. Goodman and R.E. Goodman prove the following lemma, resembling the 1-dimensional case of the general theorem:

Lemma 1.2

Let \(I_1, \ldots , I_n \subset {\mathbb {R}}\) be segments of lengths \(\ell _1, \ldots , \ell _n\) with midpoints \(c_1, \ldots , c_n\). Assume the union \(\bigcup I_i\) is a segment (i.e. the family of segments is non-separable). Then the segment I of length \(\sum \ell _i\) with midpoint at the center of mass \(c = \frac{\sum \ell _i c_i}{\sum \ell _i}\) covers \(\bigcup I_i\).

Next, for a family \({\mathcal {K}} = \{o_i + r_i B\}\) (B denotes the unit ball centered at the origin of \({\mathbb {R}}^d\)), A.W. Goodman and R.E. Goodman consider the point \(o = \frac{\sum r_i o_i}{\sum r_i}\) (i.e., the center of mass of \({\mathcal {K}}\) if the weights of the balls are chosen to be proportional to the radii). They project the whole family onto d orthogonal directions (chosen arbitrarily) and apply Lemma 1.2 to show that the ball of radius \(R = \sum r_i\) centered at o indeed covers \({\mathcal {K}}\).

In [2], K. Bezdek and Z. Lángi show that Theorem 1.1 actually holds not only for balls but also for any centrally-symmetric bodies:

Theorem 1.3

(K. Bezdek and Z. Lángi, 2016) Given a non-separable family of homothets of centrally-symmetric convex body \(K \subset {\mathbb {R}}^d\) with homothety coefficients \(\tau _1, \ldots , \tau _n > 0\), it is always possible to cover them by a translate of \(\big (\sum \tau _i\big )K\).

The idea of their proof is to use Lemma 1.2 to deduce the statement for the case when K is a hypercube, and then deduce the result for sections of the hypercube (which can approximate arbitrary centrally-symmetric bodies).

It is worth noticing that Theorem 1.3 follows from Lemma 1.2 by a more direct argument (however, missed by A.W. Goodman and R.E. Goodman). In 2001, F. Petrov proposed a particular case of the problem (when K is a Euclidean ball) to Open Mathematical Contest of Saint Petersburg Lyceum  239 [1]. He assumed the following solution (working for any symmetric K as well): For a family \({\mathcal {K}} = \{o_i + \tau _i K\}\), consider a homothet \(\big (\sum \tau _i\big ) K + o\) with center \(o = \frac{\sum \tau _i o_i}{\sum \tau _i}\). If \(\big (\sum \tau _i\big ) K + o\) does not cover \({\mathcal {K}}\), then there exists a hyperplane H separating a point \(p \in {{\mathrm{conv}}}\bigcup {\mathcal {K}} \setminus \big (\big (\sum \tau _i\big ) K + o\big )\) from \(\big (\big (\sum \tau _i\big ) K + o\big )\). Projection onto the direction orthogonal to H reveals a contradiction with Lemma 1.2.

Another interesting approach to Goodmans’ theorem was introduced by K. Bezdek and A. Litvak [3]. They put the problem in the context of studying the packing analogue of Bang’s problem through the LP-duality, which gives yet another proof of Goodmans’ theorem for the case when K is a Euclidean disk in the plane. One can adapt their argument for the original Bang’s problem to get a “dual” counterpart of Goodmans’ theorem. We discuss this counterpart and give our proof of a slightly more general statement in Sect. 4.

The paper is organized as follows. In Sect. 2 we prove a strengthening (with factor \(\frac{d+1}{2}\) instead of d) of the following result of K. Bezdek and Z. Lángi:

Theorem 1.4

(K. Bezdek and Z. Lángi, 2016) Given a non-separable family of positive homothetic copies of a (not necessarily centrally-symmetric) convex body \(K \subset {\mathbb {R}}^d\) with homothety coefficients \(\tau _1, \ldots , \tau _n > 0\), it is always possible to cover them by a translate of \(d\big (\sum \tau _i\big )K\).

In Sect. 3 we show that if we weaken the condition of non-separability considering only \(d+1\) directions of separating hyperplanes, then the factor \(\frac{d+1}{2}\) cannot be improved.

In Sect. 4 we prove a counterpart of Goodmans’ theorem related to the notion somehow opposite to non-separability: Given a positive integer k and a family of Euclidean balls of radii \(r_1, \ldots , r_n\) in \({\mathbb {R}}^d\), it is always possible to inscribe a ball of radius \(r =\frac{1}{2} \big (\sum r_i\big )\) within their convex hull, provided every hyperplane intersects at most k interiors of the balls.

2 A Goodmans-Type Result for Non-symmetric Bodies

Let \(K \subset {\mathbb {R}}^d\) be a (not necessarily centrally-symmetric) convex body containing the origin and let \(K^\circ = \{p : \langle p,q \rangle \le 1 \text { for all } q \in K\}\) (where \(\langle \cdot ,\cdot \rangle \) stands for the standard inner product) be its polar body. We define the following parameter of asymmetry:

$$\begin{aligned} \sigma = \min \limits _{q\in {{\mathrm{int}}}K} \min {\{\mu >0: (K-q) \subset -\mu (K-q)\}}. \end{aligned}$$

It is an easy exercise in convexity to establish that \(\min \{\mu>0: (K-q) \subset -\mu (K-q)\} = \min {\{\mu >0: (K-q)^\circ \subset -\mu (K-q)^\circ \}}\). So an equivalent definition (which is more convenient for our purposes) is

$$\begin{aligned} \sigma = \min \limits _{q\in {{\mathrm{int}}}K} \min {\{\mu >0: (K-q)^\circ \subset -\mu (K-q)^\circ \}}. \end{aligned}$$

The value \(\frac{1}{\sigma }\) is often referred to as Minkowski’s measure of symmetry of body K (see, e.g., [5]).

Theorem 2.1

Given a non-separable family of positive homothetic copies of (not necessarily centrally-symmetric) convex body \(K \subset {\mathbb {R}}^d\) with homothety coefficients \(\tau _1, \ldots , \tau _n > 0\), it is always possible to cover them by a translate of \(\frac{\sigma +1}{2}\big (\sum \tau _i\big )K\). (Here \(\sigma \) denotes the parameter of asymmetry of K, defined above.)

Proof

We start by shifting the origin so that \(K^\circ \subset -\sigma K^\circ \).

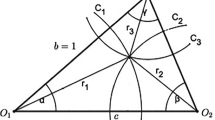
For a family \({\mathcal {K}} = \{o_i + \tau _i K\}\), consider the homothet \(\frac{\sigma +1}{2} \big (\sum \tau _i\big ) K + o\) with center \(o = \frac{\sum \tau _i o_i}{\sum \tau _i}\). Assume that \(\frac{\sigma +1}{2}\big (\sum \tau _i\big ) K + o\) does not cover \({\mathcal {K}}\), hence there exists a hyperplane H (strictly) separating a point \(p \in {{\mathrm{conv}}}\bigcup {\mathcal {K}} \setminus \big (\frac{\sigma +1}{2}\big (\sum \tau _i\big ) K + o\big )\) from \(\big (\frac{\sigma +1}{2}\big (\sum \tau _i\big ) K + o\big )\). Consider the orthogonal projection \(\pi \) along H onto the direction orthogonal to H. Suppose the segment \(\pi (K)\) is divided by the projection of the origin in the ratio 1 : s. Since \(K^\circ \subset -\sigma K^\circ \), we may assume that \(s \in [1, \sigma ]\). Identify the image of \(\pi \) with the coordinate line \({\mathbb {R}}\) and denote \(I_i = [a_i, b_i] = \pi \big (o_i + \tau _i K\big )\), \(c_i = \pi (o_i)\), \(\ell _i = b_i - a_i\), \(L = \sum \ell _i\) (see Fig. 1). Note that the \(\ell _i\) are proportional to the \(\tau _i\), and that \(s(c_i - a_i) = b_i - c_i\). Denote \(c = \pi (o) = \frac{\sum \ell _i c_i}{L}\) and \(I = [a,b] = \pi \big (\frac{\sigma +1}{2}\big (\sum \tau _i\big ) K + o\big )\) the segment of length \(\frac{\sigma +1}{2}L\) divided by c in the ratio 1 : s.

Fig. 1
figure 1

Illustration of the proof of Theorem 2.1

Full size image

Also consider the midpoints \(c_i' = \frac{a_i+b_i}{2}\). By Lemma 1.2, the segment \(I' = [a',b']\) of length L with midpoint at \(c' = \frac{\sum \ell _i c_i'}{L}\) covers the union \(\bigcup I_i =\pi ({\mathcal {K}})\). Let us check that \(I' \subset I\), which would be a contradiction, since \(\pi (p) \in I'\), \(\pi (p) \notin I\).

First, notice that

$$\begin{aligned} c_i' = \frac{a_i + b_i}{2} \ge \frac{s a_i + b_i}{1+s} = c_i, \end{aligned}$$

hence

$$\begin{aligned} a' = c' - \frac{1}{2} \,L \ge c - \frac{1}{2}\, L \ge c - \frac{1}{1+s} \,\frac{\sigma +1}{2} \,L = a. \end{aligned}$$

Second,

$$\begin{aligned} c_i' - c_i = \frac{a_i+b_i}{2} - \frac{sa_i + b_i}{1+s} = \frac{s-1}{s+1}\, \frac{\ell _i}{2}, \end{aligned}$$

hence

$$\begin{aligned} b'= & {} c' + \frac{1}{2}\, L = c + (c'-c) + \frac{1}{2}\, L = c + \frac{s-1}{2(s+1)} \,\frac{\sum \ell _i^2}{L} + \frac{1}{2} \,L\\\le & {} c + \frac{s-1}{2(s+1)} \,L + \frac{1}{2}\, L \le c + \frac{s}{1+s}\, \frac{\sigma +1}{2}\, L = b. \end{aligned}$$

\(\square \)

Lemma 2.2

(H. Minkowski and J. Radon) Let K be a convex body in \({\mathbb {R}}^d\). Then \(\sigma \le d\), where \(\sigma \) denotes the parameter of asymmetry of K, defined above.

For the sake of completeness we provide a proof here.

Proof

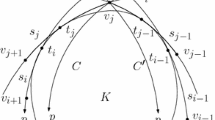
Suppose the origin coincides with the center of mass \(g = \int _K x \, dx / \int _K dx\). We show that \(K^\circ \subset -d K^\circ \). Consider two parallel support hyperplanes orthogonal to one of the coordinate axes \(Ox_1\). We use the notation \(H_t = \{x = (x_1,\ldots ,x_d): x_1 = t\}\) for hypeplanes orthogonal to this axis. Without loss of generality, these support hyperplanes are \(H_{-1}\) and \(H_s\) for some \(s \ge 1\). We need to prove \(s \le d\).

Assume that \(s > d\). Consider a cone C defined as follows: its vertex is chosen arbitrarily from \(K \cap H_s\); its section \(C \cap H_0 = K \cap H_0\); the cone is truncated by \(H_{-1}\). Since C is a d-dimensional cone, the \(x_1\)-coordinate of its center of mass divides the segment \([-1, s]\) in ratio 1 : d. Therefore, the center of mass has positive \(x_1\)-coordinate. It follows from convexity of K that \(C \setminus K\) lies (non-strictly) between \(H_{-1}\) and \(H_0\), hence the center of mass of \(C \setminus K\) has non-positive \(x_1\)-coordinate. Similarly, \(K \setminus C\) lies (non-strictly) between \(H_0\) and \(H_s\), hence its center of mass has non-negative \(x_1\)-coordinate. Thus, the center of mass of \(K = (C \setminus (C \setminus K)) \cup (K \setminus C)\) (see Fig. 2) must have positive \(x_1\)-coordinate, which is a contradiction. \(\square \)

Fig. 2
figure 2

Illustration of the proof of Lemma 2.2

Full size image

Corollary 2.3

The factor d in Theorem 1.4 can be improved to \(\frac{d+1}{2}\).

Proof

The result follows from Theorem 2.1 and Lemma 2.2.

An alternative proof of this corollary that avoids Lemma 2.2 is as follows. We use the notation of Theorem 1.4. Consider the smallest homothet \(\tau K\), \(\tau > 0\), that can cover \({\mathcal {K}}\) (after a translation to \(\tau K + t\), \(t \in {\mathbb {R}}^d\)). Since it is the smallest, its boundary touches \(\partial {{\mathrm{conv}}}\bigcup {\mathcal {K}}\) at some points \(q_0\), \(\ldots \), \(q_m\) (\(m \le d\)) such that the corresponding support hyperplanes \(H_0\), \(\ldots \), \(H_m\) bound a nearly bounded set S, i.e., a set that can be placed between two parallel hyperplanes.

Circumscribe all the bodies from the family \({\mathcal {K}}\) by the smallest homothets of S and apply Theorem 2.1 for them (note that if \(m<d\) then S is unbounded, but that does not ruin our argument). Since S is a cylinder based on an m-dimensional simplex, its parameter of asymmetry equals \(m \le d\), and we are done. \(\square \)

Remark 2.4

Up to this moment the best possible factor for non-symmetric case is unknown. Bezdek and Lángi [2] give a sequence of examples in \({\mathbb {R}}^d\) showing that it is impossible to obtain a factor less than \(\frac{2}{3} + \frac{2}{3\sqrt{3}}\) \((> 1)\) for any \(d \ge 2\).

3 A Sharp Goodmans-Type Result for Simplices

Consider the case when \(K \subset {\mathbb {R}}^d\) is a simplex. In this section we are only interested in separating hyperplanes parallel to a facet of K.

Theorem 3.1

Let \({\mathcal {K}}\) be a family of positive homothetic copies of a simplex \(K \subset {\mathbb {R}}^d\) with homothety coefficients \(\tau _1,\ldots ,\tau _n > 0\). Suppose any hyperplane H (parallel to a facet of K) intersecting \({{\mathrm{conv}}}\bigcup {\mathcal {K}}\) intersects a member of \({\mathcal {K}}\). Then it is possible to cover \(\bigcup {\mathcal {K}}\) by a translate of \(\frac{d+1}{2}\big (\sum \tau _i\big )K\). Moreover, the factor \(\frac{d+1}{2}\) cannot be improved.

Proof

A proof of possibility to cover follows the same lines as (and is even simpler than) the proof of Theorem 2.1. Let K have its center of mass at the origin. For a family \({\mathcal {K}} = \{o_i + \tau _i K\}\), consider a homothet \(\frac{d+1}{2} \big (\sum \tau _i\big ) K + o\) with center \(o = \frac{\sum \tau _i o_i}{\sum \tau _i}\). Assuming \(\frac{d+1}{2}\big (\sum \tau _i\big ) K + o\) does not cover \({\mathcal {K}}\), we find a hyperplane H (strictly) separating a point \(p \in {{\mathrm{conv}}}\bigcup {\mathcal {K}} \setminus \big (\frac{d+1}{2}\big (\sum \tau _i\big ) K + o\big )\) from \(\big (\frac{d+1}{2}\big (\sum \tau _i\big ) K + o\big )\). Note that H can be chosen among the hyperplanes spanned by the facets of \(\big (\frac{d+1}{2}\big (\sum \tau _i\big ) K + o\big )\), so H is parallel to one of them.

After projecting everything along H onto the direction orthogonal to H, we repeat the same argument as before and show that (in the notation from Theorem 2.1)

$$\begin{aligned} a' = c' - \frac{1}{2} \,L \ge c - \frac{1}{2}\, L = a, \end{aligned}$$

which contradicts our assumption.

Next, we construct an example showing that the factor \(\frac{d+1}{2}\) cannot be improved.

Consider a simplex

$$\begin{aligned} K = \biggl \{x = (x_1, \ldots , x_d) \in {\mathbb {R}}^d: x_i \ge 0,\, \sum \limits _{i=1}^d x_i \le \frac{d(d+1)}{2}\, N + 1\biggr \}, \end{aligned}$$

where N is an arbitrary large integer. Section it with all hyperplanes of the form \(\{x_i = t\}\) or of the form \(\sum \nolimits _{i=1}^d x_i = t\) (for \(t \in \mathbb {Z}\)). Consider all the smallest simplices generated by these cuts and positively homothetic to K. We use coordinates

$$\begin{aligned} \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix}, \quad 0 \le b_i \in \mathbb {Z}, \quad \sum \limits _{i=1}^d b_i \le \frac{d(d+1)}{2}\, N, \end{aligned}$$

to denote the simplex lying in the hypercube \(\{b_i \le x_i \le b_i+1, i = 1, \ldots , d\}\).

For \(d=2\) (see Fig. 3) we compose \({\mathcal {K}}\) of the simplices with the following coordinates:

$$\begin{aligned} \begin{pmatrix} 0 \\ N \end{pmatrix}, \begin{pmatrix} 1 \\ N+1 \end{pmatrix}, \ldots , \begin{pmatrix} N \\ 2N \end{pmatrix}, \begin{pmatrix} N+1 \\ 0 \end{pmatrix}, \ldots , \begin{pmatrix} 2N \\ N-1 \end{pmatrix}. \end{aligned}$$
Fig. 3
figure 3

Example for \(d=2\) and \(N=5\)

Full size image

For \(d=3\):

$$\begin{aligned} \begin{pmatrix} 0 \\ N \\ 2N \end{pmatrix}, \begin{pmatrix} 1 \\ N+1 \\ 2N+1 \end{pmatrix}, \ldots , \begin{pmatrix} N \\ 2N \\ 3N \end{pmatrix}, \begin{pmatrix} N+1 \\ 2N+1 \\ 0 \end{pmatrix}, \ldots , \begin{pmatrix} 2N \\ 3N \\ N-1 \end{pmatrix}, \begin{pmatrix} 2N+1 \\ 0 \\ N \end{pmatrix}, \ldots , \begin{pmatrix} 3N \\ N-1 \\ 2N-1 \end{pmatrix}. \end{aligned}$$

For general d:

$$\begin{aligned} \begin{pmatrix} 0 \\ N \\ 2N \\ \vdots \\ (d-1)N \end{pmatrix}, \begin{pmatrix} 1 \\ N+1 \\ 2N+1 \\ \vdots \\ (d-1)N+1 \end{pmatrix}, \ldots , \begin{pmatrix} i \pmod {dN+1} \\ N + i \pmod {dN+1}\\ 2N + i \pmod {dN+1}\\ \vdots \\ (d-1)N + i \pmod {dN+1} \end{pmatrix}, \ldots , \begin{pmatrix} dN \\ N-1 \\ 2N-1 \\ \vdots \\ (d-1)N-1 \end{pmatrix}. \end{aligned}$$

It is rather straightforward to check that each \(b_i\) ranges over the set \(\{0, 1, \ldots , dN\}\), and their sum is not greater than \(\frac{d(d+1)}{2} N\). Therefore, the chosen family \({\mathcal {K}}\) is indeed non-separable by hyperplanes parallel to the facets of K. Moreover, the chosen simplices touch all the facets of K, so K is the smallest simplex covering \({\mathcal {K}}\). Finally, we note that any one-dimensional parameter of K (say, its diameter) is \(\frac{{d(d+1)} N}{{2}(dN+1)}\) times greater than the sum of the corresponding parameters of the elements of \({\mathcal {K}}\), and this ratio tends to \(\frac{d+1}{2}\) as \(N \rightarrow \infty \). \(\square \)

4 A “Dual” Version of Goodmans’ Theorem

Lemma 4.1

Let \(I_1, \ldots , I_n \subset {\mathbb {R}}\) be segments of lengths \(\ell _1, \ldots , \ell _n\) with midpoints \(c_1, \ldots , c_n\). Assume every point on the line belongs to at most k of the interiors of the \(I_i\). Then the segment I of length \(\frac{1}{k}\sum \ell _i\) with midpoint at the center of mass \(c = \frac{\sum \ell _i c_i}{\sum \ell _i}\) lies in \({{\mathrm{conv}}}\bigcup I_i\).

Proof

Mark all the segment endpoints and subdivide all the segments by the marked points. Next, put the origin at the leftmost marked point and numerate the segments between the marked points from left to right. We say that the i-th segment is of multiplicity \(0 \le k_i \le k\) if it is covered \(k_i\) times. We keep the notation \(I_i\) for the new segments with multiplicities, \(c_i\) for their midpoints, and \(\ell _i\) for their lengths. Note that the value \(\frac{\sum \ell _i c_i}{\sum \ell _i}\) is preserved after this change of notation: it is the coordinate of the center of mass of the segments regarded as solid one-dimensional bodies of uniform density.

Note that \(c_i = \ell _1 + \cdots + \ell _{i-1} + \frac{1}{2} \ell _i\). We prove that

$$\begin{aligned} c = \frac{\sum k_i\ell _i c_i}{\sum k_i\ell _i} \ge \frac{\sum k_i \ell _i}{2k} \end{aligned}$$

(this would mean that the left endpoint of I is contained in \({{\mathrm{conv}}}\bigcup I_i\); for the right endpoint everything is similar).

The inequality in question

$$\begin{aligned} 2c \sum _i k_i \ell _i&= k_1 \ell _1 \cdot \ell _1 + k_2 \ell _2 \cdot (2\ell _1 + \ell _2) + k_2 \ell _2 \cdot (2\ell _1 + 2\ell _2 + \ell _3) + \cdots \\&\mathop {\ge }\limits ^{?}\frac{1}{k} \Big ( \sum _i k_i\ell _i \Big )^{2} \end{aligned}$$

is equivalent to

$$\begin{aligned} k \biggl ( \sum _i k_i\ell _i^2 + 2 \sum _{i<j} k_j\ell _i\ell _j \biggr )\mathop {\ge }\limits ^{?}\biggl ( \sum _i k_i\ell _i \biggr )^{2}, \end{aligned}$$

which is true, since \(k \ge k_i\). \(\square \)

Theorem 4.2

Let k be a positive integer, and \({\mathcal {K}}\) be a family of positive homothetic copies (with homothety coefficients \(\tau _1, \ldots , \tau _n > 0\)) of a centrally-symmetric convex body \(K \subset {\mathbb {R}}^d\). Suppose any hyperplane intersects at most k interiors of the homothets. Then it is possible to put a translate of \(\frac{1}{k}\big (\sum \tau _i\big ) K\) into their convex hull.

Proof

As usual, for a family \({\mathcal {K}} = \{o_i + \tau _i K\}\), consider a homothet \(\frac{1}{k}\big (\sum \tau _i\big ) K + o\) with center \(o = \frac{\sum \tau _i o_i}{\sum \tau _i}\). Assume \(\frac{1}{k} \big (\sum \tau _i\big ) K + o\) does not fit into \({{\mathrm{conv}}}\bigcup {\mathcal {K}}\), then there exists a hyperplane H separating a point \(p \in \frac{1}{k} \big (\sum \tau _i\big ) K + o\) from \({{\mathrm{conv}}}\bigcup {\mathcal {K}}\). After projecting onto the direction orthogonal to H, we use Lemma 4.1 to obtain a contradiction.\(\square \)

Remark 4.3

The estimate in Theorem 4.2 is sharp for any k, as can be seen from the example of k translates of K lying along the line so that consecutive translates touch.