A Question from a Famous Paper of Erdős

Abstract

Given a convex body $K$, consider the smallest number $N$ so that there is a point $P\in \partial K$ such that every circle centred at $P$ intersects $\partial K$ in at most $N$ points. In 1946 Erdős conjectured that $N=2$ for all $K$, but there are convex bodies for which this is not the case. As far as we know there is no known global upper bound. We show that no convex body has $N=\infty$ and that there are convex bodies for which $N = 6$.

1 Introduction

Paul Erdős often said that his most important contribution to discrete geometry was his paper [1] from 1946 entitled “On sets of distances of $n$ points”. In this short and very influential paper, with more than 300 citations according to Google Scholar, Erdős writes:

“On every convex curve there exists a point $P$ such that every circle with centre $P$ intersects the curve in at most $2$ points.”

This statement is easily shown to be false; for any point $P$ on the boundary of an acute triangle there is a circle centred at $P$ that intersects the boundary of the triangle $4$ times. In fact, any regular $(2k+1)$-gon has this property.

It might be possible that the number 2 in this conjecture can be replaced by some other number independent of the convex curve. We wish to determine how large this number can be.

A related conjecture, also by Erdős, was that every convex polygon has a vertex $P$ such that no three other vertices are equidistant from it. This was disproved by Danzer [2] and (in a stronger form) by Fishburn and Reeds [4].

Let $K$ be a planar convex body. We define $N=N(K)\in \mathbb N \cup \{\infty \}$ as the smallest number for which there is a point $P\in \partial K$ such that every circle with centre $P$ intersects $\partial K$ in at most $N$ points. With this notation, Erdős’s original conjecture states that $N(K)\le 2$ for every convex body $K$. We conjecture that $N(K)$ is indeed bounded by some finite constant independent of $K$, probably by $6$.

Theorem 1.1

There is a planar convex body $K$ with $N(K)=6$.

In Sect. 3 we construct a 15-gon with this property. This is the simplest example we have found so far. On the other hand we can prove the following theorem.

Theorem 1.2

For every planar convex body $K, N(K)<\infty$.

A stronger version of this theorem is proved in Sect. 2. So far we have not been able to find a finite upper bound that works for all $K$. Part of the difficulty of improving this bound may come from the following two theorems.

For $n\in \mathbb N \cup \{\infty \}$, let $J(K,n)$ be the set of points $P\in \partial K$ such that there is a circle centred at $P$ that intersects $\partial K$ in at least $n$ points. Note that, in view of Theorem 1.2, $N=N(K)$ is the largest $N$ such that $J(K,N)=\partial K$.

We denote by $|X|$ the $1$-dimensional Hausdorff measure (perimeter) of a set $X\subset \mathbb R ^2$.

Theorem 1.3

Let $\varepsilon >0$, then there is a convex body $K_\varepsilon$ such that

$$\begin{aligned} \frac{|J(K_\varepsilon ,\infty )|}{ |\partial K_\varepsilon |} >1-\varepsilon . \end{aligned}$$

If $K_0$ is a segment or an acute triangle, then we can construct $K_\varepsilon$ as in the previous theorem so that $\lim _{\varepsilon \rightarrow 0}K_\varepsilon =K_0$ in the Hausdorff metric. These examples are also constructed in Sect. 3.

The next theorem is in the Baire category sense (see Sect. 4 and Chap. 20 of [5] for notions and definitions). Let $\mathcal K$ be the set of planar convex bodies together with the Hausdorff metric.

Theorem 1.4

For most convex bodies $K\in \mathcal K$, the set

$$\begin{aligned} \bigcap _{n\in \mathbb N } J(K,n) \end{aligned}$$

contains most points of $\partial K$.

We give the proof of this theorem in Sect. 4.

2 The Finiteness of $N$

First we fix some notation. We write $\mathcal B$ for the closed unit disk, $\mathcal B (Q,r)$ for the closed disk centred at $Q$ with radius $r>0$ and $\mathcal S (Q,r)$ for the circle bounding $B(Q,r)$.

If $K$ is a convex body and $P\in \partial K$, then a line $l$ is a normal of $K$ at $P$ if $P\in l$ and the line orthogonal to $l$ through $P$ supports $K$ at $P$.

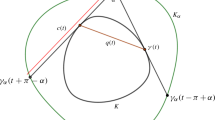
Fix a convex body $K$ and define the set

$$\begin{aligned} \Gamma =\big \{(Q,l):Q\in \partial K,\; l \text{ is } \text{ a } \text{ normal } \text{ of } K \text{ at } Q\big \}. \end{aligned}$$

The set $\Gamma$ is actually a curve, this can be seen by considering the smooth convex body $K^{\prime }=K+\mathcal B$. The set $\Gamma$ is in bijective correspondence with $\partial K^{\prime }$ in the following way: For every point $Q^{\prime }\in \partial K^{\prime }$, let $l$ be the normal line of $K^{\prime }$ at $Q^{\prime }$ and let $Q$ be the point in $l\cap \partial K$ at distance $1$ from $Q^{\prime }$. Then the pair $(Q,l)\in \Gamma$ corresponds to the point $Q^{\prime }\in \partial K^{\prime }$.

The distance between two points $Q_1^{\prime },Q_2^{\prime }\in \partial K^{\prime }$ is the length of the shortest arc of $\partial K^{\prime }$ bounded by these points. We use the above bijection to measure the distance between points in $\Gamma$ and the Euclidean metric to measure distances between points in the plane.

Now we go back to the problem in question. Take $P\in \partial K$ and assume that there are two different points $Q_1,Q_2\in S(P,r)\cap \partial K$. Let $H\subset \partial K$ be the closed arc bounded by $Q_1$ and $Q_2$ that does not contain $P$. Consider the function $g(Q)=\text{ dist }(P,Q)$ for $Q\in H$. Since $g(Q_1)=g(Q_2)$, there exists $Q$ in the relative interior of $H$ such that $g$ attains either its maximum or its minimum on $Q$. For this $Q$ there is a line $l$ so that $(Q,l)\in \Gamma$, and $P\in l$.

Hence, if $P\in \partial K$ is a point such that there are exactly $M$ pairs $(Q,l)\in \Gamma$ with $P\in l$ and $P\ne Q$, then any circle centred at $P$ intersects $\partial K$ in at most $M+1$ points. This implies $N(K)\le M+1$, therefore to prove Theorem 1.2 it is enough to show the following.

Theorem 2.1

Given a convex body $K$, there is a point $P\in \partial K$ such that the number $M$ of pairs $(Q,l)\in \Gamma$ with $P\ne Q$ and $P\in l$ is finite.

It may even be possible that $M$ is bounded by some constant independent of $K$. From the proof it can be seen that $M$ is finite in a positive fraction of the perimeter of $K$.

To prove this theorem we define $\Gamma _0\subset \Gamma$ as the set of pairs $(Q,l)$ for which $l\cap \partial K$ contains exactly one point besides $Q$, let $f(Q,l)$ be this point. We shall study the function $f:\Gamma _0\rightarrow \partial K$.

If $(Q,l)\in \Gamma \setminus \Gamma _0$ then $l\cap \partial K$ contains either one point (namely $Q$) or an infinite number of points (namely an edge of $K$ with $Q$ as an endpoint). In either case, $\partial K$ is not smooth at $Q$ and the internal angle formed at this point is at most $\frac{\pi }{2}$. We call such a point $Q$ a small angle of $K$. Since there are at most 4 small angles on a closed convex curve, $\Gamma \setminus \Gamma _0$ contains at most 8 connected components.

Given $(Q,l)\in \Gamma _0$, define $\alpha (Q,l)$ as the smallest angle between the line $l$ and a supporting line of $K$ at $f(Q,l)$. Note that $\alpha (Q,l)>0$ and that $\alpha :\Gamma _0\rightarrow \mathbb R$ is a lower semi-continuous function and therefore the sets

$$\begin{aligned} \Delta _t=\big \{(Q,l)\in \Gamma _0:\alpha (Q,l)>t\big \} \end{aligned}$$

are open in $\Gamma _0$.

Lemma 2.2

For every $t>0$, the function $f|\Delta _t:\Delta _t\rightarrow \partial K$ is locally Lipschitz. If $D$ is the diameter of $K$, then

$$\begin{aligned} \text{ lip }(f)\le \frac{\max \{1,D\}}{\sin (\frac{t}{2})} \end{aligned}$$

in any small-enough open set of $\Delta _t$.

Proof

Let $(Q,l)\in \Delta _t$ and $P=f(Q,l)$. Since $K$ is convex, there exists $\varepsilon >0$ such that any point $R\in \mathcal B (P,\varepsilon )\cap \partial K$ satisfies $\angle QPR>\frac{t}{2}$ (see Fig. 1a).

It is not difficult to see that there is a $\delta >0$ such that if the pair $(Q^{\prime },l^{\prime })\in \Delta _t$ is at distance less than $\delta$ from $(Q,l)$, then the point $P^{\prime }=f(Q^{\prime },l^{\prime })$ is in $\mathcal B (P,\varepsilon )$.

Since $\text{ dist }(Q,Q^{\prime })\le \text{ dist }((Q,l),(Q^{\prime },l^{\prime }))$ and the angle between $l$ and $l^{\prime }$ is at most $\text{ dist }((Q,l),(Q^{\prime },l^{\prime }))$, the region where $P^{\prime }$ is can be further bounded. If we assume in Fig. 1a that $Q^{\prime }$ is to the left of $Q$, then we have $\angle P^{\prime }QP\le \text{ dist }((Q,l),(Q^{\prime },l^{\prime }))$ if $P^{\prime }$ is right of $P$, and $\text{ dist }(P^{\prime },l)\le \text{ dist }((Q,l),(Q^{\prime },l^{\prime }))$ if $P^{\prime }$ is to the left of $P$. This determines the marked region in Fig. 1b. Thus,

$$\begin{aligned} \text{ dist }(P,P^{\prime })\le \frac{1}{\sin (\frac{t}{2})}\text{ dist }((Q,l),(Q^{\prime },l^{\prime })) \end{aligned}$$

if $P^{\prime }$ is right of $P$, and

$$\begin{aligned} \text{ dist }(P,P^{\prime })\le \frac{\text{ dist }(Q,P^{\prime })}{\sin (\frac{t}{2})}\text{ dist }((Q,l),(Q^{\prime },l^{\prime })) \end{aligned}$$

if $P^{\prime }$ is to the left of $P$. In both cases we have

$$\begin{aligned} \text{ dist }(P,P^{\prime })\le \frac{\max \{1,D\}}{\sin (\frac{t}{2})}\text{ dist }((Q,l),(Q^{\prime },l^{\prime })). \end{aligned}$$

This implies for the Lipschitz constant of $f$ that

$$\begin{aligned} \text{ lip }(f)\le \frac{\max \{1,D\}}{\sin (\frac{t}{2})} \end{aligned}$$

in any small-enough open set of $\Delta _t$. $\square$

Fig. 1

Lemma 2.2

Lemma 2.3

Assume the convex body $K$ is not a polygon with at most $6$ sides. Then there is a set $F\subset \partial K$ with $|F|>0$ and a number $t>0$ such that $f^{-1}(F)\subset \Delta _t$.

Proof

For every small angle $Q\in \partial K$ the set of pairs $(Q,l)\in \Gamma$ is a closed arc, let $(Q,l_+)$ and $(Q,l_-)$ be its boundary points. Define the set $L=\bigcup (l_+\cup l_-)$, where the union is taken over all small angles of $K$.

Since $K$ is not a polygon with at most $6$ sides, then $\partial K\setminus L$ is open relative to $\partial K$ and non-empty. Therefore, there is a closed set $F\subset \partial K\setminus L$ with non-empty interior relative to $\partial K$ (and hence, with positive perimeter).

Suppose that there is a sequence of pairs $\{(Q_i,l_i)\}_{i\in \mathbb N }$ with $f(Q_i,l_i)\in F$ and satisfying $\lim _{i\rightarrow \infty }\alpha (Q_i,l_i)=0$. Let $l_i^{\prime }$ be a supporting line of $K$ at $f(Q_i,l_i)$ that forms an angle of $\alpha (Q_i,l_i)$ with $l_i$. By taking a subsequence if necessary, we may assume that $(Q_i,l_i)$ converges to a pair $(Q,l)$ and that $l_i^{\prime }$ converges to a line $l^{\prime }$. Then $l^{\prime }$ must support $K$ at $(Q,l)$, thus $Q\in L$. This contradicts the definition of $F$, therefore there exists $t>0$ such that $\alpha (Q_i,l_i)>t$ for all $(Q,l)\in F$ and hence $f^{-1}(F)\subset \Delta _t$. $\square$

Proof of Theorem 2.1

If $K$ is a polygon with at most $6$ sides, then for any $P\in \partial K$ the set $f^{-1}(P)$ contains at most $12$ points, so $M\le 12$ there.

Assume now that $K$ is not a polygon with at most $6$ sides and take $F$ as in Lemma 2.3. By Lemma 2.2, $f$ is Lipschitz on $f^{-1}(F)$ and by the coarea formula (see [3]) we obtain

$$\begin{aligned} \int \limits _F \# f^{-1}(P)\text{ d }P =\int \limits _{f^{-1}(F)}\left|\nabla f(Q,l)\right|\,d(Q,l) \le \left|f^{-1}(F)\right|\text{ lip }(f). \end{aligned}$$

Therefore, there is a point $P\in F$ which is taken only finitely many times by $f_{|f^{-1}(F)}$. Since no other pair $(Q,l)\in \Gamma$ with $Q\ne P$ can have $P\in l$, we are done. $\square$

3 Examples

In this section we give examples for Theorems 1.1 and 1.3. First we need a couple of lemmas.

Lemma 3.1

Fix $N\in \mathbb N \cup \{\infty \}$. Let $A,B,C,D$ be points in convex position ordered counter-clockwise such that the angle $\angle ABC\in (0,\frac{\pi }{2})$. For any neighbourhood $V$ of $B$ there is a sequence of points $\{C_i\}_{i=1}^N$ such that:

• (i) The points $D,C,C_1,C_2,\dots B,A$ are all extreme points of their convex hull and are ordered clockwise.

• (ii) For every $P\in [A,B]$ outside of $V$, there is a circle centred at $P$ that intersects the broken line $CC_1C_2\dots BA$ in at least $2N+2$ points.

Proof

Given a point $P$ on the line $AB$, let $\mathcal S _P$ be the circle centred at $P$ that passes through $B$. Let $B^{\prime }\in [A,B]\cap V$ so that $C$ is outside of $\mathcal S _{B^{\prime }}$.

We construct the points $C_i$ inductively starting with $C_0=C$. Once $C_{i-1}$ is constructed, let $C_i$ be a point such that:

• The points $D,C_0,\dots ,C_i,B,A$ are all extreme points of their convex hull and are ordered clockwise,

• $C_i$ is outside of the circle $\mathcal S _{A}$,

• $\angle ABC_i<\frac{\pi }{2}$,

• the segment $(C_{i-1},C_i)$ intersects $\mathcal S _{B^{\prime }}$ twice.

See Fig. 2 for a non-realistic example of this construction. Clearly condition (i) holds.

For a given $P\in [A,B^{\prime }]$ the circle $\mathcal S _P$ is between the circles $\mathcal S _{B^{\prime }}$ and $\mathcal S _A$, therefore $\mathcal S _P$ intersects each of the segments $(C,C_1)$ and $(A,B]$ at least once and each of the segments $(C_i,C_{i+1})$ twice, giving an infinite number of intersections when $N=\infty$. If $N<\infty$, then a circle slightly smaller that $\mathcal S _P$ will, in addition, intersect $(C_N,B)$ twice giving a total of $2N+2$ intersections.

Fig. 2

Lemma 3.1

Lemma 3.2

Let $A_1,B,A_2$ be points in the plane. For $i=1,2$ let $C_i$ be the midpoint of $A_iB$ and $S_i$ be the set of points $P$ such that the orthogonal projection of $P$ on $A_iB$ is contained in the segment $(B,C_i]$. Then for any point $P\in S_1\cap S_2$ there is a circle centred at $P$ that intersects each of the segments $(A_i,B)$ twice.

Proof

Let $P\in S_1\cap S_2$ and assume that $\text{ dist }(P,A_1B)\le \text{ dist }(P,A_2B)$. It is easy to see that there is a real number $r$ larger than $\text{ dist }(P,A_2B)$ and smaller than $\text{ dist }(P,B), \text{ dist }(P,A_1)$ and $\text{ dist }(P,A_2)$. Therefore, the circle centred at $P$ with radius $r$ intersects each of the segments $(A_i,B)$ twice.$\square$

We note that the set of points $P$ that satisfy the conditions in Lemma 3.2 is actually larger. The regions we use are simpler and enough for our purposes.

Now we are ready to construct the examples which prove Theorems 1.1 and 1.3.

Proof of Theorem 1.1

Consider the points

$$\begin{aligned} A_1=(1000,0),\quad A_2=(906,114),\quad A_3=(645,359),\quad A_4=(-498,871). \end{aligned}$$

For $i=1,\dots 4$, let $B_i$ and $C_i$ be the rotation around the origin of $A_i$ by an angle of $2\pi /3$ and $4\pi /3$, respectively. The $12$ points $A_i,B_i,C_i$ are in convex position (see Fig. 3).

Using Lemma 3.2 on the triples $C_1,C_2,C_3$ and $C_2,C_3,C_4$, it can be shown by direct computation that for any point $P$ in some neighbourhood $V$ of the broken line $A_4B_1B_2B_3$ there is a circle centred at $P$ that intersects the broken line $C_1C_2C_3C_4$ in at least $6$ points. This direct computation amounts to checking that the two shaded strips in Fig. 3 together contain the broken line $B_3B_2B_1A_4$ in their interior.

The angle $\angle A_3A_4B_1$ is acute. This is again a simple computation. Lemma 3.1 implies the existence of a point $A_5\in V$ such that for any point $P$ on $[A_3,A_4]\setminus V$ there is a circle centred at $P$ that intersects $A_3A_4A_5B_1$ in at least $4$ points. Define $B_5$ and $C_5$ as above to obtain a 15-gon $K$ having $A_i,B_iC_i$ as its vertices. The radius of the circle $\mathcal S _P$ is close to $|PA_4|$ and therefore intersects $\partial K$ an additional $2$ times, once between $C_3$ and $P$ and once again between $A_5$ and $B_3$.

By the rotational symmetry of the figure, $K$ has the desired property.

It can also be verified that there are points $P\in \partial K$ that are not in $J(K,7)$, for example the midpoint of $[A_3A_4]$. $\square$

Fig. 3

Construction for Theorem 1.1 with the regions from Lemma 3.2

An interactive version of Fig. 3 made with GeoGebra (http://www.geogebra.org) can be found at http://www.geogebratube.org/student/m33469.

Proof of Theorem 1.3

As mentioned before, the convex body $K_{\varepsilon }$ can be constructed so that it is close to any triangle or a straight line segment.

Fix a triangle $A_1A_2A_3$ and let $\varepsilon >0$. Choose points $B_1, B_2$ and $B_3$ so that $A_1B_1A_2B_2A_3B_3$ is a convex 6-gon, each $B_i$ is $\varepsilon$-close to $A_i$ and the angles $\angle A_iB_iA_{i+1}$ are acute. Using Lemma 3.1 with $N=\infty$ on the points $A_iB_iA_{i+1}B_{i+1}$, we obtain three families of points that together with the points $A_i$ and $B_i$ determine the required convex body.

For a straight segment $[A,B]$ a similar thing is done. Choose points $C$ close to $A$ and $D$ close $B$ such that $ACBD$ is a convex $4$-gon and the angles $\angle ACB$ and $\angle ADB$ are acute, then Lemma 3.1 on $BCAD$ and $ADBC$ gives the required convex body. $\square$

4 Generic Behaviour

The set of planar convex bodies $\mathcal K$ with the Hausdorff metric is a complete metric space, thus, it is a Baire space.

The defining property of Baire spaces is that the intersection of countably many dense open sets is also dense. The intersection of countably many open sets is called a $G_\delta$ set. Such sets are considered large. It is said that most points in a Baire space satisfy a property if the set of points satisfying this property contains a dense $G_\delta$ set. These notions can be found in Chap. 20 of [5] and similar techniques are applied in [6].

We prove Theorem 1.4 here, but we need some definitions and lemmas first. Let $K$ be a convex body and assume the circle $\mathcal S$ intersects $\partial K$ at $Q$. If for every $\varepsilon >0$ there are points $Q_1,Q_2\in \mathcal{B }(Q,\varepsilon )\cap \mathcal S$ such that $Q_1\in \text{ int } K$ and $Q_2\not \in K$, then we say that $\mathcal S$ intersects $\partial K$ transversally at $Q$.

To make things simpler, we work with the set $J_0(K,n)\subset J(K,n)$ of points $P\in \partial K$ such that there is a circle centred at $P$ that intersects $\partial K$ transversally in at least $n$ points. If $n<\infty$ then the sets $J_0(K,n)$ are clearly open relative to $\partial K$.

Remark

It can be shown that if $n<\infty$ and $\partial K$ contains no circle-arcs (which is true for most convex bodies) then $J_0(K,n)=J(K,n)$, but we do not need this.

Instead of proving Theorem 1.4 we prove the following stronger statement.

Theorem 4.1

For most convex bodies $K\in \mathcal K$, the set $\bigcap _{n\in \mathbb N } J_0(K,n)$ contains most points of $\partial K$.

Let $\mathcal K _{n,m}$ be the set of convex bodies $K\in \mathcal K$ such that for every point $P\in \partial K$, the set $J_0(K,n)\cap \mathcal B (P,\frac{1}{m})$ is non-empty.

Lemma 4.2

The set $\mathcal K _{n,m}$ is open and dense in $\mathcal K$.

Proof

First we prove that $\mathcal K _{n,m}$ is open. Let $K\in \mathcal K _{n,m}$ and choose a finite family $\{P_i\}$ such that $\{\mathcal{B }(P_i,\frac{1}{2m})\}$ covers $\partial K$. From the definition of $J_0(K,n)$ and the finiteness of $\{P_i\}$, it follows that there exists $\varepsilon >0$ such that whenever $\text{ dist }(K,K^{\prime })<\varepsilon$ the following hold:

• $\{\mathcal{B }(P_i,\frac{1}{2m})\}$ covers $\partial K^{\prime }$,

• if $Q\in J_0(K,n)$ and $Q^{\prime }\in \partial K^{\prime }\cap \mathcal{B }(Q,\varepsilon )$ then $Q^{\prime }\in J_0(K^{\prime },n)$.

This implies that $\mathcal K _{n,m}$ is open.

To show that it is dense, let $K\in \mathcal K$ and $\varepsilon >0$. We construct a convex body $K^{\prime }\in \mathcal K _{n,m}$ such that $\text{ dist }(K,K^{\prime })<\varepsilon$.

Let $K_0$ be a polygon such that $\text{ dist }(K,K_0)< \varepsilon$ and the distance between any two consecutive vertices of $K_0$ is less than $\frac{1}{4m}$. Let $\{P_1,\dots ,P_M\}$ be the set of midpoints of the sides of $K_0$. Given these points we construct new polygons $K_1,\dots ,K_M$ recursively, the following way.

Once $K_{i-1}$ has been constructed, let $Q,R,S$ be consecutive vertices of $K_{i-1}$ such that $R$ is a vertex of $K_{i-1}$ farthest away from $P_i$. Now we remove the vertex $R$ from $K_{i-1}$ and add vertices $R_1,\dots ,R_n$ to form a new polygon $K_i$ with the following properties:

• The points $R_1,\dots ,R_n$ are between $Q$ and $S$,

• the distance between $P_i$ and any $R_j$ is some $r>0$,

• the points $P_1,\dots ,P_M$ belong to $\partial K_i$ and are not vertices of $K_i$,

• $\text{ dist }(K,K_i)<\varepsilon$.

Note that any circle centred at $P_i$ with radius slightly smaller than $r$ will intersect $\partial K_{i-1}$ transversally in at least $n$ points.

It clear that the polygon obtained at the end of this process belongs to $\mathcal K _{n,m}$.$\square$

Proof of Theorem 4.1

By Lemma 4.2 and since $\mathcal K$ is a Baire space, $\bigcap _{n,m\in \mathbb N }\mathcal K _{n,m}$ is a dense $G_\delta$ subset of $\mathcal K$. Let $K\in \bigcap _{n,m\in \mathbb N }\mathcal K _{n,m}$, then each $J_0(K,n)$ is open and dense relative to $\partial K$. Therefore $\bigcap _{n\in \mathbb N } J_0(K,n)$ is a dense $G_\delta$ subset of $\partial K$.$\square$