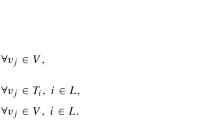Abstract
The Maximum Happy Vertices (MHV) problem and the Maximum Happy Edges (MHE) problem are two fundamental problems arising in the study of the homophyly phenomenon in large scale networks. Both of these two problems are NP-hard. Interestingly, the MHE problem is a natural generalization of Multiway Uncut, the complement of the classic Multiway Cut problem. In this paper, we present new approximation algorithms for MHV and MHE based on randomized LP-rounding technique and non-uniform approach. Specifically, we show that MHV can be approximated within \(\frac{1}{\varDelta +1/g(\varDelta )}\), where \(\varDelta \) is the maximum vertex degree and \(g(\varDelta ) = (\sqrt{\varDelta } + \sqrt{\varDelta +1})^2 \varDelta \), and MHE can be approximated within \(\frac{1}{2} + \frac{\sqrt{2}}{4}f(k) \ge 0.8535\), where \(f(k) \ge 1\) is a function of the color number k. These results improve over the previous approximation ratios for MHV, MHE as well as Multiway Uncut in the literature.



Similar content being viewed by others
References
Anstreicher, K.M.: Linear programming in \(O(\frac{n^3}{\ln n} L)\) operations. SIAM J. Optim. 9(4), 803–812 (1999)
Breiman, L., Friedman, J., Olshen, R., Stone, C.: Classification and Regression Trees. Wadsworth and Brooks, Monterey (1984)
Buchbinder, N., Naor, J., Schwartz, R.: Simplex partitioning via exponential clocks and the multiway cut problem. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) Proceedings of the Annual ACM Symposium on Theory of Computing (STOC), pp. 535–544. Palo Alto, CA, USA (2013)
Calinescu, G., Karloff, H., Rabani, Y.: An improved approximation algorithm for multiway cut. J. Comput. Syst. Sci. 60(3), 564–574 (2000)
Dahlhaus, E., Johnson, D., Papadimitriou, C., Seymour, P., Yannakakis, M.: The complexity of multiterminal cuts. SIAM J. Comput. 23, 864–894 (1994)
Easley, D., Kleinberg, J.: Networks, Crowds, and Markets: Reasoning About a Highly Connected World. Cambridge University Press, Cambridge (2010)
Karger, D., Klein, P., Stein, C., Thorup, M., Young, N.: Rounding algorithms for a geometric embedding of minimum multiway cut. Math. Oper. Res. 29(3), 436–461 (2004)
Kleinberg, J., Tardos, É.: Approximation algorithms for classification problems with pairwise relationships: metric labeling and Markov random fields. J. ACM 49(5), 616–639 (2002)
Langberg, M., Rabani, Y., Swamy, C.: Approximation algorithms for graph homomorphism problems. In: Díaz, J., Jansen, K., Rolim, J.D.P., Zwick, U. (eds.) Proceedings of the 9th International Workshop on Approximation Algorithms for Combinatorial Optimization Problems (APPROX), pp. 176–187. Barcelona, Spain (2006)
Li, A., Li, J., Pan, Y.: Homophyly/kinship hypothesis: natural communities, and predicting in networks. Phys. A 420, 148–163 (2015)
Sharma, A., Vondrák, J.: Multiway cut, pairwise realizable distributions, and descending thresholds. In: Shmoys, D. (ed.) Proceedings of the 46th Annual ACM Symposium on Theory of Computing (STOC), pp. 724–733 (2014)
Vazirani, V.: Approximation Algorithms, 2nd edn. Springer, Berlin (2003)
Williamson, D.P., Shmoys, D.B.: The Design of Approximation Algorithms. Cambridge University Press, Cambridge (2011)
Zhang, P., Jiang, T., Li, A.: Improved approximation algorithms for the maximum happy vertices and edges problems. In: Xu, D., Du, D., Du, D.-Z. (eds.) Proceedings of the 21th International Computing and Combinatorics Conference (COCOON), Volume 9198 of LNCS, pp. 159–170 (2015)
Zhang, P., Li, A.: Algorithmic aspects of homophyly of networks. Theor. Comput. Sci. 593, 117–131 (2015)
Acknowledgements
We thank the anonymous reviewers for their suggestions which help to improve the presentation of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Peng Zhang is supported by the State Scholarship Fund of China, NSFC 61672323, NSF of Shandong Province (ZR2015FM008, ZR2016AM28), and the Fundamental Research Funds of Shandong University (2015JC006). Most of his work was done when the author was visiting University of California at Riverside, USA. Angsheng Li is supported by the hundred talent program of the Chinese Academy of Sciences, and the National Basic Research Program (973) of China (2014CB340302). Guohui Lin is partially supported by the NSERC and his work was mostly done during his sabbatical leave at the Kyushu Institute of Technology, Iizuka Campus. Eiji Miyano is partially supported by the Grants-in-Aid for Scientific Research of Japan (KAKENHI) under Grant No. 26330017.
Appendix: An Example of MHV
Appendix: An Example of MHV
In the MHV instance in Fig. 3, there are k vertices \(s_1\), \(s_2\), \(\ldots \), \(s_k\) with the pre-specified colors \(1, 2, \ldots , k\), respectively. The remaining vertices \(t_1\), \(t_2\), \(\ldots \), \(t_k\), and u are uncolored. Every vertex has unit weight. Since each \(t_i\) (\(1\le i \le k\)) is adjacent to \(s_1\), \(s_2\), \(\ldots \), \(s_k\), an optimal solution is to color \(t_1\), \(t_2\), \(\ldots \), \(t_k\), and u in color 1 and the optimum is 2.
Then consider the fractional optimal value \(\text{ OPT }_f = \sum _v\sum _{i=1}^k x_v^i\) of linear program (LP-V) on the instance in Fig. 3. For a vertex v, define \(x_v = \sum _{i=1}^k x_v^i\); this is the fraction to which vertex v is happy in a fractional solution. Denote by \((y_v^1, y_v^2, \ldots , y_v^k)\) the color vector assigned to vertex v. Then the color vectors of \(s_1\), \(s_2\), \(\ldots \), \(s_k\) are \((1, 0, \ldots , 0)\), \((0, 1, \ldots , 0)\), and \((0, \ldots , 0, 1)\), respectively. Since each \(t_i\) (\(1\le i \le k\)) is adjacent to \(s_1\), \(s_2\), \(\ldots \), \(s_k\), no matter what color vector is assigned to \(t_i\), \(t_i\) cannot be happy to any fraction (that is, \(x_{t_i} = 0\)).
For each \(s_i\) (\(1 \le i \le k\)), and for all colors \(j \ne i\), \(x_{s_i}^j\) is always zero; only \(x_{s_i}^i\) can be greater than zero. Since each \(s_i\) is adjacent to \(t_1\), \(t_2\), \(\ldots \), \(t_k\), and since \(x_{s_i}^i = \min _{u\in B(s_i)} \{y_u^i\}\), this means the minimum of \(y_{t_1}^i\), \(y_{t_2}^i\), and \(y_{t_k}^i\) is greater than zero. Since the optimal solution would make \(x_{s_i}^i\) as large as possible, and since the structures of all \(s_i\)’s in the instance are symmetric, the optimal solution must assign color vector \((\frac{1}{k}, \frac{1}{k}, \ldots , \frac{1}{k})\) to each \(t_i\). As a result, the same color vector will be assigned to vertex u.
In this optimal solution, \(x_{s_i} = \frac{1}{k}\) for \(1\le i \le k\), \(x_u = \sum _i x_u^i = \sum _i \frac{1}{k} = 1\). Therefore, the fractional optimum \(\text{ OPT }_f = 2\).
Since \(\sum _{i=1}^k y_v^i = 1\), it is natural to color vertex v in color i using \(\{y_v^i\}\) as a distribution. However, this randomized coloring scheme only gives poor expected approximation ratio on the instance in Fig. 3. The analysis is given below.
For each \(1 \le i \le k\),
So,
For each \(1 \le i \le k\),
Therefore, the expected solution value is \(\left( \frac{1}{k}\right) ^k + k \cdot \left( \frac{1}{k}\right) ^k = \left( 1+\frac{1}{k}\right) \frac{1}{k^{k-1}}\). Consequently, the expected approximation ratio (using \(\text{ OPT }_f\) as an upper bound of \(\text{ OPT }\)) is \(\varOmega \left( \frac{1}{k^{k-1}}\right) \), which is \(\varOmega \left( \frac{1}{(\varDelta -1)^{\varDelta -2}}\right) \), as the maximum degree is \(k+1\) in the instance.
Rights and permissions
About this article
Cite this article
Zhang, P., Xu, Y., Jiang, T. et al. Improved Approximation Algorithms for the Maximum Happy Vertices and Edges Problems. Algorithmica 80, 1412–1438 (2018). https://doi.org/10.1007/s00453-017-0302-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00453-017-0302-8
Keywords
- Maximum Happy Vertices
- Maximum Happy Edges
- Approximation algorithm
- Randomized rounding
- Network homophyly