Sparsification Upper and Lower Bounds for Graph Problems and Not-All-Equal SAT

Abstract

We present several sparsification lower and upper bounds for classic problems in graph theory and logic. For the problems 4-Coloring, (Directed) Hamiltonian Cycle, and (Connected) Dominating Set, we prove that there is no polynomial-time algorithm that reduces any n-vertex input to an equivalent instance, of an arbitrary problem, with bitsize $O(n^{2-\varepsilon })$ for $\varepsilon > 0$, unless $\mathsf {NP \subseteq coNP/poly}$ and the polynomial-time hierarchy collapses. These results imply that existing linear-vertex kernels for k-Nonblocker and k-Max Leaf Spanning Tree (the parametric duals of (Connected) Dominating Set) cannot be improved to have $O(k^{2-\varepsilon })$ edges, unless $\mathsf {NP \subseteq coNP/poly}$. We also present a positive result and exhibit a non-trivial sparsification algorithm for d-Not-All-Equal-SAT. We give an algorithm that reduces an n-variable input with clauses of size at most d to an equivalent input with $O(n^{d-1})$ clauses, for any fixed d. Our algorithm is based on a linear-algebraic proof of Lovász that bounds the number of hyperedges in critically 3-chromatic d-uniform n-vertex hypergraphs by $\left( {\begin{array}{c}n\\ d-1\end{array}}\right)$. We show that our kernel is tight under the assumption that $\mathsf {NP} \nsubseteq \mathsf {coNP}/\mathsf {poly}$.

1 Introduction

1.1 Background

Sparsification refers to the method of reducing an object such as a graph or CNF-formula to an equivalent object that is less dense, that is, an object in which the ratio of edges to vertices (or clauses to variables) is smaller. The notion is fruitful in theoretical [16] and practical (cf. [10]) settings when working with (hyper)graphs and formulas. The theory of kernelization, originating from the field of parameterized complexity theory, can be used to analyze the limits of polynomial-time sparsification. Using tools developed in the last five years, it has become possible to address questions such as: “Is there a polynomial-time algorithm that reduces an n-vertex instance of my favorite graph problem to an equivalent instance with a subquadratic number of edges?”

The impetus for this line of analysis was given by an influential paper by Dell and van Melkebeek [8] (conference version in 2010). One of their main results states that if there is an $\varepsilon > 0$ and a polynomial-time algorithm that reduces any n-vertex instance of Vertex Cover to an equivalent instance, of an arbitrary problem, that can be encoded in $O(n^{2-\varepsilon })$ bits, then $\mathsf {NP \subseteq coNP/poly}$ and the polynomial-time hierarchy collapses. Since any nontrivial input (G, k) of Vertex Cover has $k \le n = |V(G)|$, their result implies that the number of edges in the 2k-vertex kernel for k-Vertex Cover [22] cannot be improved to $O(k^{2-\varepsilon })$ unless $\mathsf {NP \subseteq coNP/poly}$.

Using related techniques, Dell and van Melkebeek also proved important lower bounds for d-cnf-sat problems: testing the satisfiability of a propositional formula in conjunctive normal form (CNF), where each clause has at most d literals. They proved that for every fixed integer $d \ge 3$, the existence of a polynomial-time algorithm that reduces any n-variable instance of d-cnf-sat to an equivalent instance, of an arbitrary problem, with $O(n^{d-\varepsilon })$ bits for some $\varepsilon > 0$, implies $\mathsf {NP \subseteq coNP/poly}$. Their lower bound is tight: there are $O(n^d)$ possible clauses of size d over n variables, allowing an instance to be represented by a vector of $O(n^d)$ bits that specifies for each clause whether or not it is present.

1.2 Our Results

We continue this line of investigation and analyze sparsification for several classic problems in graph theory and logic. We obtain several sparsification lower bounds that imply that the quadratic number of edges in existing linear-vertex kernels is likely to be unavoidable. When it comes to problems from logic, we give the—to the best of our knowledge—first example of a problem that does admit nontrivial sparsification: d-Not-All-Equal-SAT. We also provide a matching lower bound.

The first problem we consider is 4-Coloring, which asks whether the input graph has a proper vertex coloring with four colors. Using several new gadgets, we give a cross-composition [3] to show that the problem has no compression of size $O(n^{2-\varepsilon })$ unless $\mathsf {NP \subseteq coNP/poly}$. To obtain the lower bound, we give a polynomial-time construction that embeds the logical or of a series of t size-n inputs of an NP-hard problem into a graph $G'$ with $O(\sqrt{t} \cdot n^{O(1)})$ vertices, such that $G'$ has a proper 4-coloring if and only if there is a yes-instance among the inputs. The main structure of the reduction follows the approach of Dell and Marx [7]: we create a table with two rows and $O(\sqrt{t})$ columns and $O(n^{O(1)})$ vertices in each cell. For each way of picking one cell from each row, we aim to embed one instance into the edge set between the corresponding groups of vertices. When the NP-hard starting problem is chosen such that the t inputs each decompose into two induced subgraphs with a simple structure, one can create the vertex groups and their connections such that for each pair of cells (i, j), the subgraph they induce represents the $i \cdot \sqrt{t} + j$-th input. If there is a yes-instance among the inputs, this leads to a pair of cells that can be properly colored in a structured way. The challenging part of the reduction is to ensure that the edges in the graph corresponding to no-inputs do not give conflicts when extending this partial coloring to the entire graph.

It is easy to see that the lower bound for 4-Coloring implies that d-Coloring with $d \ge 4$ has no compression of size $O(n^{2-\varepsilon })$ unless $\mathsf {NP \subseteq coNP/poly}$, since any instance of 4-Coloring can be transformed into an instance of d-Coloring by adding $d-4$ new universal vertices. The existence of a non-trivial sparsification for 3-Coloring remains unknown (see Sect. 7).

The next problem we attack is Hamiltonian Cycle. We rule out compressions of size $O(n^{2-\varepsilon })$ for the directed and undirected variant of the problem, assuming $\mathsf {NP} \nsubseteq \mathsf {coNP}/\mathsf {poly}$. The construction is inspired by kernelization lower bounds for Directed Hamiltonian Cycle parameterized by the vertex-deletion distance to a directed graph whose underlying undirected graph is a path [2].

By combining gadgets from kernelization lower bounds for two different parameterizations of Red Blue Dominating Set, we prove that there is no compression of size $O(n^{2-\varepsilon })$ for Dominating Set unless $\mathsf {NP \subseteq coNP/poly}$. The same construction rules out subquadratic compressions for Connected Dominating Set. These lower bounds have implications for the kernelization complexity of the parametric duals Nonblocker and Max Leaf Spanning Tree of (Connected) Dominating Set. For both Nonblocker and Max Leaf there are kernels with $O(k)$ vertices [6, 11] that have ${\varTheta }(k^2)$ edges. Our lower bounds imply that the number of edges in these kernels cannot be improved to $O(k^{2-\varepsilon })$, unless $\mathsf {NP \subseteq coNP/poly}$.

The final family of problems we consider is d-Not-All-Equal-SAT for $d~\ge ~4$ fixed. The input consists of a CNF-formula with at most d literals per clause. The question is whether there is an assignment to the variables such that each clause contains both a literal that evaluates to true and one that evaluates to false. There is a simple linear-parameter transformation from d-cnf-sat to $(d+1)$-nae-sat that consists of adding one variable that occurs as a positive literal in all clauses. By the results of Dell and van Melkebeek discussed above, this implies that d-nae-sat does not admit compressions of size $O(n^{d-1-\varepsilon })$ unless $\mathsf {NP \subseteq coNP/poly}$. We prove the surprising result that this lower bound is tight! A linear-algebraic result due to Lovász [21], concerning the size of critically 3-chromatic d-uniform hypergraphs, can be used to give a kernel for d-nae-sat with $O(n^{d-1})$ clauses for every fixed d. The kernel is obtained by computing the basis of an associated matrix and removing the clauses that can be expressed as a linear combination of the basis clauses¹.

1.3 Related Work

Dell and Marx introduced the table structure for compression lower bounds [7] in their study of compression for packing problems. Hermelin and Wu [15] analyzed similar problems. Other papers about polynomial kernelization and sparsification lower bounds include [5, 18].

2 Preliminaries

A parameterized problem $Q$ is a subset of ${\varSigma }^* \times \mathbb {N}$, where ${\varSigma }$ is a finite alphabet. Let $Q,Q '\subseteq {\varSigma }^*\times \mathbb {N}$ be parameterized problems and let $h:\mathbb {N} \rightarrow \mathbb {N}$ be a computable function. A generalized kernel for $Q$ into $Q '$ of size h(k) is an algorithm that, on input $(x, k)\in {\varSigma }^*\times \mathbb {N}$, takes time polynomial in $|x| + k$ and outputs an instance $(x', k')$ such that:

• 1. $|x'|$ and $k'$ are bounded by h(k), and

• 2. $(x', k') \in Q '$ if and only if $(x, k) \in Q$.

The algorithm is a kernel for $Q$ if $Q '=Q$. It is a polynomial (generalized) kernel if h(k) is a polynomial.

Since a polynomial-time reduction to an equivalent sparse instance yields a generalized kernel, we will use the concept of generalized kernels in the remainder of this paper to prove the non-existence of such sparsification algorithms. We employ the cross-composition framework by Bodlaender et al. [3], which builds on earlier work by several authors [1, 8, 13].

Definition 1

(Polynomial equivalence relation) An equivalence relation $\mathscr {R}$ on ${\varSigma }^*$ is called a polynomial equivalence relation if the following conditions hold.

• 1. There is an algorithm that, given two strings $x, y \in {\varSigma }^*$, decides whether x and y belong to the same equivalence class in time polynomial in $|x| + |y|$.

• 2. For any finite set $S \subseteq {\varSigma }^*$ the equivalence relation $\mathscr {R}$ partitions the elements of S into a number of classes that is polynomially bounded in the size of the largest element of S.

Definition 2

(Cross-composition) Let $L\subseteq {\varSigma }^*$ be a language, let $\mathscr {R}$ be a polynomial equivalence relation on ${\varSigma }^*$, let $Q \subseteq {\varSigma }^*\times \mathbb {N}$ be a parameterized problem, and let $f :\mathbb {N} \rightarrow \mathbb {N}$ be a function. An $\textsc {or}$ -cross-composition of L into $Q$ (with respect to $\mathscr {R}$) of cost f(t) is an algorithm that, given t instances $x_1, x_2, \ldots , x_t \in {\varSigma }^*$ of L belonging to the same equivalence class of $\mathscr {R}$, takes time polynomial in $\sum _{i=1}^t |x_i|$ and outputs an instance $(y, k) \in {\varSigma }^* \times \mathbb {N}$ such that:

• 1. the parameter k is bounded by $O(f(t)\cdot (\max _i|x_i|)^c)$, where c is some constant independent of t, and

• 2. $(y, k) \in Q$ if and only if there is an $i \in [t]$ such that $x_i \in L$.

Theorem 1

([3]) Let $L\subseteq {\varSigma }^*$ be a language, let $Q \subseteq {\varSigma }^*\times \mathbb {N}$ be a parameterized problem, and let $d, \varepsilon$ be positive reals. If L is NP-hard under Karp reductions, has an $\textsc {or}$-cross-composition into $Q$ with cost $f(t)=t^{1/d+o(1)}$, where t denotes the number of instances, and $Q$ has a polynomial (generalized) kernelization with size bound $O(k^{d-\varepsilon })$, then $\mathsf {NP \subseteq coNP/poly}$.

For $r \in \mathbb {N}$ we will refer to an $\textsc {or}$-cross-composition of cost $f(t) = t^{1/r} \log (t)$ as a degree-r cross-composition. By Theorem 1, a degree-r cross-composition can be used to rule out generalized kernels of size $O(k^{r - \varepsilon })$. We frequently use the fact that a polynomial-time linear-parameter transformation from problem $Q$ to $Q '$ implies that any generalized kernelization lower bound for $Q$, also holds for $Q '$ (cf. [3, 4]). Let [r] be defined as $[r]~:=~\{x~\in ~\mathbb {N}~\mid ~1~\le ~x~\le ~r\}$.

Fig. 1

Treegadgets of height two with example colorings. The solid shading is referred to as red. Treegadget with no red leaf (a) and where one of the leaves is red (b) (Color figure online)

3 Graph Coloring

In this section we analyze the 4-Coloring problem, which asks whether it is possible to assign each vertex of the input graph one out of 4 possible colors, such that there is no edge whose endpoints share the same color. We show that 4-Coloring does not have a generalized kernel of size $O(n^{2-\varepsilon })$, by giving a degree-2 cross-composition from a tailor-made problem that will be introduced below. Before giving the construction, we first present and analyze some of the gadgets that will be needed.

Definition 3

A treegadget is the graph obtained from a complete binary tree by replacing each vertex v by a triangle on vertices $r_v$, $x_v$ and $y_v$. Let $r_v$ be connected to the parent of v and let $x_v$ and $y_v$ be connected to the left and right subtree of v. An example of a treegadget with eight leaves is shown in Fig. 1 . If vertex v is the root of the tree, then $r_v$ is called the root of the treegadget. If v is a leaf of the complete binary tree, we call the corresponding vertices $x_v$ and $y_v$ leaves of the treegadget. Let the height of a treegadget be equal to the height of its corresponding binary tree.

It is easy to see that a treegadget is 3-colorable. The important property of this gadget is that if there is a color that does not appear on any leaf in a proper 3-coloring, then this must be the color of the root. See Fig. 1a for an illustration.

Lemma 1

Let T be a treegadget with root r and let $c :V(T) \rightarrow \{1, 2, 3\}$ be a proper 3-coloring of T. If $k \in \{1, 2, 3\}$ such that $c(v) \ne k$ for every leaf v of T, then $c(r) = k$.

Proof

This will be proven using induction on the structure of a treegadget. For a single triangle, the result is obvious. Suppose we are given a treegadget of height h and that the statement holds for all treegadgets of smaller height. Consider the top triangle r, x, y where r is the root. Then, by the induction hypothesis, the roots of the left and right subtree are colored using k. Hence x and y do not use color k. Since x, y, r is a triangle, r has color k in the 3-coloring. $\square$

The following lemma will be used in the correctness proof of the cross-composition to argue that the existence of a single yes-input is sufficient for 4-colorability of the entire graph.

Lemma 2

Let T be a treegadget with leaves $L\subseteq V(T)$ and root r. Any 3-coloring $c' :L \rightarrow \{1, 2, 3\}$ that is proper on T[L] can be extended to a proper 3-coloring of T. If there is a leaf $v\in L$ such that $c'(v)=i$, then such an extension exists with $c(r) \ne i$.

Proof

We will prove this by induction on the height of the treegadget. For a single triangle, the result is obvious. Suppose the lemma is true for all treegadgets up to height $h-1$ and we are given a treegadget of height h with root triangle r, x, y and with coloring of the leaves $c'$. Let one of the leaves be colored using i. Without loss of generality assume this leaf is in the left subtree, whose root $r_1$ is connected to x. By the induction hypothesis, we can extend the coloring restricted to the leaves of the left subtree to a proper 3-coloring of the left subtree such that $c(r_1) \ne i$. We assign color i to x. Since $c'$ restricted to the leaves in the right subtree is a proper 3-coloring of the leaves in the right subtree, by induction we can extend that coloring to a proper 3-coloring of the right subtree. Suppose the root of this subtree gets color $j \in \{1, 2, 3\}$. We now color y with a color $k \in \{1, 2, 3\}\setminus \{i, j\}$, which must exist. Finally, choose $c(r) \in \{1, 2, 3\} \setminus \{i, k\}$. By definition, the vertices r, y, and x are now assigned a different color. Both x and y have a different color than the root of their corresponding subtree, thereby c is a proper coloring. We obtain that the defined coloring c is a proper coloring extending $c'$ with $c(r)\ne i$. $\square$

Fig. 2

Triangular gadget with proper 3-coloring

Definition 4

A triangular gadget is a graph on 12 vertices depicted in Fig. 2. Vertices u, v, and w are the corners of the gadget, all other vertices are referred to as inner vertices.

It is easy to see that a triangular gadget is always 3-colorable in such a way that every corner gets a different color. Furthermore, unlike a triangle, a triangular gadget can be 4-colored such that all corners receive the same color. Moreover, we make the following observation.

Observation 1

Let G be a triangular gadget with corners u, v, and w, and let $c~:~V(G)~\rightarrow ~\{1, 2, 3\}$ be a proper 3-coloring of G. Then $c(v) \ne c(u) \ne c(w) \ne c(v)$. Furthermore, every partial coloring that assigns distinct colors to the three corners of a triangular gadget can be extended to a proper 3-coloring of the entire gadget.

Having presented all the gadgets we use in our construction, we now define the source problem for the cross-composition. It is a variant of the problem that was used to prove kernel lower bounds for Chromatic Number parameterized by vertex cover [3].

Lemma 3

The 2-3-Coloring with Triangle Split Decomposition problem is NP-complete.

Proof

It is easy to verify the problem is in NP. We will show that it is NP-hard by giving a reduction from 3-nae-sat, which is known to be NP-complete [14]. Suppose we are given formula $F = C_1 \wedge C_2 \wedge \ldots \wedge C_m$ over the set of variables U. Construct graph G in the following way. For every variable $x \in U$, construct a gadget as depicted in Fig. 3a containing vertices x and $\lnot x$. For every clause $C_i$, construct a triangle on vertices $v_1^i, v_2^i$ and $v_3^i$ as depicted in Fig. 3b. For each clause $C_i = (\ell _1 \vee \ell _2 \vee \ell _3)$ for $i \in [m]$, connect the vertex representing literal $\ell _j$ for $j \in \{1, 2, 3\}$ to vertex $v_j^i$ in G.

It is easy to verify that G has a triangle split decomposition with X consisting of the vertices representing literals and Y consisting of the remaining vertices. In Fig. 3, triangles are shown with white vertices and the independent set is shown in black.

Suppose G is 2-3-colorable with color function $c :V(G) \rightarrow \{1, 2, 3\}$ such that $c(v)~\in ~\{1, 2\}$ for all v in the independent set X. To satisfy F, let variable x be true if and only if $c(x) = 2$, i.e., if the vertex representing the positive literal x is colored 2. To show that this results in a satisfying assignment, consider any clause $C_i$ for $i \in [m]$. Note that $c(x) = 2 \Leftrightarrow c(\lnot x) = 1$, as the gadget prevents x and $\lnot x$ from having the same color and they are both colored with 1 or 2. The triangle $\{v_1^i, v_2^i, v_3^i\}$ for clause $C_i$ contains a vertex $v^i_j$ such that $c(v_j^i) = 1$ and a vertex $v_k^i$ such that $c(v_k^i) = 2$ for $j, k \in [3]$, otherwise it is not properly colored. Since vertex $\ell _j$ is connected to $v^i_j$, it follows that $c(\ell _j) \ne 1$, implying $c(\ell _j) = 2$. If $\ell _j$ is a positive literal this immediately implies $\ell _j$ evaluates to true in our chosen assignment. If $\ell _j$ is a negative literal the same conclusion follows from the fact that it is colored 2 if and only if the corresponding positive literal is colored 1. Similarly, $c(\ell _k) \ne 2$ implies that $c(\ell _k) = 1$ and literal $\ell _k$ evaluates to false. Therefore any clause $C_i$ is NAE-satisfied by this assignment.

Suppose F is a yes-instance, with satisfying truth assignment S. Define color function $c:V(G)\rightarrow \{1, 2, 3\}$ as $c(x) := 1$ and $c(\lnot x) := 2$ if x is set to false in S, define $c(x) := 2$ and $c(\lnot x) := 1$ otherwise. Color the remainder of the variable gadgets consistently. We now need to show how to color the clause gadgets. Consider any clause $C_i = (\ell _1\vee \ell _2\vee \ell _3)$. At least one of the literals evaluates to true and one to false. By symmetry we assume $\ell _1$ is true and $\ell _2$ is false. We then set $c(v_1^i) := 1$, $c(v_2^i):= 2$, and $c(v_3^i) := 3$ in the clause gadget of $C_i$. It is easy to check that c is a proper 2-3-coloring of G. $\square$

Theorem 2

4-Coloring parameterized by the number of vertices n does not have a generalized kernel of size $O(n^{2-\varepsilon })$ for any $\varepsilon > 0$, unless $\mathsf {NP \subseteq coNP/poly}$.

Proof

By Theorem 1 and Lemma 3 it suffices to give a degree-2 cross-composition from the 2-3-coloring problem defined above into 4-Coloring parameterized by the number of vertices. For ease of presentation, we will actually give a cross-composition into the 4-List Coloring problem, whose input consists of a graph G and a list function that assigns every vertex $v \in V(G)$ a list $L(v) \subseteq [4]$ of allowed colors. The question is whether there is a proper coloring of the graph in which every vertex is assigned a color from its list. The 4-List Coloring problem reduces to the ordinary 4-Coloring by a simple transformation that adds a 4-clique to enforce the color lists, which will prove the theorem. For now, we focus on giving a cross-composition into 4-List Coloring. $\square$

Fig. 3

The gadgets constructed for the variables (a) and the clauses (b) of formula F

Fig. 4

The graph $G'$ for $t'= 4$, $m = 3$, and $n=2$. Edges between vertices in S and T are left out for simplicity

We start by defining a polynomial equivalence relation on inputs of 2-3-Coloring with Triangle Split Decomposition. Let two instances be equivalent under equivalence relation $\mathscr {R}$ when set Y induces the same number of triangles and the independent sets X have the same size. It is easy to see that $\mathscr {R}$ is a polynomial equivalence relation. By duplicating one of the inputs, we can ensure that the number of inputs to the cross-composition is an even power of two; this does not change the value of or, and increases the total input size by at most a factor four. We will therefore assume that the input consists of t instances of 2-3-Coloring with Triangle Split Decomposition such that $t = 2^{2i}$ for some integer i, implying that $\sqrt{t}$ and $\log \sqrt{t}$ are integers. Let $t':= \sqrt{t}$. Enumerate the instances as $X_{i, j}$ for $1\le i, j \le t'$. Each input $X_{i, j}$ consists of a graph $G_{i, j}$ and a partition of its vertex set into sets U and V, such that U is an independent set of size m and $G_{i, j}[V]$ consists of n vertex-disjoint triangles. Enumerate the vertices in U and V as $u_1,\ldots , u_m$ and $v_1, \ldots , v_{3n}$, such that vertices $v_{3\ell -2}, v_{3\ell -1}$ and $v_{3\ell }$ form a triangle, for $\ell \in [n]$. We will create an instance $G'$ of the 4-List Coloring problem, which consists of a graph $G'$ and a list function L that assigns each vertex a subset of the color palette $\{x, y, z, a\}$. Refer to Fig. 4 for a sketch of $G'$.

• 1. Initialize $G'$ as the graph containing $t'$ sets of m vertices each, called $S_i$ for $i~\in ~[t']$. Label the vertices in each of these sets as $s^i_\ell$ for $i \in [t']$, $\ell \in [m]$ and let $L(s^i_\ell )~:=~\{x, y, a\}$.

• 2. Add $t'$ sets of n triangular gadgets each, labeled $T_j$ for $j \in [t']$. Label the corner vertices in $T_j$ as $t_\ell ^j$ for $\ell \in [3n]$, such that vertices $t_{3\ell -2}^j, t_{3\ell -1}^j$ and $t_{3\ell }^j$ are the corner vertices of one of the gadgets for $\ell \in [n]$. Let $L(t_\ell ^j) := \{x, y, z\}$ and for any inner vertex v of a triangular gadget, let $L(v) := \{x, y, z, a\}$.

• 3. Connect vertex $s^i_k$ to vertex $t^j_\ell$ if in graph $G_{i, j}$ vertex $u_k$ is connected to $v_\ell$, for $k \in [m]$ and $\ell \in [3n]$. By this construction, the subgraph of $G'$ induced by $S_i \cup T_j$ is isomorphic to the graph obtained from $G_{i, j}$ by replacing each triangle with a triangular gadget.

• 4. Add a treegadget $G_S$ with $t'$ leaves to $G'$ and enumerate these leaves as $1,\ldots , t'$; recall that $t'$ is a power of two. Connect the i’th leaf of $G_S$ to every vertex in $S_i$. Let the root of $G_S$ be $r_S$ and define $L(r_S) := \{x, y\}$. For every other vertex v in $G_S$ let $L(v) := \{x, y, a\}$.

• 5. Add a treegadget $G_T$ with $2t'$ leaves to $G'$ and enumerate these leaves as $1, \ldots , 2t'$. For $j \in [t']$, connect every inner vertex of a triangular gadget in group $T_j$ to leaf number $2j-1$ of $G_T$. For every leaf v with an even index let $L(v) := \{y, z\}$ and let the root $r_T$ have list $L(r_T) := \{y, z\}$. For every other vertex v of gadget $G_T$ let $L(v) := \{y, z, a\}$.

Claim

The graph $G'$ is 4-list-colorable $\Leftrightarrow$ some input instance $X_{i^*j^*}$ is 2-3-colorable.

Proof

$(\Rightarrow )$ Suppose we are given a 4-list coloring c for $G'$. By definition, $c(r_S) \ne a$. From Lemma 1 it follows that there is a leaf v of $G_S$ such that $c(v) = a$. This leaf is connected to all vertices in some $S_{i^*}$, which implies that none of the vertices in $S_{i^*}$ are colored using a. Therefore all vertices in $S_{i^*}$ are colored using x and y. Similarly the gadget $G_T$ has at least one leaf v such that $c(v) = a$, note that this must be a leaf with an odd index. Therefore there exists $T_{j^*}$ where all vertices are colored using x, y or z. Thereby in $S_{i^*} \cup T_{j^*}$ only three colors are used, such that $S_{i^*}$ is colored using only two colors. Using Observation 1 and the fact that $G'[S_{i^*} \cup T_{j^*}]$ is isomorphic to the graph obtained from $G_{i^*, j^*}$ by replacing triangles by triangular gadgets, we conclude that $X_{i^*j^*}$ has a proper 2-3-coloring.

$(\Leftarrow )$ Suppose $c :V(G_{i^*, j^*}) \rightarrow \{x, y, z\}$ is a proper 2-3-coloring for $X_{i^*, j^*}$, such that the U-partite set of $G_{i^*, j^*}$ is colored using only x and y. We will construct a 4-list coloring $c' :V(G') \rightarrow \{x, y, z, a\}$ for $G'$. For $u_k$, $k\in [m]$ in instance $X_{i^*, j^*}$ let $c'(s^{i^*}_k) := c(u_k)$ and for $v_\ell$ for $\ell \in [3n]$ let $c'(t^{j^*}_\ell ) := c(v_\ell )$. Let $c'(s^i_\ell ) := a$ for $i \ne i^*$ and $\ell \in [n]$, furthermore let $c'(t^j_\ell ) := z$ for $j \ne j^*$ and $\ell \in [3m]$. For triangular gadgets in $T_{j^*}$ the coloring $c'$ defines all corners to have distinct colors; by Observation 1 we can color the inner vertices consistently using $\{x, y, z\}$. For $T_j$ with $j\in [t']$ and $j \ne j^*$, the corners of triangular gadgets have color z and we can now consistently color the inner vertices using $\{x, y, a\}$.

The leaf of gadget $G_S$ that is connected to $S_{i^*}$ can be colored using a. Every other leaf can use both x and y, so we can properly 3-color the leaves such that one leaf has color a. From Lemma 2 it follows that we can consistently 3-color $G_S$ such that the root $r_S$ does not receive color a, as required by $L(r_S)$. Similarly, in triangular gadgets in $T_{j^*}$ the inner vertices do not have color a. As such, leaf $2j^*-1$ of $G_T$ can be colored using a and we color leaf $2j^*$ with y. For $j \in [t']$ with $j \ne j^*$ color leaf $2j - 1$ with z and leaf 2j using y. Now the leaves of $G_T$ are properly 3-colored and one is colored a. It follows from Observation 1 that we can color $G_T$ such that the root is not colored a. This completes the 4-list coloring of $G'$. $\square$

The claim shows that the construction serves as a cross-composition into 4-List Coloring. To prove the theorem, we add four new vertices to simulate the list function. Add a clique on four vertices $\{x, y, z, a\}$. If for any vertex v in $G'$, some color is not contained in L(v), connect v to the vertex corresponding to this color. As proper colorings of the resulting graph correspond to proper list colorings of $G'$, the resulting graph is 4-colorable if and only if there is a yes-instance among the inputs. It remains to bound the parameter of the problem, i.e., the number of vertices. Observe that a treegadget has at least as many leaves as its corresponding binary tree, therefore the graph $G'$ has at most $12mt'+nt'+ 6t'+ 12t'+ 4 = O(t'\cdot (m+n)) = O(\sqrt{t}\max |X_{i, j}|)$ vertices. Theorem 2 now follows from Theorem 1 and Lemma 3.$\square$

Fig. 5

Path gadget for Theorem 3

4 Hamiltonian Cycle

In this section we prove a sparsification lower bound for Hamiltonian Cycle and its directed variant by giving a degree-2 cross-composition. The starting problem is Hamiltonian $s-t$ path on bipartite graphs.

It is known that Hamiltonian path is NP-complete on bipartite graphs [14] and it is easy to see that is remains NP-complete when fixing a degree 1 start and endpoint.

Theorem 3

(Directed) Hamiltonian Cycle parameterized by the number of vertices n does not have a generalized kernel of size $O(n^{2 - \varepsilon })$ for any $\varepsilon > 0$, unless $\mathsf {NP \subseteq coNP/poly}$.

Proof

By a suitable choice of polynomial equivalence relation, and by padding the number of inputs, it suffices to give a cross-composition from the $s-t$ problem on bipartite graphs when the input consists of t instances $X_{i, j}$ for $i, j \in [\sqrt{t}]$ (i.e., $\sqrt{t}$ is an integer), such that each instance $X_{i, j}$ encodes a bipartite graph $G_{i, j}$ with partite sets $A^*_{i, j}$ and $B^*_{i, j}$ with $|A^*_{i, j}| = m$ and $|B^*_{i, j}| = n = m+1$, for some $m \in \mathbb {N}$. For each instance, label all elements in $A^*_{i, j}$ as $a^*_1, \ldots , a^*_m$ and all elements in $B^*_{i, j}$ as $b^*_1, \ldots , b^*_n$ such that $b^*_1$ and $b^*_n$ have degree 1.

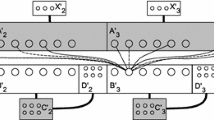
The construction makes extensive use of the path gadget depicted in Fig. 5. Observe that if $G'$ contains a path gadget as an induced subgraph, while the remainder of the graph only connects to its terminals $\textsc {in}^0$ and $\textsc {in}^1$, then any Hamiltonian cycle in $G'$ traverses the path gadget in one of the two ways depicted in Fig. 5. We create an instance $G'$ of Directed Hamiltonian Cycle that acts as the logical or of the inputs. A sketch of $G'$ is shown in Fig. 6.

• 1. First of all construct $\sqrt{t}$ groups of m path gadgets each. Refer to these groups as $A_i$, for $i \in [\sqrt{t}]$, and label the gadgets within group $A_i$ as $a_1^i, \ldots , a_m^i$. Let the union of all created sets $A_i$ be named A. Similarly, construct $\sqrt{t}$ groups of n path gadgets each. Refer to these groups as $B_j$, for $j \in [\sqrt{t}]$, and label the gadgets within group $B_j$ as $b_1^j, \ldots , b_n^j$. Let B be the union of all $B_j$ for $j \in [\sqrt{t}]$.

• 2. For every input instance $X_{i, j}$, for each edge $\{a^*_k, b^*_\ell \}$ in $G_{i, j}$ with $k \in [m]$, $\ell \in [n]$, add an arc from $\textsc {in}^0$ of $a_k^i$ to $\textsc {in}^1$ of $b_\ell ^j$ and an arc from $\textsc {in}^0$ of $b_\ell ^j$ to $\textsc {in}^1$ of $a_k^i$.

If some $G_{i, j}$ has a Hamiltonian $s-t$ path, it can be mimicked by the combination of $A_i$ and $B_j$, where for each vertex in $G_{i, j}$ we traverse its path gadget in $G'$, following Path 1. The following construction steps are needed to ensure that such a path can be extended to a Hamiltonian cycle in $G'$.

• 3. Add an arc from the $\textsc {in}^1$ terminal of $a_\ell ^i$ to the $\textsc {in}^0$ terminal of $a_{\ell +1}^i$ for all $\ell \in [m-1]$ and all $i \in [\sqrt{t}]$. Similarly add an arc from the $\textsc {in}^1$ terminal of $b_\ell ^i$ to the $\textsc {in}^0$ terminal of $b_{\ell +1}^i$ for all $\ell \in [n-1]$ and all $i \in [\sqrt{t}]$.

• 4. Add a vertex $\textsc {start}$ and a vertex $\textsc {end}$ and the arc $(\textsc {end},\textsc {start})$.

• 5. Let $r := \sqrt{t}-1$, add 2r tuples of vertices, $x_i, y_i$ for $i \in [2r]$ and connect $\textsc {start}$ to $x_1$. Furthermore, add the arcs $(y_i, x_{i+1})$ for $i \in [2r-1]$.

• 6. For $i \le r$ we add arcs from $x_i$ to the $\textsc {in}^0$ terminal of the gadgets $a_1^j, j\in [\sqrt{t}]$. Furthermore we add an arc from $\textsc {in}^1$ of $a_m^j$ to $y_i$ for all $j\in [\sqrt{t}]$ and $i \in [r]$. When $i > r$ add arcs from $x_i$ to the $\textsc {in}^0$ terminal of $b_1^j$ for $j \in [\sqrt{t}]$ and connect $\textsc {in}^1$ of $b_n^j$ to $y_i$.

• 7. Add a vertex $\textsc {next}$ and the arc $(y_{2r}, \textsc {next})$ and an arc from $\textsc {next}$ to the $\textsc {in}^1$ terminal of all gadgets $b_1^j$ for $j \in [\sqrt{t}]$.

• 8. Furthermore, add arcs from $\textsc {in}^0$ of all gadgets $b_n^j$ to $\textsc {end}$ for $j \in [\sqrt{t}]$. So for each $B_j$, exactly one vertex has an outgoing arc to $\textsc {end}$ and one has an incoming arc from $\textsc {next}$.$\square$

Fig. 6

The general structure of the created graph, when given four inputs with $n = 3$ and $m = 4$. The gray lines (

) show a Hamiltonian cycle in the constructed graph. The black lines (

) show arcs of $G'$ that are not used in the cycle. For readability, from the arcs between groups $A_i$ and $B_j$, only those between $A_1$ and $B_1$ have been drawn

This completes the construction of $G'$. In order to prove that the created graph $G'$ acts as a logical or of the given input instances, we first establish a number of auxiliary lemmas.

Lemma 4

Any Hamiltonian cycle in $G'$ traverses any path gadget in $G'$ via directed Path 0 or Path 1, as shown in Fig. 5.

Proof

Any Hamiltonian cycle in $G'$ should visit the center vertex of the path gadget. Since $\textsc {in}^0$ and $\textsc {in}^1$ are its only two neighbors in $G'$, the only option is to visit them consecutively. Path 0 and Path 1 are the only two options to do this. $\square$

Lemma 5

When any Hamiltonian cycle in $G'$ enters path gadget $a_1^i$ at $\textsc {in}_0$ for some $i~\in ~[\sqrt{t}]$, the cycle then visits the gadgets $a_2^i, a_3^i, \ldots , a_m^i$ in order without visiting other vertices in between. Similarly, if any Hamiltonian cycle in $G'$ enters path gadget $b_1^j$ at $\textsc {in}_0$, the cycle then visits the gadgets $b_2^j, b_3^j,\ldots ,b_n^j$ in order without visiting other vertices in between.

Proof

Consider a Hamiltonian cycle in $G'$ that enters path gadget $a_1^i$ at $\textsc {in}_0$. By Lemma 4 the cycle follows Path 0 and continues to the $\textsc {in}^1$ terminal of the path gadget. Since that terminal has only one out-neighbor outside the gadget, which leads to the $\textsc {in}_0$ terminal of $a_2^i$, it follows that the cycle continues to that path gadget. As the adjacency structure around the other path gadgets is similar, the lemma follows by repeating this argument. The proof when entering group $B_j$ at the vertex $\textsc {in}_0$ of $b_1^j$ is equivalent. $\square$

In Step 6 we create a selection mechanism that leaves one group in A and one in B unvisited. The following lemma formalizes this idea.

Lemma 6

Let C be a directed Hamiltonian cycle in $G'$, such that its first arc is $(\textsc {start},x_1)$. There are indices $i^*, j^* \in [\sqrt{t}]$ such that subpath $C_{x_1, y_{2r}}$ of the cycle between $x_1$ and $y_{2r}$ contains exactly the vertices

$$\begin{aligned} \overline{A_{i^*}} \cup \overline{B_{j^*}} \cup \{x_i, y_i \mid i \in [2r]\} \end{aligned}$$

where $\overline{A_{i^*}}$ contains all vertices of all gadgets in $A_i$ for $i \ne i^*$, and similarly $\overline{B_{j^*}}$ contains all vertices of all gadgets in $B_j$ for $j \ne j^*$.

Proof

We will first show that when the cycle reaches any $x_i$ for $i \in [r]$, it traverses exactly one group $A_\ell$ with $\ell \in [r+1]$ and continues to $y_j$ and $x_{j+1}$ for some $j \in [r]$, without visiting other vertices in between. Similarly, when the cycle reaches any $x_i$ for $r < i \le 2r$, it traverses exactly one group $B_\ell$ with $\ell \in [r+1]$ and continues to $y_j$ for some $r < j \le 2r$. For $j < 2r$, the cycle then continues to $x_{j+1}$, for $j = 2r$ the cycle reached $y_{2r}$, which is the last vertex of this subpath.

By Step 6 in the construction, all outgoing arcs of any $x_i$ for $i \in [r]$ lead to gadgets $a_1^\ell$ for some $\ell \in [\sqrt{t}]$. So for any $x_i$ in the cycle there must be a unique $\ell \in [\sqrt{t}]$ such that the arc from $x_i$ to the $\textsc {in}^0$ terminal of $a_1^{\ell }$ is in C. By Lemma 5 the cycle visits all vertices in $A_\ell$, and no other vertices, before reaching gadget $a_m^{\ell }$, which is traversed by Path 0 to get to $\textsc {in}^1$ of this gadget. The only neighbors of $\textsc {in}^1$ of gadget $a_m^{\ell }$ lying outside this gadget are of type $y_j$ for $j \in [r]$. As such, the cycle must visit some $y_j$ next, and its only outgoing arc goes to $x_{j+1}$.

The proof for $i > r$ is similar. As such, visiting $x_i$ for $i \in [r]$ results in visiting all vertices of exactly one group in A before continuing via $y_j$ to some $x_{j+1}$ without visiting any vertices in between. Visiting $x_i$ for $r < i \le 2r$ results in visiting all vertices of exactly one group in B and returning via $y_j$ to either the end of the subpath ($j=2r$) or some $x_{j+1}$.

Every vertex $x_i$ for $i \in [2r]$ must be visited by C, it remains to show that it is visited in subpath $C_{x_1, y_{2r}}$. Suppose there exists an $x_i$ for $i \in [2r]$ such that $x_i$ is not visited in the subpath from $x_1$ to $y_{2r}$. As we have seen above, visiting some $x_i$ results in visiting all vertices in some group in A or B, continued by visiting some $y_j$ for $j \in [2r]$. Note that no other vertices are visited in between. Therefore, if $x_i$ is not in subpath $C_{x_1, y_{2r}}$, then the corresponding $y_j$ is not in the subpath $C_{x_1, y_{2r}}$ either. This implies $j \ne 2r$ and thus the next vertex in the cycle is $x_{j+1}$. So, for $x_i$ not in subpath $C_{x_1, y_{2r}}$, one can find a new vertex $x_{j+1}$ (where $j+1 \ne i$), such that $x_{j+1}$ is also not in subpath $C_{x_1, y_{2r}}$. Note that we can not create a loop, by visiting a vertex $x_i$ seen earlier, as this would not yield a Hamiltonian cycle in $G'$. For example, the vertex start would never be visited. This is however a contradiction since we only have finitely many vertices $x_i$.

Thus in subpath $C_{x_1, y_{2r}}$, exactly r groups of A are visited and exactly r groups of B are visited, and no other vertices than specified. As $r = \sqrt{t}-1$, this leaves exactly one group $A_{i^*}$ and one group $B_{j^*}$ unvisited in $C_{x_1, y_{2r}}$. $\square$

Lemma 7

Let C be a Hamiltonian cycle in $G'$, such that its first arc is $(\textsc {start}, x_1)$. Let $i^*$ and $j^*$ satisfy the conditions of Lemma 6. Then cycle C enters gadget $b_1^{j^*}$ at terminal $\textsc {in}^1$ and visits $b_1^{j^*}$ before $b_n^{j^*}$. Moreover, the subpath of the cycle $C_{b_1^{j^*}, b_n^{j^*}}$ between terminal $\textsc {in}^1$ of $b_1^{j^*}$ and $\textsc {in}^0$ of $b_n^{j^*}$ (inclusive) contains all vertices of the gadgets in $A_{i^*}$ and $B_{j^*}$ and no others.

Proof

Vertex $\textsc {next}$ is visited directly after $y_{2r}$, since it is the only out-neighbor of $y_{2r}$. Furthermore, the arc from $\textsc {next}$ to gadget $b_1^\ell$ must be in the cycle for some $\ell \in [\sqrt{t}]$, since $\textsc {next}$ only has outgoing arcs of this type. By Lemma 6, all gadgets in all $B_j$ for $j \ne j^*$ are visited in the path from $x_1$ to $y_{2r}$, and thus should not be visited after vertex $\textsc {next}$. Therefore, the arc from $\textsc {next}$ to the $\textsc {in}^1$ terminal of gadget $b_1^{j^*}$ is in the cycle, which also implies that $b_1^{j^*}$ is visited before $b_n^{j^*}$.

It is easy to see that $(\textsc {end},\textsc {start})$ is the last arc in C. By considering the incoming arcs of $\textsc {end}$ it follows that some arc from terminal $\textsc {in}^0$ of $b_n^{\ell }$ to $\textsc {end}$ for $\ell \in [\sqrt{t}]$ is in the cycle. Since the vertices in gadgets $b_n^\ell$ for $\ell \ne j^*$ are already visited in $C_{x_1, y_{2r}}$ by Lemma 6, it follows that $(b_n^{j^*}, \textsc {end})$ is in C.

By Lemma 6, none of the terminals of gadgets in $A_{i^*}$ and $B_{j^*}$ are visited in the subpath $C_{x_1,y_{2r}}$ or equivalently in the subpath $C_{\textsc {start},\textsc {next}}$. Since C is a Hamiltonian cycle these vertices must therefore be visited in $C_{\textsc {next},\textsc {start}}$, which is equivalent to saying that $C_{b_1^{j^*},b_n^{j^*}}$ must contain all vertices in $A_{i^*}\cup B_{j^*}$. It is easy to see that this subpath cannot contain any other vertices, as all other vertices are present in $C_{\textsc {start},\textsc {next}}$ or $C_{\textsc {end},\textsc {start}}$. $\square$

Using the lemmas above, we can now prove that $G'$ has a Hamiltonian cycle if and only if one of the input instances has a Hamiltonian path.

Lemma 8

Graph $G'$ has a directed Hamiltonian cycle if and only if at least one of the instances $X_{i,j}$ has a Hamiltonian $s-t$-path.

Proof

($\Leftarrow$) Suppose $G'$ has a Hamiltonian cycle C. By Lemma 7 there exist indices $i^*,~j^*~\in ~[\sqrt{t}]$ such that the subpath of C from gadget $b_1^{j^*}$ to $b_n^{j^*}$ visits exactly the gadgets in $A_{i^*} \cup B_{j^*}$. Since gadget $b_1^{j^*}$ is entered at terminal $\textsc {in}^1$, it is easy to see that all gadgets in $A_{i^*} \cup B_{j^*}$ are traversed using Path 1. We now construct a Hamiltonian path P for instance $X_{i^*,j^*}$. Let $\{a^*_k(i^*,j^*), b^*_\ell (i^*,j^*)\} \in P$ if the arc from $\textsc {in}^0$ of $a_k^{i^*}$ to $\textsc {in}^1$ of $b_\ell ^{j^*}$ is in C. Similarly let $\{b^*_\ell (i^*,j^*), a^*_k(i^*,j^*)\} \in P$ if the arc from $\textsc {in}^0$ of $b_\ell ^{j^*}$ to $\textsc {in}^1$ of $a_k^{i^*}$ is in C, where $k \in [m]$ and $\ell \in [n]$. Using that every gadget is visited exactly once via Path 1 in C, we see that C is a Hamiltonian path.

($\Rightarrow$) Suppose $X_{i^*,j^*}$ has a Hamiltonian $s-t$ path P. Then we create a Hamiltonian cycle C as follows. For each vertex $a^*_\ell$ from instance $X_{i^*,j^*}$ in P we add Path 1 in path gadget $a_\ell ^{i^*}$ to C and for each vertex $b^*_\ell$ we add Path 1 in path gadget $b_\ell ^{j^*}$ to C. Let P be ordered such that $b^*_1$ is its first vertex. Now if $a^*_k$ is followed by $b^*_\ell$ in P, the arc from terminal $\textsc {in}^0$ of $a^{i^*}_k$ to $\textsc {in}^1$ of $b^{j^*}_\ell$ is added to C. Similarly, if a vertex $b_\ell ^*$ is followed by $a_k^*$ in P, the arc from terminal $\textsc {in}^0$ of $b^{j^*}_\ell$ to $\textsc {in}^1$ of $a^{i^*}_k$ will be added to C. Now the subpath $C_{b_1^{j^*},b_n^{j^*}}$ contains all terminals in all gadgets in $A_{i^*} \cup B_{j^*}$.

From $b_n^{j^*}$ the cycle goes to $\textsc {end}$, then to $\textsc {start}$ and to $x_1$. To visit all groups $A_i$ for $i \ne i^*$ and $B_j$ for $j \ne j^*$, do the following.

• From $x_i$ where $1\le i < i^*$, the cycle continues to gadgets $a_1^i$, then to $a_2^i, a_3^i, \ldots , a_m^i$ following Path 0, and continues to $y_i$, followed by $x_{i+1}$.

• From $x_i$ where $i^* \le i \le r$ it goes to $a_1^{i+1},a_2^{i+1},\ldots , a_m^{i+1}$ and continues with $y_i,x_{i+1}$.

• Similarly, from $x_{i+r}$ where $1 \le i < j^*$, go through gadgets $b_1^i,\ldots , b_n^i$ and continue to $y_{i+r}$ and $x_{i+r+1}$.

• From $x_{i+r}$ where $j^* \le i \le r$, go to gadgets $b_1^{i+1},\ldots ,b_n^{i+1}$ and continue to $y_{i+r}$, for $i \ne 2r$ then add the arc $(y_{i+r},x_{i+r+1})$.

From $y_{2r}$, continue to $\textsc {next}$, after which the arc $(\textsc {next}, b_1^{j^*})$ closes the cycle. By definition, no vertex is visited twice, so it remains to check that every vertex of $G'$ is in the cycle. For vertices $\textsc {start}, \textsc {next}, \textsc {end}$ and all vertices $x_i$ and $y_i$ this is obvious. All vertices in $A_i$ and $B_j$ where $i \ne i^*$ and $j \ne j^*$ are in the cycle between some $x_\ell$ and $y_\ell$. All vertices in $A_{i^*}$ and $B_{j^*}$ are visited since P was a Hamiltonian path on these vertices. $\square$

The number of vertices of $G'$ is

$$\begin{aligned} 3(m+n)\sqrt{t}+4(\sqrt{t}-1) + 3 = O(\sqrt{t} \cdot (m+n)) = O(\sqrt{t} \cdot \max |X_{i,j}|). \end{aligned}$$

By Lemma 8 the construction is a degree-2 cross-composition from Hamiltonian $s-t$ paths in bipartite graphs to Directed Hamiltonian cycle parameterized by the number of vertices, proving the generalized kernel lower bound for the directed problem. Karp [20] gave a polynomial-time reduction that, given an n-vertex directed graph G, produces an undirected graph $G'$ with 3n vertices such that G has a directed Hamiltonian cycle if and only if $G'$ has a Hamiltonian cycle. This is a linear parameter transformation from Directed Hamiltonian cycle to Hamiltonian cycle. Since linear-parameter transformations transfer lower bounds [3, 4], we conclude that (Directed) Hamiltonian cycle does not have a generalized kernel of size $O(n^{2-\varepsilon })$ for any $\varepsilon > 0$. $\square$

5 Dominating Set

In this section we discuss the Dominating Set problem and its variants. Dom et al. [9] proved several kernelization lower bounds for the variant Red-Blue Dominating Set, which is the variant on bipartite (red/blue colored) graphs in which the goal is to dominate all the blue vertices by selecting a small subset of red vertices. Using ideas from their kernel lower bounds for the parameterization by either the number of red or the number of blue vertices, we prove sparsification lower bounds for (Connected) Dominating Set. Since we parameterize by the number of vertices, the same lower bounds apply to the dual problems Nonblocker [6] and Max Leaf Spanning Tree.

We will prove these sparsification lower bounds using a degree-2 cross-composition, starting from a variation of the Colored Red-Blue Dominating Set problem (Col-RBDS) as described by Dom et al.in [9].

We will think of the vertices in set $R_i$ as having color i. Hence the question is whether there is a set $S \subseteq R$ containing exactly one vertex of each color, such that every vertex in B is adjacent to at least one vertex in S.

Lemma 9

eq-Col-RBDS is NP-complete.

Proof

Dom et al.[9] proved the NP-completeness of Colored RBDS without the constraint that all color sets have equal size. The NP-completeness for the equal-sized version follows from the fact that we may repeatedly add isolated vertices to classes $R_i$ that are too small, without changing the answer. $\square$

Using this result, we can now give a degree-2 cross-composition and prove the following.

Theorem 4

(Connected) Dominating Set, Nonblocker, and Max Leaf Spanning Tree parameterized by the number of vertices n do not have a generalized kernel of size $O(n^{2-\varepsilon })$ for any $\varepsilon > 0$, unless $\mathsf {NP \subseteq coNP/poly}$.

Proof

A graph has a nonblocker of size k if and only if it has a dominating set of size $n-k$. Furthermore, the Maximum Leaf Spanning Tree problem is strongly related to Connected Dominating Set. The internal vertices of any spanning tree form a connected dominating set. Conversely, any connected dominating set contains a subtree spanning the dominating set, which – by the domination property – can be greedily extended to a spanning tree for the entire graph in which the remaining vertices are leaves. Hence a graph has a connected dominating set of size at most k if and only if it has a spanning tree with at least $n-k$ leaves. Therefore we will show this result for (Connected) Dominating Set only.

Define a polynomial equivalence relation $\mathscr {R}$ on instances of eq-Col-RBDS by first of all letting all instances where there is a vertex in B of degree 0 be in the same class, note that these are always no-instances. Otherwise, let two instances $(G = (R\cup B),k)$ and $(G' = (R'\cup B'),k')$ of eq-Col-RBDS be equivalent if $|R| = |R'|$ , $|B| = |B'|$ and $k = k'$. It is easy to see that $\mathscr {R}$ indeed is a polynomial equivalence relation.

Suppose we are given t instances of eq-Col-RBDS, such that $\sqrt{t},\log {\sqrt{t}} \in \mathbb {N}$ and such that all given instances are in the same equivalence class of $\mathscr {R}$. Let $t':= \sqrt{t}$. If these instances are from the class where B contains a vertex of degree 0, output a constant size no-instance.

Otherwise, label the given instances as $X_{i,j}$ with $i,j \in [t']$. Let instance $X_{i,j}$ have graph $G_{i,j}$, which is bipartite with vertex set $R^*_{i,j} \cup B^*_{i,j}$. Let $|R^*_{i,j}| = m$ and $|B^*_{i,j}|~=~n$ and let $R^*_{i,j}$ be partitioned into k color classes $R^{*p}_{i,j}$ for all $i,j \in [{t'}]$ and $p \in [k]$. Label all vertices in $R^{*p}_{i,j}$ as $r^*_{p,q}(i,j)$ with $p \in [k]$ and $q \in [m/k]$, which means that this vertex is the q’th vertex of color p from instance $X_{i,j}$. Label vertices in $B^*_{i,j}$ as $b^*_1(i,j),\ldots ,b^*_n(i,j)$ arbitrarily. We now create an instance $(G,k')$ for Dominating Set using the following steps. A sketch of G can be found in Fig. 7.

• 1. Add vertices $r_{p,q}^i$ for $p \in [k], q \in [m/k]$ and $i \in [t']$. The dominating set problem does not use colored instances, however we will remember the color of these vertices for simplicity. Let vertex $r_{p,q}^i$ have color p, for $i \in [t']$, $q \in [m/k]$ and $p \in [k]$. Define $R_i := \{r_{p,q}^i \mid p \in [k], q\in [m/k]\}$ and let $R := \bigcup _{i\in [t']} R_i$. Give every set $R_i$ a unique identifier $\textsc {{id}}(R_i)$, which is a subset of $K := 2+k+\log t'$ numbers in the range [2K].

• 2. Add vertices $b_\ell ^j$ for $\ell \in [n]$ and $j \in [t']$. Define $B_j$ and B as $B_j := \{b_\ell ^j \mid \ell \in [n]\}$ and $B := \bigcup _{j \in [t']} B_j$.

• 3. For $p\in [k]$, $q \in [m/k]$, $\ell \in [n]$, and $i,j \in [t']$, add an edge between $r^i_{p,q}$ and $b^j_\ell$ if $r^*_{p,q}(i,j)$ is adjacent to $b^*_\ell (i,j)$ in instance $X_{i,j}$. This ensures that the graph induced by $R_i \cup B_j$ is exactly $G_{i,j}$ and the coloring of vertices in $R_i$ matches the coloring of $R^*_{i,j}$.

• 4. Add vertices $s'$ and s and add the edge $\{s', s\}$. Furthermore, add edges between s and all vertices in R. The degree-1 vertex $s'$ ensures there is a minimum dominating set containing s, which covers all vertices in R “for free”.

• 5. In a similar way as given by Dom et al. in [9], for every pair of colors $(c_1,c_2)~\in ~\{1,\ldots ,k\}~\times ~\{1,\ldots ,k\}$ with $c_1 \ne c_2$ we add a vertex set $W_{(c_1,c_2)}~=~\{w_1^{(c_1,c_2)},\ldots ,w_{2K}^{(c_1,c_2)}\}$.

  For $x \in [2K]$ and $i \in [t']$ connect $w_x^{(c_1,c_2)}$ to all vertices of color $c_1$ in $R_i$ if $x \in \textsc {{id}}(R_i)$, otherwise connect $w_x^{(c_1,c_2)}$ to all vertices of color $c_2$ in $R_i$. This construction is used to choose which $R_i$ is part of a solvable input instance $X_{ij}$ for some $j \in [t']$. This idea is formalized in Lemmas 12 and 13.

• 6. Then, add $\log {t'}$ triangles, with vertices $\{t_\ell ^0, t_\ell ^1, t_\ell ^2\}$ for $\ell \in [ \log {t'}]$. Connect $t_\ell ^0$ to all vertices in $B_j$ if the $\ell$’th bit of j equals 0, connect $t_\ell ^1$ to all vertices in $B_j$ if the $\ell$’th bit of j equals 1. Define T to be the union of all these triangles. By choosing exactly one of the vertices $t_\ell ^0$ or $t_\ell ^1$ in a dominating set for each $\ell$, all groups $B_j$ except one are dominated automatically. The non-dominated one should then be part of a solvable input instance.

• 7. Finally, add the edges $\{\{s,t_\ell ^i\} \mid \ell \in [\log t'], i \in \{0,1\}\}$. This step ensures that every vertex in T that is contained in the dominating set has s as a neighbor in the dominating set, which implies that there is always a minimum dominating set that is connected.$\square$

This concludes the construction of the graph G. We define $k' := k + 1 + \log t'$, which fully determines the output instance $(G, k')$ of the cross-composition. We develop a series of lemmas to analyze the properties of the constructed graph G.

Lemma 10

If G has a dominating set D, then it also has a dominating set $D'$ of size at most |D| that does not contain any vertices from B.

Proof

Suppose we are given a minimum dominating set D of G, where vertex $v \in B$ is present. In any dominating set, s or $s'$ must be present. If $s'$ is present and s is not, we replace $s'$ by vertex s, and still obtain a valid dominating set of the same size. As such, all vertices in R are now dominated by s. Vertices $t^0_\ell$ and $t^1_\ell$ with $\ell \in [\log {t'}]$ are dominated by s. Since $t^2_\ell$ only has neighbors $t^1_\ell$ and $t^0_\ell$, at least one of these three vertices is present in D for every $\ell \in [\log t']$, hereby every vertex in T has a neighbor in D.

Since B is an independent set in G, the vertex v does not dominate other vertices in B. Since the polynomial equivalence relation ensures that there are no isolated vertices in B, vertex v has at least one neighbor u in R. We can safely replace v by u to obtain a valid dominating set that has the same size as D and contains fewer vertices from B. The lemma follows by repeating this argument. $\square$

Lemma 11

Any dominating set of G of size at most $k+1+\log t'$ contains at least $1+\log {t'}$ vertices from $\{s,s'\} \cup \{t^0_\ell ,t^1_\ell ,t^2_\ell \mid \ell \in [\log t']\}$ and thus contains at most k vertices from R.

Proof

In a dominating set D of G, at least $\log t'$ vertices are needed from T, since $t^2_\ell$ only has neighbors $t^1_\ell$ and $t^0_\ell$, so one of these vertices must be in D for each $\ell \in [\log t']$. Furthermore at least one of the vertices $s'$ or s must be present, therefore there are $1+\log {t'}$ vertices in the set that are not from R. $\square$

Lemma 12

Any dominating set of G of size at most $k+1+\log t'$ uses exactly one vertex of each color from R.

Proof

Lemma 11 implies that a dominating set of size at most $k+1+\log t'$ uses at most k vertices from R, and hence at most k colors. In the other direction, suppose a dominating set of G of size at most $k+1+\log t'$ uses less than k colors from R. If at most $k-2$ colors are used, there must be two colors $c_1$ and $c_2$ that are not present in the set. However, this implies that all 2K vertices in $W_{(c_1,c_2)}$ are not dominated by vertices in R and must therefore be in the set. This contradicts the maximum size of the dominating set, since $K = k + 2 + \log t'$. So, we are left with the possibility of using $k-1$ colors. Consider some color $c_1$ that was not used. Look at another color $c_2$ that is used exactly once, such a color exists by Lemma 11. Suppose the vertex of color $c_2$ in the dominating set was from set $R_i$ for some $i \in [{t'}]$. Then for any $x \in \textsc {{id}}(R_i)$ we have that $w_x^{(c_1,c_2)}$ is not connected to any vertex in the dominating set and therefore must be in the dominating set itself. Since $\textsc {{id}}(R_i)$ contains K numbers, there are K vertices that are not dominated by R, which contradicts the maximum size of the dominating set. $\square$

Lemma 13

For any dominating set D of G of size at most $k+1+\log t'$, there exists $i \in [{t'}]$ such that all vertices in $D \cap R$ are contained in set $R_i$.

Proof

Suppose there exist two vertices $u,v \in D$ such that $u \in R_i$ and $v \in R_j$ for some $i \ne j$. By Lemma 12, u and v have different colors and are the only vertices in D with that color. Suppose u has color $c_u$ and v has color $c_v$. Since $R_i \ne R_j$, there exists $x \in [2K]$ such that $x \notin \textsc {{id}}(R_i)$ and $x \in \textsc {{id}}(R_j)$. By Step 5 of the construction, this means that none of the neighbors of vertex $w_x^{(c_u, c_v)}$ are contained in the dominating set. By lemmas 11 and 12, none of the vertices of W is contained in D, implying $w_x^{(c_u,c_v)}\notin D$. Therefore D is not a dominating set of G, which is a contradiction. $\square$

Fig. 7

A sketch of G, where $t'=2$, $m=6$ , $n=5$ and $k=2$. Thereby K should be 5 and $W_{(c_1,c_2)}$ should contain 10 vertices. In this example we show the constructed graph when choosing $K=1$ for simplicity. We use the two colors $c_1$ and $c_2$, corresponding to white and black in the figure. Edges from R to B are left out for simplicity

Using the previous lemmas, we obtain:

Lemma 14

• 1. If there is an input $X_{i^*,j^*}$ that has a col-RBDS of size k, then G has a connected dominating set of size $k+1+\log {t'}$.

• 2. If G has a (not necessarily connected) dominating set of size $k+1+\log t'$, then some input $X_{i^*,j^*}$ has a col-RBDS of size k.

Proof

(1)   Let $X_{i^*,j^*}$ have a colored RBDS D of size at most k. We construct a dominating set $D'$ of G in the following way. For any vertex $r^*_{p,q}$ in D, add vertex $r^{i^*}_{p,q}$ to $D'$. Furthermore add the vertex s to $D'$. Then add vertex $t_\ell ^0$ to $D'$ if the $\ell$’th bit of $j^*$ is 1, add vertex $t_\ell ^1$ otherwise. Now $s'$ is dominated and all vertices in R have neighbor s in $D'$. All vertices in $B_{j^*}$ are dominated by the vertices in the dominating set from $R_{i^*}$, since D was a col-RBDS of $X_{i^*,j^*}$. All vertices in $B_j$ for $j \ne j^*$ have neighbor $t_\ell ^0$ or $t_\ell ^1$ in $D'$ for some $\ell \in [\log {t'}]$, since the bit representation of j must differ from the one of $j^*$ at some position. It now follows from Step 6 of the construction that all vertices in $B_j$ are adjacent to a vertex in the dominating set.

It remains to verify that all vertices in W have a neighbor in $D'$. Consider $w_x^{(c_1,c_2)}$ for $x \in [2K]$ and distinct $c_1,c_2\in [k]$. If $x \in \textsc {{id}}(R_{i^*})$, then this vertex is connected to all vertices of color $c_1$ in $R_{i^*}$ and exactly one of them is contained in $D'$. If $x \notin \textsc {{id}}(R_{i^*})$, the vertex $w_x^{(c_1,c_2)}$ is connected to all vertices of color $c_2$ in $R_{i^*}$ and again one vertex of this color in $R_{i^*}$ is contained in $D'$. So $D'$ is a dominating set of G and it is easy to verify that $|D'|=k + 1 + \log t'$. Furthermore, $D'$ is constructed in such a way that it is connected. We can show this by proving that every vertex in $D'$ is a neighbor of s, since we chose s in D. Vertices in $D'\cap R$ and $D'\cap T$ are neighbors of s, by Steps 4 and 7 of the construction of G. The vertex $s'$ and vertices from W and B are not contained in $D'$. Thus, $D'$ is a connected dominating set.

(2) Let $D'$ be a dominating set of G of size at most $k + 1 + \log t'$. Using Lemma 10 we modify $D'$ such that it chooses no vertices from B, without increasing its size. By Lemma 12 and 13, $D'$ contains exactly k vertices from R, all from the same $R_{i^*}$ for some $i^*$ and all of different colors. $D'$ has size at most $k + 1 + \log t$ of which k are contained in R and one in $\{s,s'\}$. Combined with the fact that for any $\ell \in [\log t']$ vertex $t^2_\ell$ has $t^1_\ell$ and $t^0_\ell$ as its only two neighbors, it follows that exactly one of these three vertices is contained in $D'$ for all $\ell$. Therefore $D'$ contains at most one of the vertices $t_\ell ^0$ or $t_\ell ^1$ for every $\ell \in [\log t']$.

We can now define $x_\ell \in \{0,1\}$ for $\ell \in [\log {t'}]$, such that $t_\ell ^{x_\ell } \notin D'$ for all $\ell \in [\log {t'}]$. Consider the index $j^* \in [t]$ given by the binary representation $[x_1\,x_2\,\ldots \,x_{\log {t'}}]_2$. It follows from the bit representation of $j^*$ that the vertices in $B_{j^*}$ are not adjacent to any of the vertices in $D'\cap T$. Since vertices in $B_{j^*}$ are only adjacent to vertices in R and vertices of T, it follows that every vertex in $B_{j^*}$ has a neighbor in R that is in $D'$. This implies that every vertex in $B_{j^*}$ has a neighbor in $D'\cap R_{i^*}$. Since $G[R_{i^*} \cup B_{j^*}]$ is isomorphic to the graph of instance $X_{i^*,j^*}$, it follows that $X_{i^*,j^*}$ has a col-RBDS of size at most k, which are exactly the vertices in $D'\cap R_{i^*}$. $\square$

Given t instances, the graph G constructed above has $n~\cdot ~{t'} + m~\cdot ~{t'} + 2 + 3~\cdot ~\log {t'} + 2\left( {\begin{array}{c}k\\ 2\end{array}}\right) \cdot 2K = O(\sqrt{t} \max |X_{i,j}|^2)$ vertices. It is straightforward to construct G in polynomial time. It follows from Lemma 14 that G has a dominating set of size $k'=k + 1 + \log t'$, if and only if one of the input instances has a col-RBDS of size k. Furthermore, G has a connected dominating set of size $k+1+\log t'$ if and only if one of the input instances has a col-RBDS of size k. Therefore we have given a degree-2 cross-composition to (Connected) Dominating Set. Using Theorem 1 it follows that Dominating Set and Connected Dominating Set do not have a generalized kernel of size $O(n^{2-\varepsilon })$ for any $\varepsilon > 0$, unless $\mathsf {NP \subseteq coNP/poly}$. $\square$

Just as the sparsification lower bounds for Vertex Cover that were presented by Dell and van Melkebeek [8] had implications for the parameterization by the solution size k, Theorem 4 has implications for the kernelization complexity of k-Nonblocker and k-Max Leaf. Since the solution size k never exceeds the number of vertices in this problem, a kernel with $O(k^{2-\varepsilon })$ edges would give a nontrivial sparsification, contradicting Theorem 4. Hence our results show that the existing linear-vertex kernels for k-Nonblocker [6] and k-Max Leaf [11] cannot be improved to $O(k^{2-\varepsilon })$ edges unless $\mathsf {NP \subseteq coNP/poly}$.

6 d-Hypergraph 2-Colorability and d-NAE-SAT

The goal of this section is to give a nontrivial sparsification algorithm for nae-sat and prove a matching lower bound. For ease of presentation, we start by analyzing the closely related hypergraph 2-colorability problem. Recall that a hypergraph consists of a vertex set V and a set E of hyperedges; each hyperedge $e \in E$ is a subset of V. A 2-coloring of a hypergraph is a function $c :V \rightarrow \{1,2\}$; such a coloring is proper if there is no hyperedge whose vertices all obtain the same color. We will use d-Hypergraph 2-Colorability to refer to the setting where hyperedges have size at most d. The corresponding decision problem asks, given a hypergraph, whether it is 2-colorable.

A hypergraph is critically 3-chromatic if it is not 2-colorable, but for every hyperedge e there is a 2-coloring that is proper on all hyperedges except e. Lovász used linear algebra to prove an upper bound of $\left( {\begin{array}{c}n\\ d-1\end{array}}\right)$ on the number of hyperedges in a critically 3-chromatic d-uniform hypergraph on n vertices. His proof can be made algorithmic and leads to a nontrivial compression for d-Hypergraph 2-Colorability, as shown in the following theorem.

Theorem 5

d-Hypergraph 2-Colorability parameterized by the number of vertices n has a kernel with $n^{d-1} + 1$ hyperedges that can be encoded in $O(n^{d-1}~\cdot ~d~\cdot ~\log n)$ bits.

Proof

Suppose we are given a hypergraph with vertex set V and hyperedges E, where each hyperedge contains at most d vertices. We show how to reduce the number of hyperedges without changing the 2-colorability status. Let $E_r \subseteq E$ denote the set of edges in E that contain exactly r vertices. For each $E_r$ we construct a set $E'_r \subseteq E_r$ of representative hyperedges. Enumerate the edges in $E_r$ as $e^r_1,\ldots ,e^r_k$. We construct a (0, 1)-matrix $M_r$ with $N:=\left( {\begin{array}{c}n\\ r-1\end{array}}\right)$ rows and k columns. Consider all possible subsets $A_1,\ldots ,A_N$ of size $r-1$ of the set of vertices V. Define the elements $m_{i,j}$ for $i\in N$ and $j \in k$ of $M_r$ as follows.

$$\begin{aligned} m_{i,j} := \left\{ \begin{array}{ll} 1 &{} \quad \text{ if } A_i \subseteq e^r_j; \\ 0 &{} \quad \text{ otherwise. } \end{array} \right. \end{aligned}$$

Using Gaussian elimination, compute a basis B of the columns of this matrix, which is a subset of the columns that span the column space of $M_r$. Let $E'_r$ contain edge $e^r_i$ if the i’th column of $M_r$ is contained in B, and define $E' := \bigcup _{r \in [d]} E'_r$, which forms the kernel. Using a lemma due to Lovász [21], we can prove that $E'$ preserves the 2-colorability status. $\square$

Lemma 15

([21]) Let H be an r-uniform hypergraph with edges $E_1,\ldots ,E_m$. Let $\alpha _1,\ldots ,\alpha _m$ be real numbers such that for every $(r-1)$-element subset A of V(H),

$$\begin{aligned} \sum _{E_i \supset A} \alpha _i = 0. \end{aligned}$$

Then for every partition $\{V_1,V_2\}$ of V(H) the following holds:

$$\begin{aligned} \sum _{E_i\subseteq V_1} \alpha _i = (-1)^r \sum _{E_i \subseteq V_2} \alpha _i. \end{aligned}$$

Now we can prove the correctness of the presented kernel.

Lemma 16

(V, E) has a proper 2-coloring $\Leftrightarrow$ $(V,E')$ has a proper 2-coloring.

Proof

($\Rightarrow$) Clearly, if (V, E) has a proper 2-coloring, then the same coloring is proper for the subhypergraph $(V,E')$ since $E' \subseteq E$.

($\Leftarrow$) Now suppose $(V,E')$ has a proper 2-coloring. We will show that for each $r \in [d]$, no edge of $E_r$ is monochromatic under this coloring. All hyperedges contained in $E'_r$ are 2-colored by definition. Suppose there exists $r \in [d]$, such that $E_r$ contains a monochromatic hyperedge. Let $E_r = e^r_1,\ldots ,e^r_k$ and let $e_{i^*}$ be a hyperedge in $E_r$ whose vertices all receive the same color.

By reordering the matrix $M_r$, we may assume that the basis B of $M_r$ contains the first $\ell$ columns, thus $i^* > \ell$. Let $\mathbf {m}_i$ denote the i’th column of $M_r$. Since $\mathbf {m}_{i^*}$ is not contained in the basis, there exist coefficients $\alpha _1,\ldots ,\alpha _\ell$ such that

$$\begin{aligned} \sum _{i=1}^\ell \alpha _i\cdot \mathbf {m}_i = \mathbf {m}_{i^*}. \end{aligned}$$

For $i \in [k]$, define:

$$\begin{aligned} \beta _i := \left\{ \begin{array}{lll} \alpha _i &{} \quad \text{ if } i \le \ell ;\\ -1 &{} \quad \text{ if } i=i^*; \\ 0 &{} \quad \text{ otherwise. } \end{array} \right. \end{aligned}$$

From this definition of $\beta$ it follows that

$$\begin{aligned} \sum _{i=1}^{k} \beta _i\cdot \mathbf {m}_i = \sum _{i=1}^\ell \alpha _i\cdot \mathbf {m}_i - \mathbf {m}_{i^*}= \mathbf {0}. \end{aligned}$$

Let $A_j$ be any size $(r-1)$-subset of V. Since $m_{i,j} = 1$ exactly when $e_i \supseteq A_j$, and 0 otherwise, we have:

$$\begin{aligned} \sum _{e_i \supset A_j} \beta _i = \sum _{i=1}^{k} \beta _i m_{i,j} = 0. \end{aligned}$$

By Lemma 15 we obtain that for any partitioning $V_1 \cup V_2$ of the vertices in V,

$$\begin{aligned} \sum _{e_i\subseteq V_1} \beta _i = (-1)^r \sum _{e_i \subseteq V_2} \beta _i. \end{aligned}$$

(1)

Consider however the partitioning $(V_1, V_2)$ given by the 2-coloring of the vertices. Then every edge $e_i \in E'_r$ contains at least one vertex of each color and is thereby not fully contained in $V_1$ or $V_2$. As such, these edges contribute 0 to both sides of the equation. The edge $e_{i^*}$ is the only remaining edge with a non-zero coefficient and by assumption, it is contained entirely within one color class. Without loss of generality, let $e_{i^*} \subseteq V_1$. But then $\sum _{e_i\subseteq V_1} \beta _i = -1$ while $(-1)^r \sum _{e_i \subseteq V_2} \beta _i = 0$, which contradicts (1). $\square$

To bound the size of the kernel, consider the matrix $M_r$ for $r \in [d]$. Its rank is bounded by the minimum of its number of rows and columns, which is at most $\left( {\begin{array}{c}n\\ r-1\end{array}}\right)$. As such, we get $|E'_r|~\le ~\mathrm {rank}(M_r)~\le \left( {\begin{array}{c}n\\ r-1\end{array}}\right)$ for each $r \in [d]$, implying that $|E'|~\le ~\sum _{r=1}^d \left( {\begin{array}{c}n\\ r-1\end{array}}\right) \le n^{d-1}+1$. In the last step we use the fact that $\sum _{r=2}^{d} \left( {\begin{array}{c}n\\ r-1\end{array}}\right) = \sum _{i=1}^{d-1} \left( {\begin{array}{c}n\\ i\end{array}}\right) \le n^{d-1}$, which follows from the fact that the left-hand counts nonempty subsets of [n] of size at most $d-1$, and the right-hand counts tuples of size $d-1$ over [n]. Since each nonempty subset can be extended to a unique tuple by repeating an element, the number of nonempty subsets of size at most $d-1$ is at most the number of $(d-1)$-tuples.

We conclude that $E'$ contains at most $n^{d-1} + 1$ hyperedges. Since a hyperedge consists of at most d vertices, the kernel can be encoded in $O(n^{d-1}\cdot d \cdot \log {n})$ bits. $\square$

By a folklore reduction, Theorem 5 gives a sparsification for nae-sat. Consider an instance of d-nae-sat, which is a conjunction of clauses of size at most d over variables $x_1, \ldots , x_n$. The formula gives rise to a hypergraph on vertex set $\{x_i, \lnot x_i \mid i \in [n]\}$ containing one hyperedge per clause, whose vertices correspond to the literals in the clause. When additionally adding n hyperedges $\{x_i, \lnot x_i\}$ for $i \in [n]$, it is easy to see that the resulting hypergraph is 2-colorable if and only if there is a NAE-satisfying assignment to the formula. The maximum size of a hyperedge matches the maximum size of a clause and the number of created vertices is twice the number of variables. We can therefore sparsify an n-variable instance of d-nae-sat in the following way: reduce it to a d-hypergraph with $n' := 2n$ vertices and apply the kernelization algorithm of Theorem 5. It is easy to verify that restricting the formula to the representative hyperedges in the kernel gives an equisatisfiable formula containing $(n')^{d-1} + 1 \in O(2^{d-1} n^{d-1})$ clauses, giving a sparsification for nae-sat. As mentioned in the introduction, the existence of a linear-parameter transformation [19] from d-cnf-sat to ($d+1$)-nae-sat also implies a sparsification lower bound for d-nae-sat, using the results of Dell and van Melkebeek [8]. Hence we obtain the following theorem.

Theorem 6

For every fixed $d \ge 4$, the d-nae-sat problem parameterized by the number of variables n has a kernel with $O(n^{d-1})$ clauses that can be encoded in $O(n^{d-1} \cdot \log n)$ bits, but admits no generalized kernel of size $O(n^{d-1-\varepsilon })$ for $\varepsilon > 0$ unless $\mathsf {NP \subseteq coNP/poly}$.

7 Conclusion

We have added several classic graph problems to a growing list of problems for which non-trivial polynomial-time sparsification is provably impossible under the assumption that $\mathsf {NP} \nsubseteq \mathsf {coNP}/\mathsf {poly}$. Our results for (Connected) Dominating Set proved that the linear-vertex kernels with ${\varTheta }(k^2)$ edges for k-Nonblocker and k-Max Leaf Spanning Tree cannot be improved to $O(k^{2-\varepsilon })$ edges unless $\mathsf {NP \subseteq coNP/poly}$.

The graph problems for which we proved sparsification lower bounds can be defined in terms of vertices: the 4-Coloring problem asks for a partition of the vertex set into four independent sets, Dominating Set asks for a dominating subset of vertices, and Hamiltonian Cycle asks for a permutation of the vertices that forms a cycle. In contrast, not much is known concerning sparsification lower bounds for problems whose solution is an edge subset of possibly quadratic size. For example, no sparsification lower bounds are known for well-studied problems such as Max Cut, Cluster Editing, or Feedback Arc Set in Tournaments. Difficulties arise when attempting to mimic our lower bound constructions for such edge-based problems. Our constructions all embed t instances into a $2 \times \sqrt{t}$ table, using each combination of a cell in the top row and bottom row to embed one input. For problems defined in terms of edge subsets, it becomes difficult to “turn off” the contribution of edges that are incident on vertices that do not belong to the two cells that correspond to a yes-instance among the inputs to the or-construction. This could be interpreted as evidence that edge-based problems such as Max Cut might admit non-trivial polynomial sparsification. We have not been able to answer this question in either direction, and leave it as an open problem. For completeness, we point out that Karp’s reduction [20] from Vertex Cover to Feedback Arc Set (which only doubles the number of vertices) implies, using existing bounds for Vertex Cover [8], that Feedback Arc Set does not have a compression of size $O(n^{2-\varepsilon })$ unless $\mathsf {NP \subseteq coNP/poly}$.

Another problem whose compression remains elusive is 3-Coloring. In several settings (cf. [12]), the optimal kernel size matches the size of minimal obstructions in a problem-specific partial order. This is the case for d-nae-sat, whose kernel with $O(n^{d-1})$ clauses matches the fact that critically 3-chromatic d-uniform hypergraphs have at most $O(n^{d-1})$ hyperedges. Following this line of reasoning, it is tempting to conjecture that 3-Coloring does not admit subquadratic compressions: there are critically 4-chromatic graphs with ${\varTheta }(n^2)$ edges [23].

The kernel we have given for d-nae-sat is one of the first examples of non-trivial polynomial-time sparsification for general structures that are not planar or similarly guaranteed to be sparse. Obtaining non-trivial sparsification algorithms for other problems is an interesting challenge for future work. Are there natural problems defined on general graphs that admit subquadratic sparsification?