Internally coupled ears: mathematical structures and mechanisms underlying ICE

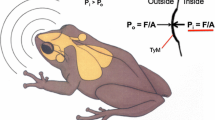
Abstract

In internally coupled ears (ICE), the displacement of one eardrum creates pressure waves that propagate through air-filled passages in the skull, causing a displacement of the opposing eardrum and vice versa. In this review, a thorough mathematical analysis of the membranes, passages, and propagating pressure waves reveals how internally coupled ears generate unique amplitude and temporal cues for sound localization. The magnitudes of both of these cues are directionally dependent. On the basis of the geometry of the interaural cavity and the elastic properties of the two eardrums confining it at both ends, the present paper reviews the mathematical theory underlying hearing through ICE and derives analytical expressions for eardrum vibrations as well as the pressures inside the internal passages, which ultimately lead to the emergence of highly directional hearing cues. The derived expressions enable one to explicitly see the influence of different parts of the system, e.g., the interaural cavity and the eardrum, on the internal coupling, and the frequency dependence of the coupling. The tympanic fundamental frequency segregates a low-frequency regime with constant time-difference magnification (time dilation factor) from a high-frequency domain with considerable amplitude magnification. By exploiting the physical properties of the coupling, we describe a concrete method to numerically estimate the eardrum’s fundamental frequency and damping solely through measurements taken from a live animal.

Appendix: Estimating the eardrum’s fundamental frequency and damping coefficient

The fundamental frequency $f_{0}$ and the damping coefficient $\alpha$ of the eardrum are important quantities to auditory performance. The former to partitioning the auditory landscape, the latter to determining the duration of transient response of the tympanum. How, then, can we determine them in the practice of experiment?

To detemine both, we need two quantities from experimentally measured tympanic vibration and hearing cues. As we see from Figs. 17 and 18, the maximum of the iLD as well as the frequency $f_*$ at which, for say sound-source directions $\theta = \pm 90^\circ$, the internal iTD equals the external ITD are experimentally accessible and near $f_0$.

We can analytically estimate the location of the iLD maximum and determine $f_*$ in terms of $f_{0}$ by using the properties of the membrane frequency response $\Lambda$ or, more specifically, $\Lambda$’s integral over the membrane surface $\Lambda _{{\mathrm {tot}}}$; cf. (77). An experimental recipe follows at the end of this appendix. $\Lambda _{{\mathrm {tot}}}$ has been defined as

$$\begin{aligned} \Lambda _{{\mathrm {tot}}}=\int _{S_{{\mathrm {mem}}}} \hbox {d}S \, \Lambda (r,\phi ) = \displaystyle \sum _{m,n}^{\infty } K_{\mathrm {mn}}/\Omega _{\mathrm {mn}} \end{aligned}$$

(91)

where

$$\begin{aligned} K_{\mathrm {mn}}= \frac{\left( \int u_{\mathrm {mn}}\right) ^2}{\rho _M d_M\int u_{\mathrm {mn}}^2}, \,\,\, \Omega _{\mathrm {mn}}= \left( \omega ^2-\omega ^2_{{\mathrm {mn}}}-2i\alpha \omega \right) .\quad \end{aligned}$$

(92)

We can now explicitly split $\Lambda _{{\mathrm {tot}}}$ into its real and imaginary parts,

$$\begin{aligned} \mathfrak {R}\{ \Lambda _{{\mathrm {tot}}}\}&=\displaystyle \sum _{m,n}^{\infty } K_{{\mathrm {mn}}}\left( \omega ^2{-}\omega ^2_{{\mathrm {mn}}}\right) /\left[ \left( \omega ^2 -\omega ^2_{{\mathrm {mn}}}\right) ^2{+}4\alpha ^2\omega ^2\right] , \end{aligned}$$

(93)

$$\begin{aligned} \mathfrak {I}\{ \Lambda _{{\mathrm {tot}}}\}&=\displaystyle \sum _{m,n}^{\infty } K_{{\mathrm {mn}}}2\alpha \omega /\left[ \left( \omega ^2-\omega ^2_{{\mathrm {mn}}}\right) ^2 +4\alpha ^2\omega ^2\right] . \end{aligned}$$

(94)

$\mathfrak {R}\{\Lambda _{{\mathrm {tot}}}\}$ and $\mathfrak {I}\{ \Lambda _{{\mathrm {tot}}}\}$ have been plotted for Gekko and Varanus in Fig. 12a, b, respectively. We see that for a certain frequency $f_*$, $\mathfrak {R}\{\Lambda _{{\mathrm {tot}}} \} =0$. In Sect. 4.5 we have also shown that exactly at $f=f_*$ the internal time difference iTD becomes equal to the interaural time difference ITD. Furthermore, it is possible to measure the corresponding iLD at $f_*$. Using the definition (89) of the membrane vibration–amplitude ratio at $f_*$ and recalling that $\left. \rho c^2kL \Lambda _{{\mathrm {tot}}} / V_{{\mathrm {cav}}}\right| _{f=f_*}=i\eta$, we obtain

$$\begin{aligned} \left. \mathrm {iLD}\right| _{f=f_*}&= 20\log _{10}\left| \frac{u^\mathrm {ave}_L}{u^\mathrm {ave}_0}\right| = 20\log _{10}\frac{1+\eta }{1-\eta }\nonumber \\ \Rightarrow \eta&=\frac{10^{\mathrm {iLD}/20}-1}{10^{\mathrm {iLD}/20}+1}. \end{aligned}$$

(95)

Thus, by measuring the iLD at $f_*$, we can calculate the imaginary part of the membrane frequency response as well. We should also note here that $\eta$ is a dimensionless quantity. The resulting nonlinear equations in $\alpha$ and $\omega _{{\mathrm {mn}}}$ are given by

$$\begin{aligned} \left. \mathfrak {R}\{ \Lambda _{{\mathrm {tot}}} \} \right| _{f=f_*}&= \displaystyle \sum _{m,n}^{\infty }\frac{K_{{\mathrm {mn}}} \left( \omega _*^2-\omega ^2_{{\mathrm {mn}}} \right) }{\left( \omega _*^2-\omega ^2_{{\mathrm {mn}}}\right) ^2 +4\alpha ^2\omega _*^2}=0 \end{aligned}$$

(96)

$$\begin{aligned} \left. \mathfrak {I}\{ \Lambda _{{\mathrm {tot}}} \} \right| _{f=f_*}&= \displaystyle \sum _{m,n}^{\infty } \frac{K_{{\mathrm {mn}}}2\alpha \omega _*}{ \left( \omega _*^2-\omega ^2_{{\mathrm {mn}}}\right) ^2 +4\alpha ^2\omega _*^2}=\frac{\eta V_{{\mathrm {cav}}}}{\rho c L\omega _*} \end{aligned}$$

(97)

where $\omega _*=2\pi f_*$. We have also used the fact that $k=\omega /c$. Given the above equations, the problem boils down to calculing $f_0=\omega _{11}/2\pi$ and $\alpha$ as the remaining eigenfrequencies are related to the fundamental eigenfrequency by $f_{{\mathrm {mn}}}/f_0=\omega _{{\mathrm {mn}}}/\omega _{11}=\mu _{{\mathrm {mn}}}/ \mu _{11}$. Here $\mu _{{\mathrm {mn}}}$ is the $n\mathrm {th}$ zero of the Bessel function $J_\kappa$; cf. (39).

Having determined $f_*$ as well as $\eta$ through the corresponding iLD based on membrane vibration amplitudes, it would be possible to use (96) and (97) to obtain estimates for $f_0$ and $\alpha$. This can be done by using standard iterative algorithms to find the roots of functions. A common example is the Newton–Raphson method (Ch. 5 Stoer and Bulirsch 2002). For a real-valued function f, in order to find an approximation for its roots $x:f(x)=0$ we start with an initial guess of $x_0$. A better approximation for x is then given by

$$\begin{aligned}&x_{1}=x_0-\frac{f(x_0)}{f^\prime (x_0)}\\&x_{n+1}=x_n-\frac{f(x_n)}{f^\prime (x_n)}. \end{aligned}$$

To find a root for a system of two equations $(x,y):g_{1}(x,y)=0,\ g_{2}(x,y)=0$ in two dimensions, we would instead need to calculate the appropriate Jacobian matrix,

$$\begin{aligned} \mathbb {J}=\begin{pmatrix} \frac{\partial g_{1}}{\partial x} &{} \frac{\partial g_{1}}{\partial y} \\ \frac{\partial g_{2}}{\partial x} &{} \frac{\partial g_{2}}{\partial y} \end{pmatrix}. \end{aligned}$$

The corresponding iteration rule is given by

$$\begin{aligned} \begin{pmatrix} x_{n+1}\\ y_{n+1} \end{pmatrix}= \begin{pmatrix} x_{n}\\ y_{n} \end{pmatrix}-\mathbb {J}^{-1} \begin{pmatrix} g_1(x_{n},y_{n})\\ g_2(x_{n},y_{n}) \end{pmatrix}. \end{aligned}$$

(98)

In dimensions higher than 2, it is more feasible to multiply both sides of (98) by $\mathbb {J}$ and to solve the resulting system. Since we only need to estimate two values, the inverse of the Jacobian can be easily calculated. The relevant variables for our numerical problem are $x=f_0$ and $y=\alpha$ and the corresponding equations are given by

$$\begin{aligned} g_1(f_0,\alpha )&=\left. \mathfrak {R}\{ \Lambda _{{\mathrm {tot}}} \} \right| _{f=f_*}=0 \end{aligned}$$

(99)

$$\begin{aligned} g_2(f_0,\alpha )&=\left. \mathfrak {I}\{ \Lambda _{{\mathrm {tot}}} \} \right| _{f=f_*}-\frac{\eta V_{{\mathrm {cav}}}}{\rho c L\omega _*}=0. \end{aligned}$$

(100)

The derivatives needed to calculate the Jacobian are given by

$$\begin{aligned} \frac{\partial \mathfrak {R}\{ \Lambda _{{\mathrm {tot}}} \}}{\partial f_0}&=\frac{2}{f_0}\displaystyle \sum _{m,n}^{\infty } \frac{K_{\mathrm {mn}}\omega ^2_{{\mathrm {mn}}} \left( \left( \omega _*^2-\omega ^2_{{\mathrm {mn}}}\right) ^2 -4\alpha ^2\omega _*^2\right) }{\left| \Omega ^*_{\mathrm {mn}}\right| ^4}\, \end{aligned}$$

(101)

$$\begin{aligned} \frac{\partial \mathfrak {R}\{ \Lambda _{{\mathrm {tot}}} \}}{\partial \alpha }&=8\alpha \omega ^2_*\displaystyle \sum _{m,n}^{\infty }\frac{K_{\mathrm {mn}} \left( \omega _*^2-\omega ^2_{{\mathrm {mn}}}\right) }{\left| \Omega ^*_{\mathrm {mn}}\right| ^4}, \end{aligned}$$

(102)

$$\begin{aligned} \frac{\partial \mathfrak {I}\{ \Lambda _{{\mathrm {tot}}} \}}{\partial f_0}&=\frac{8\alpha \omega _*}{f_0}\displaystyle \sum _{m,n}^{\infty }\frac{K_{{\mathrm {mn}}} \left( \omega _*^2-\omega ^2_{{\mathrm {mn}}}\right) \omega ^2_{{\mathrm {mn}}}}{\left| \Omega ^*_{\mathrm {mn}}\right| ^4}, \end{aligned}$$

(103)

$$\begin{aligned} \frac{\partial \mathfrak {I}\{ \Lambda _{{\mathrm {tot}}} \}}{\partial \alpha }&=2\omega _*\displaystyle \sum _{m,n}^{\infty }\frac{K_{\mathrm {mn}} \left( \left( \omega _*^2-\omega ^2_{{\mathrm {mn}}}\right) ^2{-}4\alpha ^2\omega _*^2\right) }{\left| \Omega ^*_{\mathrm {mn}}\right| ^4}. \end{aligned}$$

(104)

where $\Omega ^*_{\mathrm {mn}}= \left( \omega _*^2-\omega ^2_{{\mathrm {mn}}}-2i\alpha \omega _*\right)$. The Newton–Raphson method converges quadratically to the correct value of the root.

In order to simplify the estimation of the relevant parameters, it would be prudent to separate the dependence on the size of the membrane from terms that arise independently in the mathematical analysis. Specifically, we look at the coefficients $K_{{\mathrm {mn}}}$ as given by (92). Writing the integrals in the numerator and denominator explicitly we obtain

$$\begin{aligned} \int \hbox {d}S\ u_{\mathrm {mn}}&= \displaystyle \int ^{2\pi -\beta }_\beta \sin \kappa (\phi -\beta ) \, \hbox {d}\phi \displaystyle \int ^{a_{{\mathrm {tymp}}}}_0 r J_\kappa \left( \mu _{\mathrm {mn}} r\right) \, \hbox {d}r \nonumber \\&= \frac{1}{\kappa }\left[ 1-\cos m\pi \right] \displaystyle \int ^{a_{{\mathrm {tymp}}}}_0 r J_\kappa \left( \mu _{\mathrm {mn}} r\right) \, \hbox {d}r \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \mathrm{and}\nonumber \\&= \frac{a^2_{{\mathrm {tymp}}}}{\kappa }\left[ 1-\cos m\pi \right] \displaystyle \int ^1_0 \tilde{r} J_\kappa \left( a_{{\mathrm {tymp}}}\mu _{\mathrm {mn}} \tilde{r}\right) \, \hbox {d}\tilde{r}\nonumber \\ \int \hbox {d}S\ u_{\mathrm {mn}}^2&=\displaystyle \int ^{2\pi -\beta }_\beta \sin ^2 \kappa (\phi {-}\beta ) \, \hbox {d}\phi \displaystyle \int ^{a_{{\mathrm {tymp}}}}_0 r J^2_\kappa (\mu _{\mathrm {mn}} r) \, \hbox {d}r \nonumber \\&=(\pi -\beta ) \displaystyle \int ^{a_{{\mathrm {tymp}}}}_0 r J^2_\kappa (\mu _{\mathrm {mn}} r) \, \hbox {d}r \end{aligned}$$

(105)

$$\begin{aligned}&=(\pi -\beta )a^2_{{\mathrm {tymp}}} \displaystyle \int ^1_0 \tilde{r} J^2_\kappa \left( a_{{\mathrm {tymp}}}\mu _{\mathrm {mn}} \tilde{r}\right) \, \hbox {d}\tilde{r}\nonumber \end{aligned}$$

(106)

where $\tilde{r}=r/a_{{\mathrm {tymp}}}$. Recall that $a_{{\mathrm {tymp}}}\times \mu _{\mathrm {mn}}$ corresponds to the $n\mathrm {th}$ zero of $J_\kappa$. We have thus separated the geometrical parameter $a_{{\mathrm {tymp}}}$ from the Bessel integrals in (105) and (106). Furthermore, we see that the integral in (105) is nonzero (and equal to 2) only for odd values of m as $\cos m\pi =1$ for even m.

For $\kappa [m]=0.5\ m\pi /(\pi -\beta )$, $m=1,3,5,\ldots$, we can rewrite $K_{{\mathrm {mn}}}$

$$\begin{aligned} K_{{\mathrm {mn}}}&=\frac{16}{\pi ^2}\frac{{\mathscr {S}}_{{\mathrm {tymp}}}}{\rho _M d_M } \widetilde{K}_{\mathrm {mn}}, \nonumber \\ \widetilde{K}_{{\mathrm {mn}}}&=\frac{\left( \displaystyle \int ^1_0 \tilde{r} J_\kappa \left( a_{{\mathrm {tymp}}}\mu _{\mathrm {mn}} \tilde{r}\right) \, \hbox {d}\tilde{r}\right) ^2}{m^2\displaystyle \int ^1_0 \tilde{r} J^2_\kappa \left( a_{{\mathrm {tymp}}}\mu _{\mathrm {mn}} \tilde{r}\right) \, \hbox {d}\tilde{r}}. \end{aligned}$$

(107)

where ${{\mathscr {S}}_{{\mathrm {tymp}}}}=(\pi -\beta )a^2_{{\mathrm {tymp}}}$ is the surface area of the tympanum. The values of $\widetilde{K}_{{\mathrm {mn}}}$ for 20 modes are given in Table 3 and are arranged in a descending order of $K_{{\mathrm {mn}}}/\mu ^2_{{\mathrm {mn}}}$, which is the value of $\Lambda _{{\mathrm {tot}}}$ at $f=0$. The $\widetilde{K}_{{\mathrm {mn}}}$ are independent of the size of the membrane and depend only on the extracolumellar angle $\beta$.

Table 3 Numerical parameters needed for estimating $f_0$ and $\alpha$

1.1 Numerical calculations in experimental practice

In practice, we would need to choose an appropriate cutoff for the membrane eigenmodes. Ideally, we have to ensure that the last eigenmode has a frequency well above the hearing range of the animal. In order to test our method for the numerical estimation of $f_0$ and $\alpha$, we have started by performing simulations for Gekko and Varanus while using the first 70 membrane eigenmodes, with the 70th mode corresponding to an eigenfrequency of around 11.7 and 4.45 kHz for Gekko and Varanus, respectively;—well beyond the hearing range of either species. The estimated values of $f_*$ and $\eta$ are shown in Table 4. In a real-world experimental setup, these values would correspond to those estimated from measured membrane vibration amplitudes and phases.

Table 4 Estimated $f_*$ and $\eta$

We seek to test the accuracy of our method by assuming that the values calculated for 70 modes were obtained experimentally. In passing, “were” is meant to be a subjunctive. This way we can test the performance of the algorithm in case the experimenter only chooses a limited number of modes. To do so, we would first need initial guesses for $f_0$ and $\alpha$. For the fundamental frequency we can take $f_*$ itself as eyeballing the iTD plots tells us that the values are fairly close to each other; cf. Fig. 17a, b. Based on the behavior of the membrane response as shown in Fig. 14a, b, one can conclude that the system is overdamped for Gekko and underdamped for Varanus. The value of the damping in the former would be ${>}\omega _*/4$ and ${<}\omega _*/4$ in the latter.

Given an initial guess, we can calculate the values of $\mathfrak {R}\{\Lambda _{\mathrm {tot}}\}$ and $\mathfrak {I}\{\Lambda _{\mathrm {tot}}\}$ at these values of $f_0$ and $\alpha$ from Eqs. (96) and (97). The value of the Jacobian can similarly be calculated by plugging these values into Eqs. (101)–(104) along with the values of $\widetilde{K}_{\mathrm {mn}}$ given in Table 3. Thereafter one can iteratively use the Newton–Raphson method (98) until a suitable convergence is reached.

The simulation was performed for $N_{{\mathrm {modes}}}=1, 2, 5, 10, 15, 20$, and 25 modes. The results of the simulation are presented in Table 5. For both Gekko and Varanus, we see that with an increasing number of eigenmodes used, the values converge to the quantities defined in Table 2. The slower convergence and apparent oscillation in $\alpha$ for Gekko is due to the higher value of its damping, which causes a greater difference between $f_*$ and $f_0$. However, we must be careful while choosing initial guesses for Varanus as its lower damping results in a larger number of extrema and roots, and a simulation might converge to a point corresponding to a higher eigenmode. In practice, five modes are more than sufficient for good convergence in both $f_0$ and $\alpha$. As a side remark, we need to emphasize that the numbers behind the decimal point in Tables 4 and 5 are experimentally irrelevant but are there just to demonstrate the accuracy of the numerical procedure.

Table 5 Simulation results

In summary, and focusing on $f_{0}$, as a rule of thumb one can take the location of the minimum of the contralateral amplitude on the tonotopic axis or, equivalently, the maximum of the iLD or, if one likes $f_{*}$ as the fundamental frequency $f_{0}$, the error being at most 5 %. Determining the damping coefficient $\alpha$ is a bit more work. The procedure outlined in Eqs. (96)–(107) gives us a systematic method to approximate $\alpha$ from the membrane vibrations for an arbitrary number of modes. In Table 5, we see that assuming $f_{*}$ to be the fundamental frequency, which is equivalent to assuming $f_0=f_{*}$, gives us a value of $\alpha$ with an error of at most 5 %. Taking into account the second mode further reduces the error to within 1 %. In fact, for the case of a single mode, the expression for $\alpha$ can be written down explicitly by substituting $\omega _0=\omega _{11}=\omega _{*}$ in (97) giving us

$$\begin{aligned} \frac{K_{\mathrm {11}}}{2\alpha \omega _{*}}&=\frac{\eta V_{{\mathrm {cav}}}}{\rho c L\omega _*}. \end{aligned}$$

(108)

$$\begin{aligned} \Rightarrow \ \alpha&=\frac{ \rho c L K_{\mathrm {11}} }{2\eta V_{{\mathrm {cav}}}} =\frac{8\rho c L}{\pi ^2 V_{\mathrm {cav}}}\frac{{\mathscr {S}}_{\mathrm {tymp}}}{ \rho _M d_M}\frac{\widetilde{K}_{\mathrm {11}}}{\eta }. \end{aligned}$$

(109)

We thus have (109) as an expression for the membrane damping coefficient $\alpha$ given only the geometrical and material parameters (thickness and density) of the membrane and cavity and $\eta$—the iLD measurement at a given frequency.