Modeling convergent ON and OFF pathways in the early visual system

Abstract

For understanding the computation and function of single neurons in sensory systems, one needs to investigate how sensory stimuli are related to a neuron’s response and which biological mechanisms underlie this relationship. Mathematical models of the stimulus–response relationship have proved very useful in approaching these issues in a systematic, quantitative way. A starting point for many such analyses has been provided by phenomenological “linear–nonlinear” (LN) models, which comprise a linear filter followed by a static nonlinear transformation. The linear filter is often associated with the neuron’s receptive field. However, the structure of the receptive field is generally a result of inputs from many presynaptic neurons, which may form parallel signal processing pathways. In the retina, for example, certain ganglion cells receive excitatory inputs from ON-type as well as OFF-type bipolar cells. Recent experiments have shown that the convergence of these pathways leads to intriguing response characteristics that cannot be captured by a single linear filter. One approach to adjust the LN model to the biological circuit structure is to use multiple parallel filters that capture ON and OFF bipolar inputs. Here, we review these new developments in modeling neuronal responses in the early visual system and provide details about one particular technique for obtaining the required sets of parallel filters from experimental data.

1 1 Introduction

Assessing the relationship between the sensory stimulus and the neuronal responses and identifying the underlying biological processes are central goals in the study of sensory systems. One way of addressing these questions is by construction of suited model descriptions that aim at quantitatively mapping the stimulus-response relation while simultaneously capturing the relevant neuronal dynamics (Gerstner and Kistler 2002; Dayan and Abbott 2005; Herz et al. 2006).

Here, we will review recent developments for modeling the spiking activity of retinal ganglion cells in response to visual stimulation. These models extend the widely used LN model approach that aims at describing neural responses in terms of a linear filter and a subsequent nonlinear transformation. Recent experiments in the retina have shown that specific response features of certain types of neurons intimately rely on the convergence of parallel processing pathways, which are the result of synaptic inputs from both ON-type and OFF-type bipolar cells. This convergence of parallel pathways with markedly different stimulus-processing characteristics can be captured by models with several linear filters in parallel. Extending the LN model in such a way brings about new data-analytical challenges for obtaining the parameters from experiments. We will begin by revisiting single- and multi-filter LN models and different techniques for extracting their parameters from data. After reviewing applications of the LN model to the retina and summarizing recent related experimental findings, we will provide details about the fitting procedure for one particular multi-pathway model that captures the effects of convergent ON and OFF pathways on first-spike latencies.

2 2 The LN modeling approach

2.1 2.1 Single-filter models

Analyzing how sensory signals affect the spiking activity of a neuron requires a good description of the neuronal stimulus-response relationship. The linear-nonlinear (LN) model has proven to provide a successful and convenient framework in many cases (Hunter and Korenberg 1986; Sakai 1992; Meister and Berry 1999; Carandini et al. 2005; Schwartz et al. 2006). Its basic model structure, shown in Fig. 1a, consists of a single linear filter “L” that converts a stimulus s(x, t), which can depend on time t and spatial coordinates x, into the filter output y(t). The following nonlinear transformation “N” of y(t) into the response r(t) is instantaneous in time. Typically, r(t) is interpreted as the neuron’s membrane potential or as the instantaneous firing rate, i.e., the spike probability per unit time.

Fig. 1

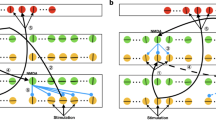
LN model and reverse correlation. a Structure of the LN model. In the first step, the stimulus s(x, t) is convolved with a linear filter to produce the filter output y(t). In the second step, this is nonlinearly transformed into the response r(t). b Structure of the multi-filter LN model. The stimulus s(x, t) is convolved with multiple linear filters in parallel, each resulting in a separate filter output y _n (t). The nonlinear transformation is now multi-dimensional; it takes all filter outputs as input and yields the response r(t). c Reverse correlation with a spatially homogeneous flicker stimulus. Light intensities of the stimulus are distributed according to a Gaussian distribution. For all measured spikes, the preceding stimulus segments are collected. The average of all these segments, the spike-triggered average, yields an estimate of the linear filter for the first stage of a single-filter LN model. d Reverse correlation with a stimulus composed of flickering stripes. Light intensities are again drawn from a Gaussian distribution. The stimulus segments that precede a spike have one temporal and one spatial dimension. The spike-triggered average can be plotted as a two-dimensional color plot, with blue denoting low light intensity (below mean level) and red denoting high light intensity (above mean level). It can again be interpreted as the filter of a single-filter LN model

A primary advantage of the LN model is the fact that obtaining the model parameters—the shape of the filter and the nonlinear transformation—can easily be achieved by a reverse correlation analysis with a stimulus that has a Gaussian (or otherwise spherically symmetric) distribution of intensity values (Chichilnisky 2001). In fact, the filter is then simply obtained as the spike-triggered average, i.e., the average of all stimulus segments that generated spikes. The nonlinearity can be subsequently determined, for example, by creating a histogram of the measured neuronal response over the computed filter output y(t). The ease of obtaining the model parameters from experimental data and their straightforward interpretation have made the LN model uniquely popular for modeling stimulus-response relationships of neurons in many sensory systems.

It is important to keep in mind, though, that the modeling of neuronal responses in terms of filters and transformations has an intrinsic phenomenological nature, aimed primarily at providing an accurate description of the signal-processing characteristics and less at capturing the individual biophysical processes that underlie the input-output relation. Nonetheless, this approach can be combined with biophysically inspired components, such as spike generation dynamics (Keat et al. 2001; Paninski et al. 2004; Pillow et al. 2005; Gollisch 2006) or gain control (Shapley and Victor 1978; Victor 1987; Berry et al. 1999). Explicitly incorporating parallel processing pathways for ON and OFF signals, as will be discussed below, represents a similar biologically inspired extension. Before diving into this topic, we review generic phenomenological approaches to multi-filter models.

2.2 2.2 Multi-filter models

Reducing a neuron’s receptive field to a single linear filter has proven too restrictive in many examples. A straightforward remedy is to replace the linear filter in the first model stage by a set of parallel linear filters. Correspondingly, the subsequent nonlinearity becomes a nonlinear function that takes as input all the filter outputs from the first stage and produces a single variable as the output (Fig. 1b). Similar to the single-filter LN model, this multi-filter model draws part of its appeal from the existence of simple and elegant techniques for parameter estimation from experiments. Statistical analysis techniques, such as the “neuronal modes” approach (Marmarelis 1989; Marmarelis and Orme 1993; French and Marmarelis 1995) and, in particular, spike-triggered covariance as a straightforward extension of the spike-triggered average (de Ruyter van Steveninck and Bialek 1988; Touryan et al. 2002; Schwartz et al. 2006) have proved expedient for promoting the applicability of these models in various scenarios.

In short, the spike-triggered covariance analysis is based on comparing the stimulus variance of the complete stimulus set of Gaussian white noise to the variance of the stimulus subset that elicited spikes (“spike-triggered stimulus ensemble”). Typically, the stimulus variance differs between these two ensembles along such stimulus dimensions to which the neuron is sensitive. In other words, the filters of the multi-filter LN model define the only special dimensions of the stimulus space; for all other, orthogonal stimulus dimensions, the original symmetry of the stimulus distribution is preserved, and the stimulus variance stays constant. The stimulus dimensions that do experience a change in variance can be determined from a principal component analysis of the spike-triggered stimulus ensemble. An example for this is given in the presentation of a specific data fitting technique below.

These relevant stimulus features can be selected as the filters of the multi-filter LN model. Once the filters are obtained from the spike-triggered covariance analysis, one may aim at assessing the nonlinearity from the data by measuring how the instantaneous firing rate (or the spike probability) depends on the momentary outputs of the filters. Depending on the amount of available data, however, this is feasible only for a small number of filters. A more detailed account of the spike-triggered covariance methodology can be found in Schwartz et al. [2006].

2.3 2.3 Alternatives to spike-triggered analyses

There have been a number of recent developments regarding alternatives to the spike-triggered analysis techniques for obtaining LN models and variants thereof. In particular, information theory provides a framework for extracting filters that capture maximal information about the neural response (Paninski 2003; Sharpee et al. 2004). Information theory can furthermore be used to combine spike-triggered average and spike-triggered covariance analyses into a single conjoint analysis (Pillow and Simoncelli 2006).

Another set of successful techniques is based on maximum-likelihood approaches (Paninski et al. 2004). This method has also proved quite useful for incorporating additional processing modules, such as neuronal refractoriness and after-spike currents (Paninski et al. 2004; Pillow et al. 2005). One advantage of these alternative spike-triggered methods is that they can be readily applied to more complex stimulus conditions, such as natural stimuli. These typically contain higher order correlations that distort the filters obtained from spike-triggered analyses, which necessitates significant correction procedures (Theunissen et al. 2001; Felsen et al. 2005; Touryan et al. 2005).

3 3 LN models of retinal ganglion cell responses

3.1 3.1 Single-filter models

The neural network of the retina has a long tradition as a system of investigation that combines excellent experimental accessibility and computational rigor in the applied models (Spekreijse 1969; Marmarelis and Naka 1972; Levick et al. 1983; Victor 1987; Sakai 1992; Meister and Berry 1999; Keat et al. 2001; van Hateren et al. 2002; Pillow et al. 2005). One of its principal advantages for studying neuronal network function is the fact that its inputs and outputs are under very good experimental control. The retina can be optically stimulated by projecting images onto its photoreceptor layer. The output of the retina are the spike trains of ganglion cells, whose axons form the optic nerve and transmit all visual information that is accessible to the rest of the brain. These output spike trains can be efficiently and reliably recorded from isolated pieces of retina placed on multi-electrode arrays (Meister et al. 1994; Segev et al. 2004).

LN models and spike-triggered analyses have long been established as standard tools for analyzing responses of retinal ganglion cells. Examples for spike-triggered averages of two ganglion cells are shown in Fig. 1c and d, for a purely temporal stimulus as well as a spatiotemporal stimulus with one spatial dimension, respectively. In the first case, the stimulus is a spatially homogeneous flicker; in the second case, it consists of flickering stripes. All light intensity values, for the full-field illumination as well as for individual stripes, were drawn independently from a Gaussian distribution around some intermediate gray illumination level.

The filters obtained from this spike-triggered average analysis can be used to characterize the response types of the neurons. For both cells shown here, the filters display a negative part close to time zero; on average, the light intensity decreased shortly before the spike occurred. This fact is generally used to classify the cells as OFF-type (Segev et al. 2006). But both cells also show pronounced ON characteristics preceding the OFF part of the filters, giving the filters a strongly biphasic (or triphasic) shape. In fact, the two cells, like many similar ones, respond with bursts of spikes to both step increases and decreases in light intensity, which gives them a signature of ON-OFF cells (Burkhardt et al. 1998). ON and OFF responses in the retina are mediated by activation of ON and OFF bipolar cells that respond to light intensity increases and decreases, respectively. ON-OFF ganglion cells appear to receive inputs through both these pathways (Werblin and Dowling 1969; de Monasterio 1978; Burkhardt et al. 1998; Greschner et al. 2006).

It has recently been shown that the characterization of ON-type and OFF-type filters is not completely static. This became apparent by the following experiment (Geffen et al. 2007): ganglion cells of the salamander retina were stimulated by flickering light in their receptive field center. Under stationary stimulus conditions, the reverse correlation revealed typical OFF-type filters for many neurons. For some of these, the filter characteristics changed, however, when a sudden shift of a visual pattern occurred in the periphery—similar to the global image shifts that accompany saccadic eye movements. In the ensuing about 100 ms after this shift, some of these ganglion cells yielded filters typical for ON-type cells; this means that, temporarily, the filter shapes were nearly inverted as compared to stationary conditions. As we will see below, these intriguing findings can be explained by specific filter models that capture contributions from the ON and OFF pathways in separate filters.

3.2 3.2 Multi-filter models

The dynamic changes between ON and OFF characteristics of ganglion cells motivated a model with explicit input from ON and OFF bipolar cells. Experimental support that this circuit structure is relevant for the observed phenomena came from pharmacological tests. To investigate the involvement of ON bipolar cells, the drug 2-amino-4-phosphono-butyrate (APB) can be applied to the retina. APB is known to block the synaptic input from photoreceptors to ON bipolar cells (Slaughter and Miller 1981; Yang 2004). Indeed, the effect of the drug was to abolish the occurrence of the ON characteristics after the peripheral shift (Geffen et al. 2007).

The modeling efforts thus aim at explaining the observed changes in response characteristics after a saccade while taking into account the experimental findings about the cellular pathways involved. The approach is to capture the effects of inputs from both ON and OFF bipolar cells to the ganglion cell by separate filters, one with typical OFF-type characteristics, the other a typical ON-type filter (Fig. 2). The two filter outputs are sent through separate rectifying nonlinearities, which are thought to arise at the bipolar-to-ganglion cell synapse. Finally, the two pathways are summed to yield the ganglion cell’s firing rate. The power of this two-pathway model lies in the fact that it can easily capture the differences in signal processing between the steady-state and the time right after a saccade. It turns out that only the strengths of the two pathways need to be adjusted; no changes in the shapes of the filters are required. Furthermore, there is good evidence for the biological mechanism of this change in the weighting of the two pathways. This effect is mediated by a wide-field amacrine cell, which is activated by the peripheral shift and sends inhibitory signals to the circuit of the receptive field center (Geffen et al. 2007).

Fig. 2

Diagram of a ganglion cell model with separate ON and OFF pathways. The stimulus is filtered by an ON-type and an OFF-type filter, and each filter output is separately rectified by a nonlinearity. Summation finally leads to the model prediction of the firing rate response. Figure adapted from Geffen et al. [2007] under the Creative Commons Attribution License

Separate inputs from ON and OFF pathways into specific ganglion cells have also been suggested by a generic investigation of multi-filter LN models under spatially homogeneous flicker stimulation (Fairhall et al. 2006). In this study, the modeling goal was not to match a specific circuitry, but to find good quantitative descriptions of the ganglion cell responses and to classify the cells according to the number and shapes of filters obtained. The approach was to apply a spike-triggered covariance analysis, and the resulting models capture the ganglion cell responses remarkably well; using tools from information theory, this study found that the models generally account for more than 80% of the information that is transmitted by the instantaneous firing rate.

Of course, the spike-triggered analysis does not automatically lead to an understanding of which features of the neuronal circuitry correspond to the obtained filters and nonlinearities in the model. In some cases, however, certain features of the resulting model structure can be explained in terms of the biological substrate. For some ganglion cells, for example, the obtained two-filter LN model can be understood as resulting from threshold-based spike generation mechanisms (Fairhall et al. 2006). In other cases—and more importantly for our present purpose—the two filters arise from a confluence of ON and OFF inputs (Fairhall et al. 2006; Geffen et al. 2007).

4 4 Spike timing at stimulus onsets

Most modeling approaches that we have discussed so far aim at capturing the (time-dependent) firing rate of a neuron under continuous, stationary stimulus conditions. Another fundamental stimulus paradigm is given by the sudden appearance of a visual image. In natural vision, such sudden stimulus onsets are caused by saccades, i.e. rapid shifts of the direction of gaze (Land 1999). The prominent temporal structure that saccades enforce on the natural stream of visual signals falling onto the eye makes the study of neuronal responses to stimulus onsets of obvious relevance.

Even for the simplest stimulus onsets—step increases and decreases of the light intensity with no spatial structure—one finds intriguing phenomena in the timing of spike events elicited in ON-OFF ganglion cells. In the turtle retina, specific ON-OFF ganglion cells have been shown to display peculiar spike patterns to steps in light intensity (Greschner et al. 2006; Thiel et al. 2006). Whereas the first spike after the change in light intensity was monotonically shifted to earlier times with increasing size of the intensity step, the timing of a second spike event had a non-monotonic dependence on step size, with the shortest timing occurring for intermediate changes in light intensity. To explain these response characteristics, models were employed that combine parallel ON and OFF pathways with feedback components and gain control. Both in the form of a phenomenological cascade model (Greschner et al. 2006) as well as in the form of a biophysical model of the retina network (Thiel et al. 2006), this allowed an accurate reproduction of the encountered response phenomena.

When the stimuli are enriched with a spatial structure, the potential of spike timing effects for transmitting detailed spatial information about the newly encountered image becomes apparent (Gollisch and Meister 2008). This was studied by measuring the first-spike latencies of ganglion cells in the salamander retina in response to flashed images. As shown in Fig. 3a, ganglion cells typically responded with a precisely timed burst of spikes. To assess the cells’ responses, the number of spikes in the burst (“spike count”) as well as the time from stimulus onset to the first spike (“latency”) were measured when a grating was presented with different spatial phases, so that the boundaries between the dark and light regions of the grating lay at different locations.

Fig. 3

Latency coding by retinal ganglion cells. a Visual stimulus and schematic response. The applied visual stimulus consists of gray illumination of intermediate intensity for 750 ms, followed by a spatial square-wave grating for 150 ms. The spatial period of the grating was about 660 µm on the retina. Retinal ganglion cells typically respond to the onset of the grating with a short burst of spikes. The response latency is the time between stimulus onset and the first spike; the spike count is the total number of spikes elicited by the stimulus (counted over the window of 0–220 ms after stimulus onset). b Tuning curves for spike count and latency for a sample ganglion cell (same as in Fig. 1d). For this cell, both spike count and latency varied systematically with the spatial phase of the grating. The error bars denote standard deviations, measured over many repeats of the same stimulus

Most interestingly for the present discussion, many cells reliably responded with a burst of spikes to all spatial phases of the grating. This included responses to stimuli that were completely reversed in polarity so that bright and dark regions of the image were exchanged. Moreover, the latency of the response shifted systematically with the spatial phase of the grating. Early responses were observed when dark bars of the grating fell onto the neuron’s spatial receptive field; bright bars caused late responses. This relation between spatial phase of the stimulus and response latency can be summarized in a tuning curve (Fig. 3b) and compared to the corresponding tuning in spike count. For most recorded neurons, the latency was much more strongly tuned and consequently contained more information about the spatial phase of the stimulus. Moreover, this information is available already with the first spike, thus providing a potential signal for very rapid visual processing (Potter and Levy 1969; Thorpe et al. 2001; Kirchner and Thorpe 2006).

Again, the responses are intimately connected to the convergence of ON and OFF inputs; when APB was used to block ON inputs, the observed response phenomena disappeared, and the neurons behaved like pure OFF-type cells (Gollisch and Meister 2008). In the following, we will first discuss a model structure that captures these latency-tuning effects and subsequently elaborate on how the model parameters are obtained from electrophysiological data.

5 5 Modeling first-spike latencies for ON-OFF ganglion cells

The following model approach is aimed at capturing specifically the first spike latency after the onset of a flashed stimulus. The potential for rapid information transmission by latencies warrants special efforts to model this response feature. As pharmacological experiments indicated the necessity of signals from ON and OFF bipolar cells, a key aspect of the modeling will be the use of parallel ON and OFF pathways that correspond to separate stimulus filters.

However, before plunging into modeling separate ON and OFF pathways, let us consider for comparison a model without this separation. This is essentially a single-filter LN model, but adjusted for modeling first-spike latencies, as shown in Fig. 4a: The stimulus s(x, t) is homogeneous gray illumination followed by a square-wave grating over the spatial coordinate x. The relevant linear filter here is the spatiotemporal receptive field of the neuron, obtained as the spike-triggered average (Fig. 1d). A single spatial dimension of the filter suffices because the grating stimulus s(x, t) varies in light intensity only along one direction.

Fig. 4

Modeling the response latencies of ON-OFF ganglion cells. a Single-filter model. The stimulus is a spatial square-wave grating that appears for 150 ms. To obtain the activation of the ganglion cell, this stimulus is convolved with a single spatiotemporal filter, which corresponds to the cell’s receptive field. After applying a half-wave rectification, which removes negative excursions of the activation, a threshold-criterion is applied to the activation curve. Upon first crossing of the threshold, the model neuron fires its first spike, which determines the latency. As the receptive field is measured in a separate experiment, the threshold value is the only free parameter and is optimized by a least squares fit to the latency tuning curve. b Resulting model fit from the single-filter model. The data are the same as in Fig. 3b. The model fails to predict threshold crossings for four of the eight stimuli. c Extension of the filter model to incorporate separate filters for the ON and OFF pathway. The receptive field is split up into an ON field and an OFF field. Each is taken as a spatiotemporal filter, and their outputs are rectified and then summed. The first spike is again determined by a threshold criterion. d Fit of the two-pathway model to the data. Spikes are predicted for all eight stimuli, but the quantitative fit of the tuning curve is poor. e Model with multiple spatially local ON and OFF filters. For both the ON and OFF field, each stripe, corresponding to a distinct location on the retina, is considered as a separate (temporal) filter. The filter outputs are all individually rectified and then summed. f Fit of the multi-filter model to the data, again after optimization of the threshold value. In contrast to the other two model versions, the multi-filter model results in an excellent fit of the latency data

The first step of the model is to convolve the stimulus with this spatiotemporal filter f(x, τ) to obtain the filter output y(t) :

$$y(t) = \int {{\rm{d}}x\int\limits_{ - \infty }^0 {{\rm{d}}\tau s(x,t + \tau ) \cdot f(x,\tau ).} } $$

We here use a notation with continuous time and space; in practical applications, both are often naturally discretized by using stimuli with a fixed temporal frame rate and a pixelated spatial stimulus. The integrals are then converted into sums over frames and pixels.

Next, the linear response signal y(t) is half-wave rectified to yield the activation signal a(t) :

$$a(t) = N(y(t)),$$

where

$$N(y) = \left\{ {\matrix{ y & {{\rm{for }}y > 0} \cr 0 & {{\rm{for }}y \le 0} \cr } } \right.$$

is a half-wave rectifying nonlinearity.

Finally, a threshold criterion is used to convert this activation into the occurrence of a spike. The spike time t _spike is thus given by the time when a(t) crosses a (positive) threshold value θ :

$$a({t_{{\rm{spike}}}}) = \theta {\rm{and}}a(t) < \theta {\rm{for}}t < {t_{{\rm{spike}}}}.$$

The threshold value θ must be positive, otherwise a(t) would be above threshold already at stimulus onset. Here as well as in the subsequently presented model versions, the value of the threshold is the only free parameter of the model and is optimized by a χ ² fit to the latency tuning curve. All filter shapes are determined from independent measurements as will be discussed in the next section. Note that the half-wave rectification is included in this particular model simply for analogy with the multi-filter model discussed below; it has no effect on predicting the latency because negative values of y(t) cannot cross threshold.

This model fails to explain the measured responses (Fig. 4b). The primary reason is simply that the model produces no spikes at all for several of the stimuli; if one grating leads to a strong positive activation a(t), then the inverted grating results in a negative a(t).

Let us therefore extend this model by including separate filters for the ON and OFF pathways. As shown in Fig. 4c, this is achieved by splitting up the receptive field f(x, τ) into two separate filters: the ON field f ^(ON)(x, τ) and the OFF field f ^(OFF)(x, τ). These two fields are normalized so that

$${f^{({\rm{ON}})}}(x,\tau ) + {f^{({\rm{OFF}})}}(x,\tau ) = f(x,\tau ).$$

The normalization ensures consistency with the measured spike-triggered average and fixes the relative strengths of the ON and OFF pathways.

For each field, we compute a filter output by convolution with the visual stimulus:

$${y^{{\rm{(ON)}}}}(t) = \int {{\rm{d}}x\int\limits_{ - \infty }^0 {{\rm{d}}\tau s(x,t + \tau ) \cdot {f^{{\rm{(ON)}}}}(x,\tau )} } $$

$${y^{{\rm{(OFF)}}}}(t) = \int {{\rm{d}}x\int\limits_{ - \infty }^0 {{\rm{d}}\tau s(x,t + \tau ) \cdot {f^{{\rm{(OFF)}}}}(x,\tau ).} } $$

Before y ^(ON)(t) and y ^(OFF)(t) are combined into a single activation function a(t), they are individually half-wave rectified so that

$$a(t) = N\left( {{y^{{\rm{(ON)}}}}(t)} \right) + N\left( {{y^{{\rm{(OFF)}}}}(t)} \right).$$

The resulting activation a(t) is supplied with a threshold criterion as before; the first spike is elicited when a(t) crosses the threshold value θ.

As anticipated, this model now produces spikes for all stimuli, but the tuning of the latency curve is not well reproduced quantitatively (Fig. 4d). From the perspective of the neuronal circuitry, a flaw of this model version is that it takes into account the partition of bipolar cells into ON and OFF type, but not their smaller receptive field sizes as compared to ganglion cells; both the ON and the OFF field are still integrated linearly over space.

We therefore extend the model to include rectification prior to the summation over space, (Fig. 4e). We partition the spatial dimension x into subfields of Δx ≈ 80 µm, which corresponds about to the size of bipolar receptive fields (Hare and Owen 1996; Baccus et al. 2008). For each subfield x _n , we consider a separate set of ON and OFF filters, f ^(ON) _n (τ) and f ^(OFF) _n (τ), so that we receive a collection of filter outputs from both the ON and OFF pathway:

$${y_n}^{{\rm{(ON)}}}(t) = \int\limits_{ - \infty }^0 {{\rm{d}}\tau s(n \cdot \Delta x,t + \tau ) \cdot {f_n}^{{\rm{(ON)}}}(\tau )} $$

$${y_n}^{{\rm{(OFF)}}}(t) = \int\limits_{ - \infty }^0 {{\rm{d}}\tau s(n \cdot \Delta x,t + \tau ) \cdot {f_n}^{{\rm{(OFF)}}}(\tau ).} $$

Now, each output from y ^(ON) _n (t) or y ^(OFF) _n (t) is individually half-wave rectified, and the activation function a(t) is thus given by

$$a(t) = \sum\limits_n {N\left( {{y_n}^{{\rm{(ON)}}}(t)} \right) + \sum\limits_n {N\left( {{y_n}^{{\rm{(OFF)}}}(t)} \right).} } $$

When the threshold value θ is again optimized according to a χ ² fit, we obtain a remarkably good fit to the tuning curve of the first spike latency (Fig. 4f). The primary challenge of this model lies, however, in obtaining its principal parameters, the shapes of the ON and OFF fields. We will now outline a method for dealing with this challenge.

6 6 Obtaining the filters for an ON-OFF multi-pathway model

6.1 6.1 ON and OFF filters for spatially homogeneous stimulation

To obtain the ON and OFF filters, we need to separate the receptive field into contributions from these two pathways. To explain this procedure, we will first consider the case of spatially homogeneous stimuli where only the temporal stimulus dimension needs to be considered. Several studies (Fairhall et al. 2006; Greschner et al. 2006; Geffen et al. 2007; Gollisch and Meister 2008) have pursued this separation with variants of the same basic technique, which we will also follow here. It makes use of the fact that the ON and OFF pathways are sensitive to stimuli that are nearly inverted with respect to each other. It follows that typically one of the pathways can be excited, not both simultaneously. This allows a classification of the spikes according to the pathway that was responsible for providing excitation.

As in the computation of the spike-triggered average (Fig. 1c), the analysis is based on an experiment with flickering illumination and begins with collecting the stimulus segments that led to spikes, the spike-triggered stimulus ensemble. The light intensities are drawn from a Gaussian distribution and, for simplicity, normalized to zero mean and unit variance.

As explained above, a useful starting point for obtaining multiple filters is the spike-triggered covariance analysis, which computes the principal components of the spike-triggered stimulus ensemble. For this analysis, it is often easiest to think of the stimulus segments as points (or vectors) in a high-dimensional space; 20-dimensional in the present example because we consider the stimulus intensities over the 20 frames prior to a spike. We can then calculate the covariance matrix of the distribution of these data points as

$$C(n,m) = {{\sum\nolimits_{{t_{{\rm{spike}}}}} {\left( {s({t_{{\rm{spike}}}} - n \cdot \Delta t) - {\rm{STA}}( - n \cdot \Delta t)} \right)} \cdot \left( {s({t_{{\rm{spike}}}} - m \cdot \Delta t) - {\rm{STA}}( - m \cdot \Delta t)} \right)} \over {{N_{{\rm{spikes}}}} - 1}},$$

where STA(t) is simply the spike-triggered average and Δt is the duration of the frame, here 15 ms. The principal components are obtained as the eigenvectors of this matrix.

Figure 5a shows a spectrum of eigenvalues obtained from such an analysis for the cell whose receptive field was shown in Fig. 1c. As the light intensities were normalized to unit variance, most eigenvalues cluster around unity. The corresponding eigenvectors denote directions in stimulus space along which the variance did not change between the complete stimulus ensemble and the spike-triggered stimulus ensemble; they are therefore considered as non-relevant stimulus directions. (Note that in other studies, one also finds examples where the covariance matrix of the complete stimulus ensemble was subtracted from the spike-triggered covariance matrix before the eigenvalues are calculated. This is equivalent to the present approach, but the non-relevant eigenvalues will then cluster around zero).

Fig. 5

Separation of contributions from ON and OFF pathways with spatially homogeneous flicker stimuli. a Eigenvalue spectrum obtained from a principal component analysis of the spike-triggered stimulus ensemble. Many eigenvalues lie near unity, indicative of stimulus structures that do not affect the occurrence of a spike. At the low and high ends of the spectrum, however, deviations of the eigenvalues from unity indicate relevant stimulus structures. b Principal components corresponding to the highest (PC1) and lowest (PC2) eigenvalue. For comparison, the spike-triggered average (STA) is shown by the dashed line. c Instantaneous firing rate of the neuron, depending on the projection of the preceding stimulus segment onto the principal components PC1 and PC2 and onto the spike-triggered average, respectively. d Scatter plot of the projections of the spike-triggered stimulus segments onto PC1 and PC2. e Instantaneous firing rate of the neuron depending on the projections of the stimulus onto PC1 and PC2. As compared to the scatter plot in d, this form of display takes into account that the presented stimuli lie more densely close to the center than in the periphery. The two-dimensional bins are chosen along a polar coordinate system so that in each radial direction, each bin contains the same number of data points. Therefore, the area covered by the bins increases with radial distance because the stimuli lie less dense in the periphery. For display clarity, the last bin in each radial direction is not drawn to its actual size—it would stretch out much further in the radial direction if it were to cover the area of all contributing data points. f Spike-triggered averages obtained separately for each cluster. The clusters are separated along the vertical zero-axis in d, and the spike-triggered stimulus segments are averaged for each cluster. The two resulting waveforms display shapes that are typical for ON and OFF filters, respectively. Note that the OFF filter has faster kinetics; it peaks around 30 ms closer to time zero than that the ON filter

The spectrum of eigenvalues could now be analyzed statistically to find those components that significantly differ from unity, for example by computing the distribution of eigenvalues for temporally shuffled spike trains (Rust et al. 2005; Schwartz et al. 2006). This allows a formal analysis of how many filters should be included in the multi-filter LN model. Here, however, we are only interested in finding those (one or two) stimulus dimensions that let us best distinguish between contributions from the ON and OFF pathways. Therefore, we simply focus on the highest and lowest eigenvalue of the spectrum, which furthermore allows us to easily automate the analysis.

Clearly, the largest eigenvalue sticks out from the rest. This is typical for the analyzed neurons with ON-OFF response characteristics. The large eigenvalue corresponds to the fact that two nearly opposing pathways contribute to the response, which makes the variance of the spike-triggered stimulus ensemble along this direction particularly large. Thus, if no such eigenvalue emerges from the analysis, it is unlikely that both ON and OFF pathways contribute strongly. The lowest eigenvalue also deviates substantially from unity and is thus a candidate for denoting a relevant stimulus structure. Because its value is smaller than unity, the spike-triggered stimulus ensemble is compressed along this stimulus component. In specific contexts, this has been associated with suppressive response pathways (Schwartz et al. 2002), but it can arise from various sources, such as the dynamics of spike generation (Fairhall et al. 2006).

The principal components PC1 and PC2, corresponding to these maximal and minimal eigenvalues, respectively, are shown in Fig. 5b. To assess the effect of these stimulus components on the neuron’s response, we can compute the instantaneous firing rate depending on the projection P(t) of a stimulus segment onto the principal component with a stimulus segment. This projection measures how strongly the component is represented in the stimulus, and it is computed for each stimulus segment {s(t − N · Δt), …, s(t)} as the dot-product with the principal components PC1(t) and PC2(t), for example:

$${P_1}(t) = \sum\limits_{n = - N}^0 {{\rm{PC}}1(n \cdot \Delta t) \cdot s(t + n \cdot \Delta t).} $$

The instantaneous firing rate is obtained as the spiking probability during one stimulus frame, divided by the duration of the frame. To calculate this, we count the number of spikes that the neuron fired during the final frame of the segment. The segments are then collected into bins according to the projection values. For each bin, the averages of the projection values and the neuronal response are calculated and plotted against each other as in Fig. 5c.

Most strikingly, for the present case, the firing rate for PC1 is “U-shaped”, which means that large positive projections and large negative projections both caused the cell to fire. This phenomenon becomes more evident when we take a look at the projections of all spike-triggered stimulus segments on both PC1 and PC2. When these projection values are displayed in a scatter plot, as in Fig. 5d, two clouds of data points become apparent. For almost all spikes, the projection onto PC2 was negative, but the projection onto PC1 could have either large positive or large negative values.

Another illustrative way of displaying this information is achieved by plotting the instantaneous firing rate as a function of both projection values, as in Fig. 5e. Here, the data are combined into bins with similar projections onto PC1 and PC2, respectively. For each bin, the firing rate is calculated as the average rate during the final stimulus frame of all stimulus segments in that bin. In contrast to the scatter plot of Fig. 5d, this form of display takes into account that, because of the Gaussian distribution of stimulus values, many more stimuli are presented near the center of the plots, where the projection values are close to zero, than in the periphery.

The scatter plot in Fig. 5d and the display of the firing rate in Fig. 5e show that the spike-triggered stimulus ensemble can be separated into two clusters. These two-dimensional displays reinforce the notion that two fundamentally different types of stimuli elicit spikes. Both PC1 and PC2 influence the shapes of the clusters, and it is likely that further stimulus components (corresponding to further eigenvalues of the spectrum shown in Fig. 5a) also contribute to separating the clusters.

Different techniques have been utilized to separate the clusters, such as a formal multi-dimensional cluster analysis (Geffen et al. 2007), a classification of the spike-triggered stimulus segments depending on whether they show an average intensity increase or decrease in a short window prior to the spike (Greschner et al. 2006), or a separation along the zero axis of the first principal component PC1 (Fairhall et al. 2006; Gollisch and Meister 2008). Here, we follow the latter approach, which yields a good separation of the clusters in many cases, owing to the pronounced U-shape of the firing rate dependence on the PC1 projection in Fig. 5c, where the firing rate drops down to zero when the projection is zero. We thus assign the stimulus segments to clusters depending on whether the projection onto PC1 was positive or negative. This approach allows us to easily automate this step in the analysis explained below. We then calculate the spike-triggered average for each cluster separately (Fig. 5f). Their shapes are not constrained to the space spanned by PC1 and PC2; the calculation is performed in the original full stimulus space. This takes into account that the two clusters may also differ along further stimulus dimensions. The reduction to the two dimensions PC1 and PC2 merely serves for separating the clusters.

The shapes of the two obtained filters, shown in Fig. 5f, can be interpreted as representing processing through ON and OFF bipolar cells, respectively. The strong biphasic nature of both these filters results from the fact that the spatially homogeneous stimulus not only excites receptive field centers of bipolar cells and ganglion cells, but also the inhibitory surround. The filtering characteristics of this surround are typically temporally delayed and inverted with respect to the center (ON-center cells have an OFF surround and vice versa). Their superposition thus yields the biphasic filter shape under activation of the whole space.

Of particular importance is the observation that the OFF filter has “faster kinetics”, i.e., its peaks are closer to time zero as compared to the ON filter. This means that activation of the OFF filter affects spike probability with a shorter latency—an observation that is of obvious importance for explaining the differences in latency for the flashed gratings. This was consistently observed in all cells in the salamander retina where the separation of ON and OFF contributions was possible. The likely cause is a delay in the processing of ON stimuli that results from the involvement of metabotropic receptors at the synapse between photoreceptors and ON bipolar cells (Ashmore and Copenhagen 1980; Yang 2004). Now that we have separated contributions from the ON and OFF pathway for spatially homogeneous stimuli and obtained two biologically plausible filters, let us consider the case where the stimulus includes spatial structure.

6.2 6.2 Spatially local ON and OFF filters

In order to extend the approach presented in the previous section to the identification of spatially local ON and OFF filters, we use data from experiments where the stimulus consisted of independently flickering stripes on the screen. As explained above, this stimulus can be applied to compute a spatiotemporal receptive field with one spatial dimension (Fig. 1d). The goal now is to obtain a separation of this spatiotemporal receptive field into the ON and OFF fields, as shown in Fig. 6a. The analysis follows the same path as for the spatially homogeneous stimulus, but is done for each stimulus stripe separately. However, a significant challenge arises from the fact that a given stripe of the stimulus is not solely responsible for generating the spikes—the influence of other stripes creates a background of activity, which for the purpose of the current analysis acts as noise.

Fig. 6

Separating the spatiotemporal field into ON and OFF fields. a Spatiotemporal receptive field and ON and OFF fields. The goal of the analysis shown in the following panels is to separate the receptive field into its contributions from ON and OFF pathways. This is done for each row of the receptive field separately (corresponding to specific locations on the retina). For the locations marked with 1, 2, and 3, the results are drawn in the three columns of the subsequent panels. b Eigenvalues of the principal component analyses. In each case, the highest eigenvalue is separated from the other eigenvalues, which cluster around unity. The lowest eigenvalue is hardly separated from the rest. c Principal components PC1 and PC2 together with the spike-triggered average STA (dashed line) for each of the three locations. d Instantaneous firing rates, depending on the projections of the stimulus onto PC1 and PC2. Although not as clear as in Fig. 5e, the plots still show two clusters of stimuli that lead to high firing rate at large positive and large negative projections onto PC1. e Filters obtained by separating the clusters along the vertical zero-axis in d and calculating the spike-triggered average separately for each cluster. Note that, in each case, the OFF filter has a shorter time-to-peak than the ON filter by about 30 ms. By combining all ON filters and all OFF filters into a two-dimensional color plot, the ON and OFF fields of panel a are obtained

As for the case of spatially homogeneous stimulation, the relevant stimulus structures are again obtained from a principal component analysis. The analysis is shown in Fig. 6b–e, for those three stripes that lie in the center of the spatial receptive field of the sample neuron. Each eigenvalue spectrum (Fig. 6b) displays one eigenvalue that is much larger than unity. Most of the other eigenvalues are close to unity so that other relevant stimulus structures appear to be largely covered by noise. Consequently, as shown in Fig. 6c, the principal component corresponding to the largest eigenvalue, PC1, has a similar shape as previously, whereas the principal component corresponding to the minimal eigenvalue, PC2, is often dominated by noise. As we had seen in the previous section, however, a single stimulus component can suffice to separate ON and OFF contributions.

Indeed, a plot of the instantaneous firing rate in the space of PC1 and PC2 (Fig. 6d) reveals that spikes appear primarily when the projection onto PC1 is either strongly positive or strongly negative. Thus, we can separate stimulus segments activating the ON and OFF pathway, respectively, by selecting for positive or negative projection onto PC1. The resulting spike-triggered averages for each cluster, shown in Fig. 6e, display similar differences in kinetics as for the case of spatially homogeneous stimulation (Fig. 5f); for each stimulus stripe, the peaks of the OFF filters are closer to time zero than those of the ON filters. Also, all filters show a mild, but systematic biphasic structure, evident by the slow tail of opposite polarity as compared to the main peak. The biphasic nature of the filter is less pronounced than in the case of spatially homogeneous stimulation; the inhibitory surround that is responsible for the delayed inverted peak in the filter is still activated for individual stripes of the stimulus, but proportionally less so as compared to the spatially homogeneous stimulation.

Note that it is important to revert to the original stimulus segments for calculating the spike-triggered averages separately for the two clusters. The fact that the obtained ON and OFF filters are not exact inversions of each other, but indeed show systematic differences in their timing, underscores the importance of stimulus structures beyond the first principal component. Note also that the sets of ON filters and OFF filters are very similar across different stripes despite the fact that these were analyzed independently. This supports the reliability of the method. The actual test for the performance of the obtained model, however, is how closely it fits the data of the latency tuning curve (Fig. 4f).

7 7 Discussion

Neuronal models that are based on a single linear filter in the first stage of processing have a long and successful history, in the form of the widely used LN model (Hunter and Korenberg 1986; Chichilnisky 2001; Baccus and Meister 2002) as well as in combination with more complex mechanisms for processing and spike generation after the filtering stage (Keat et al. 2001; Pillow et al. 2005; Gollisch 2006). When parallel processing pathways are relevant for the function of a neuron, these single-filter models may be too simplistic. The natural extension is to use multiple parallel filters that represent these pathways. This more complex model structure, however, naturally brings about a more demanding task of extracting the model parameters from experimental data. Several earlier investigations have shown how generic multi-filter models can be obtained based on spike-triggered covariance analysis (de Ruyter van Steveninck and Bialek 1988; Schwartz et al. 2006) or on information theoretic approaches (Paninski 2003; Sharpee et al. 2004; Pillow and Simoncelli 2006).

In the examples presented here, the goal was to find filters that correspond to the synaptic inputs from a pool of bipolar cells, including both ON-type and OFF-type bipolar cells. One particular challenge for separating contributions from the ON and OFF pathways is that their preferred stimuli are nearly inverted with respect to each other. Therefore, they cannot naturally emerge as separate filters from a spike-triggered covariance analysis, for which the resulting filters are by design orthogonal to each other. Nevertheless, this covariance analysis serves as a good starting point because it singles out stimulus components for which the variance in the spike-triggered stimulus ensemble is particularly large. Such a stimulus component is a good candidate for providing a separation of clusters with nearly inverted stimulus characteristics.

One particular goal for focusing on separating ON- and OFF-pathway contributions is to use the resulting modeling framework as a data-analysis tool. The parameters of the model, such as the shapes of the filters and the relative strength of ON- and OFF-pathway contributions are here obtained for a specific stimulus context and will likely vary with this context. In the presented example, this context is given by the mean light intensity and the variance of the flickering light stimulus. Under different stimulus conditions, one may obtain different values for the model parameters, which could be used, for example, to investigate adaptation phenomena, similar to applications of the LN model (Chander and Chichilnisky 2001; Kim and Rieke 2001; Baccus and Meister 2002). In the discussed work of Geffen et al. [2007], the multi-filter model was used in this way to study the effect of saccadic stimulus shifts, which revealed that the weights of the ON- and OFF-pathways transiently change after the saccade. For a better mechanistic understanding of these adaptive and contextual effects on the gating of these pathways, future extensions of the multi-pathway model may aim at incorporating how these pathway weights are determined by the stimulus context.

The applied model structure can be viewed as a hybrid between a purely phenomenological and a biologically inspired approach; based on the descriptive LN model, the use of parallel, spatially localized ON and OFF filters aims at capturing properties of the neuronal circuit that are thought to be fundamental for the investigated phenomena. In the discussed examples, the involvement of ON and OFF pathways was corroborated by experiments under pharmacological perturbation of the circuitry.

Generally speaking, however, it should be noted that failure of the single-filter LN model does not always mean that a multi-filter model is required. In fact, additional dynamics that follow after stimulus integration, such as spike generation dynamics (Aguera y Arcas and Fairhall 2003; Fairhall et al. 2006) and spike time jitter (Aldworth et al. 2005; Dimitrov and Gedeon 2006; Gollisch 2006) can lead to the appearance of multiple relevant filters in a spike-triggered covariance analysis. Although the multi-filter models may then still provide accurate descriptions of the neuronal responses, extensions of the model cascade with explicit spike generation dynamics (Keat et al. 2001; Pillow et al. 2005) or additional filtering stages (Victor and Shapley 1979; Korenberg and Hunter 1986; Sakai 1992) may provide a closer match to the biological processes. In the retina, for example, other successful approaches include Wiener series modeling (Marmarelis and Naka 1972) and LNL cascades (Spekreijse 1969; Victor and Shapley 1979). In fact, by analyzing the structures of first- and second-order Wiener kernels, one may estimate whether within the realm of LNL cascades, linear filtering acts primarily before the nonlinear transformation, after it, or both (Victor and Shapley 1979, 1980; Korenberg and Hunter 1986; Korenberg et al. 1989).

For the ganglion-cell responses analyzed here, such an analysis supports the importance of linear filtering that precedes the nonlinearity. For some cells, the second-order Wiener kernel indicates additional filtering that follows after the nonlinearity, which may correspond to feedback dynamics resulting from adaptation or gain control. These dynamics are not included in the model structure discussed here, which instead focuses on capturing a specific aspect of the retinal circuitry, the convergence of ON and OFF pathways. For a more general model of the cells’ response characteristics, additional dynamics should also be considered.

Generalizing the model structure in such a way is straightforward; the parallel filters can act as a front end to existing modules for gain control (Victor 1987; Berry and Meister 1998; Berry et al. 1999; Pillow et al. 2005) or additional filtering (Spekreijse 1969; Victor and Shapley 1979), which would act on the activation function that results from combining the spatially localized ON and OFF filter contributions. Fitting the complete model structure to experimental data becomes, of course, increasingly challenging with increasing number of model parameters. How well it works will depend on the specific model extension and the amount of available data. A promising approach here seems to be to resort to maximum-likelihood estimation techniques, for which the parallel filters can be initialized by the shapes obtained from the separation procedure described here. This approach is also amenable to various desirable model extensions discussed below.

7.1 7.1 Shortcomings and extensions

One shortcoming of the current approach is the ad-hoc definition of the spatial subfields. For ease of analysis, the subfields are modeled as rectangular and non-overlapping, whereas actual bipolar cells are better described by a smooth center-surround structure (Dacey et al. 2000; Baccus et al. 2008) that suggests, for example, a “difference-of-Gaussians” model. To fit such a more elaborate model to data will require stimulation with finer spatial structures and consequently more experimental time for data acquisition.

A further weakness of the current approach is that it relies on a good separation of the two clusters corresponding to the ON and OFF pathways. Because each spike is fully assigned to one of the two clusters, any overlap of the clusters would distort the resulting filter shapes. This problem could become more severe for a system where the filters are not nearly inverted versions of each other; in that case, both pathways could be activated at the same time. A potential remedy would be to use the described procedure only to obtain an initial model estimate which is then refined, for example, by a maximum-likelihood fitting procedure (Paninski et al. 2004; Pillow et al. 2005). Initial explorations of this method showed that the obtained ON and OFF filters are robust in this respect—the maximum-likelihood procedure does not alter their shapes (Fig. 7b).

Fig. 7

ON and OFF filters and nonlinearities obtained from a maximum-likelihood analysis. Maximum-likelihood analysis was applied to the data of Fig. 5 obtained under spatially homogeneous flicker stimulation. The model consisted of two parallel temporal filters and subsequent nonlinearities, as in Fig. 2. The nonlinearities were here parameterized by a threshold and a second-order polynomial for values above the threshold. Using a Poisson process firing model, the model likelihood was iteratively maximized by a conjugate gradient ascent algorithm. a Spike-triggered averages of the separated clusters as in Fig. 5f. These were used as starting values of the algorithm. b Filters at the end of the algorithm. The final filters are nearly identical to the spike-triggered averages of a. c Nonlinearities associated with each filter. The final nonlinearities substantially differ from the original half-wave rectification, which is shown by the dashed line. In particular, the thresholds consistently assume values larger than zero

A simplification in the model comes from the fixed half-wave rectification that follows after each filter. The shape of this nonlinearity is motivated by findings that support rectification of synaptic inputs from bipolar cells to ganglion cells (Victor and Shapley 1979; Demb et al. 2001). For the case of spatially homogeneous stimulation, the shape of the nonlinear transformations could also be obtained from the experimental data by analyzing the relationship between the spikes from an individual spike-triggered stimulus cluster (Fig. 5d) and the output of the corresponding ON or OFF filter. For the case of flickering stripes, however, this approach is not suited because of the larger number of filters whose outputs simultaneously affect the firing rate. The relation between the firing rate and an individual filter (i.e., the marginal spike probability that depends only on a single filter output) is distorted by the large number of spikes that are generated primarily by activation from neighboring stripes. One may also consider a full multi-dimensional exploration of the nonlinearity by sampling the spike probability as depending on the joint outputs of all spatially local ON and OFF filters. However, given that around six to ten filters are typically required to span the receptive field center, this analysis is currently precluded by the large amounts of data that would be required for sufficient sampling. As a suitable alternative, a parameterization of the nonlinear transformation could be applied and included in a maximum-likelihood fitting procedure. Initial explorations suggest that threshold-linear or threshold-quadratic nonlinearities with positive thresholds may lead to an improved model version (Fig. 7c).

Finally, the spike-generation part of the model is currently limited to predicting the first spike in response to a stimulus. For a full account of the neuronal response, including the prediction of the time-dependent firing rate, more details are needed in the final model stage. In particular, effects of refractory period, adaptation, and contrast gain control need to be considered. Obtaining such a complete model description for spatiotemporal stimulation of ON-OFF-type neurons from experimental data will be a formidable, yet worthwhile task.