General three-dimensional scattering and dynamic stress concentration of Lamb-like waves in a spherical shell with a spherical inclusion

Abstract

Three-dimensional scattering and dynamic stress concentration of Lamb-like waves around a spherical inclusion (inhomogeneity and a cavity) in a thick spherical shell are investigated theoretically and numerically. Two spherical coordinates, located at the spherical shell center and the inclusion center, are established to express the incident and scattered wave potential functions. By a kind of addition formulas, all the potential functions can be transformed into the same coordinate, then the analytical solution of the displacements and stresses are derived, and all the undetermined coefficients are solved by satisfying the boundary condition and the interface condition. In order to describe the 3-D stresses concentration, multiple DSCFs are employed and the 3-D distributions are depicted. The results reveal the influences of inclusion material and the cavity on the distributions of DSCFs, and the influence of incident wave frequency and inclusion position are also calculated. This research is expected to provide theoretical understanding on dynamic analysis and mechanical properties evaluation of the spherical shells.

Appendices

Appendix 1: The relation between the incident wave amplitudes $A_{11}^\mathrm{I}$ and $C_{11}^\mathrm{I}$

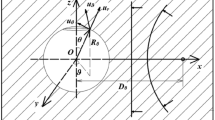
As it is described in Fig. 22, the incident waves are coupled by the P- and SV-wave of the same incident angle $\left( {\theta _0 ,\varphi _0 } \right)$.

In the Cartesian coordinate system $\left( {x_1 ,y_1 ,z_1 } \right)$ the potential functions for the incident wave can be presented as:

$$\begin{aligned} \eta _{11}^\mathrm{I}= & {} A_{11}^\mathrm{I} \exp \left[ {\hbox {i}\alpha _1 \left( {x_1 \sin \theta _0 \cos \varphi _0 +y_1 \sin \theta _0 \sin \varphi _0 +z_1 \cos \theta _0 } \right) -\omega t} \right] \end{aligned}$$

(59)

$$\begin{aligned} \chi _{11}^\mathrm{I}= & {} C_{11}^\mathrm{I} \exp \left[ {\hbox {i}\beta _1 \left( {x_1 \sin \theta _0 \cos \varphi _0 +y_1 \sin \theta _0 \sin \varphi _0 +z_1 \cos \theta _0 } \right) -\omega t} \right] \end{aligned}$$

(60)

where $A_{11}^\mathrm{I}$, $C_{11}^\mathrm{I}$ refer to the amplitudes of P-wave and SV-wave, and $\alpha _1$, $\beta _1$ denote the wave number for P-wave and SV-wave, respectively.

Fig. 22

The location of the incident wave plane

As it is well known that P- and SV-wave propagate in the same wave plane, which means that the projection of displacements on the normal of the wave plane is equal to 0. For convenience, the plane which is perpendicular to $x_1 o_1 y_1$ is assumed as the wave plane, and the normal of the wave plane is given as

$$\begin{aligned} \mathbf{N}=\sin \varphi _N \mathbf{e}_x -\cos \varphi _N \mathbf{e}_y \end{aligned}$$

(61)

with $\varphi _N =\varphi _0 -\pi /2$.

In this case, $\mathbf{u}$ can be rewritten as

$$\begin{aligned} \mathbf{u}=\exp \left( {\hbox {i}\omega t} \right) \left( {\nabla \eta +\nabla \times \left( {\psi \mathbf{e}_z } \right) +\nabla \times \nabla \times \left( {\chi \mathbf{e}_z } \right) } \right) \end{aligned}$$

(62)

where $\nabla$ means the Laplace operator in the Cartesian coordinate system. Thus, from the equation that

$$\begin{aligned} \mathbf{u}\cdot \mathbf{N}=0 \end{aligned}$$

(63)

the relation between the amplitudes $A_{11}^\mathrm{I}$ and $C_{11}^\mathrm{I}$ is obtained

$$\begin{aligned} \frac{A_{11}^\mathrm{I} }{C_{11}^\mathrm{I} }=\frac{\beta _1^2 \cos \theta _0 }{\alpha _1 } \end{aligned}$$

(64)

It is obviously that the relation is independent of the assumption of the wave plane.

Appendix 2: The addition formula for $h_l^{\left( 2 \right) } \bar{{Y}}_{{l}'{m}'}$

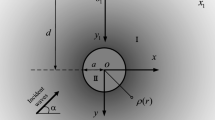
In this appendix expansion form of the addition formula into the series in terms of $h_l^{\left( 2 \right) } \bar{{Y}}_{{l}'{m}'}$ is derived. As shown in Fig. 23, $O_1$ and $O_2$ are the two origins of the different spherical coordinates,

Fig. 23

The relation among $\mathbf{r}_1$, $\mathbf{r}_2$ and $\mathbf{R}_{12}$

The bicentric expansion form of Green function is expressed as [24] :

$$\begin{aligned} G\left( {\mathbf{r}_0 ,\mathbf{r}_2 ,\mathbf{R}_{12} ;K} \right)= & {} 8\mathop {\sum }\limits _L {\mathop {\sum }\limits _{{L}'} {\mathop {\sum }\limits _{{L}''} {\left( {-1} \right) ^{l+1}i^{l+{l}'+{l}''}Q_{{L}''} \left( {L{L}'} \right) } } }\nonumber \\&\times F_{l{l}'{l}''} \left( {\mathbf{r}_0 ,\mathbf{r}_2 ,\mathbf{R}_{12} ;K} \right) Y_{lm} \left( {\theta _0 ,\varphi _0 } \right) \bar{{Y}}_{{l}'{m}'} \left( {\theta _2 ,\varphi _2 } \right) \bar{{Y}}_{{l}''{m}''} \left( {\theta _{12} ,\varphi _{12} } \right) \end{aligned}$$

(65)

where

$$\begin{aligned} Q_{{l}''} \left( {l{l}'} \right) =\left( {-1} \right) ^{m}\left[ {\frac{\left( {2l+1} \right) \left( {2{l}'+1} \right) \left( {2{l}''+1} \right) }{4\pi }} \right] ^{1/2}\left( {{\begin{array}{l@{\quad }l@{\quad }l} l&{} {{l}'}&{} {{l}''} \\ 0&{} 0&{} 0 \\ \end{array} }} \right) \left( {{\begin{array}{l@{\quad }l@{\quad }l} l&{} {{l}'}&{} {{l}''} \\ {-m}&{} {{m}'}&{} {-{m}''} \\ \end{array} }} \right) \end{aligned}$$

(66)

And the radial coefficient is given by

$$\begin{aligned} F_{l{l}'{l}''} \left( {\mathbf{r}_0 ,\mathbf{r}_2 ,\mathbf{R}_{12} ;K} \right) =\int _0^\infty {\frac{q^{2}j_l \left( {qr_0 } \right) j_{{l}'} \left( {qr_2 } \right) j_{{l}''} \left( {qR_{12} } \right) }{q^{2}-K^{2}}} dq \end{aligned}$$

(67)

and as it is known Eq. (67) in the region $I(r_0 +r_2 \le R_{12} )$ is obtained as following [24]:

$$\begin{aligned} F_{l{l}'{l}''}^{\left( I \right) } \left( {\mathbf{r}_0 ,\mathbf{r}_2 ,\mathbf{R}_{12} ;K} \right) =\frac{\pi \hbox {i}}{2}Kj_l \left( {Kr_0 } \right) j_{{l}'} \left( {Kr_2 } \right) h_{_{{l}''} }^{\left( 1 \right) } \left( {KR_{12} } \right) \end{aligned}$$

(68)

And the bicentric expansion form Eq. (65) is rewritten as

$$\begin{aligned} G\left( {\mathbf{r}_0 ,\mathbf{r}_2 ,\mathbf{R}_{12} ;K} \right) =\hbox {i}K\mathop {\sum }\limits _L {\mathop {\sum }\limits _{{L}'} {F_{L{L}'}^{\left( 1 \right) } \left( {K\mathbf{R}_{12} } \right) j_l \left( {Kr_0 } \right) j_{{l}'} \left( {Kr_2 } \right) Y_{lm} \left( {\theta _0 ,\varphi _0 } \right) \bar{{Y}}_{{l}'{m}'} \left( {\theta _2 ,\varphi _2 } \right) } } \end{aligned}$$

(69)

with

$$\begin{aligned} F_{L{L}'}^{\left( 1 \right) } \left( {K\mathbf{R}_{12} } \right) =\mathop {\sum }\limits _{{L}''} {4\pi \left( {-1} \right) ^{l}\hbox {i}^{l+{l}'+{l}''}Q_{{L}''} \left( {L{L}'} \right) h_{{l}''}^{\left( 1 \right) } \left( {KR_{12} } \right) \bar{{Y}}_{{l}''{m}''} \left( {\theta _{12} ,\varphi _{12} } \right) } \end{aligned}$$

(70)

Similarly, in the region II ($r_2 +R_{12} <r_0$), the integral in Eq. (67) can be calculated by contour integral as

$$\begin{aligned} F_{l{l}'{l}''}^{\left( {II} \right) } \left( {\mathbf{r}_0 ,\mathbf{r}_2 ,\mathbf{R}_{12} ;K} \right) =\frac{\pi \hbox {i}}{2}Kh_l^{\left( 2 \right) } \left( {Kr_0 } \right) j_{{l}'} \left( {Kr_0 } \right) j_{{l}''} \left( {KR_{12} } \right) \end{aligned}$$

(71)

Furthermore, let $\lim R_{12} \rightarrow 0$, the classical expansion of Green function can be obtained from Eq. (71)

$$\begin{aligned} G\left( {\mathbf{r}_1 ,\mathbf{r}_0 } \right) =\hbox {i}K\mathop {\sum }\limits _L {h_l^{\left( 2 \right) } \left( {Kr_1 } \right) j_l \left( {Kr_0 } \right) Y_{lm} \left( {\theta _0 ,\varphi _0 } \right) Y_{lm}^{*} \left( {\theta _1 ,\varphi _1 } \right) } \quad \left( {r_0 >r_1 } \right) \end{aligned}$$

(72)

According to the orthotropic character of $Y_{lm}$, the following addition formula can be deduced

$$\begin{aligned} h_l^{\left( 2 \right) } \left( {Kr_1 } \right) \bar{{Y}}_{lm} \left( {\theta _1 ,\varphi _1 } \right)= & {} \mathop {\sum }\limits _{{L}'} \mathop {\sum }\limits _{{L}''} 4\pi \left( {-1} \right) ^{l}\hbox {i}^{l+{l}'+{l}''}Q_{{L}'} \left( {L,{L}'} \right) h_{{l}''}^{\left( 1 \right) } \left( {KR_{12} } \right) \bar{{Y}}_{{l}''{m}''} \left( {\theta _{12} ,\varphi _{12} } \right) j_{{l}'} \left( {Kr_2 } \right) \bar{{Y}}_{{l}'{m}'} \nonumber \\&\quad \left( {\theta _2 ,\varphi _2 } \right) \quad (r_2 \le R_{12} ) \end{aligned}$$

(73)

Appendix 3: The elements in Eqs. (29)–(31), and (37)–(44)

The expression of $T_{ij,l}^\gamma$ and $T_{5w,l}^\gamma$ in Eqs. (29)–(31) is listed as follows:

$$\begin{aligned} T_{11,l}^\gamma \left( {r_1 } \right)= & {} 2\mu _1 \left( {\frac{l^{2}-l}{r_1^2 }b_l \left( {\alpha _1 r_1 } \right) -\frac{1}{2}\beta _1^2 b_l \left( {\alpha _1 r_1 } \right) +\frac{2\alpha _1 }{r_1 }b_{l+1} \left( {\alpha _1 r_1 } \right) } \right) ;\\ T_{12,l}^\gamma \left( {r_1 } \right)= & {} 2\mu _1 \;l\left( {l+1} \right) \left( {\frac{l-1}{r_1^2 }b_l \left( {\beta _1 r_1 } \right) -\frac{\beta _1 }{r_1^2 }b_{l+1} \left( {\beta _1 r_1 } \right) } \right) ;\\ T_{21,l}^\gamma \left( {r_1 } \right)= & {} 2\mu _1 \left( {\frac{l-1}{r_1^2 }b_l \left( {\alpha _1 r_1 } \right) -\frac{\alpha _1 }{r_1 }b_{l+1} \left( {\alpha _1 r_1 } \right) } \right) ;\\ T_{22,l}^\gamma \left( {r_1 } \right)= & {} \mu _1 \left( {\frac{2\beta _1 }{r_1 }b_{l+1} \left( {\beta _1 r_1 } \right) +\frac{2\left( {l^{2}-1} \right) }{r_1^2 }b_l \left( {\beta _1 r_1 } \right) -\beta _1^2 b_l \left( {\beta _1 r_1 } \right) } \right) \\ T_{5w,l}^\gamma \left( {r_1 } \right)= & {} \frac{l-1}{r_1 }b_l \left( {\alpha _1 r_1 } \right) -\alpha _1 b_{l+1} \left( {\alpha _1 r_1 } \right) . \end{aligned}$$

$T_{ij,l}^\gamma (i=1,2;j=1,2)$ and $T_{5w,l}^\gamma (w=7,8,9)$ stand for the radial coefficients of stresses, in which the superscript $\gamma =\hbox {S}1$, $\hbox {S2}$, $\hbox {S3}$ and $\hbox {I}$ correspond to the cases of the scattered waves evoked from the inclusion, the inner boundary, the outer boundary in the shell and the case of the incident waves, respectively. Also, for the case $\gamma =\hbox {S}1$, $\hbox {S2}$, $\hbox {S3}$ and $\hbox {I}$, $b_l$ is accordingly taken as $h_l^{\left( 1 \right) }$, $h_l^{\left( 1 \right) }$, $h_l^{\left( 2 \right) }$ and $j_l$.

The expression of $\Gamma _{ij,{l}'}^\gamma$, $\Gamma _{3w,{l}'}^\gamma$, $U_{ij,{l}'}^\gamma$ and $U_{3w,{l}'}^\gamma$ in Eqs. (37)–(44) is listed as follows

$$\begin{aligned} \Gamma _{11,{l}'}^\gamma \left( {r_2 } \right)= & {} -\lambda _k \alpha _k^2 b_{{l}'} \left( {\alpha _k r_2 } \right) +2\mu _k \left( {\frac{2\alpha _k }{r_2 }b_{{l}'+1} \left( {\alpha _k r_2 } \right) +\frac{{l}'^{2}-{l}'}{r_2^2 }b_{{l}'} \left( {\alpha _k r_2 } \right) -\alpha _k^2 b_{{l}'} \left( {\alpha _k r_2 } \right) } \right) ;\\ \Gamma _{12,{l}'}^\gamma \left( {r_2 } \right)= & {} 2\mu _k \;{l}'\left( {{l}'+1} \right) \left( {\frac{{l}'-1}{r_2^2 }b_{{l}'} \left( {\beta _k r_2 } \right) -\frac{\beta _k }{r_2^2 }b_{{l}'+1} \left( {\beta _k r_2 } \right) } \right) ;\\ \Gamma _{21,{l}'}^\gamma= & {} 2\mu _k \left( {\frac{{l}'-1}{r_2^2 }b_{{l}'} \left( {\alpha _k r_2 } \right) -\frac{\alpha _k }{r_2 }b_{{l}'+1} \left( {\alpha _k r_2 } \right) } \right) ;\\ \Gamma _{22,{l}'}^\gamma= & {} \mu _k \left( {\frac{2\beta _k }{r_2 }b_{{l}'+1} \left( {\beta _k r_2 } \right) +\frac{2\left( {{l}'^{2}-1} \right) }{r_2^2 }b_{{l}'} \left( {\beta _k r_2 } \right) -\beta _k^2 b_{{l}'} \left( {\beta _k r_2 } \right) } \right) ;\\ T_{3w,{l}'}^\gamma \left( {r_2 } \right)= & {} \frac{{l}'-1}{r_2 }b_{{l}'} \left( {\alpha _k r_2 } \right) -\alpha _k b_{{l}'+1} \left( {\alpha _k r_2 } \right) ;\\ U_{11,{l}'}^\gamma \left( {r_2 } \right)= & {} \frac{{l}'}{r_2 }b_{{l}'} \left( {\alpha _k r_2 } \right) -\alpha _1 b_{{l}'+1} \left( {\alpha _k r_2 } \right) ; \quad U_{12,{l}'}^\gamma ={l}'\left( {{l}'+1} \right) \frac{b_{{l}'} \left( {\beta _k r_2 } \right) }{r_2 };\\ U_{21,{l}'}^\gamma= & {} \frac{b_{{l}'} \left( {\alpha _k r_2 } \right) }{r_2 }; \quad U_{22,{l}'}^\gamma =\frac{{l}'+1}{r_2 }b_{{l}'} \left( {\beta _k r_2 } \right) -\beta _k b_{{l}'+1} \left( {\beta _k r_2 } \right) ; \quad U_{3w,{l}'}^\gamma =b_{{l}'} \left( {\alpha _k r_2 } \right) . \end{aligned}$$

$\Gamma _{ij,{l}'}^\gamma (i=1,2;j=1,2)$ and $\Gamma _{3w,{l}'}^\gamma (w=1,7,8,9)$ stands for the radial coefficients of stresses, $U_{ij,{l}'}^\gamma$ and $U_{3w,{l}'}^\gamma$ stand for the radial coefficients of displacements, in which the superscript $\gamma =\hbox {S}1$, $\hbox {S2}$, $\hbox {S3}$, $\hbox {I}$ and $\hbox {F}$ correspond to the cases of the scattered waves evoked from the inclusion, the inner boundary, the outer boundary in the shell, the case of the incident waves and the case of the standing waves in the inclusion, respectively. Also, for the case $\gamma =\hbox {S}1$, $\hbox {S2}$, $\hbox {S3}$, $\hbox {I}$ and $\hbox {F}$, $b_l$ is accordingly taken as $h_l^{\left( 1 \right) }$, $h_l^{\left( 1 \right) }$, $h_l^{\left( 2 \right) }$ and $j_l$. Meanwhile, $k=1$ when $\gamma =\hbox {S}1$, $\hbox {S2}$, $\hbox {S3}$ and $\hbox {I}$; $k=2$ when $\gamma =\hbox {F}$

Appendix 4: The solution processes for the unknown coefficients

From the boundary conditions (48) and interface conditions (50), the amplitudes $A_{L_2 }^{\mathrm{S}1}$, $C_{L_2 }^{\mathrm{S}1}$, $A_{L_1 }^{\mathrm{S2}}$, $C_{L_1 }^{\mathrm{S2}}$, $A_{L_1 }^{\mathrm{S3}}$, $C_{L_1 }^{\mathrm{S3}}$, $D_{L_1 }^\mathrm{F}$ and $F_{L_1 }^\mathrm{F}$ could be solved by the following process.

From the boundary conditions (48) we can obtain

$$\begin{aligned} \begin{array}{l} \left\{ {{\begin{array}{l} {A_{L_1 }^{\mathrm{S2}} } \\ {C_{L_1 }^{\mathrm{S2}} } \\ {A_{L_1 }^{\mathrm{S3}} } \\ {C_{L}^{\mathrm{S3}} } \\ \end{array} }} \right\} =-\left[ {{\begin{array}{l@{\quad }l} {{\begin{array}{l@{\quad }l} {T_{11,\;L_1 }^{\mathrm{S2}} \left( R \right) }&{} {T_{12,\;L_1 }^{\mathrm{S2}} \left( R \right) } \\ {T_{21,\;L_1 }^{\mathrm{S2}} \left( R \right) }&{} {T_{22,\;L_1 }^{\mathrm{S2}} \left( R \right) } \\ {T_{12,\;L_1 }^{\mathrm{S2}} \left( r \right) }&{} {T_{12,\;L_1 }^{\mathrm{S2}} \left( r \right) } \\ {T_{21,\;L_1 }^{\mathrm{S2}} \left( r \right) }&{} {T_{22,\;L_1 }^{\mathrm{S2}} \left( r \right) } \\ \end{array} }}&{} {{\begin{array}{l@{\quad }l} {T_{11,\;L_1 }^{\mathrm{S3}} \left( R \right) }&{} {T_{12,\;L_1 }^{\mathrm{S3}} \left( R \right) } \\ {T_{21,\;L_1 }^{\mathrm{S3}} \left( R \right) }&{} {T_{22,\;L_1 }^{\mathrm{S3}} \left( R \right) } \\ {T_{11,\;L_1 }^{\mathrm{S3}} \left( r \right) }&{} {T_{12,\;L_1 }^{\mathrm{S3}} \left( r \right) } \\ {T_{21,\;L_1 }^{\mathrm{S3}} \left( r \right) }&{} {T_{22,\;L_1 }^{\mathrm{S3}} \left( r \right) } \\ \end{array} }} \\ \end{array} }} \right] ^{-1} \\ \left( {\left[ {{\begin{array}{l@{\quad }l} {T_{11,\;L_1 }^{\mathrm{S}1} \left( R \right) }&{} {T_{12,\;L_1 }^{\mathrm{S}1} \left( R \right) } \\ {T_{21,\;L_1 }^{\mathrm{S}1} \left( R \right) }&{} {T_{22,\;L_1 }^{\mathrm{S}1} \left( R \right) } \\ {T_{11,\;L_1 }^{\mathrm{S}1} \left( r \right) }&{} {T_{12,\;L_1 }^{\mathrm{S}1} \left( r \right) } \\ {T_{21,\;L_1 }^{\mathrm{S}1} \left( r \right) }&{} {T_{22,\;L_1 }^{\mathrm{S}1} \left( r \right) } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {A_{L_1 }^{\mathrm{S}1} } \\ {C_{L_1 }^{\mathrm{S}1} } \\ \end{array} }} \right\} +\left[ {{\begin{array}{l@{\quad }l} {T_{11,\;L_1 }^\mathrm{I} \left( R \right) }&{} {T_{12,\;L_1 }^\mathrm{I} \left( R \right) } \\ {T_{21,\;L_1 }^\mathrm{I} \left( R \right) }&{} {T_{22,\;L_1 }^\mathrm{I} \left( R \right) } \\ {T_{11,\;L_1 }^\mathrm{I} \left( r \right) }&{} {T_{12,\;L_1 }^\mathrm{I} \left( r \right) } \\ {T_{21,\;L_1 }^\mathrm{I} \left( r \right) }&{} {T_{22,\;L_1 }^\mathrm{I} \left( r \right) } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {A^\mathrm{I} } \\ {C^\mathrm{I} } \\ \end{array} }} \right\} } \right) \\ \end{array} \end{aligned}$$

(74)

and the amplitudes $A_{L_1 }^{\mathrm{S2}}$, $C_{L_1 }^{\mathrm{S2}}$, $A_{L_1 }^{\mathrm{S3}}$ and $C_{L_1 }^{\mathrm{S3}}$ can be expressed in the form

$$\begin{aligned} \left\{ {{\begin{array}{l} {A_{L_2 }^{\mathrm{S2}} } \\ {C_{L_2 }^{\mathrm{S}2} } \\ {A_{L_2 }^{\mathrm{S3}} } \\ {C_{L_2 }^{\mathrm{S3}} } \\ \end{array} }} \right\} =\mathop {\sum }\limits _{L_1 } {\mathbf{F}_1 \left\{ {{\begin{array}{l} {A_{L_1 }^{\mathrm{S2}} } \\ {C_{L_1 }^{\mathrm{S}2} } \\ {A_{L_1 }^{\mathrm{S3}} } \\ {C_{L_1 }^{\mathrm{S3}} } \\ \end{array} }} \right\} } \end{aligned}$$

(75)

where the matrix

$$\begin{aligned} \mathbf{F}_1 =\left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {F_1 \left( {L_1 ,L_2 ,\alpha _1 } \right) }&{} &{} &{} \\ &{} {F_1 \left( {L_1 ,L_2 ,\beta _1 } \right) }&{} &{} \\ &{} &{} {F_1 \left( {L_1 ,L_2 ,\alpha _1 } \right) }&{} \\ &{} &{} &{} {F_1 \left( {L_1 ,L_2 ,\beta _1 } \right) } \\ \end{array} }} \right] \end{aligned}$$

(76)

Substitution of Eqs. (75) and (74) into Eq. (50) leads to

$$\begin{aligned} \begin{array}{l} \left( {\mathop {\sum }\limits _{L_{_1 } } {\left[ {{\begin{array}{l@{\quad }l} {T_{11,\;L_2 }^\mathrm{I} \left( {r_0 } \right) } &{} {T_{12,\;L_2 }^\mathrm{I} \left( {r_0 } \right) } \\ {T_{21,\;L_2 }^\mathrm{I} \left( {r_0 } \right) } &{} {T_{22,\;L_2 }^\mathrm{I} \left( {r_0 } \right) } \\ {U_{11,\;L_2 }^\mathrm{I} \left( {r_0 } \right) } &{} {U_{12,\;L_2 }^\mathrm{I} \left( {r_0 } \right) } \\ {U_{21,\;L_2 }^\mathrm{I} \left( {r_0 } \right) } &{} {U_{22,\;L_2 }^\mathrm{I} \left( {r_0 } \right) } \\ \end{array} }} \right] \mathbf{F}_2 } -\mathop {\sum }\limits _{L_1 } {\mathbf{M}_{L_1 } } \left[ {{\begin{array}{l@{\quad }l} {T_{11,\;L_1 }^\mathrm{I} \left( R \right) }&{} {T_{12,\;L_1 }^\mathrm{I} \left( R \right) } \\ {T_{12,\;L_1 }^\mathrm{I} \left( R \right) }&{} {T_{22,\;L_1 }^\mathrm{I} \left( R \right) } \\ {T_{11,\;L_1 }^\mathrm{I} \left( r \right) }&{} {T_{12,\;L_1 }^\mathrm{I} \left( r \right) } \\ {T_{12,\;L_1 }^\mathrm{I} \left( r \right) }&{} {T_{22,\;L_1 }^\mathrm{I} \left( r \right) } \\ \end{array} }} \right] } \right) \left\{ {{\begin{array}{l} {A^\mathrm{I} } \\ {C^\mathrm{I} } \\ \end{array} }} \right\} \\ +\left( {\left[ {{\begin{array}{l@{\quad }l} {T_{11,\;L_1 }^{\mathrm{S1}} \left( {r_0 } \right) } &{} {T_{12,\;L_1 }^{\mathrm{S1}} \left( {r_0 } \right) } \\ {T_{21,\;L_1 }^{\mathrm{S1}} \left( {r_0 } \right) } &{} {T_{22,\;L_1 }^{\mathrm{S1}} \left( {r_0 } \right) } \\ {U_{11,\;L_1 }^{\mathrm{S1}} \left( {r_0 } \right) } &{} {U_{12,\;L_1 }^{\mathrm{S1}} \left( {r_0 } \right) } \\ {U_{21,\;L_1 }^{\mathrm{S1}} \left( {r_0 } \right) } &{} {U_{22,\;L_1 }^{\mathrm{S1}} \left( {r_0 } \right) } \\ \end{array} }} \right] -\mathop {\sum }\limits _{L_2 } {\mathop {\sum }\limits _{L_1 } {\mathbf{M}_{L} } } \left[ {{\begin{array}{l@{\quad }l} {T_{11,\;L_1 }^{\mathrm{S}1} \left( R \right) }&{} {T_{12,\;L_1 }^{\mathrm{S}1} \left( R \right) } \\ {T_{12,\;L_1 }^{\mathrm{S}1} \left( R \right) }&{} {T_{22,\;L_1 }^{\mathrm{S}1} \left( R \right) } \\ {T_{11,\;L_1 }^{\mathrm{S}1} \left( r \right) }&{} {T_{12,\;L_1 }^{\mathrm{S}1} \left( r \right) } \\ {T_{12,\;L_1 }^{\mathrm{S}1} \left( r \right) }&{} {T_{22,\;L_1 }^{\mathrm{S}1} \left( r \right) } \\ \end{array} }} \right] \mathbf{F}_1 } \right) \left\{ {{\begin{array}{l} {A_{L_2 }^{\mathrm{S}1} } \\ {C_{L_2 }^{\mathrm{S}1} } \\ \end{array} }} \right\} \\ =\left[ {{\begin{array}{l@{\quad }l} {T_{11,\;L_1 }^\mathrm{F} \left( {r_0 } \right) } &{} {T_{12,\;L_1 }^\mathrm{F} \left( {r_0 } \right) } \\ {T_{21,\;L_1 }^\mathrm{F} \left( {r_0 } \right) } &{} {T_{22,\;L_1 }^\mathrm{F} \left( {r_0 } \right) } \\ {U_{11,\;L_1 }^\mathrm{F} \left( {r_0 } \right) } &{} {U_{12,\;L_1 }^\mathrm{F} \left( {r_0 } \right) } \\ {U_{21,\;L_1 }^\mathrm{F} \left( {r_0 } \right) } &{} {U_{22,\;L_1 }^\mathrm{F} \left( {r_0 } \right) } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {D_{L_2 }^\mathrm{F} } \\ {F_{L_2 }^\mathrm{F} } \\ \end{array} }} \right\} \\ \end{array} \end{aligned}$$

(77)

where the matrix

$$\begin{aligned} \mathbf{M}_{L_1 }= & {} \left[ {{\begin{array}{l@{\quad }l} {{\begin{array}{l@{\quad }l} {T_{11,\;L_2 }^{\mathrm{S2}} \left( {r_0 } \right) } &{} {T_{12,\;L_2 }^{\mathrm{S2}} \left( {r_0 } \right) } \\ {T_{21,\;L_2 }^{\mathrm{S2}} \left( {r_0 } \right) } &{} {T_{22,\;L_2 }^{\mathrm{S2}} \left( {r_0 } \right) } \\ {U_{11,\;L_2 }^{\mathrm{S2}} \left( {r_0 } \right) } &{} {U_{12,\;L_2 }^{\mathrm{S2}} \left( {r_0 } \right) } \\ {U_{21,\;L_2 }^{\mathrm{S2}} \left( {r_0 } \right) } &{} {U_{22,\;L_2 }^{\mathrm{S2}} \left( {r_0 } \right) } \\ \end{array} }}&{} {{\begin{array}{l@{\quad }l} {T_{11,\;L_2 }^{\mathrm{S3}} \left( {r_0 } \right) } &{} {T_{12,\;L_2 }^{\mathrm{S3}} \left( {r_0 } \right) } \\ {T_{21,\;L_2 }^{\mathrm{S3}} \left( {r_0 } \right) } &{} {T_{22,\;L_2 }^{\mathrm{S3}} \left( {r_0 } \right) } \\ {U_{11,\;L_2 }^{\mathrm{S3}} \left( {r_0 } \right) } &{} {U_{12,\;L_2 }^{\mathrm{S3}} \left( {r_0 } \right) } \\ {U_{21,\;L_2 }^{\mathrm{S3}} \left( {r_0 } \right) } &{} {U_{22,\;L_2 }^{\mathrm{S3}} \left( {r_0 } \right) } \\ \end{array} }} \\ \end{array} }} \right] \nonumber \\&\quad \mathbf{F}_1 \left[ {{\begin{array}{l@{\quad }l} {{\begin{array}{l@{\quad }l} {T_{11,\;L_2 }^{\mathrm{S2}} \left( R \right) }&{} {T_{12,\;L_2 }^{\mathrm{S2}} \left( R \right) } \\ {T_{21,\;L_2 }^{\mathrm{S2}} \left( R \right) }&{} {T_{22,\;L_2 }^{\mathrm{S2}} \left( R \right) } \\ {T_{11,\;L_2 }^{\mathrm{S2}} \left( r \right) }&{} {T_{12,\;L_2 }^{\mathrm{S2}} \left( r \right) } \\ {T_{21,\;L_2 }^{\mathrm{S2}} \left( r \right) }&{} {T_{22,\;L_2 }^{\mathrm{S2}} \left( r \right) } \\ \end{array} }}&{} {{\begin{array}{l@{\quad }l} {T_{11,\;L_2 }^{\mathrm{S3}} \left( R \right) }&{} {T_{12,\;L_2 }^{\mathrm{S3}} \left( R \right) } \\ {T_{21,\;L_2 }^{\mathrm{S3}} \left( R \right) }&{} {T_{22,\;L_2 }^{\mathrm{S3}} \left( R \right) } \\ {T_{11,\;L_2 }^{\mathrm{S3}} \left( r \right) }&{} {T_{12,\;L_2 }^{\mathrm{S3}} \left( r \right) } \\ {T_{21,\;L_2 }^{\mathrm{S3}} \left( r \right) }&{} {T_{22,\;L_2 }^{\mathrm{S3}} \left( r \right) } \\ \end{array} }} \\ \end{array} }} \right] ^{-1} \end{aligned}$$

(78)

and the matrices

$$\begin{aligned} \mathbf{F}_2 =\hbox {i}^{l_1 }\bar{{Y}}_{l_1 m_1 } \left( {\theta _0 ,\varphi _0 } \right) \left[ {{\begin{array}{l@{\quad }l} {F_2 \left( {L_1 ,L_2 ,\alpha _1 } \right) }&{} \\ &{} {F_2 \left( {L_1 ,L_2 ,\beta _1 } \right) } \\ \end{array} }} \right] \end{aligned}$$

(79)

Let

$$\begin{aligned} \left[ {{\begin{array}{l@{\quad }l} {\tilde{T}_{11}^\mathrm{S} \left( R \right) }&{} {\tilde{T}_{12}^\mathrm{S} \left( R \right) } \\ {\tilde{T}_{21}^\mathrm{S} \left( R \right) }&{} {\tilde{T}_{22}^\mathrm{S} \left( R \right) } \\ {\tilde{T}_{31}^\mathrm{S} \left( r \right) }&{} {\tilde{T}_{32}^\mathrm{S} \left( r \right) } \\ {\tilde{T}_{41}^\mathrm{S} \left( r \right) }&{} {\tilde{T}_{42}^\mathrm{S} \left( r \right) } \\ \end{array} }} \right] =\mathop {\sum }\limits _{L_1 } {\mathbf{M}_{L_1 } \left[ {{\begin{array}{l@{\quad }l} {{\begin{array}{l@{\quad }l} {T_{11,\;L_1 }^{\mathrm{S}1} \left( R \right) }&{} {T_{12,\;L_1 }^{\mathrm{S}1} \left( R \right) } \\ {T_{12,\;L_1 }^{\mathrm{S}1} \left( R \right) }&{} {T_{22,\;L_1 }^{\mathrm{S}1} \left( R \right) } \\ {T_{11,\;L_1 }^{\mathrm{S}1} \left( r \right) }&{} {T_{12,\;L_1 }^{\mathrm{S}1} \left( r \right) } \\ {T_{12,\;L_1 }^{\mathrm{S}1} \left( r \right) }&{} {T_{22,\;L_1 }^{\mathrm{S}1} \left( r \right) } \\ \end{array} }}&{} {{\begin{array}{l@{\quad }l} 0&{} 0 \\ 0&{} 0 \\ 0&{} 0 \\ 0&{} 0 \\ \end{array} }} \\ \end{array} }} \right] \mathbf{F}_1 } \end{aligned}$$

(80)

Then for each expansion term k, n Eq. (77) can be rewritten as

$$\begin{aligned} \begin{array}{l} \mathop {\sum }\limits _{L_2 } {\left[ {{\begin{array}{l@{\quad }l} {{\begin{array}{l@{\quad }l} {\delta _{l_2 k} \delta _{m_2 n} T_{11,\;L_2 }^{\mathrm{S1}} \left( {r_0 } \right) -\tilde{T}_{11,\;L_2 }^\mathrm{S} \left( R \right) }&{} {\delta _{l_2 k} \delta _{m_2 n} T_{12,\;L_2 }^{\mathrm{S1}} \left( {r_0 } \right) -\tilde{T}_{12,\;L_2 }^\mathrm{S} \left( R \right) } \\ {\delta _{l_2 k} \delta _{m_2 n} T_{21,\;L_2 }^{\mathrm{S1}} \left( {r_0 } \right) -\tilde{T}_{12,\;L_2 }^\mathrm{S} \left( R \right) }&{} {\delta _{l_2 k} \delta _{m_2 n} T_{22,\;L_2 }^{\mathrm{S1}} \left( {r_0 } \right) -\tilde{T}_{22,\;L_2 }^\mathrm{S} \left( R \right) } \\ {\delta _{l_2 k} \delta _{m_2 n} U_{11,\;L_2 }^{\mathrm{S1}} \left( {r_0 } \right) -\tilde{T}_{13,\;L_2 }^\mathrm{S} \left( r \right) }&{} {\delta _{l_2 k} \delta _{m_2 n} U_{12,\;L_2 }^{\mathrm{S1}} \left( {r_0 } \right) -\tilde{T}_{23,\;L_2 }^\mathrm{S} \left( r \right) } \\ {\delta _{l_2 k} \delta _{m_2 n} U_{21,\;L_2 }^{\mathrm{S1}} \left( {r_0 } \right) -\tilde{T}_{14,\;L_2 }^\mathrm{S} \left( r \right) }&{} {\delta _{l_2 k} \delta _{m_2 n} U_{22,\;L_2 }^{\mathrm{S1}} \left( {r_0 } \right) -\tilde{T}_{24,\;L_2 }^\mathrm{S} \left( r \right) } \\ \end{array} }}&{} {{\begin{array}{l@{\quad }l} {-\delta _{l_2 k} \delta _{m_2 n} \Gamma _{11,\;L_2 }^\mathrm{F} \left( {r_0 } \right) } &{} {-\delta _{l_2 k} \delta _{m_2 n} T_{12,\;L_2 }^\mathrm{F} \left( {r_0 } \right) } \\ {-\delta _{l_2 k} \delta _{m_2 n} \Gamma _{21,\;L_2 }^\mathrm{F} \left( {r_0 } \right) } &{} {-\delta _{l_2 k} \delta _{m_2 n} T_{22,\;L_2 }^\mathrm{F} \left( {r_0 } \right) } \\ {-\delta _{l_2 k} \delta _{m_2 n} U_{11,\;L_2 }^\mathrm{F} \left( {r_0 } \right) } &{} {-\delta _{l_2 k} \delta _{m_2 n} U_{12,\;L_2 }^\mathrm{F} \left( {r_0 } \right) } \\ {-\delta _{l_2 k} \delta _{m_2 n} U_{21,\;L_2 }^\mathrm{F} \left( {r_0 } \right) } &{} {-\delta _{l_2 k} \delta _{m_2 n} U_{22,\;L_2 }^\mathrm{F} \left( {r_0 } \right) } \\ \end{array} }} \\ \end{array} }} \right] } \left\{ {{\begin{array}{l} {{\begin{array}{l} {A_{L_2 }^{\mathrm{S}1} } \\ {C_{L_2 }^{\mathrm{S}1} } \\ \end{array} }} \\ {{\begin{array}{l} {D_{L_2 }^\mathrm{F} } \\ {F_{L_2 }^\mathrm{F} } \\ \end{array} }} \\ \end{array} }} \right\} \\ \quad =\left\{ {{\begin{array}{l} {I_{11} \left( {k,n} \right) } \\ {I_{21} \left( {k,n} \right) } \\ {I_{31} \left( {k,n} \right) } \\ {I_{41} \left( {k,n} \right) } \\ \end{array} }} \right\} \\ \end{array} \end{aligned}$$

(81)

in which

$$\begin{aligned} \left\{ {{\begin{array}{l} {I_{11} \left( {k,n} \right) } \\ {I_{21} \left( {k,n} \right) } \\ {I_{31} \left( {k,n} \right) } \\ {I_{41} \left( {k,n} \right) } \\ \end{array} }} \right\} =\mathop {\sum }\limits _{L_1 } {\left( {\mathbf{M}_{L_1 } \left[ {{\begin{array}{l@{\quad }l} {T_{11,\;L_1 }^\mathrm{I} \left( R \right) }&{} {T_{12,\;L_1 }^\mathrm{I} \left( R \right) } \\ {T_{21,\;L_1 }^\mathrm{I} \left( R \right) }&{} {T_{22,\;L_1 }^\mathrm{I} \left( R \right) } \\ {T_{11,\;L_1 }^\mathrm{I} \left( r \right) }&{} {T_{12,\;L_1 }^\mathrm{I} \left( r \right) } \\ {T_{21,\;L_1 }^\mathrm{I} \left( r \right) }&{} {T_{22,\;L_1 }^\mathrm{I} \left( r \right) } \\ \end{array} }} \right] -\left[ {{\begin{array}{l@{\quad }l} {T_{11,\;L_2 }^\mathrm{I} \left( {r_0 } \right) } &{} {T_{12,\;L_2 }^\mathrm{I} \left( {r_0 } \right) } \\ {T_{21,\;L_2 }^\mathrm{I} \left( {r_0 } \right) } &{} {T_{22,\;L_2 }^\mathrm{I} \left( {r_0 } \right) } \\ {U_{11,\;L_2 }^\mathrm{I} \left( {r_0 } \right) } &{} {U_{12,\;L_2 }^\mathrm{I} \left( {r_0 } \right) } \\ {U_{21,\;L_2 }^\mathrm{I} \left( {r_0 } \right) } &{} {U_{22,\;L_2 }^\mathrm{I} \left( {r_0 } \right) } \\ \end{array} }} \right] \mathbf{F}_2 } \right) } \left\{ {{\begin{array}{l} {A_\mathrm{I} } \\ {C_\mathrm{I} } \\ \end{array} }} \right\} \end{aligned}$$

with the Kronecker $\delta _{l_2 k}$ and $\delta _{m_2 n}$.

Let the integer $l_2$ vary from 0 to N (if $\mathop {\sum }\nolimits _{l_2 =0}^N {\mathop {\sum }\nolimits _{m_2 =-l_2 }^{l_2 } }$ is close enough to $\mathop {\sum }\nolimits _{l_2 =0}^\infty {\mathop {\sum }\nolimits _{m_2 =-l_2 }^{l_2 } }$ depending on the accuracy), the number of unknown coefficients to be determined is $4\left( {N+1} \right) ^{2}$. Thus, the system of equations for all unknown coefficients are obtained from Eq. (81) as

$$\begin{aligned} \left[ {{\begin{array}{l} {\tilde{\mathbf{F}}_{0,0} } \\ \vdots \\ {\tilde{\mathbf{F}}_{k,n} } \\ \vdots \\ {\tilde{\mathbf{F}}_{\left( {N+1} \right) ^{2},\left( {N+1} \right) ^{2}} } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {\mathbf{a}_{0,0} } \\ \vdots \\ {\mathbf{a}_{k,n} } \\ \vdots \\ {\mathbf{a}_{\left( {N+1} \right) ^{2},\left( {N+1} \right) ^{2}} } \\ \end{array} }} \right\} =\mathbf{0} \end{aligned}$$

(82)

where

$$\begin{aligned} {\tilde{\mathbf{F}}}_{k,n}= & {} \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {{\varvec{\Omega }}_{0,0} }&{} \cdots &{} {{\varvec{\Omega }}_{k,{} n} }&{} \cdots &{} {{\varvec{\Omega }}_{\left( {N+1} \right) ^{2},\left( {N+1} \right) ^{2}} } \\ \end{array} }} \right] \end{aligned}$$

(83)

$$\begin{aligned} \mathbf{a}_{k,n}= & {} \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {A_{k,n}^{\mathrm{S}1} }&{} {C_{k,n}^{\mathrm{S}1} }&{} {D_{k,n}^\mathrm{F} }&{} {F_{k,n}^\mathrm{F} } \\ \end{array} }} \right] ^{T} \end{aligned}$$

(84)

in which

$$\begin{aligned} {\varvec{\Omega }}_{k,{} n} =\left[ {{\begin{array}{l@{\quad }l} {{\begin{array}{l@{\quad }l} {\delta _{l_2 k} \delta _{m_2 n} T_{11,\;\left( {k,n} \right) }^{\mathrm{S1}} \left( {r_0 } \right) -\tilde{T}_{11,\;\left( {k,n} \right) }^\mathrm{S} \left( R \right) }&{} {\delta _{l_2 k} \delta _{m_2 n} T_{12,\;\left( {k,n} \right) }^{\mathrm{S1}} \left( {r_0 } \right) -\tilde{T}_{12,\;\left( {k,n} \right) }^\mathrm{S} \left( R \right) } \\ {\delta _{l_2 k} \delta _{m_2 n} T_{21,\;\left( {k,n} \right) }^{\mathrm{S1}} \left( {r_0 } \right) -\tilde{T}_{12,\;\left( {k,n} \right) }^\mathrm{S} \left( R \right) }&{} {\delta _{l_2 k} \delta _{m_2 n} T_{22,\;\left( {k,n} \right) }^{\mathrm{S1}} \left( {r_0 } \right) -\tilde{T}_{22,\;\left( {k,n} \right) }^\mathrm{S} \left( R \right) } \\ {\delta _{l_2 k} \delta _{m_2 n} U_{11,\;\left( {k,n} \right) }^{\mathrm{S1}} \left( {r_0 } \right) -\tilde{T}_{13,\;\left( {k,n} \right) }^\mathrm{S} \left( r \right) }&{} {\delta _{l_2 k} \delta _{m_2 n} U_{12,\;\left( {k,n} \right) }^{\mathrm{S1}} \left( {r_0 } \right) -\tilde{T}_{23,\;\left( {k,n} \right) }^\mathrm{S} \left( r \right) } \\ {\delta _{l_2 k} \delta _{m_2 n} U_{21,\;\left( {k,n} \right) }^{\mathrm{S1}} \left( {r_0 } \right) -\tilde{T}_{14,\;\left( {k,n} \right) }^\mathrm{S} \left( r \right) }&{} {\delta _{l_2 k} \delta _{m_2 n} U_{22,\;\left( {k,n} \right) }^{\mathrm{S1}} \left( {r_0 } \right) -\tilde{T}_{24,\;\left( {k,n} \right) }^\mathrm{S} \left( r \right) } \\ \end{array} }}&{} {{\begin{array}{l@{\quad }l} {-\delta _{l_2 k} \delta _{m_2 n} T_{11,\;\left( {k,n} \right) }^\mathrm{F} \left( {r_0 } \right) } &{} {-\delta _{l_2 k} \delta _{m_2 n} T_{12,\;\left( {k,n} \right) }^\mathrm{F} \left( {r_0 } \right) } \\ {-\delta _{l_2 k} \delta _{m_2 n} T_{21,\;\left( {k,n} \right) }^\mathrm{F} \left( {r_0 } \right) } &{} {-\delta _{l_2 k} \delta _{m_2 n} T_{22,\;\left( {k,n} \right) }^\mathrm{F} \left( {r_0 } \right) } \\ {-\delta _{l_2 k} \delta _{m_2 n} U_{11,\;\left( {k,n} \right) }^\mathrm{F} \left( {r_0 } \right) } &{} {-\delta _{l_2 k} \delta _{m_2 n} U_{12,\;\left( {k,n} \right) }^\mathrm{F} \left( {r_0 } \right) } \\ {-\delta _{l_2 k} \delta _{m_2 n} U_{21,\;\left( {k,n} \right) }^\mathrm{F} \left( {r_0 } \right) } &{} {-\delta _{l_2 k} \delta _{m_2 n} U_{22,\;\left( {k,n} \right) }^\mathrm{F} \left( {r_0 } \right) } \\ \end{array} }} \\ \end{array} }} \right] \end{aligned}$$

From Eq. (82), it can be seen that all the coefficients $A_{L_2 }^{\mathrm{S}1}$, $C_{L_2 }^{\mathrm{S}1}$, $A_{L_1 }^{\mathrm{S2}}$, $C_{L_1 }^{\mathrm{S2}}$, $A_{L_1 }^{\mathrm{S3}}$, $C_{L_1 }^{\mathrm{S3}}$, $D_{L_1 }^\mathrm{F}$ and $F_{L_1 }^\mathrm{F}$ are determined for the given expansion term number N.

Similarly, from the boundary conditions (49) and (51), the coefficients $B_{L_2 }^{\mathrm{S}1}$, $B_{L_1 }^{\mathrm{S2}}$, $B_{L_1 }^{\mathrm{S3}}$ and $E_{L_2 }^{\mathrm{S}1}$ could be solved by the following process. The total equations are formed that

$$\begin{aligned} \begin{array}{l} \left( {\left\{ {{\begin{array}{l} {T_{31,\;L_2 }^{\mathrm{S1}} \left( {r_0 } \right) } \\ {U_{31,\;L_2 }^{\mathrm{S1}} \left( {r_0 } \right) } \\ \end{array} }} \right\} -\mathop {\sum }\limits _{L_2 } {\mathop {\sum }\limits _{L_1 } {\left[ {{\begin{array}{l@{\quad }l} {T_{31,\;L_2 }^{\mathrm{S2}} \left( {r_0 } \right) }&{} {T_{31,\;L_2 }^{\mathrm{S3}} \left( {r_0 } \right) } \\ {U_{31,\;L_2 }^{\mathrm{S2}} \left( {r_0 } \right) }&{} {U_{31,\;L_2 }^{\mathrm{S3}} \left( {r_0 } \right) } \\ \end{array} }} \right] \mathbf{F}_1 \left[ {{\begin{array}{l@{\quad }l} {T_{51,\;L_1 }^{\mathrm{S2}} \left( R \right) }&{} {T_{51,\;L_1 }^{\mathrm{S3}} \left( R \right) } \\ {T_{51,\;L_1 }^{\mathrm{S2}} \left( r \right) }&{} {T_{51,\;L_1 }^{\mathrm{S3}} \left( r \right) } \\ \end{array} }} \right] ^{-1}\left\{ {{\begin{array}{l} {T_{51,\;L_1 }^{\mathrm{S}1} \left( R \right) } \\ {T_{51,\;L_1 }^{\mathrm{S}1} \left( r \right) } \\ \end{array} }} \right\} } } } \right) B_{L_2 }^{\mathrm{S}1} \\ \quad -\left\{ {{\begin{array}{l} {T_{31,\;L_2 }^\mathrm{F} \left( {r_0 } \right) } \\ {U_{31,\;L_2 }^\mathrm{F} \left( {r_0 } \right) } \\ \end{array} }} \right\} E_{L_2 }^\mathrm{F} =0 \\ \end{array} \end{aligned}$$

(85)

Also, it can be seen that Eq. (85) are tenable for any incident frequency and N, and this indicates that all the constants $B_{{L}'}^{22}$, $\tilde{B}_L^{11}$, and $E_{{L}'}^{22}$ are equal to zero.