Bimaterial infinite plane with a cavity on the interface subjected to different temperatures

Abstract

Stress analysis is applied to two bonded materials of infinite extent with a single notch at their interface. The two materials, represented in normal view as two joined half planes with a notch, are subjected to different temperatures. As illustration, a bimaterial infinite plane with an elliptical hole at the interface is analyzed. To achieve a closed-form solution, a rational mapping function and a complex variable method are used. By changing the mapping function, other geometries for the notch can be analyzed. The cavity at the interface constitutes a small defect because its extent is small compared with the infinite plane. A mathematical difficulty arises with the presence of the points at infinity of the half planes. The coefficients of the homogeneous part of the stress function are expressible in terms of Dundurs’ parameters, but the temperature-dependent loading term is not. Stress distributions without and with debonding for two pairings of bimaterial are shown. The stress intensity of debonding is defined, and values are investigated for various debonding lengths for the elliptical holes. Also the debonding extension is investigated. As a special case, the stress intensity factors for T-shaped cracks are also investigated.

1 Introduction

For the past few decades, problems directly related to bonded dissimilar materials have been of interest because they have become prominent in a wide range of applications where different materials are used. The analyses of stress behavior of these bonded bimaterial are more complicated than those of homogeneous materials. Establishing analytical methods to ascertain mechanical strength is important as is knowing also the fracture behavior at debonded crack tips. Many bimaterial problems have been solved in [1–7] and references therein. Also many references are listed in handbooks [8–10]. Advances on the subject have been reported in [11–16]. Studies of problems involving the bending of thin plates subjected to temperatures have been reported in [17, 18]. An analysis of bonded half planes with a cavity or a rigid inclusion at the interface subjected to uniform tension has appeared in [19–21]. For a Green’s function analysis of the interaction between a crack and a cavity or inclusion, various studies have been reported in [22–25].

Indeed, with regard to bonded dissimilar materials, it appears possible to derive general solutions in closed-form. A cavity is one type of defect at an interface from where fractures start; therefore, stress analysis of the fracture is important.

In the present paper, half planes of the bonded dissimilar materials with a cavity at the interface (with an elliptical hole used as illustration) subjected to different temperatures are analyzed. Temperature or thermal loading is one of the typical forms of loading which include mechanical loading. To achieve a closed-form solution, a rational mapping function and a complex stress function method are used. In solving the problem, the thickness of the bond is not considered, that is, the thickness is assumed to be zero. The general solution of this temperature problem for bonded half planes with a cavity appears not to have been derived. Other geometries can be analyzed by changing the mapping function. The mapping function of the half plane includes the points at infinity which lie on the unit circle of the mapping function. This fact presents a slight difficulty in the derivation. Stress intensities of debonding (SIDs) as well as stress distributions are obtained. The SID is used to evaluate the mechanical intensity of a debonding tip and correspond to the square root of the strain energy release rate. Thus, the evaluation of the intensity of debonding using SID is the same as that using the strain energy release rate. The possibility of the debonding site being extended and a crack entering the material are also investigated. As a special case, stress intensity factors for T-shaped cracks are also investigated.

2 Preparation for analysis

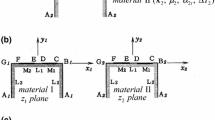
As a demonstration, an analysis of stresses is applied to a bimaterial of infinite extent with an elliptical hole and with debondings on the interface (see Fig. 1a). The structure is composed of two half planes attributed with dissimilar material properties, representing materials I and II, respectively, each with a semi-elliptical notch joined at the bimaterial interface. The notch has a symmetrical shape with respect to the straight-line interface. The width of the elliptical notch, its depth, and the unbonded segments on the right- and left-hand sides of the notch are denoted by $a, b, c_{1}$, and $c_{2}$, respectively. The unbonded segments are modeled when debonding has occurred and hereafter are called the debonding sites; their lengths are the debonding lengths. When $a=0, b\ne 0$, a T-shaped crack appears if $c_1\ne 0, \hbox {c}_{2}=0$, and a cross-shaped crack appears if $c_1 \ne 0,\hbox {c}_2 \ne 0$. When $a\ne 0, b=0$, an interfacial crack is obtained. The materials I and II of the half plane are subjected to different uniform temperatures, $\Delta T_1$ and $\Delta T_2$, respectively, which represent the increase from the room temperature. The coefficients of linear expansion for temperature are denoted by $\alpha _{1}$ and $\alpha _{2}$ for materials I and II, respectively. Contact between materials I and II at debonding sites is not considered when the temperatures are applied. Components of stress and displacement are continuous on the interface. It is assumed that the shear modulus, Poisson’s ratio, and coefficient of linear expansion for temperature are not changed by temperature change.

Fig. 1

Bonded half planes with notches. a Physical planes, b analytical planes, c unit circles

The coordinates shown in Fig. 1a are denoted by (X, Y). This plane is called the physical plane. When material I is rotated about the X-axis, the $z_{1}$ plane in Fig. 1b is obtained. The $z_{1}$ and $z_{2}$ planes of Fig. 1b are called analytical planes, and their coordinates are denoted by $(x_{j}, y_{j})$, where suffices $j=1, 2$ account for materials I and II, respectively. These shapes are mapped inside the unit circle (Fig. 1c) by the same mapping function, because the shapes of materials I and II on the $z_{1}$ and $z_{2}$ planes are identical. In regard to notation and suffices of the coordinates, components of stress and displacement on the physical plane in Fig. 1a are in upper case letters, whereas those on the coordinates in Fig. 1b are in lower case letters. The boundaries of interface shown in Fig. 1a, b are denoted by M and the other boundaries by $L_{j}$ ($j=1,2$). The components of displacement and stress in Fig. 1a, b are related as follows:

$$\begin{aligned} U_{1}= & {} u_1 \quad V_{1}=-v_1 \quad U_2 =u_2 \quad V_2 =v_2 \nonumber \\ \sigma _{X1}= & {} \sigma _{x1} \quad \sigma _{Y1} =\sigma _{y1} \quad \tau _{XY1} =-\tau _{xy1} \nonumber \\ \sigma _{X2}= & {} \sigma _{x2} \quad \sigma _{Y2} =\sigma _{y2} \quad \tau _{XY2} =\tau _{xy2} . \end{aligned}$$

(1)

The components of stress and displacement on the analytical planes in Fig. 1b are first calculated, and then those in the physical plane in Fig. 1a can be obtained using Eq. (1).

The point at infinity is assumed not to be constrained.

3 Material constants

The material constants are expressed using Dundurs’ parameters $\alpha _\mathrm{D}$ and $\beta _\mathrm{D}$ as follows [26]:

$$\begin{aligned} \alpha _{D}= & {} \frac{\left( \kappa _1 +1\right) \Gamma -(\kappa _2 +1)}{(\kappa _1 +1)\Gamma +(\kappa _2 +1)}, \end{aligned}$$

(2a)

$$\begin{aligned} \beta _\mathrm{D}= & {} \frac{\left( \kappa _1 -1\right) \Gamma -(\kappa _2 -1)}{(\kappa _1 +1)\Gamma +(\kappa _2 +1)}, \end{aligned}$$

(2b)

$$\begin{aligned} \Gamma= & {} \frac{\mu _2}{\mu _1}, \end{aligned}$$

(2c)

where $\mu _j\;(j=1,2)$ is the shear modulus, $\kappa _{j}\;(j=1,2)$ is $(3-\nu _j )/(1+\nu _j )$ for the plane stress state and $3-4\nu _j$ for the plane strain state, and $\nu _j (j=1,2)$ is Poisson’s ratio for materials I and II, respectively. If materials I and II have the same properties (homogenous case), then $\alpha _\mathrm{D}=\beta _\mathrm{D} =0$. The constraints $-1.0\le \alpha _\mathrm{D}\le 0$ and $\mu _2\le \mu _1$ are assumed because the analysis is performed for a symmetric shape. When $\alpha _\mathrm{D} =-1.0$, materials I and II are rigid and elastic, respectively, but vice versa if. Some parameters are denoted here, which will be used later:

4 Mapping function

A mapping function that maps a half plane with a semi-elliptic notch onto a unit circle takes form

$$\begin{aligned} z_j =-ib\sqrt{2}\frac{\sqrt{1+t_j ^{2}}}{1-t_j }-ia\frac{1+t_j}{1-t_j}. \end{aligned}$$

(4)

where $t_j =1$ corresponds to infinity.

Constants a and b in the equation above are the semimajor and semiminor axes of the ellipse along the $x_{j}$ and $y_{j}$ axes, respectively. Because Eq. (4) is not a rational function, a rational mapping function is, nevertheless, obtainable,

$$\begin{aligned} z_{j}= & {} -ib\sqrt{2}\frac{\sqrt{1+t_j ^{2}}}{1-t_j }-ia\frac{1+t_j }{1-t_j } \nonumber \\= & {} -ib\frac{\sqrt{2}}{1-t_j }\left[ {1+\sum _{j=1}^{14} {\left( {\frac{-A_j }{1+\alpha _j t_j^2 }+A_j}\right) }} \right] -ia\frac{1+t_j }{1-t_j}\quad (j=1,2) \nonumber \\\equiv & {} \frac{E_0 }{1-t_j }+\sum _{k=1}^N {\frac{E_k}{\zeta _k -t_j}}+E_{c} \end{aligned}$$

(5)

where $E_{0}, E_k, E_c$, and $\zeta _{k}$ are complex constants. The accuracy of $A_j, \alpha _{j}$ for j = 1–14 was stated in the Refs. [1–3] and have been obtained in Refs. [1–3, 27], and $N=14\times 2=28$ is used in this analysis. The procedures used in computations for obtaining the constants in Eq. (5) are explained in detail in Hasebe and Wang [28] and Wang and Hasebe [29].

5 Analytical method

The analytical method for different temperatures was described in [4], but is different from the present problem as the mapping function (5) includes the term $E_0 /(1-t_j )$ corresponding to infinity. The pole $t_j =1$ exists on the unit circle and causes a complication in deriving the analytical solution. This analytical solution is a general solution for the bimaterial infinite plane. The complex stress functions are expressed as $\phi _j (t_j)$ and $\psi _{j} (t_j)\quad (t_j =1,2)$ denoted by variables $t_j (j=1,2)$ in the unit circle.

When given a boundary without an external force present, $\psi _{j} (t_j )$ is expressed using analytical continuation [30],

$$\begin{aligned} \psi _j (t_j )=-\overline{\phi _j (1/\overline{t_j })} -\frac{\overline{\omega (1/\overline{t_j})}}{{\omega }'(t_j)}{\phi }'_j (t_j) \end{aligned}$$

(6)

The stress function $\phi _j (t_j )$ is determined by solving the Riemann–Hilbert problem [4],

$$\begin{aligned} \phi _j (t_j )=H_j (t_j )+\frac{\chi _j (t_j )}{2\pi i}\int \limits _M {\frac{\gamma _j g_j (\sigma )}{\chi _j (\sigma )(\sigma -t_j )}\hbox {d}\sigma } +\chi _j (t_j)P_j (t_j) \end{aligned}$$

(7)

where $H_j (t_j )$ is the loading term to be determined below, and $\chi _j (t_j)$ is the Plemelj function:

where $\alpha , \beta$ are the coordinates at the juncture of the boundaries $L_j$ and M. $\lambda _j$ is given by Eq. (3), and the following conditions hold:

The unknown rational function $P_j (t_j )$ is written [4]

$$\begin{aligned} P_j (t_j )=-\sum _{k=1}^N {\frac{\overline{A_{jk}}B_k}{\chi _{j} \left( \zeta _k\right) \left( \zeta _k -t_j\right) }}, \end{aligned}$$

(10)

where the unknown coefficients $A_{jk}$ are given by the relation $A_{jk} ={\phi }'_j ({\zeta }'_k )$ to be determined later, and $B_k$ is denoted by $B_k \equiv E_k /\overline{{\omega }'({\zeta }'_k)}$. The unknown rational function $g_i (t_j)$ in Eq. (7) is assumed to be a regular function in regions $S_j^+$ and $S_j^-$ [see Fig. 1c], respectively, with a first-order pole at $t_j =1$ on the unit circle. Hence,

$$\begin{aligned} g_j (t_j )=\sum _l{\frac{a_{jl} }{\xi _{jl} -t_j}}+\sum _l {\frac{b_{jl} }{\eta _{jl} -t_j }} +\frac{d_j}{1-t_j} \end{aligned}$$

(11)

where $a_{jl}, b_{jl}, \xi _{jl}, \eta _{jl}$, and $d_j$ are undetermined complex constants, and $\left| \xi _{jl}\right| >1$, $\left| \eta _{jl}\right| <1$ are assumed. The integral term in Eq. (7) is transformed as follows:

$$\begin{aligned}&\frac{\chi _j (t_j )}{2\pi i}\int \limits _M {\frac{\gamma _j g_j (\sigma )}{\chi _j (\sigma )(\sigma -t_j )}\hbox {d}\sigma } \nonumber \\&\quad =\frac{\chi _j (t_j )}{2\pi i}\frac{\gamma _j }{1+\lambda _j }\oint \limits _M {\frac{g_j (\sigma )}{\chi _j (\sigma )(\sigma -t_j )}} \hbox {d}\sigma \nonumber \\&\quad =\frac{\gamma _j }{1+\lambda _j }\left[ {\sum _l {\left\{ {1-\frac{\chi _j (t_j )}{\chi _j (\xi _{jl} )}} \right\} \frac{a_{jl} }{\xi _{jl} -t_j }+\sum _l {\left\{ {1-\frac{\chi _j (t_j )}{\chi _j (\eta _{jl} )}} \right\} \frac{b_{jl} }{\eta _{jl} -t_j }+\left\{ {1+\frac{1-\lambda _j}{2}\frac{\chi _j (t_j )}{\chi _j (1)}} \right\} \frac{d_j }{1-t_j}}}}\right] \nonumber \\ \end{aligned}$$

(12)

where the second line is a contour integration around M, and the third line is obtained using the residue theorem. The integral includes the coordinate $t_j =1$, and the residue theorem must be used by considering the relations in Eq. (9). Substituting Eq. (12) into Eq. (7), the stress solution is expressed as

$$\begin{aligned}&\phi _j (t_j)=H_j (t_j) \nonumber \\&\quad +\,\frac{\gamma _j }{1+\lambda _j}\left[ {\sum _l {\left\{ {1-\frac{\chi _j (t_j )}{\chi _j(\xi _{jl})}} \right\} \frac{a_{jl} }{\xi _{jl} -t_j }+\sum _l {\left\{ {1-\frac{\chi _j (t_j)}{\chi _j (\eta _{jl} )}} \right\} \frac{b_{jl}}{\eta _{jl} -t_j }+\left\{ {1+\frac{1-\lambda _j }{2}\frac{\chi _j (t_j )}{\chi _j (1)}} \right\} \frac{d_j}{1-t_j}}}}\right] \nonumber \\&\quad -\,\chi _j (t_j )\sum _{k=1}^N {\frac{\overline{A_{jk} } B_k }{\chi _j (\zeta _k )(\zeta _k -t_j )}} \end{aligned}$$

(13)

where the loading term $H_j (t_j )$ is given by [4]

$$\begin{aligned} H_j (t_j )=\frac{\chi _j (t_j )}{2\pi i}\int \nolimits _M {\frac{h_{jM} (\sigma )}{\chi _j (\sigma )(\sigma -t_j )}} \hbox {d}\sigma . \end{aligned}$$

(14)

For thermal loading, uniform temperatures $\Delta T_1$ and $\Delta T_2$ are applied to materials I and II, respectively. It is assumed that the displacements are not constrained at points of infinity. The temperature gives the displacement components on M, that is, $u_j^{(b)} =-\alpha _j^{*} \Delta T_j x_j$ and $v_j^{(b)} =0$ at $x_1 =x_2$ on the interface, where $\alpha _j^{*}$ is $\alpha _j^{*} =\alpha _j$ for the plane stress state and $\alpha _j^{*} =(1+\nu _j )\alpha _j$ for the plane strain state.

The term $h_{1M} (\sigma )$ given by the boundary condition on M is expressed as

$$\begin{aligned} h_{1M} (\sigma )=2\frac{\mu _2 \gamma _1 }{\kappa _2 +1}(\alpha _2^{*} \Delta T_2 -\alpha _1^{*} \Delta T_1 )x_1 . \end{aligned}$$

(15)

The interface is a straight line and the following relation holds on M because $y_j =0$,

$$\begin{aligned} x_j =\hbox {Re}[z_j ]=\hbox {Re}[\omega (\sigma )]=\frac{\omega (\sigma )+\overline{\omega (\sigma )} }{2}=\omega (\sigma ) \end{aligned}$$

(16)

Substituting Eqs. (15) and (16) using $\omega (\sigma )$ into Eq. (14), the loading term is written

$$\begin{aligned} H_1 (t_1 )= & {} 2\frac{\mu _2 \gamma _1 }{\kappa _2 +1}(\alpha _2^{*} \Delta T_2 -\alpha _1^{*} \Delta T_1 )\frac{\chi _1 (t_1 )}{2\pi i}\int \limits _M {\frac{\omega (\sigma )}{\chi _1 (\sigma )(\sigma -t_1 )}\hbox {d}\sigma } \nonumber \\= & {} 2\frac{\mu _2 \gamma _1 }{\kappa _2 +1}(\alpha _2^{*} \Delta T_2 -\alpha _1^{*} \Delta T_1 )\frac{1}{1+\lambda _1 }\frac{\chi _1 (t_1 )}{2\pi i}\oint \limits _M {\frac{\omega (\sigma )}{\chi _1 (\sigma )(\sigma -t_1 )}\hbox {d}\sigma } \end{aligned}$$

(17)

Changing the line integral along M to a contour integration around M (Fig. 2) and using the residue theorem, the loading term $H_j (t_j)$ becomes

Fig. 2

Circuit integration around M

If the third equality of Eq. (16) is used, Eq. (18a) can be expressed alternatively by Eq. (43) given in Appendix.

The coefficient of the loading term has the dimensions of $\mu _2$ ($\kappa _1 , \kappa _2$ are dimensionless); therefore, the coefficient is not expressible by dimensionless Dundurs’ parameters $\alpha _\mathrm{D}$ and $\beta _\mathrm{D}$.

Next, the unknown coefficients $a_{jl}$, $b_{jl}$, $\xi _{jl}$, $\eta _{jl}$, and $d_j$ in Eq. (11) are determined [4], using the following relations:

where ${\xi }'_{21} \equiv 1/\bar{{\xi }}_{21}$ and ${\eta }'_{21} \equiv 1/\bar{{\eta }}_{21}$.

Finally, the following relations are obtained:

For material II, the same procedure is repeated and the coefficients are expressed by exchanging suffices $j=1$ and 2.

The general solution for $\phi _j (t_j )$, Eq. (7), is expressed as

The unknowns $A_{jk} (j=1,2, k=1,2,\ldots ,N)$ are determined from the condition $A_{jk} ={\phi }'_j ({\zeta }'_k )$. When ${\zeta }'_k$ are substituted into the first derivative of Eq. (21) for $j=1$ and 2, linear equations for $A_{jk}$ and $\bar{{A}}_{jk}$ ($j=1,2$) are obtained. Solving the 4N set of simultaneous linear equations for their real and imaginary parts, all $A_{jk}$ are determined.

The solutions for particular material constants are investigated.

(a) Homogenous materials I and II, and different temperatures.

The material constants: $\alpha _\mathrm{D} =\beta _\mathrm{D} =0$, $\lambda _j =1$, $\gamma _j /(1+\lambda _j )=1/2 (j=1,2)$, $(1+\lambda _j -\gamma _j )/\gamma _j =1 (j=1,2)$, Plemelj function $\chi _j (t_j )=(t_j -\alpha )^{0.5}(t_j -\beta )^{0.5}$ where $\varepsilon _j =0$ [see Eq. (8b)].

$\Lambda _j =\mu _2 (\alpha _{(3-j)}^{*} \Delta T_{(3-j)} -\alpha _j^{*} \Delta T_j )/[2(\kappa _2 +1)]$ where $\mu _1 =\mu _2 , \kappa _1 =\kappa _2$.

The solutions yield the following:

(b) Materials I and II are rigid and elastic, respectively.

The material constants: $\mu _1 =\infty , \nu _1 =0, \alpha _1^{*} =0, \alpha _\mathrm{D} =-1, \beta _\mathrm{D} =-(\kappa _2 -1)/(\kappa _2 +1)$.

(c) Interfacial crack $(a\ne 0, b=0)$,

In Eq. (5), $E_k =0 (k=1,2,\ldots ,N) B_k =0$

$$\begin{aligned} \phi _j (t_j )=H_j (t_j )=2\Lambda _j \left[ {\left( {1+\frac{1-\lambda _j }{2}\frac{\chi _j (t_j )}{\chi _j (1)}} \right) \frac{E_0 }{1-t_j }} \right] \end{aligned}$$

(25)

$\Lambda _j$ is denoted by Eq. (18b).

6 Stress distributions

The stress components on the $z_j$ plane (analytical plane) are given as:

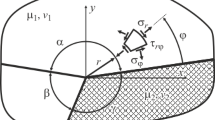
In curvilinear coordinates, the stress components $\sigma _{rj}$, $\sigma _{\theta j}$, and $\tau _{r\theta j}$ in terms of the mapping function $\omega (t_j )$ are expressed by $\sigma _{xj} ,\sigma _{yj}$, and $\tau _{xyj}$ as follows:

The stress components on the physical plane are obtained using Eq. (1).

Along the interface M, the stress components satisfy:

For a given temperature, the following relation also holds on the interface M [4]:

$$\begin{aligned} \sigma _{X2} =\mu \sigma _{X1} +\gamma \sigma _Y +\frac{16}{\alpha _\mathrm{D} -1}\Lambda _1 \end{aligned}$$

(29)

Fig. 3

a Stress distributions of material I (Fe) for $b/a=1$ without debondings (material II, Cu). b Stress distributions of material II (Cu) for $b/a=1$ without debondings, (material I, Fe)

Dividing the equation above by $\Lambda _1$, it is noticed that Eq. (29) is not related by $\Lambda _1$. $\mu$ and $\gamma$ are given by Eq. (3e, j).

The stress function vanishes, $\phi _j (t_j )=0$, when conditions

$$\begin{aligned} \alpha _2^{*} \Delta T_2 -\alpha _1^{*} \Delta T_1 =0 \end{aligned}$$

(30)

hold, and therefore, stresses are not present.

Figure 3a and b shows the stress distributions for the upper and lower half planes with semicircular notch, respectively. The materials I and II are iron (Fe) and copper (Cu), respectively, and the Dundurs’ parameters are $\alpha _\mathrm{D} =-0.233$ and $\beta _\mathrm{D} =-0.064$. The stress components are non-dimensionalized by $\left| \Lambda _{j}\right|$. However, note that $\Lambda _1 =-\Lambda _2$ holds. The plane stress state is shown and is confirmed from the analytical results for which Eqs. (28) and (29) hold. The range of influence of the elliptical hole on the stress distributions on the boundary for materials I and II is roughly in the range $-2<X/a<2$. At the tip of the hole, large stresses arise. The normal stress component $\sigma _r (=\sigma _Y )$ on M away from the elliptical hole is very small compared with other stress components; therefore, the debonding extension for the opening seems to be difficult and the debonding extension due to shear stress $\tau _{XY}$ or a crack initiation into the material due to $\sigma _X$ may occur. Figures 4a, b and  5a, b show the stress distributions on the boundary with debonding lengths $c_1 /a=1$, $c_2 /a=0$, for $b/a=1$, and $b/a=2$, respectively. No significant differences between these distributions appear.

Fig. 4

a Stress distributions of material I (Fe) for $b/a=1$ and $c_{1}/a=1, c_{2}/a=0$ (material II, Cu). b Stress distributions of material II (Cu) for $b/a=1$ and $c_{1}/a=1, c_{2}/a=0$ (material I, Fe)

Fig. 5

a Stress distributions of material I (Fe) for $b/a=2$ and $c_{1}/a=1, c_{2}/a=0$ (material II, Cu). b Stress distributions of material II (Cu) for $b/a=2$ and $c_{1}/a=1, c_{2}/a=0$ (material I, Fe)

7 Stress intensity of debonding

The expressions that represent the stress components on the interface close to the tip of debonding are investigated. The coordinate system shown in Fig. 6 is assumed; the material for which $Y_n \ge 0$ is labeled material A, and that for which $Y_n \le 0$ is labeled material B.

Fig. 6

Coordinates system near the debonding tip

The expressions for the stress near point E in Fig. 1a are derived. Then, material A may be deemed to be material I, and material B to be material II. Point $E \quad (z_j =z_E )$ corresponds to point $t_j =\beta$ on the $t_j$ plane. When the first derivative of the stress function is expanded around point $z_j=z_E$, the first term that is singular in Eq. (21) is expressed in the form

$$\begin{aligned} {\Phi }'_j (z_j )=\frac{K_E^{(j)} \exp \left( \pi \varepsilon _j \right) }{2\sqrt{2\pi }}(z_j -z_E )^{-m_j}+O(r^{0}), \end{aligned}$$

(31)

where $\varepsilon _{j}$ is the imaginary part of $m_j$ (see Eq. 8b), and $\varepsilon _1 =-\varepsilon _2$ from Eq. (3).

This leads to expression for the stress components on the interface $(\theta =0)$ near point E

where $\tau _{XYj}$ is positive when $j=1$ and negative when $j=2$. The complex number $K_E^{(j)}$ is expressed as $K_E^{(j)} \equiv K_{EI}^{(j)} +iK_{EII}^{(j)}$ corresponding to complex stress intensity factors (SIFs), and $\Theta _E^{(j)}$ is the argument of $K_E^{(j)}$. Because Eq. (28) holds on M, then $K_E^{(1)} =\overline{K_E^{(2)} }$ holds. The stress distribution extremely near the tip of debonding oscillates because of the term $\varepsilon _j \ln (r)$ in the trigonometric functions and becomes infinite on approaching the tip of debonding.

In representing the stresses near point F in Fig. 1a, materials A and B in Fig. 6 are deemed to be materials II and I, respectively. Point $F \quad (z_j =z_F )$ corresponds to point $t_j =\alpha$ on the $t_j$ plane. When the first derivative of the stress function is expanded around point $z_j =z_F$, its first term, which is singular, can be represented as

$$\begin{aligned} {\Phi }'_j (z_j )=\frac{K_F^{(j)} \exp (\pi \varepsilon _j )}{2\sqrt{2\pi }}(z_j -z_F )^{m_j -1}+O(r^{0}). \end{aligned}$$

(33)

$K_F^{(j)}$ is a complex number, $K_F^{(j)} \equiv K_{FI}^{(j)} +iK_{FII}^{(j)}$, corresponding to the complex SIFs. From Eq. (33), the stress components on the interface $(\theta =0)$ near point F are given by

where $\tau _{XYj}$ is positive for $j=1$ and negative for $j=2$, and $\Theta _F^{(j)}$ is the argument of $K_F^{(j)}$. Because Eq. (28) holds on M, $K_F^{(1)} =\overline{K_F^{(2)} }$ holds. Again, the stress distribution extremely near the tip of debonding oscillates because of the term $\varepsilon _j \ln (r)$ in the trigonometric functions and the stress becomes infinite on approaching the tip of debonding.

The strain energy release rate G for debonding extension is given by [31, 32]:

$$\begin{aligned} G=\frac{1}{16}\left( {\frac{\kappa _1 +1}{\mu _1 }+\frac{\kappa _2 +1}{\mu _2 }} \right) K^{(j)}\overline{K^{(j)}}. \end{aligned}$$

(35)

The notation $K^{(j)}$ means $K_E^{(j)}$ when point E is intended at the tip of debonding and $K_F^{(j)}$ when point F is intended. From Eqs. (32) and (34), near the tip of debonding, the magnitude is $\sqrt{K^{(j)}\overline{K^{(j)}} }$. Accordingly, we refer to it as the “stress intensity of debonding (SID).” Note from Eq. (35) that the evaluation of the stress intensity at the tip of debonding using the SID is the same as that using the strain energy release rate G. In this interpretation, the SID give one parameter for evaluating the strength with respect to debonding for $\sigma _Y$, with respect to slippage for $\tau _{XY}$ and with respect to crack initiation into the material for $\sigma _{Xj} (j=1, 2)$.

The method of calculating the SID using the complex stress function (21) is described. The first derivative of the complex stress function is decomposed into a term that includes the Plemelj function and a term that does not, i.e.,

$$\begin{aligned} {\phi }'_j (t_j )=\frac{\chi _j (t_j )}{(t_j -\alpha )(t_j -\beta )}J_j (t_j )+J_j^0 (t_j ). \end{aligned}$$

(36)

Applying $J_j (t_j )$ in Eq. (36) and the mapping function $\omega (t_j )$, for point $t_j =\beta$ (point E), $K_E^{(j)}$ is

calculated by [33]

$$\begin{aligned} \frac{K_E^{(j)} \exp (\pi \varepsilon _j )}{2\sqrt{2\pi }}=\frac{\left| {{\omega }'(\beta )(\beta -\alpha )} \right| ^{m_j }}{{\omega }'(\beta )(\beta -\alpha )}J_j (\beta )\exp \left[ {-im_j (\pi +\rho /2)} \right] \end{aligned}$$

(37)

and $K_F^{(j)}$ for point $t_j =\alpha$ (point F) is

$$\begin{aligned} \frac{K_F^{(j)} \exp (\pi \varepsilon _j )}{2\sqrt{2\pi }}=\frac{\left| {{\omega }'(\alpha )(\alpha -\beta )} \right| ^{1-m_j }}{{\omega }'(\alpha )(\alpha -\beta )}J_j (\alpha )\exp \left[ {i(1-m_j )(\pi +\rho /2)}\right] , \end{aligned}$$

(38)

where the angle $\rho =\angle \alpha 0\beta$ (0 is the center of unit circle, see Fig. 1c).

To analyze the actual phenomena at the tip of debonding, a dimensionless parameter N is defined,

$$\begin{aligned} N=\frac{1}{\left| {\Lambda _j}\right| \sqrt{a}}\sqrt{K^{(j)}\overline{K^{(j)}}}. \end{aligned}$$

(39)

From $\Lambda _1 =-\Lambda _2$, we assume that $\Lambda _1$ is positive in the following; therefore, $\Lambda _2 <0$.

Figures 7 and 8 show N values for some elliptical holes and bimaterial pairings Fe with Cu, and Fe with Al, respectively (see Table 1). When $c_1 /a=0$ for $b/a=0$ (interfacial crack), N takes finite values, but N is zero for $b/a\ne 0$. There are extreme values or elliptical holes, and they are larger when b / a are larger. When $c_1 /a$ becomes infinite, N approaches a constant value. To avoid debonding extension or incursion into the material, the fracture toughness value of debonding must be set larger than the maximum values. It is assumed that the influence of the thickness of the bond may be included in the fracture toughness value.

Fig. 7

N values versus debonding lengths $c_{1}$/a for some b / a values: $c_{2}/a=0$, material I, Fe and material II, Cu

Fig. 8

N values versus debonding lengths $c_{1}$/a for some b / a values: $c_{2}/a=0$, material I, Fe and material II, Al

Table 1 Material constants

When the width of the elliptical hole becomes zero $(a=0)$ and the debonding $c_1 \ne 0$ and $c_2 =0$, a T-shaped crack is obtained. The SID at the tip E are investigated, and for this purpose, dimensionless SID are defined:

$$\begin{aligned} N_E =\frac{1}{\left| {\Lambda _j} \right| \sqrt{b}}\sqrt{K_{^{E}}^{(j)}\overline{K_{^{E}}^{(j)} } }. \end{aligned}$$

(40)

Figure 9 shows $N_{{E}}$ values for bimaterial Fe with Cu, and Fe with Al. Values $N_{{E}}$ also take maximum values around $c_1 /b=0.8{\sim }0.9$. Thereafter, the values $N_{{E}}$ decrease rapidly for increasing $c_1 /b$ and then start to increase. Therefore, debonding does not extend when the respective fracture toughness values are larger than the maximum values.

Fig. 9

$N_{E}$ values versus debonding lengths $c_{1}/b$: $c_{2}/b=0$, material I, Fe and material II, Cu or Al

8 Stress intensity factor

When the width of an elliptical hole is zero $(a=0)$, a T-shaped $(c_1 \ne 0, c_2 =0)$ or a cross-shaped $(c_1 \ne 0, c_2 \ne 0)$ crack is obtained. The stress intensity factor (SIF) for the crack is calculated using [23]

$$\begin{aligned} K_{\mathrm{I}j} -iK_{\mathrm{II}j} =2\sqrt{\pi }e^{-i\frac{\delta _j }{2}}\frac{{\phi }'_j (\zeta _0 )}{\sqrt{{\omega }''(\zeta _0 )}}\quad (j=1,2), \end{aligned}$$

(41)

where $\delta _j$ is the angle between the direction of the crack and the x-axis, and $\zeta _0$ the coordinates of the crack tip. In the present paper, $\zeta _0 =-1$ and $\delta _j =\pi /2$.

The T-shaped crack is investigated. The following dimensionless SIF is defined,

$$\begin{aligned} F_{\mathrm{I}j} +iF_{\mathrm{II}j} ={\left( {K_{\mathrm{I}j} +iK_{\mathrm{II}j} } \right) }/{\sqrt{\pi b}}\quad (j=1,2). \end{aligned}$$

(42)

Figure 10 shows the SIF values for bimaterial pairs Fe with Cu, and Fe with Al. Mode II SIF $F_{\mathrm{II}j}$ values are larger than those of Mode I SIF $F_{\mathrm{I}j}$. The SIFs increase when the debonding length is around $c_1 /b=5$ and take constant values thereafter.

Fig. 10

Non-dimensional SIF $F_{\mathrm{I}}$ and $F_{\mathrm{II}}$ values versus debonding lengths $c_{1}/b$: $c_{2}/b=0$, material I, Fe and material II, Cu or Al

9 Conclusions

An analytic solution was derived to the problem of two dissimilar materials bonded at their interface for a half plane with a notch subject to thermal loading. It was assumed that the displacements are not constrained at infinity. Problems involving bonded dissimilar materials with different notches also can be analyzed by changing the coefficients in the mapping function Eq. (5), as for example, a half plane with a triangular notch or notch with a crack (Hasebe and Iida [34]). For half-plane shapes, the mapping function is infinite at $t_i =1$ with infinity being mapped onto the unit circle. The stress function is denoted by Eq. (21). The coefficients of the homogenous solution $P_j (t_j )$ in the stress function are expressed in terms of Dundurs’ parameters, but this is not true for the loading term associated with temperature. Some stress distributions were shown. When condition (30) is satisfied, the stresses vanish. The $\sigma _Y$ on the interface is very small; therefore, the extension of debonding because of $\sigma _Y$ may be difficult. The extension arises from $\tau _{XY}$ or a crack initiation into material I from $\sigma _{X1}$ for $\Lambda _1 >0$ or material II from $\sigma _{X2}$ for $\Lambda _2 >0$ is apt to occur. The values for SID are precisely calculated directly from $\omega (t_j )$ and $\phi _j (t_j )$ without using any other numerical techniques. The SID is equivalent to a strain energy release rate used in evaluating the strength of the debonding. The N values of the SID for debonding from elliptical holes take extreme values with increasing $c_1 /a$; therefore, when the N values for the fracture toughness value of debonding is larger than the extreme value, debonding does not extend further. If the fracture toughness value is smaller than the extreme value, debonding stops at a certain debonding length. When the N value also takes a maximum value, crack at the debonding tip is apt to be initiated and propagate into the material. When $c_1 \ne 0, c_2 =0$, or $c_1 \ne 0, c_2 \ne 0$, a T-shaped or a cross-shaped crack develops. For a T-shaped crack, the SIDs also take maximum values at the debonding length. The values of the SIFs for a T-shaped crack were also obtained for bimaterial pairs Fe with Cu and Fe with Al.

Appendix

After deriving Eq. (18a), the function $\omega (\sigma )$ was used in the integrand of Eq. (17). However, if the function ${\left\{ {\omega (\sigma )+\overline{\omega (\sigma )} } \right\} }/2$ is used instead of $\omega (\sigma )$ [see Eq. (16)], the following result is derived:

$$\begin{aligned} H_1 (t_1 )= & {} \frac{\mu _2 \gamma _1 }{\kappa _2 +1}(\alpha _2^{*} \Delta T_2 -\alpha _1^{*} \Delta T_1 )\frac{\chi _1 (t_1 )}{2\pi i}\int \limits _M {\frac{\omega (\sigma )+\overline{\omega (\sigma )} }{\chi _1 (\sigma )(\sigma -t_1 )}\hbox {d}\sigma } \nonumber \\= & {} \frac{\mu _2 \gamma _1 }{\kappa _2 +1}(\alpha _2^{*} \Delta T_2 -\alpha _1^{*} \Delta T_1 )\frac{1}{1+\lambda _1 }\frac{\chi _1 (t_1 )}{2\pi i}\oint \limits _M {\frac{\omega (\sigma )+\overline{\omega (\sigma )} }{\chi _1 (\sigma )(\sigma -t_1 )}\hbox {d}\sigma } \nonumber \\= & {} \Lambda _1 \left[ {\begin{array}{l} 2\frac{E_0 }{1-t_1 }+2\frac{1-\lambda _1 }{2}\frac{E_0 \chi _1 (t_1 )}{\chi _1 (1)(1-t_1 )}+\sum \limits _{k=1}^N {\left\{ {1-\frac{\chi _j (t_j )}{\chi _j (\zeta _k )}} \right\} \frac{E_k }{\zeta _k -t_j }+E_c } \\ -\sum \limits _{k=1}^N {\left\{ {1-\frac{\chi _j (t_j )}{\chi _j ({\zeta }'_k )}} \right\} \frac{\overline{E_k } {\zeta }_k^{\prime 2} }{{\zeta }'_k -t_j }+\overline{E_c } +\sum \limits _{k=1}^N {\overline{E_k } {\zeta }'_k }} \\ \end{array}} \right] \end{aligned}$$

(43)

where the relation $E_0 =-\overline{E_0}$ has been used because $E_0$ is a pure imaginary number. $\Lambda _{1}$ is given by Eq. (18b). Equations (18) and (43) are identical because Eq. (16) holds.