1 Introduction

There are plenty of examples of mechanical systems, in dynamical properties and behaviour of which friction plays a crucial role. Friction can be a desired phenomenon or not, but in both cases, its appropriate and efficient mathematical modelling is a key part of analysis and synthesis of mechanical systems with frictional contacts. The classically understood friction model is a relation between a single component of the friction force and the one-dimensional relative displacement of the contacting bodies. This relation can have different levels of complexity, beginning with the classical Coulomb’s law of friction and ending with advanced relations, where additional state variables are often defined. These kinds of models can be directly applied in a mathematical description and analysis of dynamical systems with frictional contacts, where at each element of the contact, the same relative motion of the contacting surfaces occurs. However, in real life, one can encounter many examples of mechanical systems, where the above assumption cannot yield correct results. As examples, dynamics of rolling bearings, billiard balls, different kinds of tops, the wobblestone, polishing machine, disk clutches and many others can be given. Exact and correct results can always be obtained by detailed physical modelling and space discretisation in the vicinity of contact. Nonetheless, this approach leads to a computation cost increase and is inappropriate in fast numerical simulations. This is the reason of interest of many researchers in looking for simple approximate models of contact forces, which would be suitable for fast and realistic simulations of certain classes of mechanical systems with frictional contacts.

Contensou [1] has noticed that if the product of the normal component of relative angular velocity of the contacting bodies and the size of contact is sufficiently large, one should take the coupling between the friction force and moment into account. He has proposed an integral model of the resultant friction force under the assumption of fully developed sliding and Coulomb’s law of friction valid on each element of the circular contact. The results obtained by Contensou were then significantly developed by Zhuravlev [2], who presented an exact analytical solution to Contensou’s integral model and also proposed the corresponding approximant models based on the Padé expansions. Further developments and generalisations of the approximant models of the contact forces, including rolling resistance and assuming elliptical contact area, are proposed in the work [3]. An integral model of the friction force and moment was constructed under the assumption of classical Coulomb’s law and fully developed sliding over the planar contact zone of an arbitrary shape and general contact stress distribution. In the next step, a special model of contact distribution over the elliptic area was constructed, which can be understood as a kind of generalisation of Hertzian normal stress distribution, where a special distortion related to the rolling resistance was modelled. Certain original approximate models of the resultant friction force and moment, which are based on Padé approximants and their generalisations, have been presented in [3]. Special regularisations of these models, which enable to avoid singularities for vanishing relative motion as well as to take into account different values of static and kinetic friction coefficients, can be also found in [4, 5].

The topic of the present work is a part of the larger field concerning modelling and simulation of multibody systems with frictional contacts. The modelling methods dealing with those kinds of problems can be divided into two main branches, i.e. non-smooth models and regularised models [6]. In the regularised approaches, known also as penalty or complaint methods, the contact force is assumed as a continuous function of penetration of contacting bodies [7–9]. The frictional forces are then often formulated by the use of regularised Coulomb’s model of friction [10–13]. The regularisation can be a result of a need of simplification of the model but also very often corresponds to the physical nature of a real object (compliance of the bodies, microslips, etc.).

Stamm and Fidlin [14] have proposed a regularised two-dimensional model of friction forces appearing on a finite plane area based on elasto-visco-plastic theory, but requiring discretisation of the contact area. The authors have applied their model in modelling and analysis of a disk-on-a-disk system being, to a certain extent, a counterpart of a disk clutch, where alternating sliding and sticking solutions can occur [15]. The work [16] presents results of analytical studies of a similar system, where the approximations based on Taylor’s expansion of the friction force and moment for fully developed sliding are used.

In the present work, the authors apply their earlier developed models of the resultant friction force and moment in modelling and numerical simulations of the mechanical system being a certain modification of the disk-on-a-disk system analysed in the works [15, 16]. The present work is an extended version of the conference publication [17]. In comparison with the work [17], analysis of solution’s accuracy as a function of the “smoothing parameter” \(\varepsilon \) is included.

2 Modelling of friction forces

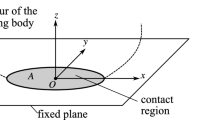
Let us consider a circular contact area of dimensionless form depicted in Fig. 1, where (i) the fully developed sliding; (ii) classical Coulomb’s law of friction valid on each element of the contact; (iii) constant friction coefficient; (iv) the fact that the relative motion of the contacting surfaces is a planar motion of rigid bodies is assumed. Aside from the aforementioned, also the following relations between real and dimensionless quantities describing the contact are assumed: \(\widehat{\mathbf{T}}_{s} =\mu \widehat{N}{} \mathbf{T}_{s}, \widehat{\mathbf{M}}_{s} =\mu \widehat{N}\widehat{a}{} \mathbf{M}_{s}, \widehat{\sigma }(x,y)=(\widehat{N}/\widehat{a}^{2})\sigma (x,y), \widehat{\mathbf{v}}_{{{\varvec{s}}}}=\widehat{a}{} \mathbf{v}_{s}\) and \(\widehat{{{\varvec{\upomega }}}}_{{{\varvec{s}}}} ={\varvec{\upomega }}_{s}\), where \(\widehat{\mathbf{T}}_{s}\) and \(\widehat{\mathbf{M}}_{s}\) are the real resultant friction force and moment of contact reduced to the centre A of contact \(F, \mathbf{T}_{s}\) and \(\mathbf{M}_{s}\)—the corresponding dimensionless resultant friction force and moment, \(\mu \)—friction coefficient, \(\widehat{N}\)—real normal loading of contact, \(\widehat{a}\)—characteristic dimension of contact (in this case, the real radius of the contact F), \(\widehat{\sigma }\) and \(\sigma \)—real and dimensionless contact pressures, \(\widehat{\mathbf{v}}_{{{\varvec{s}}}}\) and \(\mathbf{v}_{s}\)—relative real and dimensionless relative linear velocities at the point \(A, \widehat{{{\varvec{\upomega }}}}_{{{\varvec{s}}}} ={\varvec{\upomega }}_{s}\)—relative angular velocity in the plane of contact. Note that in all the introduced quantities, time is real.

Fig. 1
figure 1

Contact area

Full size image

Assuming that \(\mathbf{T}_{s} =-T_{sx} \mathbf{e}_{x} -T_{sy} \mathbf{e}_{y}\), \(\mathbf{M}_{s} =-M_{s} \mathbf{e}_{z}\), \(\mathbf{v}_{s} =v_{sx} \mathbf{e}_{x} +v_{sy} \mathbf{e}_y \) and \({{\varvec{\upomega }}}_{s} =\omega _{s} \mathbf{e}_z \), where \(\mathbf{e}_\xi \) is the unit vector along the axis \(\xi \), one can find the following integral expressions:

$$\begin{aligned} T_{sx}= & {} \iint \nolimits _{\mathrm{d}F} n(x,y) (v_{sx}-\omega _{s}y)\mathrm{d}x\mathrm{d}y,\nonumber \\ T_{sy}= & {} \iint \nolimits _{\mathrm{d}F} n(x,y)(v_{sy}+\omega _{s} x)\mathrm{d}x\mathrm{d}y,\nonumber \\ M_{s}= & {} \iint \nolimits _{\mathrm{d}F} n(x,y)\left( \omega _{s}(x^{2}+y^{2}) +v_{sy}x-v_{sx} y\right) \mathrm{d}x\mathrm{d}y, \end{aligned}$$
(1)

where

$$\begin{aligned} n(x,y)=\sigma (x,y)\left( \left( v_{sx}-\omega _{s}y\right) ^{2} +\left( v_{sy} +\omega _{s} x\right) ^{2}\right) ^{-1/2}. \end{aligned}$$

Since the model (1) requires integration over the contact area at each time step, it is not a suitable tool for fast and reliable numerical simulations. Based on the results presented in the previous works of the authors [3] and assuming a constant dimensionless contact pressure distribution on the circular contact area \(\sigma (x,y)=1/\pi \), one can derive the following two sets of the integral model (1) approximations

$$\begin{aligned} T_{sx}^{(I_{0,0})}= & {} \frac{v_{sx}}{\left( \left( v_{sx}^2 +v_{sy}^{2}\right) ^{\frac{m}{2}}+b^{m}\left| \omega _{s}\right| ^{m} \right) ^{\frac{1}{m}}},\nonumber \\ T_{sy}^{(I_{0,0})}= & {} \frac{v_{sy}}{\left( \left( v_{sx}^{2} +v_{sy}^{2}\right) ^{\frac{m}{2}}+b^{m} \left| \omega _{s}\right| ^{m}\right) ^{\frac{1}{m}}},\nonumber \\ M_{s}^{(I_{0,0})}= & {} \frac{\frac{2}{3}b\omega _{s}}{\left( \left( v_{sx}^{2}+v_{sy}^{2}\right) ^{\frac{m}{2}} +b^{m}\left| \omega _{s}\right| ^{m}\right) ^{\frac{1}{m}}}. \end{aligned}$$
(2)

and

$$\begin{aligned} T_{sx}^{(I_{1,1})}= & {} \frac{\left( v_{sx}^{2}+v_{sy}^{2} +b\omega _{s}^{2}\right) v_{sx}}{\left( \left( v_{sx}^{2}+v_{sy}^{2} \right) ^{\frac{3m}{2}}+b^{m}\left| \omega _{s}\right| ^{3m} \right) ^{\frac{1}{m}}},\nonumber \\ T_{sy}^{(I_{1,1})}= & {} \frac{\left( v_{sx}^{2}+v_{sy}^{2}+b\omega _{s}^{2} \right) v_{sy}}{\left( \left( v_{sx}^{2}+v_{sy}^{2}\right) ^{\frac{3m}{2}} +b^{m}\left| \omega _{s}\right| ^{3m}\right) ^{\frac{1}{m}}},\nonumber \\ M_{s}^{(I_{1,1})}= & {} \frac{\frac{2}{3}b\omega _{s}^{3} +\frac{1}{4}\omega _{s}\left( v_{sx}^{2}+v_{sy}^{2}\right) }{\left( \left( v_{sx}^{2}+v_{sy}^{2} \right) ^{\frac{3m}{2}}+b^{m}\left| \omega _{s}\right| ^{3m} \right) ^{\frac{1}{m}}}. \end{aligned}$$
(3)

The approximations (2–3), after the replacements \(v_{sx}=v_{s} \hbox {cos}\varphi _{s}\) and \(v_{sy}=v_{s}\hbox {sin}\varphi _{s}\), fulfil the following properties of the integral model (1)

$$\begin{aligned}&\left. {\frac{\partial ^{i}f^{\left( {I_{n1,n2} } \right) }}{\partial v_{s}^{i}}}\right| _{v_{s}=0}=\left. {\frac{\partial ^{i}f}{\partial v_{s}^i}}\right| _{v_{s} =0},\quad i=1,\ldots ,n_1,\nonumber \\&\left. {\frac{\partial ^{j}f^{\left( {I_{n1,n2}} \right) }}{\partial \omega _{s}^j}}\right| _{\omega _{s} =0} =\left. {\frac{\partial ^{j}f}{\partial \omega _{s}^j}}\right| _{\omega _{s} =0} , \quad j=1,\ldots ,n_{2}, \end{aligned}$$
(4)

where \(f=T_{sx}, T_{sy}, M_{s}\), while m and b are arbitrary constants. Note that the above approximations possess the same denominators, which, in general, is not necessary (see [3]), but allows for application of the later presented special form of regularisation.

In order to make comparison of the functions (1–3) simpler, one introduces the spherical coordinates

$$\begin{aligned} v_{sx}=\lambda _{s}\cos \theta _{s}\cos \varphi _{s}, \quad v_{sy} =\lambda _{s}\cos \theta _{s}\sin \varphi _{s}, \quad \omega _{s} =\lambda _{s}\sin \theta _{s}. \end{aligned}$$
(5)

The parameters m and b are optimised by searching for the best fitting of the corresponding functions on the representative (in the case of circularly symmetric contact pressure distribution) field \(\theta _{s}\in [0,{\uppi }/2]\) and \(\varphi _{s}=0\). For the functions (2), \(b=1.744\) and \(m=0.674\) are found, while for the approximations (3), one obtained \(b=0.765\) and \(m=0.452\). The corresponding plots are presented in Fig. 2. In the further modelling process, the approximations (3) will be used.

In the works [4, 5], a special kind of regularisation of the models of the types (2–3) has been proposed, allowing not only to avoid singularity for vanishing relative motion of the contacting surfaces, but also to model the situation in which the static friction coefficient is greater than the kinetic one. Applying that approach to the components (3), one gets

$$\begin{aligned} T_{sx\varepsilon }^{(I_{1,1})}= & {} \left( v_{sx}^{2} +v_{sy}^{2}+b\omega _{s}^{2}\right) v_{sx}\lambda _{sb\varepsilon },\nonumber \\ T_{sy\varepsilon }^{(I_{1,1})}= & {} \left( v_{sx}^{2} +v_{sy}^{2}+b\omega _{s}^{2}\right) v_{sy}\lambda _{sb\varepsilon },\nonumber \\ M_{s\varepsilon }^{(I_{1,1})}= & {} \left( \frac{2}{3}b\omega _{s}^{3} +\frac{1}{4}\omega _{s}\left( v_{sx}^{2} +v_{sy}^{2}\right) \right) \lambda _{sb\varepsilon }, \end{aligned}$$
(6)

where

$$\begin{aligned} \lambda _{sb\varepsilon } =\frac{1}{\sqrt{\left( {\left( {v_{sx}^{2} +v_{sy}^2}\right) ^{\frac{3m}{2}}+b^{m}\left| {\omega _{s}} \right| ^{3m}}\right) ^{\frac{2}{m}}+\varepsilon ^{6}}}+ \eta ^{{\prime }}\left( \eta \right) \frac{\varepsilon ^{9}}{\left( {\left( {\left( {v_{sx}^2 +v_{sy}^2} \right) ^{\frac{3m}{2}}+b^{m}\left| {\omega _{s}}\right| ^{3m}} \right) ^{\frac{2}{m}}+\varepsilon ^{6}} \right) ^{2}}, \end{aligned}$$

and where \(\varepsilon \) is a small numerical parameter. The coefficient \({\eta }'\) is a function of the parameter \(\eta \) equal to the maximum magnitude of the resultant dimensionless friction force (or \(\eta =\mu _{0}/\mu \), where \(\mu _{0}\) is the static friction coefficient). This function can be approximated as \(\eta ^{\prime }\left( \eta \right) \approx -13.607+30.893\eta -22.01\eta ^{2}+5.878\eta ^{3}\) for \(\eta \in [1,1.3]\) and \(\eta ^{\prime }(\eta )\approx -2.41+3.985\eta -0.3581\eta ^{2}+0.0493\eta ^{3}\) for \(\eta \in [1.3,2.7]\), with the error \(\left| \Delta \eta \right| <0.001\) (see [5]). Figure 3 presents exemplary plots of the model (6) near-zero relative motion, for \(\theta _{s}=\pi /4, \varphi _{s}=0\), \(\eta =2\) and \(\varepsilon =10^{-3}\).

Fig. 2
figure 2

Comparison of the approximate components \(T_{sx}^{(I_{0,0})}\) (a), \(M_{s}^{(I_{0,0})} \) (b), \(T_{sx}^{(I_{1,1})} \) (c), \(M_{s}^{(I_{1,1})}\) (d) of the friction model (grey curves) with the corresponding full integral components \(T_{sx}\) and \(M_{s}\) (black curves), for \(\varphi _{s}=0\)

Full size image
Fig. 3
figure 3

Approximations \(T_{sx\varepsilon }^{(I_{1,1})}\) (a), \(M_{s\varepsilon }^{(I_{1,1})} \) (b) near-zero relative motion—for \(\theta _{s} =\pi /4\), \(\varphi _{s}=0\), \(\eta ^{\prime }(2)=4.479\) and \(\varepsilon =10^{-3}\)

Full size image

3 Mathematical model of the pendulum

In Fig. 4, a physical conception of the special mechanical system, being a certain modification of the disk-on-a-disk system analysed in the works [7, 8], is presented. A physical pendulum of a mass M and a moment of inertia B with respect to the mass centre C is rotationally connected with the use of the joint A to a light platform. The platform is mounted on the support with the use of elasto-damping elements in such a way that it cannot rotate. The origin O of the introduced coordinate system OXY is defined as a position of the point A of the pendulum in its equilibrium position in the case of no friction forces acting on the mechanical system. The pendulum is equipped with a flat disk of a radius R centred in the point A. The disk is in contact with a larger rotating rigid body performing pure rotational motion with angular velocity \(\omega _{0}\) about the centre S. A constant contact pressure distribution and Coulomb’s law of friction on each element of the circular contact between the bodies are assumed.

Fig. 4
figure 4

Physical concept of the mechanical system

Full size image

The governing equations of the presented mechanical system read

$$\begin{aligned}&M\ddot{X}_{C}+ k_{X}\left( X_{C}-e\cos \varphi \right) + c_{X}\left( \dot{X}_{C}+e \dot{\varphi }\sin \varphi \right) +\mu \widehat{N}T_{{sx\varepsilon }}^{{\left( I_{{1,1}}\right) }}=0,\nonumber \\&M\ddot{Y}_{C}+k_{Y}\left( Y_{C}-e\sin \varphi \right) + c_{Y}\left( \dot{Y}_{C}-e \dot{\varphi }\cos \varphi \right) + \mu \widehat{N}T_{{sy\varepsilon }}^{{\left( I_{{1,1}}\right) }}= 0\nonumber \\&B\ddot{\varphi }+e\left( Mg+k_{X}\left( X_{C}-e\cos \varphi \right) +c_{X}\left( \dot{X}_{C}+e~\dot{\varphi }\sin \varphi \right) +\mu \widehat{N}T_{{sx\varepsilon }}^{{\left( {I_{{1,1}}} \right) }}\right) \sin \varphi +\nonumber \\&\quad -e\left( k_{Y}\left( Y_{C}-e\sin \varphi \right) +c_{Y} \left( {\dot{Y}_{C}-e~\dot{\varphi }\cos \varphi }\right) +\mu \widehat{N}T_{{sy\varepsilon }}^{{\left( {I_{{1,1}}} \right) }}\right) \cos \varphi + c_{\varphi }\dot{\varphi }+\mu \widehat{N} RM_{{s\varepsilon }}^{{\left( {I_{{1,1}}} \right) }}=0 \end{aligned}$$
(7)

where \(X_C\) and \(Y_C\) are the coordinates of the mass centre C; \(\varphi \)—angular position of the pendulum; \(e=AC\)—distance between the point A and the mass centre \(C; k_X\) and \(k_Y\)—stiffness coefficients of the elements supporting the rotational joint A; \(c_X \) and \(c_Y \)—the corresponding damping coefficients; \(c_\varphi \)—the coefficient of damping in the rotational joint A; \(\mu \)—kinetic friction coefficient; \(\widehat{N}\)—normal loading of contact; \(X_S \) and \(Y_S \)—coordinates of the point S; g—gravitational acceleration. As a model of the resultant friction force and moment, the relations (6) are applied.

The kinematic arguments of the functions (6) read

$$\begin{aligned} \omega _{s}= & {} \dot{\varphi }-\omega _{0},\nonumber \\ v_{{sx}}= & {} \frac{{\dot{X}_{C} +e~\dot{\varphi }\sin \varphi + \omega _{0}\left( Y_{C} -e\sin \varphi -Y_{S}\right) }}{R},\nonumber \\ v_{{sy}}= & {} \frac{{\dot{Y}_{C}-e~\dot{\varphi }\cos \varphi - \omega _{0}\left( X_{C}-e\cos \varphi -X_{S}\right) }}{R}. \end{aligned}$$
(8)

In some of the figures, we present motion of the point A, the coordinates of which read

$$\begin{aligned} X_A= & {} X_{C}-e\cos \varphi ,\nonumber \\ Y_A= & {} Y_C -e\sin \varphi . \end{aligned}$$
(9)

4 Numerical simulations

In all the numerical simulations presented in this section, the following parameters are fixed: \(g=9.81\hbox {m}/\hbox {s}^{2}\), \(b=0.452, m=0.765\) and \(\varepsilon =10^{-3}\).

In Fig. 5a, a bifurcation diagram of the system exhibited in Fig. 4, with constant angular velocity \(\omega _{0}\) playing a role of a bifurcational parameter, is presented. The remaining system parameters read: \(M=1.2\,\hbox {kg}\), \(B=0.01\,\hbox {kg}\,\hbox {m}^{2}\), \(e=0.1\,\hbox {m}\), \(k_X =k_{Y}=1000\,\hbox {N}/\hbox {m},c_{X}=c_{Y} =0.1\,\hbox {N}\,\hbox {s}/\hbox {m},c_{\varphi } =0.1\,\hbox {N}\,\hbox {m}\,\hbox {s}, X_{s} =0\,\hbox {m}, Y_{s} =0\,\hbox {m},R=0.02\,\hbox {m}, \widehat{N}=25\,\hbox {N}, \mu =1\) and \(\eta =1\) (the static friction coefficient is equal to the kinetic one). For low angular velocities, one observes a stable equilibrium position—see Fig. 6a, where for \(\omega _{0} =30\frac{\hbox {rad}}{\hbox {s}}\), the corresponding time history of the angle \(\varphi \) is presented. For greater values of \(\omega _{0}\), a stable periodic attractor appears—see Fig. 6b. A further increase in \(\omega _{0} \) leads to rich bifurcational and irregular dynamics with full rotations of the pendulum—see Fig. 7. Figure 5b exhibits another example of a bifurcation diagram, where the following system’s parameters are changed: \(e=0.025\,\hbox {m}\), \(k_X =k_Y =2000\,\hbox {N}/\hbox {m},\,\widehat{N}=25\,\hbox {N}\). In this case, the system dynamics is drastically different. For example, one cannot observe stable periodic solutions for low angular speeds of the disk. Instead of this, there is a sudden jump from stable equilibrium to a chaotic region.

Fig. 5
figure 5

Two examples of a bifurcation diagram with angular frequency \(\omega _{0} \) as a control parameter

Full size image
Fig. 6
figure 6

Examples of system behaviour corresponding to the bifurcation diagram presented in Fig. 5, for \(\omega _{0} =30\,\hbox {rad}/\hbox {s}\) (a), \(\omega _{0} =40\,\hbox {rad}/\hbox {s}\) (b)

Full size image
Fig. 7
figure 7

Trajectory of the system (a, b) and Poincaré section (c, d) corresponding to the bifurcation diagram presented in Fig. 5 for \(\omega _{0}=61.5\,\hbox {rad}/\hbox {s}\)

Full size image

Figure 8 presents examples of periodic stick–slip oscillations of the investigated mechanical system, where the following parameters are assumed: \(M=1.2\,\hbox {kg}\), \(B=0.01\,\hbox {kg}\,\hbox {m}^{2}\), \(e=0.1\,\hbox {m}\), \(k_X =k_Y=100\,\hbox {N}/\hbox {m}, c_X =c_Y =0.1\,\hbox {N}\,\hbox {s}/\hbox {m},\, c_\varphi =0.1\,\hbox {N}\,\hbox {m}\,\hbox {s},\, X_{s} =0\,\hbox {m}\), \(\omega _{0} =0.6\,\hbox {rad}/\hbox {s}, R=0.1\,\hbox {m}\), \(N=6\,\hbox {N}\), \(\mu =1\) and \(\eta =2.5\). The position of the joint S along the axis X is different for each of the presented solutions: \(Y_{s} =-0.1\,\hbox {m}\) (a, b), \(Y_{s} =0\,\hbox {m}\) (c, d), \(Y_{s} =0.1\,\hbox {m}\) (e, f).

Fig. 8
figure 8

Examples of stick–slip oscillations for \(Y_{s} =-0.1\,\hbox {m}\) (a, b), \(Y_{s} =0\,\hbox {m}\) (c, d), \(Y_{s}=0.1\,\hbox {m}\) (e, f)

Full size image
Fig. 9
figure 9

Stick–slip solution computed with \(\varepsilon =10^{-4}\) (a) and the difference between the same solution obtained with \(\varepsilon =10^{-3}\) (b), \(10^{-3}\), (c), \(10^{-1}\) (d) and the solution for \(\varepsilon =10^{-4}\) treated as a pattern

Full size image

In Fig. 9, the results of analysis of solution’s accuracy as a function of the parameter \(\varepsilon \) are depicted. In order to make two solutions comparable in the time domain, one introduced the synchronising element, i.e. periodically varying angular velocity of the driving disk \(\omega _{0} (t)=\hbox {cos}\left( {1\frac{\hbox {rad}}{\hbox {s}}t}\right) \frac{\hbox {rad}}{\hbox {s}}\). Other parameters are the same as in the case of analysis presented in Fig. 8. The corresponding stick–slip solution, obtained for \(\varepsilon =10^{-4}\), is presented in Fig. 8a. Then, the difference between the same solution obtained with \(\varepsilon =10^{-3}\) (b), \(10^{-3}\), (c), \(10^{-1}\) (d) and the solution for \(\varepsilon =10^{-4}\) treated as a pattern is shown in the remaining subplots of Fig. 9.

For all the numerical computations presented in this study, Wolfram Mathematica 10.3 package has been used. For numerical solution to the differential equations, the method NDSolve with the default settings has been implemented.

5 Conclusions

In the present work, examples of models of the resultant friction force and moment based on previous works of the authors have been presented. They are simple functions, which can be an effective substitute for the exact integral model, suitable for fast and realistic computer simulations of a certain class of mechanical systems with frictional contacts.

These models, in their primary form, concern the case of a fully developed sliding on the contact area and possess singularity for the case of lack of the relative motion. The applied regularisation occurred to be an effective method to avoid that problem and take into account different values of static and kinetic friction coefficients. The drawbacks include stiff differential equations and the change in physical properties of the system near the stick mode.

In order to test the developed models of friction forces, a mathematical model of a special mechanical system is built, which is some modification of the disk-on-a-disk system analysed in the works [15, 16], being a strongly simplified disk clutch. It is expected that the proposed model can exhibit much richer bifurcational dynamics, allowing for testing different aspects of friction models. It should be noted that the presented work is in progress, and only preliminary results are reported. Future construction of the corresponding experimental rig is also considered.

One has to pay his attention to the problem of accuracy of approximation (3). Since there is a difference between this approximation and original integral model (1) seen in Fig. 2, one has to expect the corresponding difference between the bifurcation dynamics (observed in Fig. 5) of the pendulum with the friction force and moment described by these two models. Since numerical simulations with the full integral model (1) are very inconvenient and time-consuming, we do not present this comparison on bifurcation diagrams. On the other hand, one has to bear in mind that the main goal of modelling and numerical simulations is to predict and explain dynamics of real objects. Since both the integral friction model and its approximation can describe the real friction phenomenon most approximately, the differences between the models (1) and (3) become less important. Their usefulness can be eventually validated by experiments. Note that a more general class of these models was successfully verified during experimental investigations of the wobblestone dynamics [18].