A nonlocal constitutive model generated by matrix functions for polyatomic periodic linear chains

Abstract

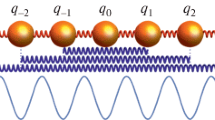
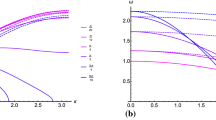
We establish a discrete lattice dynamics model and its continuum limits for nonlocal constitutive behavior of polyatomic cyclically closed linear chains being formed by periodically repeated unit cells (molecules), each consisting of ${n \geq 1}$ atoms which all are of different species, e.g., distinguished by their masses. Nonlocality is introduced by elastic potentials which are quadratic forms of finite differences of orders ${m \in \mathbf{N}}$ of the displacement field leading by application of Hamilton’s variational principle to nondiagonal and hence nonlocal Laplacian matrices. These Laplacian matrices are obtained as matrix power functions of even orders 2m of the local discrete Laplacian of the next neighbor Born-von-Karman linear chain. The present paper is a generalization of a recent model that we proposed for the monoatomic chain. We analyze the vibrational dispersion relation and continuum limits of our nonlocal approach. “Anomalous” dispersion relation characteristics due to strong nonlocality which cannot be captured by classical lattice models is found and discussed. The requirement of finiteness of the elastic energies and total masses in the continuum limits requires a certain scaling behavior of the material constants. In this way, we deduce rigorously the continuum limit kernels of the Laplacian matrices of our nonlocal lattice model. The approach guarantees that these kernels correspond to physically admissible, elastically stable chains. The present approach has the potential to be extended to 2D and 3D lattices.