Instabilities of a thin viscoelastic liquid film flowing down an inclined plane in the presence of a uniform electromagnetic field

Abstract

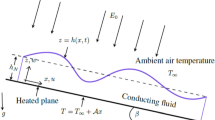
The effect of a uniform electromagnetic field on the stability of a thin layer of an electrically conducting viscoelastic liquid flowing down on a nonconducting inclined plane is studied under the induction-free approximation. Long-wave expansion method is used to obtain the surface evolution equation. The stabilizing role of the magnetic parameter M and the destabilizing role of the viscoelastic parameter Γ as well as the electric parameter E on this flow field are established. A novel result which emerges from our analysis is that the stabilizing effect of M holds no longer true for both viscous and viscoelastic fluids in the presence of electromagnetic field. It is found that when E exceeds a certain critical value depending on Γ, magnetic field exhibits the destabilizing effect on this flow field. Indeed, this critical value decreases with the increase of the viscoelastic parameter Γ since it has a destabilizing effect inherently. Another noteworthy result which arises from the weakly nonlinear stability analysis is that both the subcritical unstable and supercritical stable zones are possible together with the unconditional stable and explosive zones for different values of Γ depending on the wave number k.

Appendices

Appendix: A

$$\begin{array}{@{}rcl@{}} L_0 &\equiv& \frac{\partial}{\partial t} + A \frac{\partial}{\partial x} + \left( B\frac{\partial^2}{\partial x^2} + C \frac{\partial^4}{\partial x^4} \right), \end{array} $$

(72)

$$\begin{array}{@{}rcl@{}} L_1 &\equiv& \frac{\partial}{\partial t_1}+\frac{\partial}{\partial x_1} \left[A + 2 \left( B \frac{\partial}{\partial x } + 2 C \frac{\partial^3} {\partial x^3 } \right) \right], \end{array} $$

(73)

$$\begin{array}{@{}rcl@{}} L_2 &\equiv& \frac{\partial}{\partial t_2} + \frac{\partial^2} {\partial x_1^2} \left( B + 6 C \frac{\partial^2}{\partial x^2} \right), \end{array} $$

(74)

$$\begin{array}{@{}rcl@{}} N_2 &=& A^{\prime} \eta_1 \frac{\partial \eta_1}{\partial x} + B^{\prime} \eta_1 \frac{\partial^2 \eta_1}{\partial x^2} + C^{\prime} \eta_1 \frac{\partial^4 \eta_1}{\partial x^4}, \end{array} $$

(75)

$$\begin{array}{@{}rcl@{}} N_3 &=& A^{\prime} \left[\eta_1 \left( \frac{\partial \eta_2}{\partial x} + \frac{\partial \eta_1}{\partial x_1}\right) + \eta_2\frac{\partial \eta_1}{\partial x} \right]\\ &&+ B^{\prime} \left[ \eta_1 \left( \frac{\partial^2 \eta_2}{\partial x^2} + 2 \frac{\partial^2 \eta_1}{\partial x \partial x_1}\right) + \eta_2 \frac{\partial^2 \eta_1} {\partial x^2} \right]\\ &&+ C^{\prime} \left[\eta_1 \left( \frac{\partial^4 \eta_2}{\partial x^4} + 4 \frac{\partial^4 \eta_1}{\partial x^3 \partial x_1} \right) + \eta_2 \frac{\partial^4 \eta_1}{\partial x^4} \right]\\ &&+ \frac{1}{2} A^{\prime\prime}{\eta_1}^2 \frac{\partial \eta_1}{\partial x}\,+\, \frac{1}{2} B^{\prime\prime}{\eta_1}^2 \frac{\partial^2 \eta_1}{\partial x^2} + \frac{1}{2} C^{\prime\prime}{\eta_1}^2 \frac{\partial^4 \eta_1}{\partial x^4}. \end{array} $$

(76)

Appendix: B

$$\begin{array}{@{}rcl@{}} \omega_i^{\prime} &=& \omega_i \sigma^{-2}, \end{array} $$

(77)

$$\begin{array}{@{}rcl@{}} J_0 &=& J_{0r} + i J_{0i} = 0 + i 2k \left( 2 C k^2 - B \right)\sigma^{-1}, \end{array} $$

(78)

$$\begin{array}{@{}rcl@{}} J_1 &=& J_{1r} + i J_{1i} = \left( B - 6 C k^2 \right) + i 0, \end{array} $$

(79)

$$\begin{array}{@{}rcl@{}} J_2 &=& - A^{\prime} {\bar H_{1i}}\\ &&+ \left[ \frac{1}{2} \left( C^{\prime\prime} k^4 - B^{\prime\prime} k^2 \right) + \left( 7 C^{\prime} k^4 - B^{\prime} k^2 \right) {\bar H_{1r}} \right], \\ &=& \frac{1}{2} \left( -B^{\prime\prime} k^2 + C^{\prime\prime} k^4 \right)\\ &&+ \left[ \frac{(A^{\prime})^2 k^2 \,-\, 2 \left( B^{\prime} k^2 \,-\,7 C^{\prime} k^4 \right) \left( B^{\prime} k^2 \,-\, C^{\prime} k^4 \right)} {16 C k^4 \,-\, 4 B k^2} \right], \end{array} $$

(80)

$$\begin{array}{@{}rcl@{}} J_4 &=& A^{\prime} k {\bar H_{1r}} + \frac{1}{2} A^{\prime\prime} k + \left( 7 C^{\prime} k^4 - B^{\prime} k^2 \right) {\bar H_{1i}}, \\ &=& \frac{1}{2}A^{\prime\prime} k\\ &&+ \left[ \frac{A^{\prime} k \left( B^{\prime} k^2 \,-\,7 C^{\prime} k^4 \right) \,+\, 2 A^{\prime} k \left( B^{\prime} k^2 \,-\, C^{\prime} k^4 \right)} {16 C k^4 - 4 B k^2} \right]. \end{array} $$

(81)