1 Introduction

The high northern latitudes have experienced strong climate variations during the last decades (McBean et al. 2005). Some polar regions exhibit, for example, a warming of as much as 2°C per decade (Rigor et al. 2000). This was accompanied by a record minimum in ice extent in summer 2007, which was only 4.28 × 106 km2 and thus about 50% lower than the conditions in the 1950s and 1970s (Stroeve et al. 2008). Climate change projections, such as those discussed in the International Panel of Climate Change (IPCC) Fourth Assessment Report (AR4) indicate that the already ongoing warming due to enhanced anthropogenic CO2 emissions is most pronounced over the continents and over the high latitudes (Meehl et al. 2007). On the other hand, large decadal to multidecadal variations have also been reported from the Arctic that are likely unrelated to external forcing (Overpeck et al. 1997; Polyakov and Johnson 2000; Schmith and Hansen 2003). Long-term variations of surface air temperature (SAT) are largest in the high northern latitudes (Johannessen et al. 2004; Kuzmina et al. 2008) with a pronounced warming in the 1930s and 1940s similar in magnitude to the late 20th/early 21st century. To discriminate between anthropogenically forced global warming and natural variability of the atmosphere-ocean-sea ice system it is therefore necessary to improve our understanding of the processes involved in the latter.

Various mechanisms have been proposed to explain the strong variations in the Arctic SAT record and a review was recently given by Goosse and Holland (2005). Most prominent are studies that relate the observed Arctic warming to recent trends in the North Atlantic Oscillation (NAO) or Arctic Oscillation (AO) (e.g. Dickson et al. 2000). More recently, analyzes have been extended to higher order empirical orthogonal functions (EOF) of the atmospheric circulation. Quadrelli and Wallace (2004) state that much of the Northern Hemisphere climate variations can be represented in terms of the two leading EOFs of sea level pressure (SLP) and Overland and Wang (2005) describe the Arctic climate variations for the second half of the 20th century by a phase space trajectory based on the two leading EOFs. Other studies emphasize the role of the Atlantic meridonal overturning circulation (AMOC). AMOC variations are related to pronounced changes in meridional heat transport and thus may influence Arctic climate (e.g. Polyakov and Johnson 2000). However, since observational data are scarce, this is mainly based on results from coupled ocean-atmosphere models (Delworth et al. 1993, 1997; Jungclaus et al. 2005). Ikeda et al. (2001), Bengtsson et al. (2004), and Goosse and Holland (2005) showed that increased heat transport into the Barents Sea affects the local interactions between atmosphere and ocean. The associated warming in the Barents Sea reduces the SLP that feed back positively on ocean circulation and heat transport. In summary, meridional heat transfer variations into the Arctic either through large-scale atmospheric or ocean circulation changes or through (locally) coupled processes play the dominant role. This is particularly evident during polar night, when the lateral fluxes determine surface air temperature fluctuation almost entirely.

Two recent publications, Shaffrey and Sutton (2006) and van der Swaluw et al. (2007) analyzed the decadal-scale variations in ocean and atmosphere heat transport using data from long control integrations with the HadCM3 climate model. They find that both components are anticorrelated between 30 and 80°N and that this anticorrelation is strongest around 70°N. Not only are the heat transports anticorrelated, their anomalies are also of the same size and the authors name the process “Bjerknes Compensation” (BC) referring to Bjerknes (1964). The mechanism behind the BC is given as follows: positive oceanic heat transport anomalies (related, for example to AMOC variations) causes enhanced warming and sea ice melt in high northern latitudes. The absence of sea ice leads to drastic ocean-to-atmosphere heat flux changes warming the overlying air. The reduced meridional temperature gradient in the atmosphere leads to reduced baroclinicity and reduced (eddy) heat transport (van der Swaluw et al. 2007).

Given the sensitivity of the high-latitude climate to changes in meridional heat transport, we wish to analyze the role of the BC mechanism in shaping the Arctic climate. If the heat transport compensation were complete, then this mechanism would tend to smooth Arctic-wide climate variations due to lateral changes, since variations in one component would be compensated by the other. Furthermore, BC, as a negative feedback, would act against positive feedbacks, such as those invoked to explain the 1930s to 1940s warming in the Arctic. Here we analyze the mechanisms of ocean and atmospheric heat transport variation in detail, demonstrate their regional impacts, and relate them to decadal to multidecadal Arctic climate variations.

2 Model and experiment description

The numerical experiment analyzed here is the control integration carried out for the IPCC AR4 using the Max-Planck-Institute for Meteorology global atmosphere—ocean—sea ice model ECHAM5/MPIOM (European Centre for medium weather forecast—HAMburg/Max-Planck-Institute Ocean Model). The atmosphere model ECHAM5 (Roeckner et al. 2003) is run at T63 resolution, which corresponds to a horizontal resolution of about 1.875° × 1.875°. It has 31 vertical levels up to 10 hPa. The ocean model MPI-OM (Marsland et al. 2003) includes a Hibler-type dynamic-thermodynamic sea ice model with viscous-plastic rheology (Hibler 1979). The ocean grid is an Arakawa C-grid and allows for an arbitrary placement of the grid poles. In this setup, the model’s North and South Pole are shifted to Greenland and to the center of Antarctica (c.f., Jungclaus et al. 2006a, Fig. 1) and the grid spacing varies between about 15 km around Greenland and 184 km in the tropical Pacific. In the vertical, there are 40 unevenly spaced levels. The simulated mean climate and variability characteristics of the pre-industrial IPCC AR4 control experiment analyzed here are similar to the simulation under present-day greenhouse gas forcing discussed in Jungclaus et al. (2006a). A number of studies (e.g., Bengtsson et al. 2006; Jungclaus et al. 2006b) have evaluated the ECHAM5/MPIOM IPCC AR4 20th century and scenario integrations and Koenigk et al. (2007) investigated future Arctic freshwater exports. In the present paper, 505 years of the IPCC AR4 pre-industrial experiment are used to study decadal-scale variations in the Arctic whereas Koenigk et al. (2008) focused on the interannual variability of sea ice in the Barents Sea. According to the latter, sea ice conditions in the Arctic are relatively well simulated compared to satellite observations by Johannessen et al. (2002).

Fig. 1
figure 1

Map of the Arctic domain

Full size image

The calculation of the global heat transport through the atmosphere and the oceans follows Shaffrey and Sutton (2006) and van der Swaluw et al. (2007). The (implied) meridional atmospheric heat transport HTRA is derived by integrating the sum of the divergence of the zonally integrated surface heat flux F sfc and the energy flux coming in as radiation at the top of the atmosphere F toa. The global ocean heat transport HTRO is obtained by integrating the divergence of the zonally integrated surface flux from the atmosphere into the ocean F sfc minus the time derivative of the ocean heat content (OHC):

$$ \frac{\partial HTRO}{\partial y} = - \frac{\partial OHC}{\partial t} - F_{\text{sfc}} ,\quad \frac{\partial HTRA}{\partial y} = F_{\text{sfc}} - F_{\text{toa}} , $$
(1)

or, using the dependence on the surface flux field in both equations:

$$ \frac{\partial HTRO}{\partial y} = - \frac{\partial HTRA}{\partial y} - \frac{\partial OHC}{\partial t} - F_{\text{toa}} $$
(2)

from which it follows that BC requires that the second and third term on the right hand side are both small. For these implied heat transports, monthly mean model output was used. In addition to the atmospheric heat transport derived from the monthly flux fields, the advective total energy transport at 70°N was directly calculated from six-hourly atmosphere model output, following Semmler et al. (2005) and Keith (1995).

$$ HTRA^{\prime} = \iint {(c_{p} T + gz + Lq_{v} )v\frac{dp}{g}}dx $$
(3)

Here c p is the specific heat of dry air, T is temperature, L is latent heat of condensation, q v the water vapor content, g acceleration due to gravity, z geopotential height, v is wind velocity, and p is pressure. We refer to the sum of all three terms as total (moist static) energy and to the sum of the first and second term as dry static energy. Since HTRA′ is based on the calculation of the energy transport in every grid box along the latitude circle, information on the spatial structure of the atmospheric energy transport become available. At 70°N, there are slight differences between HTRA and HTRA′, probably due to the effects of diffusive heat transports and changes in the atmospheric heat storage. However, the decadal-scale variability is almost identical (see below).

In general, we apply an 11-year running mean to smooth the data throughout this paper to emphasize decadal time scales. Smoothing the data on the decadal time scale might increase the correlation coefficients but reduces the degrees of freedom. The statistical significance of the computed correlations and regressions are estimated using a t test taking serial correlations into account by using the lagged autocorrelations of the respective time series to calculate an effective number of observations n eff

$$ n_{\text{eff}} = {n \mathord{\left/ {\vphantom {n {\left[ {1 + 2\left( {r_{1} r^{\prime}_{1} + r_{2} r^{\prime}_{2} + \ldots + r_{n} r^{\prime}_{n} } \right)} \right],}}} \right. \kern-\nulldelimiterspace} {\left[ {1 + 2\left( {r_{1} r^{\prime}_{1} + r_{2} r^{\prime}_{2} + \ldots + r_{n} r^{\prime}_{n} } \right)} \right],}} $$
(4)

where n is the original sample size and r 1 and \( r^{\prime}_{1} \) are the lag-1 autocorellations of the two time series, r 2, \( r^{\prime}_{2} \) are the corresponding lag-2 autocorrelations etc. (Von Storch and Zwiers 1999; Sorteberg and Kvingedal 2006). Typical decorrelation times for the time series under consideration here are 6–7 years and a typical bound of significant correlation is about 0.35.

3 Results

3.1 Decadal-scale heat transport variations and ocean-atmosphere interaction

3.1.1 Mean oceanic and atmospheric heat and energy transports

The long-term averaged ocean heat transport in the IPCC AR4 pre-industrial control experiment is similar to the one in the present-day control integration discussed in Jungclaus et al. (2006a, c.f. their Fig. 7). The maximum Atlantic heat transport in the simulation discussed here is 1.15 PW (1 PW = 1015 W) around 20°N and 0.28 PW at 70°N. Based on a synoptic section from Greenland to Norway across the Greenland Sea (approximately at 70°N), Oliver and Heywood (2003) applied an inverse method and estimated a total heat transport of 0.20 ± 0.08 PW. The simulated mean global atmospheric heat transport as a function of latitude (not shown) exhibits the typical symmetric shape (e.g., Trenberth and Solomon 1994) with maxima of poleward heat transport exceeding 5 PW at 41°N and 40°S, respectively. While the oceanic heat transport into the Arctic is almost entirely confined to the Atlantic sector (Fig. 1), the zonal structure of the atmospheric energy fluxes are determined by the large scale atmospheric circulation and its proper representation in the model. At 70°N, the northward atmospheric energy transport is 1.55 PW. Longitudinal variations of the vertically integrated meridional energy flux displayed as a function of calendar months indicate that there is a banded structure of northward and southward fluxes (Fig. 2). Both magnitude and structure are very similar to the respective ones analyzed by Serreze et al. (2007) based on the European Center for Medium Range Weather Forecast ERA40 data and our Fig. 2 can directly be compared with their Fig. 6a. The location of the inflow and outflow minima and maxima, respectively, as well as their seasonal variations are well represented in our control integration. The main difference is that the model result discussed here has a somewhat smoother spatial structure, most likely due to the lower resolution (T63 vs. T159). The most prominent region of northward flow is centered around 50°W, east of the axis of the mean 500 hPa eastern North American trough pointing to contributions from the time mean flow and eddy transport associated with the North American storm track (note that the vertical structure of the mean northward flow is tilted towards the west with height so that an inspection of the surface pressure field may be misleading (Overland and Turet 1994, their Fig. 8). Pronounced equatorward flow is seen to the west, centered around 110°W associated with the descending leg of the 500 hPa North American ridge. A broad region of seasonal varying poleward flow characterizes the Eurasian sector (120°E to 180°) whereas there is mean equatorward flow in the sector 20°–90°E. The major pathways of energy flux by the transient eddy field are through the Greenland Sea sector and the vicinity of Bering Strait in the Pacific (c.f., Overland and Turet 1994, their Fig. 9).

Fig. 2
figure 2

Atmospheric energy transport at 70°N as a function of longitude and calendar month derived from the 505-year pre-industrial control experiment. Units are 109 W m−1. Positive values indicate northward transport

Full size image

3.1.2 Decadal scale heat transport variations and ocean atmosphere interaction

The correlations of decadal-scale oceanic and atmospheric heat transports calculated for each latitude (Fig. 3) are negative in the Northern Hemisphere except for the very high latitudes. Similar to the HadCM3 results discussed by Shaffrey and Sutton (2006), the anticorrelation is strongest near 70°N indicating a pronounced interaction between ocean and atmosphere also in ECHAM5/MPIOM. In our model the correlation between the oceanic heat transport near 70°N (HTRO70) and the atmospheric heat transport at the same latitude (HTRA70) is -0.62 (Fig. 3) whereas it is −0.84 in HadCM3 (Van der Swaluw et al. 2007, cf., their Fig. 1). In accordance with Van der Swaluw et al. (2007), the strongest anticorrelation is found when the ocean is leading the atmosphere by 1–2 years, indicating a driving role of the ocean. Also in ECHAM5/MPIOM, the correlation is much stronger for the decadally-smoothed data compared to the annual data (not shown). The time series of the HTRO70 and HTRA70 anomalies (Fig. 4a) exhibit decadal standard deviations of about 0.01 PW. The heat transport anomalies are characterized by decadal variations reaching up to 0.03 PW. Heat transport variations of the order of 0.01–0.03 PW appear to be quite small in comparison with the 1.55 PW mean that the atmosphere provides at 70°N. However, if one divides the anomalous energy surplus by the area north of 70°N to translate the boundary transports into a representative heat flux (e.g., Semmler et al. 2005; Serreze et al. 2007), one arrives at a considerable forcing of about 1 to 3 W m−2.

Fig. 3
figure 3

Correlation between the oceanic and atmospheric meridional heat transports as a function of lead/lag time and latitude. At positive lags the ocean is leading. The gray-shaded areas indicate regions where the significance exceeds 95% according to a t test

Full size image
Fig. 4
figure 4

Time series of quantities representing oceanic and atmospheric heat transports at 70°N: a implied atmosphere (black) and ocean (red) heat transport anomalies calculated from Eq. (1); the blue line is the sum of all three terms from the right-hand-side of Eq. (2). b Terms representing (green) the time derivative of the ocean heat content and (red) the TOA radiation; the blue line is the sum of the green and the red curve. c Atmospheric heat transport calculated from Eq. (1) (black) together with the advective energy transport calculated from Eq. (3): (blue) dry-static energy only and (red) total energy. All annual fields have been smoothed using an 11-year running mean

Full size image

Overall, HTRO70 and HTRA70 anomalies tend to be of opposite sign and similar magnitude (Fig. 4a), but the compensation is not always perfect. In fact, comparing the HTRA70 time series with the respective one including all three terms from the RHS of Eq. (2), reveals that both the ocean heat storage term and the TOA terms are often of considerable amplitude. Indeed, differences between the black line and the blue line in Fig. 4a indicate periods where all terms of the RHS of Eq. (2) are needed to compensate HTRO70 variations. The respective contributions from the time-derivative of ocean heat content change and TOA radiation are of similar magnitude (Fig. 4b) but the amplitude of the residual appears to be more strongly controlled by the heat content changes. The most prominent example where there is no compensation is the period 2175–2225. HTRO70 anomalies are sustained positive (Fig. 4a) and lead to considerable increase in the heat content change (Fig. 4b) (the green curve is negative here because of the sign convention in Eq. (2)). From 2200 to 2225 HTRA70 anomalies are also positive and the heat surplus has to be radiated off to space leading to negative TOA anomalies (Fig. 4b). At other times, for example around the years 2525, HTRA70 is opposite in sign to HTRO70 but the higher amplitude of HTRA70 has to be compensated by contributions mainly from the TOA term (Fig. 4b).

The implied atmospheric heat transports calculated from Eq. (1) is very similar, but not identical to the advective energy transport according to Eq. (3) (Fig. 4c). This is due to different assumptions, e.g. neglecting diffusive transports in Eq. (3) or neglecting heat storage variations in the atmosphere in Eq. (2). Equation 3 allows us to discriminate between the dry static (first and second term in the integrand) and latent energy (third term) transports. For the decadally smoothed time series, Fig. 4c indicates that the variability is mostly determined by the dry static part. However, considerable contributions are seen, for example, around the year 2200 and the year 2225. This indicates that contributions from latent heat changes may disturb the compensation mechanism.

3.1.3 Long-term changes in the relation between oceanic and atmospheric heat transports

To better quantify the relation between the ocean and atmosphere transports, Van der Swaluw et al. (2007) introduced a compensation rate (CR) in percentage of the maximum local transport;

$$ CR = (1 - V) \times 100\% $$
(5)

with

$$ \begin{gathered} V = \left| {dH_{\text{tot}} } \right|/W, \hfill \\ W = {\text{ max(|}}dHTRO |,d|HTRA| ), \hfill \\ \left| {dH_{tot} } \right| = \left| {dHTRA + dHTRO} \right| \hfill \\ \end{gathered} $$

and dH denoting the anomaly of the considered heat transport to the time mean. Van der Swaluw et al. found a latitudinal maximum CR of 55% at 70°N averaged over their 341-year-long control integration applying a 15-year running mean. Also in ECHAM5/MPIOM the CR is highest around 70°N but the time-average CR is only 28%. Displaying the CR for the entire time series (Fig. 5a), it is evident that CR is changing over time and that there are decades to centuries with relatively high CR, but also periods without any or even negative (i.e., amplification instead of compensating heat transport anomalies). This is also the explanation for the somewhat smaller correlation in our model compared to HadCM3. Running correlations between the ocean and atmosphere anomalies (Fig. 5b) confirm that, over centuries, the anticorrelation is quite strong with similar values (−0.8) as reported by van der Swaluw et al. (2007) but there are considerable deviations throughout the integration. Most notable is the period around the simulation year 2220 where the mode of compensation breaks down completely and ocean and atmospheric heat transport are not or even positively correlated. We emphasize that this is not a spin-up phenomenon since the coupled model was run into quasi-equilibrium before. Comparing the running correlations for the dry static energy and the total energy again points to the period around the year 2200 where there are pronounced contributions from the latent heat component.

Fig. 5
figure 5

Time series describing the long-term changes in the relation between oceanic and atmospheric heat transports 70°N. a Compensation rate of the atmospheric and oceanic heat transports for the 11-year (thin line) and 51-year (thick line) running means; the black horizontal line is the time average (28%). b Running correlation based on a 50-year sliding window between the oceanic heat transport and (solid) the total atmospheric and (dashed) the dry static energy transport

Full size image

3.2 Regional response to heat transport variations

In the following, we separate the analysis for the time period in the simulation where we have persistently strong negative correlation between atmospheric and oceanic heat transport anomalies (simulation years 2275–2625) and the earlier part of the simulation where ocean and atmosphere tend to act in concert (2175–2275). For the years 2275–2625 we perform regression analyzes between HTRO70 and various variables to study the interactions between the marine cryosphere, the ocean, and the atmosphere. These manifest themselves in strong anomalies in sea ice cover, ocean-atmosphere heat fluxes and subsequent responses of the pressure field. The regression between the anomalous ocean heat transports and the sea level pressure (SLP) (Fig. 6a) and the surface air temperature (Fig. 6b) indicate that the center of air-sea interaction in this model is located in the Svalbard/Barents Sea area. Here sea-ice variability (Fig. 6d) is strongly influenced by decadal-scale ocean heat transport variations in the Barents Sea opening. In addition, sea-level pressure anomalies between Svalbard and Novaya Semlya favor southerly winds and lower-than normal ice import into the Barents Sea (Koenigk et al. 2008). Anomalous ocean-air heat fluxes (Fig. 6c) lead to considerable warming and the evolution of a thermal low. The SLP pattern is somewhat different compared to the one discussed in Van der Swaluw et al. (2007): in HadCM3 the sea ice and heat flux variability is largest in the central Greenland Sea where there is also the center of the negative SLP anomaly. In our simulation, the SLP regression pattern based on decadal running means almost resembles the model’s Arctic Oscillation (AO) or Northern Annular Mode pattern, i.e. the first EOF of SLP 20–90°N based on winter mean fields (see Sect. 3.4). The response with a low-pressure center over Svalbard and the Barents Sea resembles the feedback mechanism discussed in Bengtsson et al. (2004): positive heat transport anomalies in the Barents Sea opening lead to a SLP pattern that favors enhanced oceanic transports onto the Barents Shelf. A similar response pattern was identified in a control simulation with the Community Climate Model by Goosse and Holland (2005). While these authors emphasize the local character of this air-sea interaction, it is interesting to note that there are significant correlations at least also for the centers of action of positive SLP response in the Bay of Biscay and south of the Aleutian Islands. As we show below, the Pacific sector plays a particular role in the compensation mechanism. Overall, the SAT response to oceanic heat transport variations is almost dipolar with anomalous warm condition in the Siberian Arctic, Scandinavia, and central Europe and cold conditions in the North American part of the Arctic. In particular, SAT variations are strongest in the Barents Sea but the associated SLP response with westerly winds over northern Russia leads to considerable warming over Siberia. In contrast, the North American Arctic, the Labrador Sea and the Sub Polar Gyre (SPG) region of the North Atlantic experience cooling. There is also a shift in the position of the Gulf Stream (Fig. 6c) with local effects on the ocean atmosphere heat fluxes and possible effects for the interdecal variability of the ocean circulation. Moreover, the NAO/AO-like SLP pattern in the North Atlantic is associated with winds that favor convection in the Labrador Sea. This could possibly add a feedback that could contribute to the specific time-scale of the oceanic circulation and heat transport variations: Enhanced Labrador Sea deep water formation would lead to a stronger MOC and positive ocean heat transport anomalies. However, the details of the mechanisms determining the time-scale of the large-scale ocean circulation and heat transport variations are beyond the scope of this paper.

Fig. 6
figure 6

Regression of various fields with the ocean heat transport at 70°N (HTRO70) when HTRO70 is leading by one year: a SLP (Pa per standard deviation (std.dev) of HTRO), b SAT (K per std.dev HTRO70), c surface heat flux (W m−2 per std.dev HTRO70), and (d) sea ice concentration (% per std.dev HTRO70). Dashed lines indicate regions where the significance exceeds 95% according to a t test

Full size image

To further elucidate the relation between the ocean heat transport anomalies and the atmospheric role in redistributing heat in high northern latitudes we analyze the atmospheric energy transport variations at 70°N as a function of longitude (Fig. 7). The longitudinal variations of the time-mean HTRA′ (dashed line) image the large-scale atmospheric circulation and is a time integral of the structures depicted in Fig. 2. The zonally integrated 1.55 PW is the residual of strong northward and southward components. While the regression of HTRO70 with the zonally averaged HTRA70 gives about −0.01 PW atmospheric heat transport anomaly per HTRO standard deviation, the longitudinally resolved regression (Fig. 7) reveals that this is a residual of southward and northward anomalies. There is anomalous export of heat east of 30°E. In particular, northern Russia and Siberia are warmed by anomalous northerly winds that carry positive temperature anomalies from the Barents Sea/Kara Sea over to the Eurasian land masses. Another pronounced negative anomaly is centered around 160°W where the weakening of the Aleutian Low leads to a reduction of poleward winds and heat transports. On the other hand, local northward anomalies in atmospheric heat transport are seen over northern Canada and in the Greenland Sea/Barents Sea area. Thus, even though the integrated HTRA70 anomaly is negative in response to a positive HTRO70 anomaly, the warming in the Atlantic sector of the Arctic and in particular in the Svalbard/Barents Sea region is amplified by two (local) effects: the resulting SLP gradient accelerates the inflow of warm Atlantic water onto the Barents Shelf (Bengtsson et al. 2004) and the large-scale atmospheric circulation pattern carries warm North Atlantic air into the Greenland Sea/Barents Sea sector. Van der Swaluw et al. (2007) emphasize that the mechanisms behind the reduction of HTRA70 in response of a positive HTRO70 is the reduced transport due to transient eddies caused by the diminished meridional temperature gradient and reduced baroclinicity in the atmosphere. However, somewhat counterintuitive, Fig. 7 indicates that, in our simulation, it is not the transient eddy transport associated with the Atlantic storm track where we find a reduction of poleward heat transport but the respective field in the Pacific sector. On the contrary, the warming of the Svalbard/Western Barents Sea sector through atmospheric heat transport is associated with an increase of cyclone activity as expected from an positive NAO/AO–like atmospheric circulation anomaly (Fig. 6a). Van der Swaluw et al. discussed the transient eddy response only in a zonally-averaged context (their Fig. 7a). The SLP response to positive ocean heat transport anomalies (their Fig. 7b) that is characterized by a low pressure centre in the Greenland Sea, however, suggest that there should be anomalous northward flow along the Norwegian coast and, hence, also in the HadCM3 simulation the atmospheric heat transport anomaly in the Barents Sea sector should be positive.

Fig. 7
figure 7

Regression between HTRO70 and the vertically integrated atmospheric heat transports anomalies as a function of longitude (solid line, left axis, units are 109 W m−1 per std. dev. of HTRO70) along the 70°N latitude circle from the period 2276–2625 when HTRO70 is leading by 1 year. Positive values indicate anomalous northward transport across 70°N. The dashed line is the mean vertically integrated heat transport along 70°N (right axis, units are 109 W m−1)

Full size image

In summary, even though the interaction between ocean and atmosphere takes mainly place in the Atlantic sector, the Pacific sector plays a crucial role in the atmospheric response. The regional differences in the atmospheric circulation response lead to the dipolar temperature response in the Northern Hemisphere SATs (Fig. 6b).

3.3 Heat transport variations and pan-Arctic temperature changes

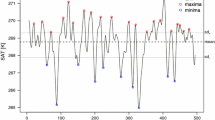
Given the importance of the lateral heat fluxes the issue of compensation is important for the total Arctic heat budget. If the compensation were total, this mechanism would provide a moderating influence on decadal-scale climate variation and counteract an amplification of Arctic climate change as it was observed, for example, in the 1930s to 1940s warming. In the following we analyze the effect of the lateral heat transport anomalies on the simulated Arctic climate. As an integral measure for decadal-scale Arctic climate variations we use the annual mean surface air temperature (SAT) averaged over 70–90°N. The smoothed SAT time series exhibit decadal-scale anomalies of up to 0.7°C (Fig. 8). The order of magnitude of these variations appears quite realistic compared to analyzes of the 20th century temperature record (e.g., Kuzmina et al. 2008). As demonstrated above, the ocean heat transport variations severely impact the Atlantic domain of the Arctic, but warming in the European/Siberian Arctic associated with positive ocean heat transport anomalies is partly compensated by cooling in the North American Arctic. Therefore, the correlation between HTRO70 and the Arctic SAT is relatively small (0.3). On the other hand, SAT anomalies are significantly correlated (0.51) to the sum of HTRO70 and HTRA70 (henceforth HTRSUM) when the combined heat transport anomalies lead by 3 years (Fig. 8). Moreover, correlation between HTRSUM and the time derivative of the SAT is similarly high (0.53) (not shown). The SAT record also confirms that the compensation mechanism tends to damp Arctic climate variations. At times of relatively high CR (e.g. year 2275–2375) the anomalies in Fig. 8 rarely exceed the standard deviation of 0.28°C.

Fig. 8
figure 8

Relation of the sum of atmospheric and oceanic heat transport anomalies at 70°N (solid line, left axis) and the integrated Arctic SAT anomalies (dashed line, right axis). The correlation between both time series is 0.51

Full size image

The regression pattern of HTRSUM and the SAT field (Fig. 9) is quite similar to the one in Fig. 6b in terms of the general features, but the polar cap is now more dominated by positive temperature anomalies covering larger parts of eastern Siberia and the Bering Strait region. There are less pronounced negative anomalies over Alaska, northern Canada, and Greenland. A regression of HTRA70 and SAT (not shown) revealed that these features are related to positive HTRA70 anomalies in the East Siberian/Pacific sector.

Fig. 9
figure 9

Regression of HTRSUM and the surface air temperature (K per std. dev. HTRSUM). Dashed lines indicate regions where the significance exceeds 95% according to a t test

Full size image

3.4 Variations of the large-scale atmospheric circulation patterns

The prominent role of the Pacific sector and the North Pacific SLP anomaly brings up the question what determines the variations there. One likely explanation is that the large-scale atmospheric circulation and its associated heat transport anomalies along 70°N, and in particular in the Pacific sector, is not entirely controlled by the BC mechanism. Other mechanisms or atmospheric variability patterns obviously play an important role, at least at times. Therefore we calculate Empirical Orthogonal Functions (EOFs) and associated time series of principal components (PCs) based on the decadally smoothed SLP (Fig. 10). Several publications have emphasized that the major patterns of variance for the Northern Hemisphere near surface atmospheric circulations can be identified in an EOF analysis of annual (winter) SLP from 20 to 90°N. While Quadrelli and Wallace (2004) and Wu and Strauss (2004) emphasized the two leading modes, Overland and Wang (2005) showed that also the third pattern contributed to particular SAT trends in the 20th century. The simulated decadal-scale patterns bear some resemblance to the observed (seasonal) modes derived from observations (e.g. Overland and Wang 2005). The first pattern (Fig. 10a), which explains more than 22% of the variance, resembles strikingly the regression pattern depicted in Fig. 6a. Moreover, the principal component (PC) time series of EOF1 and HTRO70 are significantly correlated (>0.5). Even though the EOF1 SLP minimum is located near Svalbard and not near Iceland as in the observations (and in the respective simulated EOF based on winter mean SLP, not shown), we call it an AO-like pattern. The second pattern (Fig. 10b) with its characteristic low-pressure center near the Aleutians for the positive phase resembles the second EOF in Overland and Wang (2005). Following their notation, we call it a Pacific North American (PNA)-like pattern (Quadrelli and Wallace 2004). The two leading EOFs explain almost 40% of the decadal variability. The third and fourth (Fig. 10c, d) EOFs are quite similar in their explained variance and their ranking is therefore questionable. However, the fourth EOF has some features that resemble the negative phase of the third EOF described in Overland and Wang (2005).

Fig. 10
figure 10

The first four (a–d) empirical orthogonal functions (EOF) of the decadal anomalies of SLP north of 20°N for the entire experiment. The explained variance of the respective modes is 22.8, 17.2, 9.9, and 9.2%. An 11-year running mean was applied to all fields prior to the analysis

Full size image

A regression of the associated PCs onto the SAT field (not shown) reveals that the first PC time series is associated with a dipolar temperature pattern, similar to the regression pattern in Fig. 6b. The respective regression based on the PC2 is characterized for the positive phase by a more Arctic wide warming with maxima in the Barents Sea, East Greenland, and the Alaska/Bering Strait region. The prominent role of the EOF2 pattern for Arctic climate variations is emphasized by the fact that it’s PC is significantly (r = 0.55) correlated to the integrated Arctic SAT (Fig. 11a) while the other PCs are not. Again, we find that this relation is not stationary in time. In particular during the period 2275–2400, when there is the highest anti-correlation between HTRO70 and HTRA70, the correspondence between the PC2 time series and the SAT is particularly low, whereas it is particularly high during the years 2425–2625.

Fig. 11
figure 11

a Normalized time series of the Arctic SAT (solid) together with the principal component time series of the second EOF of decadal SLP anomalies. The correlation between both time series is 0.55. b Phase space diagram from the EOF analyses. The axes correspond to the principal component time series of the first and second EOF of SLP (Fig. 10). Crosses indicate situations where the compensation rate between HTRO70 and HTRA70 is particularly high (exceeding the mean value plus one standard deviation) and open squares relate to situations where the compensation rate is correspondingly low

Full size image

A phase-space diagram that is based on the two leading EOFs (Fig. 11b) suggests that there is a stronger contribution from the second EOF pattern at times when the compensation rate is particularly low.

In summary, we find that there is an atmospheric circulation pattern associated with the compensation mechanism (Figs. 6a, 10a). In terms of the atmospheric heat transport variations at 70°N the compensation depends strongly on the Pacific sector where also the second EOF has a pronounced center of action and the relative importance of the leading patterns is changing with time. The reason for these shifts are quite hard to identify but the particular importance of the Pacific center of action suggest some similarity to the observed variation in the role of the first and second EOF for the SLP in the North Pacific (Wallace and Thompson 2002; Zhang et al. 2008; Zhao and Moore 2009). These authors talk about “regime shifts” but the mechanisms behind these shifts in the atmospheric circulation regimes are difficult to identify. This requires dedicated model studies, applying, for example idealized forcing or partially coupled experiments where the variability in certain region is suppressed. Recently, Jia et al. (2009) have performed experiments using a simplified atmospheric general circulation model and analyzed the response to different idealized tropical Pacific forcings. They find that there are different propagation pathways for disturbances in the eastern and western tropical Pacific, respectively. However, to find out if the mechanisms discussed by Jia et al. (2009) are also at work in our more complex model would require carrying out such sensitivity studies for which we don’t have the computational resources at hand.

3.5 Relation to observed climate variability

Here we explore the role of the presence or absence of the heat transport compensation in producing pronounced Arctic-wide climate variations, such as the observed 1930s to 1940s warming. The strongest simulated Arctic-wide temperature anomalies on the decadal scale exceed 0.7°C (Fig. 8). The 20th century Arctic temperature record displayed in Kuzmina et al. (2008) for 5-year running means show that the early-century warming had amplitude of about 1°C (60°–90°N average). In the simulation, strong warming or cooling events are associated either with incomplete compensation (such as the peaks in the years 2480 and 2520) or, in an extreme case around the year 2220, with a situation where HTRO70 and HTRA70 are both of the same sign. An inspection of the most prominent warming around the year 2220 show the following sequence of events: Between 2113 and 2118 (Fig. 12 a, b) HTRO70 is positive (Fig. 4a) and the associated extremely positive AO-like SLP pattern leads to a further warming of the Atlantic sector and the Barents Sea in particular. The following years (2219–2224, Fig. 12 c, d) are characterized by relatively high pressure over Scandinavia and a low-pressure trough that extends from Britain westward over Greenland and northern Canada. This SLP distribution has some elements of the negative phase of the 4th EOF (Fig. 10d). Temperatures are anomalously warm in Eastern Siberia, Alaska, and the central Arctic, but also between Iceland and Greenland and in the Labrador Sea. Thereafter, in the following pentad (Fig. 12 e, f), the SLP anomalies carry features of the positive phase of the PNA-like EOF2 pattern with slightly shifted centers of pressure anomalies: A low-pressure anomaly extending into Russia and Siberia and a pronounced low anomaly south the Aleutian Islands. The pressure field associated with the latter carries warm air into western Canada.

Fig. 12
figure 12

Anomalies of (left) SLP and (right SAT) for the time periods (a, b) 2213–2219, (c, d) 2219–2224, and (e, f) 2224–2229

Full size image

It is interesting to compare this sequence of events with the description of the “real” decades of the 1920s, 1930s, and 1940s by Overland and Wang (2005). They summarize that the early period, roughly 1920–1927, was dominated by a positive phase of AO, or more locally the North Atlantic Oscillation. The following years were characterized by a particular pattern of SLP and temperature anomalies with warm temperatures in both Europe and west Greenland associated with a low-pressure trough over Iceland and Canada, a feature which carries some elements of the third EOF of Northern Hemisphere SLP. The final period (1940–1942) had warm surface temperatures in Eastern Siberia, Alaska, and northeastern Canada related to SLP anomalies with resemblance to the positive PNA pattern. We do not claim that our experiment gives an exact picture of the real early 20th century climate evolution but the model results indicate that a strong warming event may be the result of a combination of climate patterns with different underlying mechanisms. The variations in the oceanic heat transport alone (e.g., Polyakov and Johnson 2000) or associated with local feed back effects (Bengtsson et al. 2004) would not be sufficient to explain a sustained warming. In the early part of the warming, the atmosphere responds to the HTRO70 anomalies with compensation (Fig. 4a), but, while HTRO70 anomalies remain positive, HTRA70 anomalies become also positive due to the shift in the circulation regime. Therefore we conclude that ocean and atmospheric heat transport must act in concert to achieve an Arctic-wide warming of the magnitude observed in the early to mid 20th century.

Sorteberg and Kvingedal (2006) studied the atmospheric forcing on the Barents Sea winter ice extent for the period 1967–2002 by analyzing the path and number of synoptic cyclones entering the Arctic. They identified two regions that influence the Barents Sea ice extent: the variability of the northward-moving cyclones traveling into the Arctic from the easternmost part of Siberia and the cyclone activity of northward moving synoptic system over the western Nordic Seas. They emphasize that the latter modulate the oceanic heat input into the Barents Sea. They also find that the Nordic Seas component co-varies with the AO/NAO while the East Siberian component does not. These findings are consistent with the model results discussed here. Ocean and atmosphere heat transport anomalies in the Atlantic sector clearly show a pronounced influence on the Barents Sea ice extent and Arctic-wide SAT but contributions from the East Siberian/Pacific sector of the Arctic need to be taken into account. They influence the Barents Sea ice extent by changing Arctic winds and ice advection.

4 Summary and conclusions

In this study we have investigated the decadal-scale variability of atmospheric and oceanic heat transports in a coupled climate model with a focus on their role in shaping the climate of the high northern latitudes. Recent model-based studies have demonstrated that the strong ocean-atmosphere coupling due to variations of the sea ice cover (and the associated enormous heat flux anomalies) could lead to the so-called Bjerknes Compensation where the atmosphere responds with reduced transient eddy transport to positive anomalies in oceanic heat transport. Decadal-scale variations in HTRO and HTRA are indeed anticorrelated most pronounced near 70°N in ECHAM5/MPIOM. The atmosphere responds to positive HTRO anomalies with a modified circulation that leads to increased heat outflow across 70°N towards Siberia and to reduced heat inflow over Alaska and Canada. This results in a dipolar temperature response and a moderation of pan-Arctic temperature changes.

The degree of compensation determines the heat transport anomalies available to modulate the large-scale Arctic climate (defined here as the 70°–90°N SAT average). The combined effect of HTRA and HTRO (HTRSUM) has to be considered to explain decadal-scale warming or cooling trends. In fact, the model simulation suggests that ocean and atmosphere have to act in concert to create drastic temperature changes, such as the early-20th century warming.

While the compensation mechanism is prominent, the compensation rate also changes over longer (century) time scales. These changes are related to shifts in the large-scale atmospheric circulation. The “compensation mode”, associated with the oceanic variations in the Atlantic sector, is characterized by an AO-like SLP pattern that is sometimes overruled by a more PNA-like EOF2 pattern. Consistent with observations, both the AO-like and the PNA-like SLP anomaly pattern influence the SAT and the circulation regimes related to particular combinations of the patterns vary over decadal and longer time scales. A similar conclusion can be drawn from observations of 20th century climate (Overland and Wang 2005). Moreover, analyzing data from 1864 to 1998, Vinje (2001) demonstrated that there is a fairly high correlation between April sea ice in the Barents Sea with the NAO, but this relationship is not stationary over times.

The reasons for these regime shifts are still unknown. One mechanism that has been proposed to be important for the Arctic circulation in general is the phase of the planetary-scale SLP wave 1 (Cavalieri and Häkkinen 2001). Further analysis of the model experiment here and additional sensitivity experiments together with an assessment of how realistically climate models simulate the characteristics of Arctic climate variations and their remote forcing have to be carried out. A key question is how changes (most likely in the tropical Pacific) may interact with the North Atlantic and the North Pacific (e.g., Jia et al. 2009). Another important question that will be addressed in an upcoming paper is the future evolution of the interaction between oceanic and atmospheric heat transports in a global warming context with much reduced ice cover and ice thickness.