A New Proof for a Result of Kingan and Lemos’

Abstract

The prism graph is the planar dual of $K_5 \backslash e$. Kingan and Lemos (Graphs Comb 30:1479–1497, 2014) proved a decomposition theorem for the class of binary matroids with no prism minor. In this paper, we present a different proof using fundamental graphs and blocking sequences.

1 Introduction

Our notation and terminology will generally follow Oxley [7] with one exception: we use $\text{ si }(M)$ (resp. $\text{ co }(M)$) to denote the simplification (resp. cosimplification) of a matroid $M$. A very interesting open problem in matroid theory is to characterize the class of binary matroids without $M(K_5)$ minor. Kingan and Lemos [4] recently obtained a strong partial result where they proved a decomposition theorem for the class of binary matroids without prism ($M^*(K_5\backslash e)$) minors. We will give another proof of their result by using fundamental graphs and blocking sequences. Both their proof and ours make use of a result of Oxley [6] on binary matroids without $P_9$ or $P_9^*$-minors. The matroid $P_9$ is the 3-sum of $F_7$ and $M(K_4)$ with exactly one element deleted from the common triangle. The binary matroid $Z_r$ has $2r+1$ elements and can be represented by the binary matrix $[I_r|D]$ where $D$ has $r+1$ columns labeled $b_1$, $\ldots$, $b_r$, $c_r$. The first $r$ columns of $D$ have zeros in the diagonals and ones elsewhere. The last column of $D$ is all ones.

Theorem 1.1

(Oxley [6]) If $M$ is a 3-connected binary matroid with no minor isomorphic to $P_9$ or $P_9^*$, then either

• (1) $M$ is regular; or

• (2) $M$ is isomorphic to $F_7$, $F_7^*$, $Z_r$, $Z_r^*$, $Z_r \backslash b_r$, or $Z_r \backslash c_r$ for some $r \ge 4$.

The next theorem is the main result in [4].

Theorem 1.2

Let $M$ be a 3-connected non-regular binary matroid with no $M^*(K _5 \backslash e)$-minor. Then one of the following holds:

• (1) $M$ is isomorphic to $Z_r$, $Z_r^*$, $Z_r \backslash b_r$, or $Z_r \backslash c_r$ for some $r \ge 4$;

• (2) $M$ has a 3-separation that is induced by a non-minimal 3-separation of $P_9$.

• (3) $M$ is isomorphic to the rank-6 matroid that is the dual of the generalized parallel connection of $F_7$ with itself across a triangle, with an element of the triangle deleted.

• (4) $M$ has rank at most 5.

Note that the exceptional matroid in Theorem 1.2 part (3) is not internally 4-connected, and it has a 3-separation induced by a non-minimal 3-separation of $P_9^*$. We will use fundamental graphs to prove Theorem 1.3, a weaker version of Theorem 1.2.

Theorem 1.3

Let $M$ be a 3-connected non-regular binary matroid with no $M^*(K _5 \backslash e)$-minor. Then one of the following holds:

• (1) $M$ is isomorphic to $Z_r$, $Z_r^*$, $Z_r \backslash b_r$, or $Z_r \backslash c_r$ for some $r \ge 4$;

• (2) There exists a matroid $N \in \{P_9, P_9^*\}$ such that $M$ has a 3-separation that is induced by a non-minimal 3-separation of $N$.

• (3) $M$ has rank at most 5.

Here is a rough sketch of our proof for Theorem 1.3; refer to Sect. 3 for definitions of the matroids that we use: Let $M$ be an internally 4-connected non-regular binary matroid with no prism minor. By Theorem 1.1, we may assume $M$ has a $P_9$- or $P_9^*$-minor. Then we use a result of Zhou [9] to show that $M$ is either isomorphic to $N_{10}$ or has a $\widetilde{K}_5$-minor. Since $\widetilde{K}_5$ is internally 4-connected, we apply the strong splitter theorem to prove that either $M$ has rank at most 4, or has a minor isomorphic to one of $\widetilde{K}_{5,r_1}$, $\widetilde{K}_{5,r_2}$, $\widetilde{K}_{5,r_3}$, and $\widetilde{K}_{5,r_4}$. Among these four matroids, $\widetilde{K}_{5,r_2}$ is the only one that is not internally 4-connected, so we use blocking sequence to show that if $M$ has a $\widetilde{K}_{5,r_2}$-minor, then $M$ has rank 5. Finally we use the strong splitter theorem to show if $M$ has a $\widetilde{K}_{5,r_1}$, $\widetilde{K}_{5,r_3}$-, or $\widetilde{K}_{5,r_4}$-minor, then $M$ has rank 5.

Note that, the major difference between our proof and Kingan and Lemos’ proof is that we use fundamental graphs to reveal symmetries among elements of a matroid and to generate 3-connected extensions and coextensions; the steps did not require the use of a computer program.

2 Preliminaries

In this section, we present the main techniques that we will use in the proof.

Seymour’s Splitter Theorem is a well-known inductive tool in proving matroid structural theorems. Recently, Kingan and Lemos obtained a stronger version which they call the “Strong Splitter Theorem”.

Theorem 2.1

(Kingan and Lemos [5]) Let $N$ be a 3-connected proper minor of a 3-connected matroid $M$ such that if $N$ is a wheel or whirl, then $M$ has no larger wheel or whirl minor, respectively. Let $m= r(M) - r(N)$. Then there exists a sequence of 3-connected matroids $M_0$, $M_1$, $\ldots$, $M_n$ for some integer $n \ge m$ such that

• (1) $M_0 \cong N$ and $M_n=M$;

• (2) for $k\in \{1,2,\ldots ,m\}$, $r(M_k)=r(M_{k-1})=1$ and $|E(M_k)-E(M_{k-1})| \le 3$; and

• (3) for $k \in \{m+1,\ldots ,n\}$, $r(M_k) = r(M)$ and $|E(M_k)-E(M_{k-1})|=1$.

Moreover, when $|E(M_k)-E(M_{k-1})|=3$ for some $k \in \{1,2,\ldots ,m\}$, $E(M_k) - E(M_{k-1})$ is a triad of $M_k$.

In Seymour’s original version, every step is either a single-element extension or a single-element coextension, while the stronger version states that at most two consecutive single-element extensions occur in the sequence, unless the matroids involved have the same rank; when this happens, $|E(M_k) - E(M_{k-1})| = 3$ and the three new elements form a triad in $M_k$. We further remark that in the case $|E(M_k)-E(M_{k-1})|=2$ for some $k \in \{1,2,\ldots , m\}$, there also exists a special triad in the matroid $M_k$. Assume that $M_{k-1} = M _ k \backslash e /f$. Then $M_k$ has a triad containing both $e$ and $f$. (Since we may assume $M_k \backslash e$ is not 3-connected, as otherwise we can coextend directly from $M_{k-1}$; Since $M_k \backslash e /f = M_{k-1}$ is 3-connected, $f$ is in a series pair of $M_k \backslash e$. Now the claim follows from the fact that $M_k$ is 3-connected.) We will use the Strong Splitter Theorem together with the remark to reduce the number of cases in our proofs.

Since we study only binary matroids, we will use fundamental graphs to represent binary matroids. Let $M= M([I_r|P])$ be a binary matroid and let $B$ be the base of $M$ represented by $I_r$. Now we label the rows of $P$ by elements in $B$ and label columns of $P$ by element of $E\backslash B$. The fundamental graph of $M$ with respect to $B$, denoted by $G_B(M)$, is the bipartite graph with bipartition $(B, E\backslash B)$ and bi-adjacency matrix $P$. When we draw the graph $G_B(M)$, we will use solid vertices to represent elements of $B$ and use hollow vertices to represent elements of $E \backslash B$. Clearly by interchanging solid vertices and hollow ones, we obtain the fundamental graph $G_{E \backslash B}(M^*)$.

Minors and Separation of a binary matroid can be read off from its fundamental graphs. Note that contracting an element $e$ in $B$ is the same as deleting the corresponding row in the matrix $P$, therefore $G_{B \backslash \{e\}} (M /e)$ is obtained from $G_B(M)$ by deleting the solid vertex $e$; similarly, deleting an element $f$ in $E \backslash B$ is the same as deleting the corresponding column in the matrix $P$, so $G_B( M \backslash f)$ is obtained from $G_B(M)$ by deleting the hollow vertex $f$. To delete an element in $B$, or to contract an element in $E \backslash B$, we will require the pivot operation: let $(u,v)$ be an edge of $G_B(M)$ with $u \in B$ and $v \in E \backslash B$. Then $B' = B \bigtriangleup \{u,v\}$ is a base of $M$. The graph $G_{B'}(M)$ is obtained from $G_B(M)$ by the following two-step operation:

• (1) For any $b \in neigh(v) \backslash \{u\}$ and any $c \in neigh(u) \backslash \{v\}$, $b$ and $c$ are adjacent in $G_{B'}(M)$ if and only if they are not adjacent in $G_B(M)$; for all other pairs $b \in B$ and $e \in E \backslash B$, $b$ and $c$ are adjacent in $G_{B'}(M)$ if and only if $b$ and $c$ are adjacent in $G_B(M)$.

• (2) Exchange the labels $u$ and $v$.

We call this operation pivoting on $(u,v)$ in $G_B(M)$.

To delete an element $b \in B$ in $G_B(M)$, we pick an edge incident with $b$ (such an edge exists provided $b$ is not a coloop), pivot on that edge, and then delete the vertex $b$. Contracting an element $c \in E \backslash B$ is done similarly. Therefore, minors of $M$ correspond to induced subgraphs of $G_B(M)$ up to pivoting operations.

A well-known fact about fundamental graphs is that the matroid is connected if and only if the fundamental graph is connected. One may also read off higher order separations of the binary matroid from its fundamental graphs through joins. Let $G$ be a graph. A 1-join in a graph $G$ is a partition $(X,Y)$ of $V(G)$ such that the set of edges with one end in $X$ and the other end in $Y$ induces a complete bipartite graph.

A 2-join of $G$ is a partition $(X,Y)$ of $V(G)$ such that

• (1) there exist non-empty disjoint subsets $X_1$ and $X_2$ of $X$ and non-empty disjoint subsets $Y_1$ and $Y_2$ of $Y$;

• (2) $X_i$ is completely joined to $Y_i$ for $i \in \{1,2\}$; and

• (3) there is no other edge between $X$ and $Y$.

Let $(X,Y)$ be a partition of $V(G)$ such that

• (1) there exist disjoint subsets $X_1$, $X_2$, $X_3$ of $X$ and disjoint subsets $Y_1$, $Y_2$, $Y_3$ of $Y$;

• (2) $X_i$ is completely joined to $Y_j$ and $Y_k$ for $\{i,j,k\} = \{1,2,3\}$; and

• (3) there is no other edge between $X$ and $Y$.

If none of $X_i$ , $Y_i$ with $i \in \{1,2,3\}$ is empty, then the partition $(X,Y)$ is called a 6-join; if exactly one of $X_i$, $Y_i$ with $i \in \{1,2,3\}$ is empty, then the partition $(X,Y)$ is called an M-join.

A rank-2 join is a 2-join, a 6-join, or an $M$-join.

It is not hard to see that a binary matroid $M$ is 3-connected if and only if $G_B(M)$ is connected and has no 1-join $(X,Y)$ with $min(|X|,|Y|) \ge 2$. Moreover, $M$ has an exact 3-separation if and only if $G_B(M)$ has a rank-2 join $(X,Y)$ with $min(|X|,|Y|) \ge 3$.

Blocking sequences were first defined in [1] and were used extensively in [2]. We will only use blocking sequences for 3-separations. For $A \subseteq E(M)$, denote $M /(A^c \cap B) \backslash (A ^c \backslash B)$ by $M[A,B]$ where $A^c = E(M) \backslash A$, the complement of $A$. Let $N= M[X \cup Y, B]$ be a minor of $M$ and let $(X,Y)$ be an exact 3-separation of $N$. A sequence $v_1$, $v_2$, $\ldots$, $v_p$ of elements of $E(M) \backslash (X \cup Y)$ is a blocking sequence for $(X,Y)$ with respect to $B$ if

• (1) $(X, Y \cup \{v_1\})$ is not a 3-separation of $M[X \cup Y \cup \{v_1\}, B]$;

• (2) $(X \cup \{v_i\}, Y \cup \{v_{i+1}\})$ is not a 3-separation of $M[X \cup Y \cup \{v_i, v_{i+1}\}, B]$ for all $i \in \{1,2,\ldots , p-1\}$;

• (3) $(X \cup \{v_p\}, Y)$ is not a 3-separation of $M[X \cup Y \cup \{v_p\}, B]$; and

• (4) no proper subsequence of $v_1$, $v_2$, $\ldots$, $v_p$ satisfies (1), (2), and (3).

A blocking sequence alternates between elements of $B$ and $E \backslash B$  [2]. The next theorem is also proved in [2].

Theorem 2.2

Let $N= M[X \cup Y, B]$ be a minor of $M$ and let $(X,Y)$ be an exact 3-separation of $N$. Then $(X,Y)$ does not induce a 3-separation in $M$ if and only if there exists a blocking sequence for $(X,Y)$ with respect to $B$.

Let $M[A,B]$ be a minor of $M$. For $x \in E \backslash A$ and $e \in A$, we say $x$ is parallel to $e$ if $x$ and $e$ have the same neighbors in $A$ or $e$ is the only neighbor of $x$ in $A$. The next lemma lists some important properties of a blocking sequence and the proofs can be found in [2, 3].

Lemma 2.3

Let $N=M[X \cup Y, B]$ be a minor of a 3-connected binary matroid $M$ and let $(X,Y)$ be an exact 3-separation of $N$. Let $v_1$, $v_2$, $\ldots$, $v_p$ be a blocking sequence for $(X,Y)$ with respect to $B$. Then

• (1) for $1 \le i \le j \le p$, $v_i$, $\ldots$, $v_j$ is a blocking sequence for the 3-separation $(X \cup \{v_1, \ldots , v_{i-1}\}, Y \cup \{v_{j+1}, \ldots , v_p\})$ of $M[X \cup Y \cup \{v_1, \ldots , v_{i-1}, v_{j+1}, \ldots , v_p\}, B]$;

• (2) If $Y' \subset Y$ with $|Y'| \ge 3$, $(X,Y')$ is an exact 3-separation of $M [ X \cup Y', B]$, and $(X \cup \{v_p\}, Y')$ is not a 3-separation of $M[X \cup Y \cup \{v_p\}, B]$, then $v_1$, $\ldots$, $v_p$ is a blocking sequence for the 3-separation $(X, Y')$ of $M[X \cup Y', B]$;

• (3) Suppose $|X| \ge 4$ and $v_1$ is parallel to $e \in X$ where $e \notin cl(Y)$ and $e \notin cl^*(Y)$ in $N$. If both $e$ and $v_1$ are in $B$ or both are in $E \backslash B$, we define $B'=B$; otherwise we define $B' = B \bigtriangleup \{e, v_1\}$. Then $v_2$, $\ldots$, $v_p$ is a blocking sequence for the 3-separation $(X \cup \{v_1\} \backslash \{e\}, Y)$ of $M[X \cup Y \cup \{v_1\} \backslash \{e\}, B']$, which is isomorphic to $M[X \cup Y, B]$.

• (4) For $1 \le i \le p$, $v_i$ has at least one neighbor in $X \cup Y$.

3 Definitions and the Proof for Theorem 1.3

In this section we first give definitions of some matroids that we use in the paper.

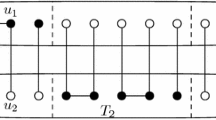
The prism matroid is the dual matroid of $M(K_5 \backslash e)$. Figure 1 shows the prism graph and a fundamental graph of the $M^*(K_5 \backslash e)$.

Fig. 1

The prism graph and a fundamental graph for $M^*(K_5 \backslash e)$

The matroids $\widetilde{K}_5$, $P_{10}$ and $N_{10}$ were all defined in [9]. The matroid $\widetilde{K}_5$ is the unique binary 3-connected single-element extension of $M^*(K_{3,3})$. The matroid $\widetilde{K}_5$ is called $D_2$ in [4].

The matroid $P_{10}$ and $N_{10}$ are both 3-connected coextensions of $P_9$. Figure 2 shows fundamental graphs for $P_9$ and $P_{10}$ and Fig. 3 shows fundamental graphs for $\widetilde{K}_5$ and $N_{10}$. The matroids $P_{10}$ and $N_{10}$ are called $E_4$ and $E_5$, respectively, in  [5].

Fig. 2

Fundamental graphs for $P_9$ and $P_{10}$

Fig. 3

Fundamental graphs of $\widetilde{K}_5$ and $N_{10}$

As we will show in Sect. 3, $\widetilde{K}_5$ has exactly two non-isomorphic 3-connected binary extensions. Figure 4 shows fundamental graphs for both. We call them $\widetilde{K}_{5,c_1}$ and $\widetilde{K}_{5,c_2}$, respectively.

Fig. 4

Extensions of $\widetilde{K}_5$

We will also show in Sect. 3 that $\widetilde{K_5}$ has four non-isomorphic 3-connected coextensions that have no prism minors. Figure 5 shows fundamental graphs for $\widetilde{K}_{5,r_1}$, $\widetilde{K}_{5,r_3}$, $\widetilde{K}_{5,r_4}$; they are all internally 4-connected. Figure 6 shows two different drawings of a fundamental graph for $\widetilde{K}_{5,r_2}$; it is clear from the second drawing that $\widetilde{K}_{5,r_2}$ is not internally 4-connected.

Fig. 5

Three internally 4-connected coextensions of $\widetilde{K}_5$

Fig. 6

A coextension of $\widetilde{K}_5$ that is not internally 4-connected

Now we are ready to present our proof for Theorem 1.3 using fundamental graphs, blocking sequences, and the Strong Splitter Theorem.

First note that, by Theorem 1.1, it suffices to study 3-connected binary matroids with a $P_9$- or a $P_9 ^*$-minor. The proof of the next two lemmas can be found in [9]. Let $X=\{1, 5, 6, 7\}$ and $Y=\{2, 3, 4, 8, 9\}$. Then $(X,Y)$ is a non-minimal 3-separation of $P_9$.

Lemma 3.1

Let $M$ be a 3-connected binary matroid with a $P_9$-minor. If $(X,Y)$ is not induced in $M$, then $M$ must have a $\widetilde{K}_5$-, an $N_{10}$-, or a $P_{10}$-minor.

Lemma 3.2

The matroid $N_{10}$ is a splitter for the class of binary matroids with no minor isomorphic to $\widetilde{K}_5$ or $\widetilde{K_5}^*$.

It follows from Lemma 3.1 and duality that if $M$ is a 3-connected binary matroid with a $P_9^*$-minor and if $(X,Y)$ is not induced in $M$, then $M$ must have a $\widetilde{K_5}^*$-, an $N_{10}$-, or a $P_{10}$-minor.

From now on we assume that $M$ is a 3-connected binary matroid with no $M^*(K _ 5 \backslash e)$-minor. We may further assume that $M$ has a $P_9$- or a $P_9^*$-minor. It follows from Lemma 3.1 that either $(X,Y)$ is induced in $M$, or $M$ has a minor isomorphic to one of $\widetilde{K}_5$, $\widetilde{K_5}^*$, $N_{10}$, and $P_{10}$. Note that the matroid $P_{10}$ has an $M^*(K_5 \backslash e)$-minor (to see this, delete the vertex 8 in the second graph in Fig. 2); also the matroid $\widetilde{K_5}^*$ has an $M^*(K _ 5 \backslash e)$-minor (simply contract 9 in the dual of the first graph in Fig. 3). So we have the following.

Lemma 3.3

Let $M$ be a 3-connected binary matroid with no $M^*(K _ 5 \backslash e)$-minor. If the 3-separation $(X,Y)$ of $P_9$ or of $P_9^*$ is not induced in $M$, then $M$ has a $\widetilde{K}_5$- or an $N_{10}$-minor.

Proof

It follows from Lemmas 3.3 and 3.2 that we may assume that $M$ has a $\widetilde{K}_5$-minor. Since $\widetilde{K}_5$ is internally 4-connected, we will find all 3-connected extensions and coextensions of $\widetilde{K}_5$. We will use $neigh(v)$ to denote the neighbor set of a vertex $v$. Note that, in the fundamental graph of $\widetilde{K}_5$ in Fig. 3, $2$ and $4$ are symmetric to each other; so are $1$ and $3$. So there are at most three 3-connected single-element extensions of $\widetilde{K}_5$ as shown below. None of them can have an $M^*(K_5 \backslash e)$-minor since they all have rank 4.

$neigh(v)$	Name	Remark
$\{2,4\}$	$\widetilde{K}_{5,c_1}$
$\{1,2,4\}$	$\widetilde{K}_{5,c_2}$
$\{1,2,3\}$	$\widetilde{K}_{5,c_3}$	$\cong \widetilde{K}_{5,c_1}$

Next we will find all 3-connected coextensions of $\widetilde{K}_5$. In Fig. 3, we have symmetries among $5$, $6$, $7$ and $8$. Let $v$ be the new solid vertex in a 3-connected coextension of $\widetilde{K}_5$. Then $v$ has at least two neighbors and it is not parallel to any of $1$, $2$, $3$ or $4$. So we have the following cases up to symmetry.

Case 1 $\left| neigh(v)\right| =2$

$neigh(v)$	Prism minor?	Pivots	Deletions
$\{5,6\}$	Yes	$(3,10), (v,5)$	$3, 7$
$\{5,7\}$	Yes	None	$9, 10$
$\{5,8\}$	No; $\widetilde{K}_{5,r_1}$
$\{5,9\}$	Yes	$(v,5)$	$7, 10$
$\{5,10\}$	Yes	$(3,6), (v,5)$	$3, 9$
$\{9,10\}$	Yes	$(v,10)$	$6, 8$

Case 2 $\left| neigh(v)\right| =3$

$neigh(v)$	Prism minor?	Pivots	Deletions
$\left\{ 5,6,7\right\}$	Yes	$(4,9), (v,5)$	$4, 6$
$\left\{ 5,8,9\right\}$	Yes	$(4,9), (v,5)$	$4, 6$
$\{5,7,9\}$	Yes	$None$	$9, 10$
$\{5,6,10\}$	No; $\cong \widetilde{K}_{5,r_2}$
$\{5,8,10\}$	Yes	$(4,7), (v,10)$	$4, 5$
$\{5,7,10\}$	Yes	$None$	$9, 10$
$\{5,9,10\}$	Yes	$(v,10)$	$5, 7$

Case 3 $\left| neigh(v)\right| =4$

$neigh(v)$	Prism minor?	Pivots	Deletions
$\{5,6,7,8\}$	Yes	$(2,5), (4,7)$	$6, 8$
$\{5,6,7,9\}$	Yes	$(4,9), (v,6)$	$4, 5$
$\{5,6,7,10\}$	Yes	$(3,7), (v,5)$	$3, 10$
$\{5,6,9,10\}$	Yes	$(3,9), (v,5)$	$3, 6$
$\{5,7,9,10\}$	Yes	$None$	$9, 10$

Case 4 $\left| neigh(v)\right| =5$ or $6$

$neigh(v)$	Prism minor?	Remark
$\{6,7,8,9,10\}$	No	$\cong \widetilde{K}_{5,r_1}$
$\{5,6,7,8,9\}$	No	$\widetilde{K}_{5,r_3}$
$\{5,6,7,8,10\}$	No	$\widetilde{K}_{5,r_2}$
$\{5,6,7,8,9,10\}$	No	$\widetilde{K}_{5,r_4}$

Lemma 3.4

Let $M$ be a 3-connected matroid with a $\widetilde{K}_5$-minor and with no $M^*(K_5\backslash e)$-minor. If $r(M) \ge 5$, then $M$ has a minor isomorphic to one of $\widetilde{K}_{5,r_1}$, $\widetilde{K}_{5,r_2}$, $\widetilde{K}_{5,r_3}$, and $\widetilde{K}_{5,r_4}$.

Proof

It follows from the Strong Splitter Theorem that $M$ has a 3-connected minor $M'$ such that $M'$ has a $\widetilde{K}_5$-minor, $r(M') = 5$, and $11 \le |E(M')| \le 13$. Clearly we are done if $|E(M')|=11$ as $\widetilde{K}_{5,r_1}$, $\widetilde{K}_{5,r_2}$, $\widetilde{K}_{5,r_3}$, and $\widetilde{K}_{5,r_4}$ are all the 3-connected single-element coextensions of $\widetilde{K}_5$ with no $M^*(K_5\backslash e)$-minor. So we have the following two cases.

Case 1: $|E(M')|=12$.

In this case $M'$ is obtained from $\widetilde{K}_5$ by an extension and then a coextension. Suppose that $M' \backslash v /f \cong \widetilde{K_5}$. Then we may assume that $M' \backslash v$ is not 3-connected as otherwise $M'$ contains one of the 3-connected coextensions of $\widetilde{K}_5$ as a minor and hence the lemma holds. Therefore, $M' \backslash v$ is a series coextension of $\widetilde{K}_5$. In term of the fundamental graph of $M' \backslash v$, $f$ either has only one neighbor, or it has the same neighbor set with another element in the base. Since $M'$ is 3-connected and $\widetilde{K}_5$ has exactly two non-isomorphic extensions, we have the following subcases up to symmetry.

$neigh(v)$	$neigh(f)$	Minor	Pivots	Deletions
$\{2,4\}$	$\{5, v\}$	Prism	$(4,8), (f,5)$	$4, 9, 10$
$\{2,4\}$	$\{9, v\}$	Prism	$(f,v)$	$6, 8, 10$
$\{2,4\}$	$\{10, v\}$	Prism	$None$	$6, 8, 9$
$\{2,4\}$	$\{5,6,9\}$	Prism	$(f,5)$	$6, 7, 8$
$\{2,4\}$	$\{5,8,9,10,v\}$	Prism	$(4,8), (f,10)$	$4, 5, 9$
$\{1,2,4\}$	$\{5,v\}$	Prism	$(3,10), (f,5)$	$6, 7, 8$
$\{1,2,4\}$	$\{6,v\}$	Prism	$(1,5)$	$8, 9, 10$
$\{1,2,4\}$	$\{9,v\}$	Prism	$(4,8), (f,v)$	$4, 6, 10$
$\{1,2,4\}$	$\{10,v\}$	Prism	$(4,8)$	$5, 7, 9$
$\{1,2,4\}$	$\{5,8,9,10\}$	Prism	$(1,10), (2,5)$	$2, 8, 9$
$\{1,2,4\}$	$\{5,6,9\}$	Prism	$(4,v)$	$4, 6, 7$
$\{1,2,4\}$	$\{6,7,9,10,v\}$	Prism	$(4,v)$	$4, 6, 7$

Case 2: $|E(M')|=13$.

In this case $M'$ is obtained from $\widetilde{K}_5$ by two extensions and then a coextension and $E(M')-E(\widetilde{K_5})$ is a triad of $M'$. So $M'$ is obtained by extending twice then completing a triad using the two extended elements. Let $M' /f \backslash v, w \cong \widetilde{K_5}$. Note that in the fundamental graph of $\widetilde{K}_{5,c_1}$, we have symmetries among vertices $1$, $2$, $3$, and $4$. So we have the following cases up to symmetry.

$neigh(v)$	$neigh(w)$	$neigh(f)$	Minor	Pivots	Deletions
$\{2,4\}$	$\{1,2,3\}$	$\{v,w\}$	Prism	$(1,5)$	$6, 8, 9, 10$
$\{1,2,4\}$	$\{2,3,4\}$	$\{v,w\}$	Prism	$(4,8), (f,v)$	$5, 7, 9, 10$
$\{1,2,3\}$	$\{1,3,4\}$	$\{v,w\}$	Prism	$(3,7), (f,w)$	$6, 8, 9, 10$
$\{1,2,3\}$	$\{1,2,4\}$	$\{v,w\}$	Prism	$(3,v), (4,w)$	$3, 4, 9, 10$

The next lemma will help us reduce a large number of case checking in the rest of the proof.

Lemma 3.5

Let $M$ be a matroid obtained from $\widetilde{K}_5$ by two consecutive 3-connected coextensions. Then $M$ has an $M^*(K_5 \backslash e)$-minor.

Proof

As we can see from the list of coextensions of $\widetilde{K}_5$, there are eight ways to coextend $\widetilde{K}_5$ without producing an $M^*(K_5\backslash e)$-minor and they yield four non-isomorphic coextensions of $\widetilde{K}_5$. Suppose that $M /u, v = \widetilde{K_5}$. It follows from unique representability and symmetry that it suffices to check the following cases; they all have an $M^*(K_5\backslash e)$-minor as shown in the table below.

$neigh(u)$	$neigh(v)$	Prism Minor?	Pivots	Deletions	Contraction
$\{5,6,7,8,10\}$	$\{5,8\}$	Yes	$(v,5)$	$7, 10$	$2$
$\{5,6,7,8,10\}$	$\{5,6,10\}$	Yes	$(1,10)$	$1, 9$	$3$
$\{5,6,7,8,10\}$	$\{6,7,8,9,10\}$	Yes	$(v,10)$	$5, 7$	$10$
$\{5,6,7,8,10\}$	$\{5,6,7,8,9\}$	Yes	$(v,8)$	$6, 10$	$8$
$\{5,6,7,8,10\}$	$\{5,6,7,8,9,10\}$	Yes	$(v,10)$	$6, 8$	$10$
$\{5,6,7,8,9,10\}$	$\{5,8\}$	Yes	$(4,9)$	$4, 10$	$2$
$\{5,6,7,8,9,10\}$	$\{6,7,8,9,10\}$	Yes	$(v,7)$	$9, 10$	$7$
$\{5,6,7,8,9,10\}$	$\{5,6,7,8,9\}$	Yes	$(u,10), (v,9)$	$6, 8$	$9$
$\{5,6,7,8,9\}$	$\{5,8\}$	Yes	$(v,8)$	$7, 9$	$8$
$\{5,6,7,8,9\}$	$\{6,7,8,9,10\}$	Yes	$(v,7)$	$9, 10$	$7$
$\{5,8\}$	$\{6,7\}$	Yes	$(4,9)$	$4, 10$	$2$
$\{5,8\}$	$\{6,7,8,9,10\}$	Yes	$(v,10)$	$6, 7$	$10$

Next we list all 3-connected single-element extensions of $\widetilde{K}_{5,r_1}$. See Fig. 5 for a fundamental graph of $\widetilde{K}_{5,r_1}$. Let $u$ be the extension element. By symmetry, we have the following cases.

$neigh(u)$	Prism Minor?	Pivots	Deletions
$\{1,2\}$	Yes	$(2,u)$	$2, 9, 10$
$\{1,v\}$	Yes	$(4,7), (v,u)$	$4, v, 6$
$\{2,4\}$	Yes	$(4,u), (v,5)$	$4, 7, 10$
$\{2,v\}$	Yes	$(3,10)$	$5, 6, 7$
$\{3,v\}$	No; $\widetilde{K}_{5,r_1,c_1}$
$\{1,2,3\}$	Yes	$(2,u)$	$2, 9, 10$
$\{1,2,4\}$	No; $\widetilde{K}_{5,r_1,c_2}$
$\{1,3,v\}$	Yes	$(4,7), (v,u)$	$4, 5, 10$
$\{2,3,v\}$	Yes	$(2,u)$	$2, 9, 10$
$\{2,4,v\}$	No; $\widetilde{K}_{5,r_1,c_3}$
$\{2,3,4\}$	Yes	$(4,u), (v,5)$	$4, 7, 10$
$\{1,2,3,v\}$	No; $\cong \widetilde{K}_{5,r_1,c_1}$
$\{1,2,4,v\}$	Yes	$(2,u)$	$2, 6, 7$
$\{2,3,4,v\}$	No; $\widetilde{K}_{5,r_1,c_4}$
$\{1,2,3,4,v\}$	Yes	$(4,u)$	$4, 6, 7$

Now we are ready to prove the next lemma.

Lemma 3.6

Let $M$ be a matroid with a $\widetilde{K}_{5,r_1}$-minor. If $M$ has no $M^*(K_5\backslash e)$-minor, then $M$ has rank $5$.

Proof

By Lemma 3.5 and the Strong Splitter Theorem, it suffices to show that (1) every matroid obtained from $\widetilde{K}_{5,r_1}$ by a 3-connected extension and then a 3-connected coextension will have an $M^*(K_5 \backslash e)$-minor; (2) every matroid obtained from $\widetilde{K}_{5,r_1}$ by two 3-connected extensions and then the coextension that forms a triad with the two extended elements will have an $M^*(K_5 \backslash e)$-minor.

It follows from the table above that $\widetilde{K}_{5,r_1}$ has four non-isomorphic 3-connected extensions. So there are four cases for (1). In each case we let $w$ be the coextension element. So we have $M /w \backslash u \cong \widetilde{K}_{5,r_1}$. Again, we may assume that $M \backslash u$ is not 3-connected, that is, $w$ is parallel to an element in $M \backslash u$. The next four tables show the single-element coextensions $\widetilde{K}_{5,r_1,c_1}$, $\widetilde{K}_{5,r_1,c_2}$, $\widetilde{K}_{5,r_1,c_3}$, and $\widetilde{K}_{5,r_1,c_4}$, respectively.

$neigh(u)$	$neigh(w)$	Prism Minor?	Pivots	Deletions	Contraction
$\{3,v\}$	$\{5,u\}$	Yes	$(4,8)$	$6, 7, 10$	$v$
$\{3,v\}$	$\{6,u\}$	Yes	$(v,5), (w,6)$	$v, 7, 9$	$4$
$\{3,v\}$	$\{9,u\}$	Yes	$(4,7)$	$6, 8, 10$	$2$
$\{3,v\}$	$\{10,u\}$	Yes	$(1,10), (v,u)$	$1, 5, 7$	$4$
$\{3,v\}$	$\{5,8,9,10,u\}$	Yes	$(v,u), (w,10)$	$w, 5, 7$	$u$
$\{3,v\}$	$\{5,6,9,u\}$	Yes	$(w,u)$	$w, 9, 10$	$u$
$\{3,v\}$	$\{6,7,9,10\}$	Yes	$(w,10)$	$6, 7, 8$	$4$
$\{3,v\}$	$\{5,8\}$	Yes	$(w,8)$	$6, 7, 10$	$4$

$neigh(u)$	$neigh(w)$	Prism Minor?	Pivots	Deletions	Contraction
$\{1,2,4\}$	$\{5,u\}$	Yes	$(4,8), (w,u)$	$4, 9, 10$	$8$
$\{1,2,4\}$	$\{6,u\}$	Yes	$(4,u), (w,6)$	$4, 7, w$	$u$
$\{1,2,4\}$	$\{9,u\}$	Yes	$(4,8), (w,u)$	$4, 6, 10$	$v$
$\{1,2,4\}$	$\{10,u\}$	Yes	$(4,7), (w,10)$	$6, 8, 9$	$v$
$\{1,2,4\}$	$\{5,8,9,10\}$	Yes	$(4,u), (v,8)$	$4, 7, 9$	$8$
$\{1,2,4\}$	$\{5,6,9\}$	Yes	$(4,u), (v,8)$	$4, 7, 9$	$8$
$\{1,2,4\}$	$\{6,7,9,10,u\}$	Yes	$(4,9), (w,10)$	$6, 7, 8$	$v$
$\{1,2,4\}$	$\{5,8,u\}$	Yes	$(4,9), (w,u)$	$4, 5, 6$	$v$

$neigh(u)$	$neigh(w)$	Prism Minor?	Pivots	Deletions	Contraction
$\{2,4,v\}$	$\{5,u\}$	Yes	$(4,8), (w,u)$	$4, 9, 10$	$8$
$\{2,4,v\}$	$\{6,u\}$	Yes	$(v,8)$	$v, 7, 10$	$2$
$\{2,4,v\}$	$\{9,u\}$	Yes	$(w,u)$	$6, 8, 10$	$v$
$\{2,4,v\}$	$\{10,u\}$	Yes	$(v,8)$	$5, 6, 7$	$1$
$\{2,4,v\}$	$\{5,8,9,10,u\}$	Yes	$(w,u)$	$7, 8, 10$	$u$
$\{2,4,v\}$	$\{5,6,9\}$	Yes	$(w,6)$	$7, 8, 10$	$6$
$\{2,4,v\}$	$\{6,7,9,10,u\}$	Yes	$(w,7)$	$5, 6, 10$	$7$
$\{2,4,v\}$	$\{5,8\}$	Yes	$(4,u), (w,8)$	$4, 7, 10$	$u$

$neigh(u)$	$neigh(w)$	Prism Minor?	Pivots	Deletions	Contraction
$\{2,3,4,v\}$	$\{5,u\}$	Yes	$(w,5)$	$7, 9, 10$	$1$
$\{2,3,4,v\}$	$\{6,u\}$	Yes	$(w,6)$	$7, 8, 9$	$4$
$\{2,3,4,v\}$	$\{9,u\}$	Yes	$(4,7), (w,u)$	$4, 5, 10$	$v$
$\{2,3,4,v\}$	$\{10,u\}$	Yes	$(v,8), (w,10)$	$5, 7, 9$	$4$
$\{2,3,4,v\}$	$\{5,8,9,10,u\}$	Yes	$(v,u), (w,9)$	$7, 8, w$	$u$
$\{2,3,4,v\}$	$\{5,6,9\}$	Yes	$(v,u), (w,9)$	$v, w, 10$	$u$
$\{2,3,4,v\}$	$\{6,7,9,10\}$	Yes	$(w,10)$	$5, 6, 7$	$4$
$\{2,3,4,v\}$	$\{5,8\}$	Yes	$(w,8)$	$6, 7, 9$	$4$

Next we need to look at the matroids obtained by two extensions and then completing the triad. Suppose that $M /w \backslash u, x \cong \widetilde{K}_{5,r_1}$. By unique representability and symmetry, we have the following cases.

$neigh(u)$	$neigh(x)$	$neigh(w)$	Prism Minor?	Pivots	Deletions	Contraction
$\{3,v\}$	$\{1, 2,3,v\}$	$\{u,x\}$	Yes	$(w,u)$	$5, 7, 9, 10$	$4$
$\{3,v\}$	$\{1,2,4\}$	$\{u,x\}$	Yes	$(4,8)$	$4, 6, 9, 10$	$v$
$\{3,v\}$	$\{2,4,v\}$	$\{u,x\}$	Yes	$(4,9), (w,u)$	$4, 6, 7, 10$	$v$
$\{3,v\}$	$\{2,3,4,v\}$	$\{u,x\}$	Yes	$(w,u)$	$5, 6, 7, 10$	$4$
$\{1,2,4\}$	$\{2,4,v\}$	$\{u,x\}$	Yes	$(4,9), (w,u)$	$4, 5, 8, 10$	$v$
$\{1,2,4\}$	$\{2,3,4,v\}$	$\{u,x\}$	Yes	$(w,u)$	$6, 8, 9, 10$	$1$
$\{2,4,v\}$	$\{2,3,4,v\}$	$\{u,x\}$	Yes	$(w,u)$	$5, 6, 7, 10$	$4$

Next we study matroids that have a $\widetilde{K}_{5,r_2}$-minor. Note that $\widetilde{K}_{5,r_2}$ is not internally 4-connected.

Lemma 3.7

Let $M$ be a matroid with a $\widetilde{K}_{5,r_2}$-minor. If $M$ has no $M^*(K_5 \backslash e)$-minor, then either $M$ is not internally 4-connected or $M$ has rank $5$.

Proof

Suppose that $M$ is internally 4-connected. Then there exists a blocking sequence for the non-minimal 3-separation of $\widetilde{K}_{5,r_2}$. Choose a blocking sequence that is as short as possible. It follows from Lemma 2.3 that such a blocking sequence must have length 1. Let $a$ be the element in the blocking sequence. By Lemma 3.5, we may assume that $a \notin B$. Note that, there are three hidden symmetries in the fundamental graph of $\widetilde{K}_{5,r_2}$ in Fig. 6: pivot on $(1,10)$, pivot on $(10,v)$, and pivot on $(3,10)$. Up to these symmetries, we may assume that $neigh(a) = \{1,2,3,v\}$ or $\{1,2,3,4,v\}$. In the former case, $M$ has an $M^*(K_5 \backslash e)$-minor by pivoting on $(1,8)$, $(4,10)$, $(6,v)$ and then deleting $1$, $5$, and $7$; in the latter case, $M$ has a $\widetilde{K}_{5,r_1}$-minor by pivoting on $(3,a)$, $(1,8)$, $(2,5)$ and then deleting $3$, so by Lemma 3.6, $M$ has rank $5$.$\square$

Note that by deleting vertices $6$ and $8$ in Fig. 6, we get a matroid isomorphic to $P_9^*$, so the non-minimal 3-separation of $\widetilde{K}_{5,r_2}$ is induced by the non-minimal 3-separation of $P_9^*$. Hence if $M$ has $\widetilde{K}_{5,r_2}$-minor and a non-minimal 3-separation that is induced by a non-minimal 3-separation of $\widetilde{K}_{5,r_2}$, then $M$ has a 3-separation induced by the non-minimal 3-separation of $P_9^*$.

Next we list all single-element extensions of $\widetilde{K}_{5,r_3}$. See Fig. 5 for a fundamental graph of $\widetilde{K}_{5,r_3}$. Note that the symmetries between $1$ and $3$, and between $2$ and $4$. So there are eleven cases.

$neigh(u)$	Minor?	Pivots	Deletion(s)
$\{1,2\}$	Prism	$(3,7), (v,8)$	$3, 5, 9$
$\{2,4\}$	Prism	$None$	$6, 8, 9$
$\{1,v\}$	Prism	$(4,9), (v,5)$	$v, 6, 8$
$\{2,v\}$	Prism	$(4,8)$	$5, 6, 7$
$\{1,2,3\}$	$\widetilde{K}_{5,r_1}$	$(3,10), (v,8)$	$6$
$\{1,2,4\}$	$\widetilde{K}_{5,r_1}$	$(3,10), (4,7), (v,5)$	$4$
$\{1,3,v\}$	$\widetilde{K}_{5,r_1}$	$(3,10), (4,7)$	$6$
$\{2,4,v\}$	$\widetilde{K}_{5,r_1}$	$(3,10), (4,9), (v,5)$	$8$
$\{1,2,3,4\}$	Prism	$(4,9)$	$4, 6, 7$
$\{1,2,3,v\}$	Prism	$(2,9), (v,8)$	$5, 6, 7$
$\{1,2,4,v\}$	Prism	$(4,8)$	$5, 7, 9$

Note that all extensions of $\widetilde{K}_{5,r_3}$ have either an $M^*(K_5\backslash e)$-minor, or a $\widetilde{K}_{5,r_1}$-minor. So the next lemma follows easily from Lemma 3.6 and the Strong Splitter Theorem.

Lemma 3.8

Let $M$ be a matroid with a $\widetilde{K}_{5,r_3}$-minor. If $M$ has no $M^*(K_5\backslash e)$-minor, then $M$ has rank $5$.

Finally we study matroids that have a minor isomorphic to $\widetilde{K}_{5,r_4}$. We will list all single-element extensions of $\widetilde{K}_{5,r_4}$. See Fig. 5 for a fundamental graph of $\widetilde{K}_{5,r_4}$. Note that the symmetries between $1$ and $3$, and between $2$ and $4$. So there are eleven cases.

$neigh(u)$	Minor?	Pivots	Deletion
$\{1,2\}$	$\widetilde{K}_{5,r_1}$	$(2,u), (3,6)$	$7$
$\{1,3\}$	$\widetilde{K}_{5,r_1}$	$(3,u), (4,7)$	$6$
$\{1,v\}$	$\widetilde{K}_{5,r_1}$	$(1,u)$	$1$
$\{2,v\}$	$\widetilde{K}_{5,r_1}$	$(4,9), (v,u)$	$4$
$\{2,4\}$	$\widetilde{K}_{5,r_1}$	$(3,9), (4,u), (v,5)$	$6$
$\{1,2,3\}$	$None; \cong \widetilde{K}_{5,r_4,c_1}$
$\{1,2,4\}$	$None; \cong \widetilde{K}_{5,r_4,c_1}$
$\{2,4,v\}$	$None; \, \widetilde{K}_{5,r_4,c_1}$
$\{1,2,3,4\}$	$\widetilde{K}_{5,r_1}$	$(1,8), (2,5), (3,u)$	$3$
$\{1,2,3,v\}$	$\widetilde{K}_{5,r_1}$	$(1,u)$	$1$
$\{1,2,4,v\}$	$\widetilde{K}_{5,r_1}$	$(1,u)$	$1$

Lemma 3.9

Let $M$ be a matroid with a $\widetilde{K}_{5,r_4}$-minor. If $M$ has no $M^*(K_5\backslash e)$-minor, then $M$ has rank $5$.

Proof

It follows from Lemmas 3.6 , 3.5, and the Strong Splitter Theorem that we need to study only one extension of $\widetilde{K}_{5,r_4}$, namely $\widetilde{K}_{5,r_4,c_1}$ as shown in the table above.

First we look at matroids obtained from $\widetilde{K}_{5,r_4}$ by an extension and then a coextension. Let $u$ be the extension element and let $w$ be the coextension element. By symmetry, we have the following cases.

$neigh(u)$	$neigh(w)$	Prism Minor?	Pivots	Deletions	Contraction
$\{2,4,v\}$	$\{5,u\}$	Yes	$(1,9)$	$1, 6, 8$	$4$
$\{2,4,v\}$	$\{9,u\}$	Yes	$(w,u)$	$6, 8, 10$	$v$
$\{2,4,v\}$	$\{10,u\}$	Yes	$(v,8)$	$v, 6, 9$	$8$
$\{2,4,v\}$	$\{5,8,9,10,u\}$	Yes	$(w,8)$	$5, 7, 9$	$8$
$\{2,4,v\}$	$\{5,6,9\}$	Yes	$(w,6)$	$5, 7, 8$	$v$
$\{2,4,v\}$	$\{5,6,7,8,9,10\}$	Yes	$(w,10)$	$6, 8, 9$	$10$

Next we look at matroids obtained from $\widetilde{K}_{5,r_4}$ by two extensions and then completing the triad. Let $u$ and $w$ be the two extension elements and let $x$ the the coextension element. By symmetry, we may assume that $neigh(u) = \{2,4,v\}$, $neigh(w)=\{1,2,3\}$, and $neigh(x)=\{u,w\}$. It is easy to check that this matroid has an $M^*(K_5 \backslash e)$-minor; one may pivot on $(4,8)$ and $(w,x)$, contract 3, and then delete $5$, $7$, $9$, and $10$.