Principal component selection via adaptive regularization method and generalized information criterion

Abstract

The principal component analysis has been widely used in various fields of research (e.g., bioinformatics, medical statistics, etc.), especially high dimensional data analysis. Although crucial components selection is a vital matter in principal components analysis, relatively little attention was paid to this issue. The existing studies for principal component analysis were based on ad-hoc methods (e.g., method with cumulative percent variance or average eigenvalue). We propose a novel method for selecting principal component based on L$_{1}$-type regularized regression modeling. In order to effectively perform for principal component regression, we consider adaptive L$_{1}$-type penalty based on singular values of components, and propose adaptive penalized principal component regression. The proposed method can perform feature selection incorporating explanation power of components for not only high-dimensional predictor variables but also response variable. In sparse regression modeling, choosing the regularization parameter is a crucial issue, since feature selection and estimation heavily depend on the selected regularization parameter. We derive a model selection criterion for choosing the regularization parameter of the proposed adaptive L$_{1}$-type regularization method in line with a generalized information criterion. Monte Carlo simulations and real data analysis demonstrate that the proposed modeling strategies outperform for principal component regression modeling.

1 Introduction

The principal component analysis (PCA) has drawn a large amount of attention for high-dimensional data analysis (e.g., genomic data, social network profiles data, etc.). Especially, the principal component regression has been widely used to overcome multicollinearity and drawbacks of small samples with large number of features problem (Chang and Yang 2012). The crucial issue in PCA is a selection of principal components, since researches though PCA begin with interpretation of the selected components. Although various methods, such as average eigenvalue (AE) (Valle et al. 1999), Cumulative Percent Variance (CPV) method (Valle et al. 1999), etc., were proposed and have been used in various fields of research, the methods are ad-hoc.

We consider crucial components selection via principal component regression (PCR) based on an adaptive L$_{1}$-type regularization method. The adaptive L$_{1}$-type regularization methods [e.g., adaptive lasso (Zou 2006), adaptive elastic net (Zou and Hastie 2008)] can effectively perform for feature selection and model estimation simultaneously by discriminately imposing a weighted L$_{1}$-type penalty. Relatively little attention, however, was paid to the use of L$_{1}$-type regularization method to principal components analysis, even though component selection is also crucial in PCA.

We propose a novel method for principal component regression in line with the adaptive L$_{1}$-type regularization. In principal components analysis, singular values indicate significance of each component for explaining the dataset. We incorporate the explanation power of components into regression modeling procedures by imposing an adaptive L$_{1}$-type penalty based on the singular values, and propose an adaptive penalized principal component regression (APPCR). In APPCR, components capturing large proportion of variance in data receive relatively a small amount of penalties, and thus regression coefficients of the components may be estimated in large. On the other hand, components corresponding small singular values receive a large amount of penalties, and thus their coefficients are estimated in small or deleted in the model. It implies that the proposed APPCR effectively performs for feature selection and principal component regression modeling by incorporate significance of components for explaining not only high-dimensional predictor variables but also response variable.

A vital matter in L$_{1}$-type regularization method is choosing the regularization parameter, since the parameter selection can be seen as model selection and evaluation. Although the cross validation (CV) and traditional criteria [e.g., AIC (Akaike 1973) and BIC (Schwarz 1978)] have been widely used to select regularization parameter (Yang et al. 2014; Xu et al. 2014), the CV suffers from instability and overfitting in sparse regression modeling (Wang et al. 2007). Furthermore, the traditional criteria are not suitable for sparse regression modeling, since the criteria were derived based on assumption that model is estimated by maximum likelihood method (Konishi and Kitagawa 1996). We derive an information criterion for choosing the regularization parameter in line with the generalized information criterion, which was proposed for evaluating model estimated by various statistical methods, not only maximum likelihood method (Konishi and Kitagawa 1996; Park et al. 2012).

The rest of this paper is organized as follows. In Sect. 2, we introduce the proposed adaptive penalized principal component regression. Section 3 presents the derived information criterion for choosing the regularization parameter. In Sect. 4, Monte Carlo experiments are conducted to examine the effectiveness of the proposed modeling strategies. The real world example based on NCI60 dataset is shown in Sect. 5. Some concluding remarks are given in Sect. 6.

2 Adaptive penalized principal component regression

Suppose we have n independent observations $\{(y_{i},\varvec{x}_{i}); i=1,\ldots ,n\}$, where $y_{i}$ are random response variables and $\varvec{x}_{i}$ are p-dimensional vectors of the predictor variables. Consider the linear regression model,

$$\begin{aligned} y_{i}=\varvec{x}^{T}_{i}\varvec{\beta }+\varepsilon _{i}, \quad i=1,\ldots ,n, \end{aligned}$$

(1)

where $\varvec{\beta }$ is an unknown p-dimensional vector of regression coefficients and $\varepsilon _{i}$ are the random errors which are assumed to be independently, identically distributed with mean 0 and variance $\sigma ^{2}$. We consider a high dimensional data situation ($p\gg n$).

The most widely used and fundamental method for extracting information and dimension reduction in high-dimensional data analysis is PCA. In this study, we consider principal component selection vie principal component regression modeling based on L$_{1}$-type regularization.

2.1 Principal component regression

The singular value decomposition (SVD) is preceded for principal component analysis. The SVD of predictor variables $\varvec{X}$ is given as

$$\begin{aligned} \varvec{X}={\mathbf {USV}}^{T}, \end{aligned}$$

(2)

where $\varvec{S}=\mathrm {diag}(\lambda _{1},\lambda _{2},\ldots ,\lambda _{q})$ is a $q\times q$ diagonal matrix with non-zero singular values [i.e., q=rank($\varvec{X}$)]. The columns of $\varvec{U}$ and $\varvec{V}$ are orthogonal, which are left and right singular vectors of S, respectively.

The principal components analysis is based on covariance matrix $\varvec{X}^{T}\varvec{X}$. The eigen-decomposition of $\varvec{X}^{T}\varvec{X}$ is given as

$$\begin{aligned} \varvec{X}^{T}\varvec{X}= & {} ({\mathbf {USV}}^{T})^{T}({\mathbf {USV}}^{T})\nonumber \\= & {} {\mathbf {VSU}}^{T}{\mathbf {USV}}^{T}\nonumber \\= & {} {\mathbf {VS}}^{2}\varvec{V}^{T}, \end{aligned}$$

(3)

where $S^{2}$ is diagonal matrix with eigenvalues $(\lambda ^{2}_{1}\ge \lambda ^{2}_{2}\ge \cdots \ge \lambda ^{2}_{q})$, and columns of $\varvec{V}$ denote the corresponding orthogonal set of eigenvectors. Then, $\varvec{v}_{k}$ is principal component direction corresponding to the $k^{th}$ largest eigenvalue $\lambda ^{2}_{k}$, and corresponding principal component is given as

$$\begin{aligned} \varvec{z}_{k}=\varvec{X}\varvec{v}_{k},\quad k=1,\ldots ,q. \end{aligned}$$

(4)

The regression model based on the principal components is constructed by

$$\begin{aligned} y_{i}=\varvec{z}^{T}_{i}\varvec{\eta }+\varepsilon _{i},\quad i=1,\ldots ,n, \end{aligned}$$

(5)

where $\varvec{\eta }$ is an unknown q-dimensional vector of regression coefficients.

The PCA is usually based on not all the components but some of the components having crucial information to explain the dataset $\varvec{X}$. In other words, identifying crucial principal components and dimension reduction based on the identified components are crucial issues in PCA. Although the issue is a vital matter in PCA, relatively little attention was paid to the issue, and existing studies were based on the following ad-hoc methods (Valle et al. 1999),

• Average eigenvalue (AE): The method is based on components corresponding eigenvalues greater than average of eigenvalues of all components.

• Cumulative percent variance (CPV): The method is based on d components capturing the m % variance (e.g., $m=75, 85, 90$, or 95).

• Methods based on eigenvalue without criterion.

2.2 Adaptive penalized principal component regression

We propose a novel methodology for crucial component selection via principal component regression modeling based on an adaptive L$_{1}$-type regularization method. In recent year, L$_{1}$-type regularization has drawn a large amount of attention for regression modeling (Qingguo 2014; Neykov et al. 2014). By imposing the L$_{1}$-type penalty, the method can perform estimation and feature selection simultaneously. Furthermore, various adaptive L$_{1}$-type regularization methods with one’s purpose were also proposed to improve feature selection accuracy (Zou 2006; Zou and Hastie 2008; Park and Sakaori 2013; Hirose and Konishi 2012). The adaptive L$_{1}$-type regularization methods (e.g., adaptive lasso, adaptive elastic net and etc.) impose discriminate penalties to each feature depending on their significance as follows,

• Adaptive lasso

  $$\begin{aligned} \hat{\varvec{\beta }}^{adLasso}=\mathop {\mathrm{arg min}}\limits _{\varvec{\beta }}\left\{ \frac{1}{2}\sum ^{n}_{i=1}\left( y_{i}-\varvec{x}^{T}_{i}\varvec{\beta }\right) ^{2}+\gamma \sum ^{p}_{j=1}\hat{w}_{j}\left| \beta _{j}\right| \right\} , \end{aligned}$$

  (6)

• Adaptive elastic net

  $$\begin{aligned} \hat{\varvec{\beta }}^{adEla}=\mathop {\mathrm{arg min}}\limits _{\varvec{\beta }}\left\{ \frac{1}{2}\sum ^{n}_{i=1}\left( y_{i}-\varvec{x}^{T}_{i}\varvec{\beta }\right) ^{2}+\gamma _{1}\sum ^{p}_{j=1}\hat{w}_{j}\left| \beta _{j}\right| +\gamma _{2}\sum ^{p}_{j=1}\beta ^{2}_{j}\right\} , \end{aligned}$$

  (7)

  where $\hat{w}=1/|\hat{\beta }_{j}|^\nu$, $\nu >0$ and the least square estimators or the ridge estimators can be used as $\hat{\varvec{\beta }}$.

We consider an adaptive L$_{1}$-type regularization for principal components selection. In PCA, singular values indicates explanation power of components for explaining $\varvec{X}$. It implies that the component corresponding a large singular value is a crucial feature to explain high-dimensional data $\varvec{X}$ (i.e., a crucial feature to capture directions of maximal variance in dataset).

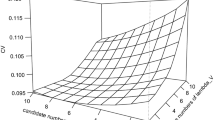
Figure 1 shows averages of absolute values of least square estimators $\hat{\varvec{\eta }}^{LS}$ in (5) and singular values of principal components from $\varvec{X}$, which are from regression models with $p=10$ and $n=100$ in 100 replicated datasets. We can see through Fig. 1 that the results of least squares estimator and singular values show similar patterns about importance of principal components, even though $\hat{\varvec{\eta }}^{LS}$ is obtained from regression ${\mathbf {Z}}$ on $\varvec{y}$, and the singular values are obtained from only $\varvec{X}$. It means that we can perform effectively principal component selection through the method based on singular value as incorporating significance of components for explaining $\varvec{X}$ and $\varvec{y}$. It implies that components capturing direction of maximal variance can be easily selected by a method based on singular values.

Fig. 1

Absolute least square estimators and Singular values of principal components

In order to incorporate the fundamental idea of PCA into regression modeling, we consider a weight based on singular values, and propose an APPCR,

$$\begin{aligned} \hat{\varvec{\eta }}=\mathop {\mathrm{arg min}}\limits _{\beta }\left\{ \frac{1}{2}\sum ^{n}_{i=1}\left( y_{i}-\varvec{z}^{T}_{i}\varvec{\eta }\right) ^{2}+\gamma \sum _{k=1}^{q}w^{pca}_{k}\left| \eta _{k}\right| \right\} , \end{aligned}$$

(8)

where $\gamma$ is a tuning parameter controlling model complexity and

$$\begin{aligned} w^{pca}_{k}=\sqrt{\frac{1}{\lambda _{k}/ \text {max}(\mathrm {d}\varvec{S})}}, \end{aligned}$$

(9)

where d$\varvec{S}$ is diagonal elements of matrix $\varvec{S}$. The proposed $w^{pca}_{k}$ reflects relative significance of principal component to explain $\varvec{X}$, and the components corresponding small singular value receive relatively large penalties in APPCR. Thus, coefficients of the components are estimated in small or to exactly zero in the propose method. In short, the proposed APPCR can perform feature selection for not only predicting response variable and but also explaining predictor variables dataset by impose the adaptive penalty based on singular value. It implies that our method incorporates the properties of PCA (i.e., significance principal components to explain high-dimensional dataset $\varvec{X}$) to regression modeling based on the weight.

3 Regularization parameter selection via information theoretic viewpoint

In the proposed APPCR, choosing the regularization parameter $\gamma$ is a crucial issue, because component selection and model estimation heavily rely on the selected regularization parameter. The regularization parameter in L$_{1}$-type regularization methods has been usually selected by using CV or traditional information criteria (e.g., AIC and BIC). However, it is well known that the CV leads to time consuming, and provides unstable and overfitting modeling results (Wang et al. 2007). Furthermore, the traditional criteria are not suitable to APPCR, since the criteria were derived under the assumption that model is estimated by maximum likelihood method (Konishi and Kitagawa 1996, 2008).

We consider a generalized information criterion (GIC), proposed by Konishi and Kitagawa (1996), for regularization parameter selection. The GIC was derived by relaxing the following assumptions imposed on the AIC: model is estimated by maximum likelihood method, and it carried out in a parametric family of distributions including the true model. To derive the GIC, Konishi and Kitagawa (1996, 2008) considered an empirical distribution function $\hat{G}(y)$ based on n observations and employed a q-dimensional functional estimator, $\hat{\varvec{\theta }}=\mathbf {T}(\hat{G})$, which is second order compact differentiable at G. Then, they finally derived GIC for evaluating the model with functional estimator $\hat{\varvec{\theta }}=\mathbf {T}(\hat{G})$ (Konishi and Kitagawa 1996, 2008).

We derive a model evaluation criterion to select regularization parameter of APPCR in line with the GIC (Konishi and Kitagawa 1996; Park et al. 2012). In derivative of information criteria, a bias correction term is crucial,

$$\begin{aligned} \text {tr}\left\{ \int {\mathbf {T}}^{(1)}(G)\frac{\partial \text {log} f(y|{\mathbf {z}},\varvec{\eta })}{\partial \varvec{\eta }^{T}} \right\} , \end{aligned}$$

(10)

where ${\mathbf {T}}^{(1)}(G)$ is an influence function, which plays a key role in derivative of GIC, and $f(y|{\mathbf {z}},\hat{\varvec{\eta }})$ is an estimated model by the proposed APPCR. We suppose that $f(y|{\mathbf {z}},\hat{\varvec{\eta }})$ is based on data drawn from the distribution $G({\mathbf {z}})$ under the assumption that $\varepsilon _{i}$ in (5) are the random errors from $N(0,\sigma ^{2})$, and consider the following linear regression model,

$$\begin{aligned} f(y_{i}|{\mathbf {z}}_{i},\varvec{\eta })=\frac{1}{\sqrt{2\pi \sigma ^{2}}}\text {exp}\left[ -\frac{\{y_{i}-{\mathbf {z}}^{T}_{i}\varvec{\eta }\}^{2}}{2\sigma ^{2}} \right] , \end{aligned}$$

(11)

where ${\varvec{\eta }}$ is a q-dimensional estimator defined as the solution of the system of implicit equation,

$$\begin{aligned} \frac{\partial }{\partial \varvec{\eta }}\left\{ \frac{1}{2}\sum ^{n}_{i=1}\left( y_{i}-\varvec{z}^{T}_{i}\varvec{\eta }\right) ^{2}+\gamma \sum _{k=1}^{q}w^{pca}_{k}\left| \eta _{k}\right| \right\} . \end{aligned}$$

(12)

However, the L$_{1}$ penalty $P^{w}_{\gamma }(|\varvec{\eta }|)=\gamma \sum _{k=1}^{q}w^{pca}_{k}|\eta _{k}|$ in (12) is not differentiable, and thus information criterion for APPCR cannot be derived. To settle on the issue, we refer to local quadratic approximation (LQA) as following (Fan and Li 2001; Park et al. 2012),

$$\begin{aligned} \left[ P^{w}_{\gamma }(|{\eta }_{k}|)\right] '= & {} \gamma \left[ P'^{w}(|{\eta }_{k}|)\text {sign}(\eta _{k})\right] \nonumber \\\approx & {} \gamma \left[ \{P'^{w}(\left| {\eta }_{k0}|\right) /|\eta _{k0}|\}\eta _{k}\right] \nonumber \\= & {} \gamma \left\{ \left( w^{pca}_{k}/|\eta _{k0}|\right) \eta _{k}\right\} . \end{aligned}$$

(13)

By using LQA, the (12) is given as,

$$\begin{aligned} -\sum ^{n}_{i=1}(y_{i}-\varvec{z}^{T}_{i}\varvec{\eta })\varvec{z}^{T}_{i}+\gamma \left\{ \left( w^{pca}_{k}/|\eta _{k0}|\right) \eta _{k}\right\} . \end{aligned}$$

(14)

It implies that the estimator $\hat{\varvec{\eta }}$ is given by $\hat{\varvec{\eta }}={\mathbf {T}}(\hat{G})$ for q-dimensional functional vector ${\mathbf {T}}(G)$, which is defined as the solution of the implicit equations,

$$\begin{aligned} \approx \int \left[ (y-{\mathbf {z}}^{T}{\mathbf {T}}(G)){\mathbf {z}}-\gamma \{({\mathbf {w}}^{pca}/|{\mathbf {T}}_{0}|){\mathbf {T}}(G)\}\right] \mathrm {d}G(y)={\mathbf {0}}. \end{aligned}$$

(15)

To derive the influence function ${\mathbf {T}}^{(1)}(G)$, G is substituted with $(1-\varepsilon )G+\varepsilon \delta _{y}$ as follows,

$$\begin{aligned}&\int \left[ (y-{\mathbf {z}}^{T}{\mathbf {T}}((1-\varepsilon )G+\varepsilon \delta _{y})){\mathbf {z}}-\gamma ({\mathbf {w}}^{pca}/|{\mathbf {T}}_{0}|){\mathbf {T}}((1-\varepsilon )G+\varepsilon \delta _{y})\right] \nonumber \\&\quad \mathrm {d}((1-\varepsilon )G(y)+\varepsilon \delta _{y})={\mathbf {0}}. \end{aligned}$$

(16)

We then differentiate both sides of the equation with respect to $\varepsilon$ as follows,

$$\begin{aligned}&\int \left[ -{\mathbf {z}}{\mathbf {z}}^{T}\frac{\partial }{\partial \varepsilon }{\mathbf {T}}[(1-\varepsilon )G+\varepsilon \delta _{y}]\!-\!\gamma ({\mathbf {w}}^{pca}/|{\mathbf {T}}_{0}|)\frac{\partial }{\partial \varepsilon }{\mathbf {T}}[(1-\epsilon )G+\epsilon \delta _{y}]\right] \nonumber \\&\quad \times \,\mathrm{d}((1-\varepsilon )G(y)+\varepsilon \delta _{y})\nonumber \\&\quad +\int \left[ (y-{\mathbf {z}}^{T}{\mathbf {T}}[(1-\varepsilon )G+\varepsilon \delta _{y}]){\mathbf {z}}-\gamma \{({\mathbf {w}}^{pca}/|{\mathbf {T}}_{0}|){\mathbf {T}}[(1-\varepsilon )G+\varepsilon \delta _{y}]\}\right] \nonumber \\&\quad \times \,\mathrm{d}(\delta _{y}-G(y)),={\mathbf {0}}, \end{aligned}$$

(17)

and set $\varepsilon =0$, then we have

$$\begin{aligned}&\int \left\{ -{\mathbf {z}}{\mathbf {z}}^{T}-\gamma \left( {\mathbf {w}}^{pca}/|{\mathbf {T}}_{0}|\right) \right\} \mathrm {d}G(y)\cdot \frac{\partial }{\partial \varepsilon }{\mathbf {T}}\left[ \left( 1-\varepsilon \right) G+\varepsilon \delta _{y}\right] \end{aligned}$$

(18)

$$\begin{aligned}&+\int \left[ \left( y-{\mathbf {z}}^{T}{\mathbf {T}}(G)\right) {\mathbf {z}}-\gamma \left\{ \left( {\mathbf {w}}^{pca}/|{\mathbf {T}}_{0}|\right) {\mathbf {T}}(G)\right\} \right] \mathrm {d}\delta _{y}\end{aligned}$$

(19)

$$\begin{aligned}&-\int \left[ \left( y-{\mathbf {z}}^{T}{\mathbf {T}}(G)\right) {\mathbf {z}}-\gamma \left\{ \left( {\mathbf {w}}^{pca}/|{\mathbf {T}}_{0}\right| ){\mathbf {T}}(G)\right\} \right] \mathrm {d}G(y)\\&={\mathbf {0}}.\nonumber \end{aligned}$$

(20)

The equation (19) is given as,

$$\begin{aligned}&\int \left[ \left( y-{\mathbf {z}}^{T}{\mathbf {T}}(G)\right) {\mathbf {z}}-\gamma \left\{ \left( {\mathbf {w}}^{pca}/|{\mathbf {T}}_{0}|\right) {\mathbf {T}}(G)\right\} \right] \mathrm {d}\delta _{y}\\&\quad =\left[ \left( y-{\mathbf {z}}^{T}{\mathbf {T}}(G)\right) {\mathbf {z}}-\gamma \left\{ \left( {\mathbf {w}}^{pca}/|{\mathbf {T}}_{0}|\right) {\mathbf {T}}(G)\right\} \right] ,\nonumber \end{aligned}$$

(21)

and, the equation (20) equals ${\mathbf {0}}$ given as (15).

Consequently, the influence function, ${\mathbf {T}}^{(1)}(G)$, of the functional that defines the APPCR estimator is given by

$$\begin{aligned}&{\mathbf {T}}^{(1)}(G)\equiv \frac{\partial }{\partial \varepsilon }{\mathbf {T}}((1-\varepsilon )G+\varepsilon \delta _{y})\Big |_{\varepsilon =0}\nonumber \\&\quad =\left\{ \int {\mathbf {z}}{\mathbf {z}}^{T}\!+\!\gamma ({\mathbf {w}}^{pca}/|{\mathbf {T}}_{0}|) \mathrm {d}G(y)\right\} ^{-1}\!\left[ (y\!-\!{\mathbf {z}}^{T}{\mathbf {T}}(G)){\mathbf {z}}\!-\!\gamma \left\{ ({\mathbf {w}}^{pca}/|{\mathbf {T}}_{0}|){\mathbf {T}}(G)\right\} \right] .\nonumber \\ \end{aligned}$$

(22)

Thus, the a bias correction term (10) in generalized information criterion is given by

$$\begin{aligned}&b^{(1)}=\text {tr}\left( \left[ \int {\mathbf {z}} {\mathbf {z}}^{T}+\gamma ({\mathbf {w}}^{pca}/|{\mathbf {T}}_{0}|)\mathrm {d}G(y) \right] ^{-1}\right. \nonumber \\&\quad \times \left. \left[ \int \left[ (y\!-\!{\mathbf {z}}^{T}{\mathbf {T}}(G)){\mathbf {z}}-\gamma \left\{ ({\mathbf {w}}^{pca}/|{\mathbf {T}}_{0}|){\mathbf {T}}(G)\right\} \right] \!\cdot \frac{\partial \text {log} f(y|{\mathbf {z}},\varvec{\eta })}{\partial \varvec{\eta }^{T}}\Big |_{\varvec{\eta }\!=\!{\mathbf {T}}(G)}\mathrm {d}G(y)\!\right] \right) \nonumber \\&\quad +\,O(n^{-1}). \end{aligned}$$

(23)

By replacing the unknown distribution G by the empirical distribution $\hat{G}$, and subtracting the asymptotic bias estimate from the log-likelihood, we have an information criterion for the statistical model $f(y|{\mathbf {z}},\hat{\varvec{\eta }}(\gamma ))$ with the functional estimator, $\hat{\varvec{\eta }}(\gamma )={\mathbf {T}}(\hat{G})$, as following

$$\begin{aligned} \textit{GIC}_{\textit{APPCR}}=-2\sum ^{n}_{i=1}\text {log} f(y_{i}|{\mathbf {z}}_{i},\hat{\varvec{\eta }}(\gamma ))+2\left\{ R(\hat{G})^{-1}Q(\hat{G})\right\} , \end{aligned}$$

(24)

where

$$\begin{aligned} R(\hat{G}= & {} \int {\mathbf {z}}{\mathbf {z}}^{T}+\gamma ({\mathbf {w}}^{pca}/|{\mathbf {T}}_{0}|)dG(y),\\= & {} \frac{1}{n}\left\{ Z^{T}Z+\Sigma _{\gamma }(\varvec{\hat{\eta }})\right\} , \end{aligned}$$

(25)

$$\begin{aligned} Q(\hat{G})= & {} \int \left[ \left( y-\!{\mathbf {z}}^{T}{\mathbf {T}}(\hat{G})\right) {\mathbf {z}}\!-\!\gamma \left\{ ({\mathbf {w}}^{pca}/|{\mathbf {T}}_{0}|){\mathbf {T}}(\hat{G})\right\} \right] \!\cdot \frac{\partial \text {log} f(y|{\mathbf {z}},\varvec{\eta })}{\partial \varvec{\eta }^{T}}\Big |_{\varvec{\eta }\!=\!{\mathbf {T}}(\hat{G})}\mathrm {d}G(y)\nonumber \\= & {} \frac{1}{n\sigma ^{2}}\left\{ Z^{T}{\hat{\Lambda }}^{2}Z-\Sigma _{\gamma }(\hat{\varvec{\eta }}){\hat{\varvec{\eta }}}\varvec{1}^{T}_{n}{\hat{\Lambda }}Z\right\} , \end{aligned}$$

(26)

where $\hat{\Lambda }$ and $\Sigma _{\gamma }(\varvec{\hat{\eta }})$ are $n \times n$ and $q \times q$ diagonal matrices, respectively,

$$\begin{aligned}&\hat{\Lambda }=\text {diag}\left\{ (y_{1}-\varvec{z}^{T}_{1}\hat{\varvec{\eta }}),(y_{2}-\varvec{z}^{T}_{2}\hat{\varvec{\eta }}),\ldots ,(y_{1}-\varvec{z}^{T}_{n}\hat{\varvec{\eta }})\right\} ,\end{aligned}$$

(27)

$$\begin{aligned}&\Sigma _{\gamma }(\hat{\varvec{\eta }})=\gamma \text {diag}\left\{ w^{pca}_{1}/|\eta _{1,0}|,w^{pca}_{2}/|\eta _{2,0}|,\ldots ,w^{pca}_{q}/|\eta _{q,0}|\right\} , \end{aligned}$$

(28)

and $\varvec{1}_{n}=(1,1,\ldots ,1)^{T}$ is an n-dimensional vector.

The proposed APPCR is based on selected tuning parameter $\gamma ^{*}$ minimizing the derived $GIC_{APPCR}$.

4 Monte Carlo experiments

We conduct Monte Carlo experiments to show the effectiveness of the proposed modeling strategies. We simulate 100 datasets from the linear regression model

$$\begin{aligned} y_{i}=\varvec{x}^{T}_{i}\varvec{\beta }+\sigma \varepsilon _{i},\quad i=1,\ldots ,n, \end{aligned}$$

(29)

where $\varepsilon _{i}$ are standard normal, and the correlation between $x_{l}$ and $x_{m}$ is $\rho ^{|l-m|}$. We consider sample size $n=100$, and number of predictor variables $p=100, 1000$ with $\beta _{j}=1$ for randomly selected 50 % of features $\varvec{x}_{j}$ and $\beta _{j}=0$ for other 50 % of features $\varvec{x}_{j}$. The correlation $\rho =0.25, 0.5, 0.75$ and $\sigma =1, 3$ are considered in linear regression model. We first perform PCA for the predictor variables $\varvec{X}$, and then apply the proposed modeling strategies to principal component regression modeling.

Table 1 Comparison of GIC$_{APPCR}$ with CV

We first evaluate the derived $\textit{GIC}_{\textit{APPCR}}$ as a regularization parameter selector by compare with CV. Table 1 shows root mean square error (RMSE) and its standard deviation based on the proposed APPCR, where the bold numbers indicate better performance between the CV and GIC. We can see through Table 1 that the derived $\textit{GIC}_{\textit{APPCR}}$ shows outstanding performances for predict accuracy compared with the cross validation. Furthermore, it can be seen that CV shows unstable results as shown in columns “STD.RMSE”, especially in high dimensional data situations (i.e., $p\gg n$). It implies that the $\textit{GIC}_{\textit{APPCR}}$ is a useful tool for regularization parameter selection for principal component regression in the viewpoint of prediction accuracy and stability.

We also evaluate the performance of the proposed adaptive penalized principal component regression compared the existing methods: “AE”, “CPV ($m=85~\%$)” and “ordinary Lasso”. Because we confirmed the superiority of the GIC to the CV in Table 1, we will compare the performances of APPCR and existing methods based on the GIC. Tables 2 and 3 show the RMSE and its standard deviation for $p=100$ and 1000, respectively, where the bold numbers indicate the best performance among the AE, CPV, Lasso and APPCR. We can see through Tables 2 and 3 that the proposed APPCR shows outstanding performances for principal component regression in overall. It can be also seen that L$_{1}$-type regularization methods (i.e., APPCR and Lasso) provide stable modeling results compared with PCR based on AE and CPV in high dimensional situation. Especially, the proposed APPCR shows stable results as shown in columns “STD.RMSE” of Tables 2 and 3. It implies that the proposed weight based on singular value performs properly principal component selection, and it leads to outstanding performance for principal component regression.

Table 2 Simulation results with $p=100$

Table 3 Simulation results with $p=1000$

5 Real example

We apply the proposed modeling strategies (i.e., APPCR and GIC$_{APPCR}$) to the cancer cell panel of the National Cancer Institute, called a NCI60 dataset, which is benchmarking of Alfons et al. (2013). The dataset consists of 60 human cancer cell lines and expression levels of 44,882 genes (http://discover.nci.nih.gov/cellminer/). We consider 24,234 genes by delete genes with vague symbols (e.g., “-”). We also consider transformed protein expressions based on 162 antibodies via reverse-phase protein lysate array. We delete one cell line with missing values in expression levels of all genes. Thus, we consider the 24,234 gene expression levels in 59 cell lines as predictor variables in linear regression model, and protein expression levels of each antibody as a response variable.

We consider the protein expressions of 10 antibodies with the highest variation for 59 cell lines (i.e., KRT18, KRT19, KRT7, MAP2K2, TP53, GSTP1, CDKN2A, KRT8, GSTP1 and VASP). In other words, we evaluate the proposed APPCR compared with AE, CPV, and Lasso based on 10 regression models. The regularization parameters of lasso and APPCR are selected by the GIC and CV. Figure 2 shows means square error (MSE) in 10 regression models (i.e., APPCR with GIC and CV: AP.G and AP.C, respectively, and lasso with GIC and CV: La.G and La.C, respectively).

Fig. 2

Prediction accuracy in NCI60 data analysis

As shown in Fig. 2, the proposed APPCR based on GIC shows outstanding performances compared with other methods in overall. However, the APPCR based on CV shows poor results in some regression models. It implies that not only modeling strategy but also model evaluation criterion is crucial for regression modeling. In sort, our modeling strategies based on APPCR with GIC$_{APPCR}$ is an effective tool for principal components regression.

There is currently much discussion about high-dimensional genomic data analysis, and extracting information from the dataset has become crucial. We can expect that the proposed modeling strategies will be a vital tool for various fields of research based on high-dimensional dataset.

6 Conclusion and remarks

We have introduced novel modeling strategies for principal component regression based on adaptive L$_{1}$-type regularization. In order to incorporate the fundamental idea of PCA, we have proposed a weight based on singular value of each principal component and use the weight in the adaptive penalty. By using the proposed adaptive L$_{1}$-type penalty, we can perform crucial feature selection in the viewpoint of not only explaining high-dimensional predictor variables, but also predicting response variable. Furthermore, we have derived an information criterion for choosing the regularization parameter of the proposed adaptive penalized principal component regression in line with the generalized information criterion.

In order to evaluate the proposed modeling strategies, we have conducted Monte Carlo simulations and NCI60 data analysis, and compare performances of our methods with existing ones. We have observed through the results that the proposed modeling strategies, i.e., APPCR and GIC$_{\textit{APPCR}}$, outperform for principal component regression in the viewpoint of prediction accuracy and stability.

In this study, we have considered principal component regression based on adaptive L$_{1}$-type regularization method. It is, however, well known that the PCA suffers from interpretation problem about the identified crucial principal components. Further work remains to be done towards conducting principal component regression modeling with variable selection based on information from PCA results (e.g., loading matrix in SVD). Furthermore, our modeling strategies can be extended to high-dimensional data analysis (e.g., genomic dataset analysis) for the purpose of extracting and summarizing crucial information.