Abstract
In a spatial model with Euclidean preferences, we establish that the geometric median satisfies Maskin monotonicity, anonymity, and neutrality. For three agents, it is the unique such rule.



Similar content being viewed by others
Notes
Since \(X=\mathbb {R}^d\), isometries are bijections that correspond to reflections, rotations, and translations.
The geometric median has a rich history in this special case and is sometimes referred to as the Fermat-Torricelli point of a triangle.
An interior angle is simply the angle formed by two adjacent sides of the triangle.
A median of a triangle is any of the line segments connecting a vertex to the midpoint of the opposite side of the triangle.
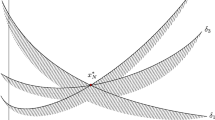
Note that \(c_1'\in con(\triangle _{c_1x_C^*c_2})\) will follow since it is assumed \(\triangle _{c_1'c_2'c_3'}\) has all angles less than or equal to \(120^{\circ }\) while \(\angle _{c_1x_C^*c_2}=120^{\circ }\).
A scalene triangle has all three interior angles of different measure.
Note that as \(c_3\rightarrow c_1\) we have \(\angle _{c_1c_2c_3}\rightarrow 0\) so finding such a \(c_3'\) is always possible by the Intermediate Value Theorem.
This is achieved by moving \(z_2\) and \(z_3\) in tandem towards \(\varphi (Z)\) until each side of the triangle is equal in length.
This follows by the midpoint collinear construction outlined previously.
See Brady and Chambers (2015) for a discussion and result using the dual solution.
References
Baranchuk N, Dybvig PH (2009) Consensus in diverse corporate boards. Rev Fin Stud 22(2):715–747
Barbera S, Peleg B (1990) Strategy-proof voting schemes with continuous preferences. Soc Choice Welf 7(1):31–38
Berga D, Moreno B (2009) Strategic requirements with indifference: single-peaked versus single-plateaued preferences. Soc Choice Welf 32(2):275–298
Black D (1948) On the rationale of group decision-making. J Polit Econ 56(1):23–34
Brady RL, Chambers CP (2015) Spatial implementation. Games Econ Behav 94(2015):200–205
Cervone DP, Dai R, Gnoutcheff D, Lanterman G, Mackenzie A, Morse A, Srivastava N, Zwicker WS (2012) Voting with rubber bands, weights, and strings. Math Soc Sci 64(1):11–27
Chung H, Duggan J (2014) Directional equilibria, working paper
Coxeter H (1989) Introduction to geometry. Wiley, New York
Dasgupta P, Hammond P, Maskin E (1979) The implementation of social choice rules: Some general results on incentive compatibility. Rev Econ Stud 46:185–216
Deimling K (2011) Nonlinear functional analysis. Courier Dover Publications, Mineola
Duggan J (2015) May’s Theorem in one dimension, working paper
Gini C, Galvani L (1929) Di talune estensioni dei concetti di media a caratteri qualitivi. Metron 8:3–209
Güler O (2010) Foundations of optimization, 258th edn. Springer, New York
Haldane J (1948) Note on the median of a multivariate distribution. Biometrika 35(3–4):414–417
Hotelling H (1929) Stability in competition. Econ J 39(153):41–57
Maskin E (1999) Nash equilibrium and welfare optimality. Rev Econ Stud 66(1):23–38
May KO (1952) A set of independent necessary and sufficient conditions for simple majority decision. Econometrica 20(4):680–684
Muller E, Satterthwaite MA (1977) The equivalence of strong positive association and strategy-proofness. J Econ Theory 14(2):412–418
Plott CR (1967) A notion of equilibrium and its possibility under majority rule. Am Econ Rev 57(4):787–806
Author information
Authors and Affiliations
Corresponding author
Additional information
We are grateful to Roy Allen, John Duggan, Bill Zwicker, the guest editor, and two anonymous referees for comments and suggestions. All errors are our own. The result in this manuscript was previously circulated under the title Spatial implementation.
Appendix: Independence of the axioms
Appendix: Independence of the axioms
We now show that the axioms are independent. First, consider the dictatorship social choice rule \(\varphi _d\) such that \(\varphi _d(Z)=z_1\) for all \(Z\in X^N\). It is clear that this rule satisfies neutrality and Maskin monotonicity but violates anonymity.
Next, consider the social choice rule \(\varphi _c\) such that, for each Z in \(X^N\), \(\varphi _c(Z)\) is the unique solution to
The solution to (4) is the mean (or centroid) of the ideal points. Clearly \(\varphi _c\) satisfies anonymity. It is also easy to see that \(\varphi _c\) satisfies neutrality.
However, \(\varphi _c\) does not satisfy Maskin monotonicity. Consider the profile of n agents \(Z=(\text {e}_1,- \text {e}_1,0,\ldots ,0)\) with \(\text {e}_i\) being the ith standard basis vector in \(\mathbb {R}^d\). It follows that \(\varphi _c(Z)=0\). Now \(Z'=(\frac{1}{2}\text {e}_1,- \text {e}_1,0,\ldots ,0)\in MT(Z,\varphi _c(Z))\) by Lemma 3.1 but \(\varphi _c(Z')\ne 0=\varphi _c(Z)\).
Finally consider the social choice rule \(\varphi _m\) such that \(\varphi _m(Z)\) solves
for each \(j\in \{1,\ldots ,d\}\). That is, \(\varphi _m\) selects the coordinate-wise median of the ideal points. It is obvious \(\varphi _m\) satisfies anonymity. It is also fairly easy to see that \(\varphi _m\) satisfies Maskin monotonicity. To see this, simply apply the proof technique used in Lemma 3.2 (see Brady and Chambers 2015) for each coordinate. However, it is a well known fact that the coordinate-wise median does not satisfy neutrality as it is not equivariant with isometries.
Rights and permissions
About this article
Cite this article
Brady, R.L., Chambers, C.P. A spatial analogue of May’s Theorem. Soc Choice Welf 47, 127–139 (2016). https://doi.org/10.1007/s00355-016-0949-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00355-016-0949-0