Private agenda and re-election incentives

Abstract

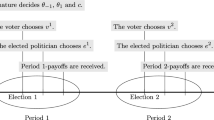
Consider a politician who has to take two sequential decisions during his term in office. For each decision, the politician faces a trade-off between taking what he believes to be the decision that generates a public benefit, thus increasing his chances of re-election, and taking the decision that increases his private gain but is likely to decrease his chances of re-election. In our results we find that if the politician is a good enough decision maker and he desires to be re-elected enough, he takes the action that generates a public benefit regardless of his private interests. Moreover, we find that the behavior such that the politician delays taking the action that generates a public benefit to the last period of his term in office before he is up for re-election is optimal if and only if he has either very high or very low decision making skills.

Appendix: Proofs

Proof of lemma 1

Let $U_E(S)$ be the value of $U_E$ when a certain plan

$$\begin{aligned} S \in \{HH, DD, HD, DH, HC_w, DC_w, HC_r, DC_r\} \end{aligned}$$

is employed. If the politician employs plan HH then it is true that

$$\begin{aligned} U_E(HH)= & {} \frac{1}{2} \left[ \underbrace{\left( \underbrace{\frac{1}{2}}_{{\text {Pr}}(s_1 = 0)} \underbrace{q}_{{\text {Pr}}(\theta _1 = 0|s_1 = 0)} + \underbrace{\frac{1}{2}}_{{\text {Pr}}(s_1 = 1)} \underbrace{(q + \alpha )}_{{\text {Pr}}(\theta _1 = 1|s_1 = 1)}\right) }_{t = 1} \right. \\&\left. +\, \underbrace{\left( \underbrace{\frac{1}{2}}_{{\text {Pr}}(s_2 = 0)} \underbrace{q}_{{\text {Pr}}(\theta _2 = 0|s_2 = 0)} + \underbrace{\frac{1}{2}}_{{\text {Pr}}(s_2 = 1)} \underbrace{(q + \alpha )}_{{\text {Pr}}(\theta _2 = 1|s_2 = 1)}\right) }_{t=2} \right] \\&+ \,\beta \underbrace{q(2-q)}_{{\text {Pr}}(r \ge 1)} U_E(HH). \end{aligned}$$

Which implies

$$\begin{aligned} U_E(HH)= & {} \frac{q + \frac{\alpha }{2}}{1 - q (2-q) \beta }. \end{aligned}$$

Proceeding in a similar fashion, we have that

$$\begin{aligned} U_E(DD)= & {} \frac{\alpha + \frac{1}{2}}{1 - \frac{3}{4} \beta },\\ U_E(HD)= & {} \frac{\frac{1}{2} \left( q + \frac{\alpha }{2}\right) + \frac{1}{2} \left( \alpha + \frac{1}{2}\right) }{1 - \frac{1+q}{2} \beta },\\ U_E(DH)= & {} \frac{\frac{1}{2} \left( q + \frac{\alpha }{2}\right) + \frac{1}{2} \left( \alpha + \frac{1}{2}\right) }{1 - \frac{1+q}{2} \beta }.\\ \end{aligned}$$

If the politician employs plan $HC_w$ then it is true that

$$\begin{aligned} U_E(HC_w)= & {} \frac{1}{2} \left[ \underbrace{\left( \underbrace{\frac{1}{2}}_{{\text {Pr}}(s_1 = 0)} \underbrace{q}_{{\text {Pr}}(\theta _1 = 0|s_1 = 0)} + \underbrace{\frac{1}{2}}_{{\text {Pr}}(s_1 = 1)} \underbrace{(q + \alpha )}_{{\text {Pr}}(\theta _1 = 1|s_1 = 1)}\right) }_{t = 1} \right. \\&+\left. \underbrace{\underbrace{q}_{{\text {Pr}}(\theta _1 = s_1)} \left( \underbrace{\frac{1}{2}}_{{\text {Pr}}(s_2 = 0)} \underbrace{(1-q + \alpha )}_{{\text {Pr}}(\theta _2 = 0| s_2 = 0)} + \underbrace{\frac{1}{2}}_{{\text {Pr}}(s_1 = 1)} \underbrace{(q + \alpha )}_{{\text {Pr}}(\theta _2 = 1| s_2 = 1}\right) + \underbrace{(1-q)}_{{\text {Pr}}(\theta _1 \ne s_1)} \left( \frac{1}{2} \underbrace{q}_{\theta _1 = 0} + \frac{1}{2} \underbrace{(q + \alpha )}_{\theta _1 = 1}\right) }_{t = 2} \right] \\&+\,\beta \underbrace{q(2-q)}_{{\text {Pr}}(r \ge 1)} U_E(HC_w). \end{aligned}$$

Hence, we have the following:

$$\begin{aligned} U_E(HC_w)= & {} \frac{\left( 1-\frac{q}{2}\right) \left( q + \frac{\alpha }{2}\right) + \frac{q}{2} \left( \alpha + \frac{1}{2}\right) }{1 - q (2-q) \beta }. \end{aligned}$$

Thus, proceeding as above

$$\begin{aligned} U_E(DC_w)= & {} \frac{\frac{1}{4} \left( q + \frac{\alpha }{2}\right) + \frac{3}{4} \left( \alpha + \frac{1}{2}\right) }{1 - \frac{1+q}{2} \beta },\\ U_E(HC_r)= & {} \frac{\left( \frac{1}{2}+\frac{q}{2}\right) \left( q + \frac{\alpha }{2}\right) + \left( \frac{1}{2}-\frac{q}{2}\right) \left( \alpha + \frac{1}{2} \right) }{1 - \frac{1+q}{2} \beta },\\ U_E(DC_r)= & {} \frac{\frac{1}{4} \left( q + \frac{\alpha }{2} \right) + \frac{3}{4} \left( \alpha + \frac{1}{2}\right) }{1 - \frac{3}{4} \beta }. \end{aligned}$$

Notice now that $q \in \left[ \frac{1}{2}, 1 \right]$ implies $q(2-q) \ge \frac{1+q}{2} \ge \frac{3}{4}$. Therefore, if $q + \frac{\alpha }{2} \ge \alpha + \frac{1}{2}$ then we have $U_E(HH) \ge U_E(HD) = U_E(DH)$, $U_E(HH) \ge U_E(HC_r)$ and $U_E(HH) \ge U_E(DC_r)$. Similarly, if $q + \frac{\alpha }{2} \le \alpha + \frac{1}{2}$ then $U_E(HC_w) \ge U_E(HC_r)$ , $U_E(DC_w) \ge U_E(HD) = U_E(DH)$, and $U_E(DD) \ge U_E(DC_r)$. $\square$

Proof of Theorem 1

Given the result in lemma 1, it is true that

$$\begin{aligned} U_E= & {} \max \{U_E(HH), U_E(DD), U_E(HC_w), U_E(DC_w)\}. \end{aligned}$$

Recall that

$$\begin{aligned} U_E(HH)= & {} \frac{q + \frac{\alpha }{2}}{1 - q (2-q) \beta },\\ U_E(DD)= & {} \frac{\alpha + \frac{1}{2}}{1 - \frac{3}{4} \beta },\\ U_E(HC_w)= & {} \frac{\left( 1-\frac{q}{2}\right) \left( q + \frac{\alpha }{2}\right) + \frac{q}{2} \left( \alpha + \frac{1}{2}\right) }{1 - q (2-q) \beta },\\ U_E(DC_w)= & {} \frac{\frac{1}{4} \left( q + \frac{\alpha }{2}\right) + \frac{3}{4} \left( \alpha + \frac{1}{2}\right) }{1 - \frac{1+q}{2} \beta }. \end{aligned}$$

We need to check the conditions on q, $\beta$ and $\alpha$ under which each of the four different plans above is optimal. We separate the proof in six parts:

Part 1

Plan HH

Since $q(2-q) \ge \frac{1+q}{2} \ge \frac{3}{4}$ then $q + \frac{\alpha }{2} \ge \alpha + \frac{1}{2}$ implies

$$\begin{aligned} U_E(HH) \ge U_E(DD), U_E(HC_w), U_E(DC_w). \end{aligned}$$

Thus, if $q + \frac{\alpha }{2} \ge \alpha + \frac{1}{2}$ then the plan HH is optimal. Moreover, if $q + \frac{\alpha }{2} \le \alpha + \frac{1}{2}$ then it is easy to see that the plan $HC_w$ gives more payoff than the plan HH. Thus, the plan HH is optimal if and only if $q + \frac{\alpha }{2} \ge \alpha + \frac{1}{2}$, which can be rewritten as $\alpha \le 2q - 1$.

Part 2

Plans $HC_w$, $DC_w$ and DD

We proceed by showing first the conditions under which $U_E(HC_w) \ge U_E(DC_w)$, then we show the conditions under which $U_E(DD) > U_E(DC_w)$. Finally we prove that if $U_E(HC_w) \ge U_E(DC_w)$ then $U_E(HC_w) \ge U_E(DD)$ and that if $U_E(DD) > U_E(DC_w)$ then $U_E(DD) > U_E(HC_w)$.

Part 3

Conditions for $U_E(HC_w) \ge U_E(DC_w)$

We have that $U_E(HC_w) \ge U_E(DC_w)$ if and only if

$$\begin{aligned} \frac{\left( 1-\frac{q}{2}\right) \left( q + \frac{\alpha }{2}\right) + \frac{q}{2} \left( \alpha + \frac{1}{2}\right) }{1 - q (2-q) \beta }\ge & {} \frac{\frac{1}{4} \left( q + \frac{\alpha }{2}\right) + \frac{3}{4} \left( \alpha + \frac{1}{2}\right) }{1 - \frac{1+q}{2} \beta }. \end{aligned}$$

Solving for $\alpha$, this can be rewritten as

$$\begin{aligned} \alpha \left( 3 + 2\beta - q(2+11\beta - 8 \beta q) \right)\le & {} q(8 + \beta - q(4+2\beta )) - 3. \end{aligned}$$

(1)

Note now that the expression on the right hand-side is always positive: the minimum of $q(8 + \beta - q(4+2\beta )) - 3$ is achieved at $\beta = 0$ and $q = \frac{1}{2}$ and for those values $q(8 + \beta - q(4+2\beta )) - 3 = 0$.

Consider now that $3 + 2\beta - q(2+11\beta - 8 \beta q) \le 0$, then the condition in (1) is satisfied for any $\alpha$. We have that $3 + 2\beta - q(2 + 11\beta - 8 \beta q) \le 0$ if and only if $\beta \ge \frac{3 - 2q}{q (11-8q) - 2}$. Hence, $U_E(HC_w) \ge U_E(DC_w)$ if $\beta \le \frac{3 - 2q}{q (11-8q) - 2}$.

Assume now that $3 + 2\beta - q(2+11\beta - 8 \beta q) > 0$. In this case from Eq. (1) we obtain

$$\begin{aligned} \alpha\le & {} \frac{q(8 + \beta - q(4+2\beta )) - 3}{3 + 2\beta - q(2+11\beta - 8 \beta q)}. \end{aligned}$$

Hence, if and only if either the inequality above or $\beta \ge \frac{3 - 2q}{q (11-8q) - 2}$ is satisfied, we have that $U_E(HC_w) \ge U_E(DC_w)$.

Part 4

Conditions for $U_E(DD) > U_E(DC_w)$

We have that $U_E(DD) > U_E(DC_w)$ if and only if

$$\begin{aligned} \frac{\alpha + \frac{1}{2}}{1 - \frac{3}{4} \beta }> & {} \frac{\frac{1}{4} \left( q + \frac{\alpha }{2}\right) + \frac{3}{4} \left( \alpha + \frac{1}{2}\right) }{1 - \frac{1+q}{2} \beta }. \end{aligned}$$

Solving for $\alpha$, this can be rewritten as

$$\begin{aligned} \alpha \left( 4 + 5 \beta - 16 \beta q \right)> & {} q(8 + 2\beta ) - \beta - 4. \end{aligned}$$

(2)

Note now that the expression on the right hand-side of (2) is always positive: $q(8+2\beta ) - \beta - 4 = (4 + \beta ) (2q - 1) \ge 0$. Thus, in order for Eq. (2) to be possible, it must be that its left hand side is positive: $4 + 5 \beta - 16 \beta q > 0$. This happens if and only if $\beta < \frac{4}{16q-5}$.

Thus, we have that $U_E(DD) > U_E(DC_w)$ if and only if $\beta < \frac{4}{16q-5}$ and, from Eq. (2),

$$\begin{aligned} \alpha> & {} \frac{q(8+2\beta ) - \beta - 4}{4 + 5 \beta - 16 \beta q}. \end{aligned}$$

Part 5

$U_E(HC_w) \ge U_E(DC_w)$ implies $U_E(HC_w) \ge U_E(DD)$

Assume first that $U_E(HC_w) \ge U_E(DC_w)$ and $\beta \ge \frac{3 - 2q}{q (11-8q) - 2}$. We have that $\beta \ge \frac{3 - 2q}{q (11-8q) - 2}$ implies $\beta \ge \frac{4}{16q-5}$. This is because

$$\begin{aligned} \frac{3 - 2q}{q (11-8q) - 2}\ge & {} \frac{4}{16q-5} \end{aligned}$$

if and only if $q \ge \frac{1}{2}$, which is true in our case.

Since $\beta \ge \frac{4}{16q-5}$ implies that $U_E(DD) \le U_E(DC_w)$ (see part 4 of the proof), we have that $U_E(HC_w) \ge U_E(DC_w)$ and $\beta \ge \frac{3 - 2q}{q (11-8q) - 2}$ implies $U_E(HC_w) \ge U_E(DD)$.

Assume now that $U_E(HC_w) \ge U_E(DC_w)$ but $\beta < \frac{3 - 2q}{q (11-8q) - 2}$. In this case, we must have (see part 3 of the proof)

$$\begin{aligned} \alpha\le & {} \frac{q(8 + \beta - q(4+2\beta )) - 3}{3 + 2\beta - q(2+11\beta - 8 \beta q)}. \end{aligned}$$

We now show that the inequality above together with $\beta < \frac{4}{16q-5}$ (necessary condition for $U_E(DD) > U_E(DC_w)$) implies

$$\begin{aligned} \alpha\le & {} \frac{q(8+2\beta ) - \beta - 4}{4 + 5 \beta - 16 \beta q}, \end{aligned}$$

and, hence, $U_E(DD) \le U_E(DC_w)$.

We have that

$$\begin{aligned} \frac{q(8 + \beta - q(4+2\beta )) - 3}{3 + 2\beta - q(2+11\beta - 8 \beta q)}\le & {} \frac{q(8+2\beta ) - \beta - 4}{4 + 5 \beta - 16 \beta q} \end{aligned}$$

if and only if

$$\begin{aligned} (2q-1) ((2+\beta )q-3) (\beta (16q-5)-4)\ge & {} 0. \end{aligned}$$

Since $2q-1 \ge 0$, $(2+\beta )q-3 \le 0$ and $\beta (16q-5)-4 < 0$ given that $\beta < \frac{4}{16q-5}$, the inequality above is true. Hence, whenever $U_E(HC_w) \ge U_E(DC_w)$ we have $U_E(DD) \le U_E(DC_w)$ as required. Therefore, plan $HC_w$ is optimal if and only if plan HH is not optimal ($\alpha < 2q - 1$) and the conditions for $U_E(HC_w) \ge U_E(DC_w)$ are satisfied.

Part 6

$U_E(DD) > U_E(DC_w)$ implies $U_E(DD) > U_E(HC_w)$

If $U_E(DD) > U_E(DC_w)$ then it must be that $\beta < \frac{4}{16q-5}$ and

$$\begin{aligned} \alpha> & {} \frac{q(8+2\beta ) - \beta - 4}{4 + 5 \beta - 16 \beta q}. \end{aligned}$$

However, as shown in part 5, this implies that

$$\begin{aligned} \alpha> & {} \frac{q(8 + \beta - q(4+2\beta )) - 3}{3 + 2\beta - q(2+11\beta - 8 \beta q)}. \end{aligned}$$

Which in turn implies that $U_E(HC_w) < U_E(DC_w)$. Thus, $U_E(DD) > U_E(DC_w)$ implies $U_E(HC_w) < U_E(DC_w)$.

Note that the condition

$$\begin{aligned} \frac{q(8+2\beta ) - \beta - 4}{4 + 5 \beta - 16 \beta q}> & {} 2q-1 \end{aligned}$$

can be rewritten as $\beta (-8q^2 + 6q - 1) < 0$, which is true for any $q \ge \frac{1}{2}$. Hence, whenever $U_E(DD) > U_E(DC_w)$ it is true that $\alpha > 2q-1$ and, thus, plan HH is not optimal.

Summing up, if $U_E(DD) > U_E(DC_w)$ then $U_E(HC_w) < U_E(DC_w)$ and plan HH is not optimal. Therefore, plan DD is optimal if and only if the conditions for $U_E(DD) > U_E(DC_w)$ are satisfied. $\square$

Proof of Result 1

The politician is honest for as long as he has not guaranteed himself re-election if he is honest in period 1 (before period 1 is resolved he has not had the chance to secure re-election yet) and if he is honest in period 2 at least in the situations where he did not take the public decision in period 1. Thus, we have to show that there are values of q and $\beta$ for which for any value of $\alpha$ either the plan HH or the plan $HC_w$ are optimal.

Assume first that $\alpha \le 2q - 1$. By Theorem 1 the optimal plan is HH, which means that the politician is honest in both periods.

Assume now that $\alpha > 2q - 1$. If $\beta \ge \frac{3 - 2q}{q (11-8q) - 2}$ then by Theorem 1 the optimal plan is $HC_w$ which means that the politician is honest in the first period and honest again in the second period if he did not take the public decision in the first period. Note that $\beta \ge \frac{3 - 2q}{q (11-8q) - 2}$ is only possible if $q \ge \frac{5}{8}$ as otherwise $\frac{3 - 2q}{q (11-8q) - 2} > 1$. This completes the proof. $\square$

Proof of Result 2

Assume that $\beta < \frac{3 - 2q}{q (11-8q) - 2}$. By Theorem 1 we have that in this case $HC_w$ is the optimal plan if and only if

$$\begin{aligned} \alpha\le & {} \frac{q(8 + \beta - q(4+2\beta )) - 3}{3 + 2\beta - q(2+11\beta - 8 \beta q)}. \end{aligned}$$

We now show that the right hand side of this expression is increasing in q at $q = \frac{1}{2}$ and decreasing in q at $q = 1$ for $\beta \ge \frac{1}{4}$. By continuity this means that the value of $\alpha$ for which $HC_w$ is the optimal plan is non-monotonic in q.

The sign of the derivative of

$$\begin{aligned} \bar{\alpha }(q, \beta ) = \frac{q(8 + \beta - q(4+2\beta )) - 3}{3 + 2\beta - q(2+11\beta - 8 \beta q)} \end{aligned}$$

with respect to q is equal to the sign of

$$\begin{aligned}&(8 + \beta - 2q(4+2\beta )) (3 + 2\beta - q(2+11\beta - 8 \beta q) \\&\quad -\,(q(8 + \beta - q(4+2\beta )) - 3) (-(2 + 11\beta - 16 \beta q)). \end{aligned}$$

The expression above evaluated at $q = 1$ equals $2 (1-\beta ) (1-4\beta )$ which is negative if $\beta > \frac{1}{4}$. The expression above evaluated at $q = \frac{1}{2}$ equals $(4-\beta ) (2 - \frac{3}{2} \beta )$, which is positive. Thus, since the expression $\bar{\alpha }(q, \beta )$ is continuous in q then the region above its graph is non-convex for $\beta > \frac{1}{4}$, which proves that the value of $\alpha$ for which $HC_w$ is the optimal plan can be non-monotonic in q.¹⁰

Figure 2 shows that the assumptions imposed on the parameters of the model in this proof are non-empty and, thus, the monotonicity can indeed exist. $\square$