Abstract
We characterize the outcome of majority voting for single-peaked preferences on median spaces. This large class of preferences covers a variety of multi-dimensional policy spaces including products of lines (e.g. grids), trees, and hypercubes. Our main result is the following: If a Condorcet winner (i.e. a winner in pairwise majority voting) exists, then it coincides with the appropriately defined median (“the median voter”). This result generalizes previous findings which are either restricted to a one-dimensional policy space or to the assumption that any two voters with the same preference peak must have identical preferences. The result applies to models of spatial competition between two political candidates. A bridge to the graph-theoretic literature is built.


Similar content being viewed by others
Notes
Sometimes slightly weaker or slightly stronger notions are considered (cf., e.g. Bandelt 1985).
In particular, for any median space there is a graph \((X,E)\) that represents it in the sense that \((x,y,z)\in T_\mathcal{H }\) if and only if y lies on a shortest path between x and z.
We refer to the median alternative, not the median voter, because in this framework there need not be any voter with preference peak equal to median alternative.
By definition a would win a majority voting on the issues (Nehring and Puppe 2007b), but not majority voting on the alternatives.
The latter point will be illustrated in Example 2.
For convenience, we let A be the winning candidate in case of a tie. If \(s^{A}=s^{B}\), then this convention does not matter.
This modeling approach was made prominent by Downs (1957) who writes: “political parties in a democracy formulate policy strictly as a means of gaining votes. They do not seek to gain office in order to carry out certain preconceived policies or to serve any particular interest groups; rather they formulate policies and serve interest groups in order to gain office.” The Downsian approach has been critized by Roemer (2001), among others.
This idea is similar to the “citizen-candidates” introduced in Osborne and Slivinski (1996).
One could argue that if the opponent has very similar preferences, a reformist’s incentive to run for election might just not be strong enough.
An interesting variation of the two games \(\Gamma ^{\succeq }\) and \(\tilde{\Gamma }^{\succeq }\) is to consider the competition of one Downsian candidate and one reformist. It turns out that, similar to the violation of sufficient heterogeneity between reformists, both candidates choosing the Condorcet winner is a Nash equilibrium, but generically there are other Nash equilibria with different outcomes.
A path from x to y is a sequence of distinct nodes \((x_{1},\ldots ,x_{T})\) such that \(x_{1}=x, \,x_{T}=y\), and \(x_{t}x_{t+1}\in {E}\) for all \(t\in \{1,\ldots ,T-1\}\). We focus on graphs that are connected, i.e. there exists a path between any pair of nodes, and we define \(d(x,x)=0\) for any node x and any graph.
In particulr, these median graphs satisfy that for any triple of nodes \(x,y,z\in X\), there is exactly one node m, which is graphicly between each pair of the triple. Median graphs are well-studied objects and contain lines, trees, products of lines (grids), and hypercubes, as special cases (Van de Vel 1993).
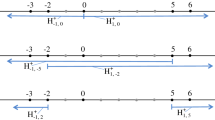
The restrictiveness of the assumption of single-peakedness depends on the graph structure, e.g. for the line graph we have the standard notion of single-peakedness, while for the complete graph, we obtain the unrestricted domain (Nehring and Puppe 2007b).
Thus, fixing a graph and a distribution of preference peaks, there are many profiles of single-peaked preferences, while only one of them is distance-based.
Median graphs that are not trees might well admit a Condorcet winner for many profiles of single-peaked preferences. For example, a Condorcet Winner did not exist for the profile \(\succeq \) given in Example 1. If we consider a change of preferences of voters 2 and 3 such that \(\succeq ^{\prime }_{2}=(b,a,d,c),\, \succeq ^{\prime }_{3}=(c,a,d,b)\), i.e. these voters now prefer a over d, then the Weber point, alternative a, becomes a Condorcet winner. Other nodes can never be Condorcet winners for single-peaked preferences on this graph (by Proposition 1).
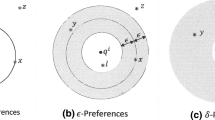
A Weber point certainly exists but need not be unique.
Since \(\mathcal K \) is a smallest circle, this is the only type of additional paths that are shortest paths between two members of the circle.
Note that a voter (e.g. voter 1) whose preference peak (alternative a) has several shortest paths to the opposite member of the circle (alternative d), must prefer all nodes on this path (a subset of Y) over the opposite member of the circle (alternative d). This is, however, the only restriction on the preference ranking between alternatives in Y and alternatives on the circle for such a voter.
References
Ballester M, Haeringer G (2011) A characterization of the single-peaked domain. Soc Choice Welf 36(2):305–322
Bandelt H-J (1985) Networks with Condorcet solutions. Eur J Oper Res 20(3):314–326
Bandelt H-J, Barthélémy J-P (1984) Medians in median graphs. Discret Appl Math 8(2):131–142
Black D (1948) On the rationale of group decision-making. J Polit Econ 56(1):23–34
Congleton R (2002) The median voter model. In: Rowley F, Schneider RK (eds) The Encyclopedia of public choice. Kluwer Academic Publishers, Dordrecht
Demange G (1982) Single-peaked orders on a tree. Math Soc Sci 3(4):389–396
Demange G (2011) Majority relation and median representative ordering. J Span Econ Assoc, 1–15
Downs A (1957) An economic theory of democracy. Harper and Row, New York
Eaton BC, Lipsey RG (1975) The principle of minimum differentiation reconsidered: some new developments in the theory of spatial competition. Rev Econ Stud 42(1):27–49
Eiselt HA, Laporte G (1989) Competitive spatial models. Eur J Oper Res, 39–231
Eiselt HA, Laporte G (1993) The existence of equilibria in the 3-facility Hotelling model in a tree. Transp Sci 27(1):39–43
Hansen P, Thisse JF, Wendell RE (1986) Equivalence of solutions to network location problems. Math Oper Res 11:672–678
Hotelling H (1929) Stability in competition. Econ J 39(153):41–57
Moulin H (1980) On strategy-proofness and single peakedness. Public Choice 35(4):437–455
Moulin H (1984) Generalized Condorcet-winners for single peaked and single-plateau preferences. Soc Choice Welf 1:127–147. doi:10.1007/BF00452885
Nehring K, Puppe C (2007a) Efficient and strategy-proof voting rules: a characterization. Games Econ Behav 59(1):132–153
Nehring K, Puppe C (2007b) The structure of strategy-proof social choice. Part I: general characterization and possibility results on median spaces. J Econ Theory 135(1):269–305
Osborne MJ, Slivinski A (1996) A model of political competition with citizen-candidates. Q J Econ 111(1):65–96
Roemer JE (2001) Political competition: theory and applications. Harvard University Press, Cambridge
Van de Vel M (1993) Theory of convex structures. North-Holland
Wendell RE, McKelvey RD (1981) New perspectives in competitive location theory. Eur J Oper Res 6(2):174–182
Acknowledgments
I thank Veronica Block, Dinko Dimitrov, Jan-Philip Gamp, Anke Gerber, Claus-Jochen Haake, Tim Hellmann, Dominik Karos, Gerd Muehlheusser, Clemens Puppe, Nils Roehl, Walter Trockel, and the participants of the “Public Economic Theory (PET 10)” Conference in Istanbul and the “SING 9” Workshop in Budapest for helpful discussions and comments. Moreover, this paper has benefited from the suggestions of two anonymous referees.
Author information
Authors and Affiliations
Corresponding author
Appendix: Proof of Proposition 3
Appendix: Proof of Proposition 3
Proposition 3
(Existence) A graph \((X,E)\) guarantees existence of a Condorcet winner for any profile of single-peaked preferences if and only if it is a tree.
Proof
We have to prove two directions.
-
IF
Suppose \(\succeq \) is a profile of single-peaked preferences on a tree graph \((X,E)\). Let \(q\) be a Weber point, i.e. \(q\in \arg \min _{x\in X}\sum _{i\in N}{d(x,x_i^*)} \).Footnote 16 Consider any alternative \(x\ne q\). We will show that x cannot be preferred over q by a majority of voters. Since \((X,E)\) is a tree graph, there is a unique path between q and x. Let \(N(q):=\{y\in X \mid qy\in E \}\), i.e. the set of graphic neighbors of node q. Let y be the neighbor of q that lies graphicly between q and x, i.e. \(y\in N(q)\) such that \((x,y,q)\in T_E\). Since trees are connected without circles, we have for any node z, either \(d(z,y)<d(z,q)\) or \(d(z,q)<d(z,y)\). A well-known result on tree graphs is that for a profile of peaks \((x^*_i)_{i\in N}\) a Weber point q satisfies \(\forall y\in N(q), \,\# \{i\in N \; | \; d(x_i^*,q)<d(x_i^*,y) \}\ge \frac{n}{2}\) (cf., e.g. Bandelt and Barthélémy 1984). Thus, for at least \(\frac{n}{2}\) voters we have \(d(x_i^*,q)<d(x_i^*,y)\), which means that \((x_i^*,q,x)\in T_E\) such that single-peakedness implies \(q\succ _i x\).
-
ONLY IF
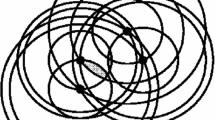
For any graph that is not a tree, we will provide a single-peaked preference profile of three voters such that there is no Condorcet winner. Trees are connected and cyclic. Recall that a circle (or cycle) \(\mathcal K \) is a sequence of \(K(\ge 3)\) distinct nodes \((x_{1},\ldots ,x_{K})\) such that \(x_{k}x_{k+1}\in {E}\) for all \(k\in \{1,\ldots ,K-1\}\) and \(x_Kx_1 \in E\). We first consider unconnected graphs (case 1), then connected graphs where the smallest circle is of odd length (case 2), and finally connected graphs where the smallest circle is of even length (case 3).
-
Case 1 \((X,E)\) is unconnected. Then there are two nodes, say \(a\) and \(b\), which are not connected by any path. Let c be some other node. Note that none of the three nodes \(a,\, b,\, c\) is graphicly between the two others. Denote \(R:=X\setminus \{a,b,c \}\). Consider three voters N with the following strict preference orderings: \((a,b,c,\sigma _1(R) ),\, (b,c,a, \sigma _2(R) )\), and \((c,a,b,\sigma _3(R) )\), where \(\sigma _i\) are orders on R which do not violate single-peakedness. This profile of preferences is single-peaked on \((X,E)\). In majority voting any alternative in R is strictly defeated, while among the three alternatives \(a,\, b, \,c\), we have the classic Condorcet cycle.
-
Case 2 \((X,E) \) is connected and the smallest circle is of odd length K. If \(K=3\), denote a smallest circle by \(\mathcal K =(a,b,c )\) and let \(R:=X\setminus \{a,b,c \}\). Consider three voters with preferences on \(a,\, b,\, c\) exactly as in case 1 and the preferences on the rest R are added in some single-peaked order \(\sigma _i\). This profile of preferences is single-peaked on \((X,E)\). There is no Condorcet winner such as in case 1. Now, let \(K\ge 5\). Let us consider one smallest circle \(\mathcal K \) and label it as follows: \(\mathcal K =(a,b_1,b_2,\ldots , b_{\frac{K-1}{2}},d, c_{\frac{K-1}{2}-1}, c_{\frac{K-1}{2}-2}, \ldots ,c_1)\) such as illustrated in Fig. 3 panel (a). Let Z denote the set of nodes on the circle. Now, consider three voters with the following strict preference orderings:
$$\begin{aligned} \succeq _1&= (a,b_1,c_1,b_2,c_2,\ldots ,b_{\frac{K-1}{2}-1},c_{\frac{K-1}{2}-1},b_{\frac{K-1}{2}},d,\sigma _1(X\setminus Z)) \\ \succeq _2&= (b_1,b_2,\ldots ,b_{\frac{K-1}{2}},d,a,c_1,c_2,\ldots ,c_{\frac{K-1}{2}-1}, \sigma _2(X\setminus Z))\\ \succeq _3&= (c_1,c_2,\ldots ,c_{\frac{K-1}{2}-1},d,a,b_1,b_2,\ldots ,b_{\frac{K-1}{2}}, \sigma _3(X\setminus Z)), \end{aligned}$$where the alternatives in \(X\setminus Z\) are listed in some single-peaked order \(\sigma _i\). Since \(\mathcal K \) is a smallest circle, there are no paths between members of the circle which are shorter than the shortest path on the circle. Thus, there is no node \(y\in X\setminus Z\) such that \((x,y,z)\in T_E\) for some \(x,z \in Z\). Therefore, the profile \(\succeq \) is single-peaked on \((X,H)\). In majority voting alternative a defeats any alternative except d. \(b_1\) defeats d and, finally, d defeats a.
-
Case 3 \((X,E) \) is connected and the smallest circle is of even length K. Let us consider one smallest circle \(\mathcal K \) and label it as follows: \(\mathcal K =(a,b_1,b_2,\ldots , b_{\frac{K}{2}-1},d, c_{\frac{K}{2}-1}, c_{\frac{K}{2}-2}, \ldots ,c_1)\) such as illustrated in Fig. 3 panel (b). Let Z denote the set of nodes on the circle. Any pair \(x,y\in Z\) has a shortest path using only nodes of the circle. However, there might be additional shortest paths for pairs at the opposite sides of the circle, i.e. when \(d(x,y)=\frac{K}{2}\).Footnote 17 Let Y denote the set of all nodes that belong to such a path but not to the circle, i.e. \(Y:=\{y\in X\setminus Z \; | \; \exists x,z\in Z \text{ with } (x,y,z)\in T_E \}\), and let \(R:=X\setminus (Z\cup Y)\). Now, consider three voters with the following strict preference orderings:
$$\begin{aligned} \succeq _1&= (a,b_1,c_1,b_2,c_2,\ldots ,b_{\frac{K}{2}-1},c_{\frac{K}{2}-1},\sigma _1(Y), d, \tilde{\sigma }_1(R)) \\ \succeq _2&= (b_1,b_2,\ldots ,b_{\frac{K}{2}-1},d,a,c_1,c_2,\ldots ,c_{\frac{K}{2}-2},\sigma _2(Y),c_{\frac{K}{2}-1}, \tilde{\sigma }_2(R))\\ \succeq _3&= (c_1,c_2,\ldots ,c_{\frac{K}{2}-1},d,a,b_1,b_2,\ldots ,b_{\frac{K-1}{2}-2}, \sigma _3(Y),b_{\frac{K-1}{2}-1}, \tilde{\sigma }_3(R)), \end{aligned}$$where \(\sigma _i\) (resp. \(\tilde{\sigma }_i\)) puts the alternatives in Y (resp. R) in some single-peaked order. As it can be checked, this profile \(\succeq \) is single-peaked on \((X,H)\).Footnote 18 In majority voting alternative a defeats any alternative except d. \(b_{1}\) defeats d and, finally, d defeats a.
\(\square \)
Rights and permissions
About this article
Cite this article
Buechel, B. Condorcet winners on median spaces. Soc Choice Welf 42, 735–750 (2014). https://doi.org/10.1007/s00355-013-0744-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00355-013-0744-0