Skip to main content
SpringerLink
Log in

A novel method for three-dimensional three-component analysis of flows close to free water surfaces

  • Research Article
  • Published:
Experiments in Fluids Aims and scope Submit manuscript

Abstract

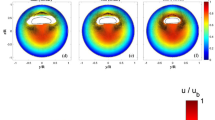
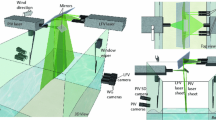
Initial effort is made to establish a new technique for the measurement of three-dimensional three-component (3D3C) velocity fields close to free water surfaces. A fluid volume is illuminated by light emitting diodes (LEDs) perpendicularly to the surface. Small spherical particles are added to the fluid, functioning as a tracer. A monochromatic camera pointing to the water surface from above records the image sequences. The distance of the spheres to the surface is coded by means of a supplemented dye, which absorbs the light of the LEDs according to Beer–Lambert’s law. By applying LEDs with two different wavelengths, it is possible to use particles variable in size. The velocity vectors are obtained by using an extension of the method of optical flow. The vertical velocity component is computed from the temporal brightness change. The setup is validated with a laminar falling film, which serves as a reference flow. Moreover, the method is applied to buoyant convective turbulence as an example for a non stationary, inherently 3D flow.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Notes

  1. Though Debaene et al. (2005) were interested in the flow field close to a rigid wall, the authors of this paper ultimately want to measure the velocity field close to a free surface. As long as this surface is not bent, the coordinate z represents the distance of the particle’s surface, which is orthogonal to the flat surface.

References

  • Agüi JC, Jimenez J (1987) On the performance of particle tracking. J Fluid Mech 185:261–304

    Article  Google Scholar 

  • Banner ML, Phillips OM (1974) On the incipient breaking of small scale waves. J Fluid Mech 65:647–656

    Article  MATH  Google Scholar 

  • Bannerjee S, MacIntyre S (2004) The air–water interface: turbulence and scalar interchange. In: Liu PLF (eds) Advances in coastal and ocean engineering, vol 9. World Scientific, Hackensack, pp 181–237

  • Brücker C (1995) Digital-particle-image-velocimetry (dpiv) in a scanning light-sheet: 3d starting flow around a short cylinder. Exp Fluids 19:255–263

    Article  Google Scholar 

  • Bukhari SJK, Siddiqui MHK (2006) Turbulent structure beneath air–water interfaces during natural convection. Phys Fluids 18:035106

    Article  Google Scholar 

  • Cowen E, Monismith S (1997) A hybrid digital particle tracking velocimetry technique. Exp Fluids 22:199–211

    Article  Google Scholar 

  • Debaene P, Kertzscher U, Gouberits I, Affeld K (2005) Visualization of a wall shear flow. J Vis 8(4):305–313

    Article  Google Scholar 

  • Elsinga GE, Scarano F, Wieneke B (2006) Tomographic particle image velocimetry. Exp Fluids 41:933–947

    Article  Google Scholar 

  • Haussecker HW, Fleet DJ (2001) Computing optical flow with physical models of brightness variation. PAMI 23(6):661–673

    Google Scholar 

  • Haußecker H, Jähne B (1997) A tensor approach for precise computation of dense displacement vector fields. In: Paulus E, Wahl FM (eds) DAGM. Springer, Braunschweig, pp 199–208

    Google Scholar 

  • Hering F (1996) Lagrangesche Untersuchungen des Strömungsfeldes unterhalb der wellenbewegten Wasseroberfläche mittels bildfolgenanalyse. PhD Thesis, University of Heidelberg

  • van de Hulst HC (ed) (1981) Light scattering by small particles. Dover Publications, New York

  • Jähne B, Haußecker H (1998) Air–water gas exchange. Ann Rev Fluid Mech 30:443–468

    Article  Google Scholar 

  • Jehle M (2006) Spatio-temporal analysis of flows close to water surfaces. Diss, Univ Heidelberg

  • Li H, Sadr R, Yoda M (2006) Multilayer nano-particle image velocimetry. Exp Fluids 41:185–194

    Article  Google Scholar 

  • Maas HG, Gruen A, Papantoniou D (1993) Particle tracking velocimetry in three-dimensional flows. Part I: Photogrammetric determination of particle coordinates. Exp Fluids 15:133–146

    Article  Google Scholar 

  • Melville WK, Shear R, Veron F (1998) Laboratory measurements of the generation and evolution of langmuir circulations. J Fluid Mech 364:31–58

    Article  MATH  Google Scholar 

  • Okuda K (1982) Internal flow structure of short wind waves, part i–iv. J Oceanogr Soc Japan 38:28–42

    Article  Google Scholar 

  • Peirson WL, Banner ML (2003) Aqueous surface layer flows induced by microscale breaking wind waves. J Fluid Mech 479:1–38

    Article  MATH  MathSciNet  Google Scholar 

  • Raffel M, Willert C, Kompenhans J (1998) Particle image velocimetry. A practical guide. Springer, Heidelberg

    Google Scholar 

  • Rayleigh L (1916) On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side. Philos Mag 32:529

    Google Scholar 

  • Tropea C, Foss J, Yarin A (2007) Springer handbook of experimental fluid dynamics. Springer, Heidelberg, pp 8, 10, 11

Download references

Acknowledgments

We gratefully acknowledge the support by the German Research Foundation (DFG, JA 395/11-2) within the priority program “Bildgebende Messverfahren für die Strömungsanalyse”.

Author information

Authors and Affiliations

  1. Laboratoire d’Etudes Aérodynamiques (UMR 6609-CNRS), Boulevard Pierre et Marie Curie Téléport 2, B.P. 30179, 86960, Futuroscope Poitiers Cedex, France

    M. Jehle

  2. Interdisciplinary Center for Scientific Computing, Heidelberg University, Im Neuenheimer Feld 368, 69120, Heidelberg, Germany

    B. Jähne

Authors
  1. M. Jehle
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. B. Jähne
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Jehle.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Jehle, M., Jähne, B. A novel method for three-dimensional three-component analysis of flows close to free water surfaces. Exp Fluids 44, 469–480 (2008). https://doi.org/10.1007/s00348-007-0453-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00348-007-0453-5

Keywords

Search

Navigation