Single-slit focusing and its representations

Abstract

We illustrate the phenomenon of the focusing of a freely propagating rectangular wave packet using three different tools: (1) the time-dependent wave function in position space, (2) the Wigner phase-space approach, and (3) an experiment using laser light.

1 Introduction

In July 1816, the civil engineer Augustin-Jean Fresnel published his preliminary results [1] confirming the wave theory of light. Three years later he participated with his Mémoire sur la Diffraction de la Lumière in the Grand Prix of the French Academy of Sciences [2]. It was on this occasion that Siméon Poisson predicted that an opaque disc illuminated by parallel light would create a bright spot in the center of a shadow. This phenomenon was experimentally confirmed by Francois Arago and led to the victory of the wave over the particle theory. In the present article we discuss an effect related to the Poisson spot which is the one-dimensional analogue of the camera obscura [3, 4].

Indeed, we have recently found [5] that a rectangular matter wave packet which undergoes free time evolution according to the Schrödinger equation focuses before it spreads. This phenomenon has been confirmed for light [6], water and surface plasmon waves [7]. In the present article we illustrate this effect in Wigner phase space and verify it using classical light in real space.

Our article is organized as follows: in Sect. 2 we first give a brief history of the diffraction of waves, and then review several focusing effects especially those associated with the phenomenon of diffraction in time introduced in Moshinsky [8].

We dedicate Sect. 3 to the discussion of the focusing of a rectangular wave packet from the point of view of the time-dependent wave function. In particular, we show this effect manifests itself in the time-dependent probability density as well as the Gaussian width [5] of the wave packet. For this purpose we derive exact as well as approximate analytical expressions for the time-dependent probability amplitude and density.

In Sect. 4 we verify these predictions reporting on an experiment using laser light diffracted from a single slit. Here we take advantage of the analogy between the paraxial approximation of the Helmholtz equation of classical optics and the time-dependent Schrödinger equation of a free particle. We measure the intensity distributions of the light in the near-field of the slits and obtain the Gaussian width of the intensity field. Moreover, we make contact with the predictions of non-paraxial optics.

Section 5 illuminates this focusing effect from quantum phase space using the Wigner function. In particular, we show that the phenomenon of focusing which reflects itself in a dominant maximum of the probability density on the optical axis follows from radial cuts through the initial Wigner function at different angles with respect to the momentum axis. Moreover, we analyze the rays and envelopes of the Wigner function in more detail.

We conclude in Sect. 6 by summarizing our results and by providing an outlook. Here we allude to the influence of the number of dimensions on the focusing and emphasize the importance of corrections to paraxial optics.

To keep our article self-contained while focusing on the central ideas we have included three appendices. Indeed, “Appendix A” contains the calculations associated with the Gaussian width of our wave packet and “Appendix B” presents a detailed discussion of the Wigner function approach towards diffractive focusing. As an outlook we compare in “Appendix C” the paraxial and non-paraxial results obtained for diffraction by slits and circular apertures.

2 Diffraction theory

In this section we first provide a historical overview of diffraction and then address the phenomenon of diffractive focusing. Due to their different nature we distinguish in this discussion between light and matter waves. Moreover, we briefly review the concept of diffraction in time.

2.1 A brief history

Following the experimental demonstration of the wave nature of light by Thomas Young [9] and the first theory on diffraction by Fresnel [1] the nineteenth century was extremely successful in the investigation of wave phenomena, specially in optics. The unifying electromagnetic theory of James Clerk Maxwell [10] was the culmination of all previous developments on electromagnetism. Gustav Kirchhoff readdressed the diffraction of scalar waves and put it on a rigorous mathematical foundation [11]. The Fresnel diffraction arises now as a special case of the Kirchhoff diffraction. Arnold Sommerfeld and Lord Rayleigh [4, 12, 13] improved the Kirchhoff theory correcting the boundary conditions at the aperture and with that eliminating the discrepancy arising between the solutions and the boundary conditions chosen by Kirchhoff. Friedrich Kottler proposed another reason for this discrepancy by showing that the Kirchhoff integral can be interpreted not as a solution of the boundary value problem but as a solution for the “saltus” at the boundary [14, 15]. Moreover, he extended the scalar theory to electromagnetic waves [16, 17].

During the twentieth century numerous theoretical and experimental contributions to diffraction theory emerged. Julius Stratton and Lan Jen Chu extended the scalar Kirchhoff diffraction theory to vector waves [18] accounting for polarization. Hans Bethe found analytical solutions for the diffraction of electromagnetic waves by an aperture much smaller than the wavelength [19]. His theory and the corrections later introduced by Christoffel Bouwkamp [20] became important because of the invention of the near-field scanning microscope (SNOM or NSOM) [21] and the developments related to near-field optics [22–24]. In 1998, Thomas Ebbesen and collaborators observed that light transmission through an array of subwavelength apertures drilled in noble metal thin films can largely surpass the value predicted by Bethe [25]. This extraordinary optical transmission is dependent on the geometry of the array, on the illumination conditions and on the size and shape of the apertures [26, 27]. It results from the excitation of surface plasmon modes near the aperture. In plasmonic gratings with narrow slits it may also lead to an attenuation of the transmitted light stronger than that predicted by the Bethe–Bouwkamp theory [28].

2.2 Focusing of waves

Focusing of waves by diffraction due to slits or apertures falls into two categories: (1) near-field focusing effects arising mainly in the diffraction of electromagnetic waves, and (2) focusing resulting from diffraction of slits or apertures larger than the wave length, where the focus is located in the Fresnel zone.

In the first category we include the focusing of light resulting from the confinement of surface plasmons in nanostructured apertures in plasmonic materials [25, 26, 29]. Frequently scalar and electromagnetic diffraction theories assume the apertures to be located in infinite and perfectly absorbing screens, and thus surface plasmons are ignored. Hence, these theories cannot account for plasmonic modes and their optical effects. To accurately describe the effects produced by the excitation of surface plasmons a full electromagnetic theory using the optical properties of real materials is required.

The focusing of light by apertures smaller than the wave length has been investigated theoretically several times in the last decades [30, 31]. However, this near-field focusing is dependent on the polarization of light and restricted to small apertures.

The properties of the focus in laser beams and atomic beams is of interest in microscopy and atom optics. Standard laser beams such as Laguerre–Gaussian, or Hermite–Gaussian beams can be strongly focused. The smallest order Hermite–Gaussian beam called TEM$_{00}$ has the highest confinement and is, therefore, preferred in confocal microscopy. Other beams such as Airy and Bessel beams [32, 33] have non-diffracting properties.

To increase the field confinement, and thus the resolution of a microscope, novel laser beams and illumination mechanisms have been proposed [22, 29, 34–36].

In parallel, a similar interest exists in the confinement and squeezing of matter wave packets [37–39]. Focusing effects in atomic beams resulting from the interaction with laser fields diffracted by apertures in metallic screens were investigated recently [40]. Indeed, the interaction of matter waves with light fields has been the subject of intensive research in atom and quantum optics [41]. However, this spatial confinement, or focusing is of different nature than that of diffraction. In the latter, the field confinement created is solely determined by the properties of the incoming wave and the aperture. No other optical element is involved.

Self-focusing of light may also arise in nonlinear media [42]. However, we will not discuss this phenomenon in this article, but rather concentrate in our analysis in the focusing effects arising from diffraction in free space due to slits larger than the wavelength.

In 2012, the focusing of light waves by a slit larger than the wavelength was experimentally observed [6]. The diffraction pattern is similar to that of a circular aperture of several wavelengths in diameter [43, 44]. The main difference between a slit and a circular aperture is the value of the dominant maximum, relative to the intensity of the incident wave. For a circular aperture it reaches 4.0, whereas for a slit is only 1.8 stronger than the incoming wave [6, 43].

The diffraction patterns of slits and circular apertures for scalar waves and non-polarized electromagnetic waves can be accurately calculated using the Rayleigh–Sommerfeld diffraction integrals, even in the case of apertures of the size of the wavelength, without using any mathematical approximation. Moreover, analytical solutions for the on-axis field intensity were found for the circular aperture [43, 45], and the oscillations of the intensity on-axis were confirmed for electromagnetic waves [44, 46].

2.3 Diffraction in time

Moshinsky [8] introduced the concept of diffraction in time using matter waves. Remarkably the time evolution of the probability density of a wave packet suddenly released by a shutter is mathematically identical to the intensity pattern behind a semi-infinite plane. This analogy stands out most clearly when we substitute the time coordinate of the wave packet by the corresponding space coordinate in diffraction. Then the solution of the Schrödinger equation for the problem of the Moshinsky shutter is identical to that of the Fresnel diffraction by a semi-infinite plane, and the probability density reaches a maximum of 1.3. Moreover, Moshinsky analyzed later the time–energy uncertainty associated with the shutter arrangement [47] and Godoy investigated the Fresnel and Fraunhofer diffraction in time of initially stationary states [48].

Recently, the diffraction in time of the double-shutter problem was analyzed [5]. An initially confined rectangular wave packet in one dimension is suddenly released and evolves in time. Again, the solution of the corresponding Schrödinger equation has the same form as the Fresnel diffraction of scalar waves by a single slit of infinite length.

However, we emphasize that Fresnel diffraction only holds true in the paraxial approximation of optics. The general solution of the diffraction by a slit is found by solving the Kirchhoff, or the Rayleigh–Sommerfeld diffraction integrals.

The mathematical analysis of the classical diffraction problems makes use of wave functions expressed in real, or reciprocal space. It is also very common in the investigation of the diffraction of matter waves [8, 49–51].

However, since Wigner introduced his famous distribution function [52] an increasing number of publications has used the Wigner phase space representation to study the dynamics of light beams [53–57] and matter waves [58–65]. Other phase space distribution functions related to the Wigner function have been also used in matter waves phenomena. They are interrelated and belong to the Cohen class [66]. In this article we employ both the wave function and the Wigner representations of matter wave packets.

The evolution in time of matter waves with zero angular momentum, so-called s-waves, strongly depends on the number of space dimensions [67]. For instance, in two dimensions, an initial ring-shaped wave packet first contracts reaching a minimum, reducing the radius of the ring, and then monotonically expands. In three dimensions, the radius only increases. This effect is attributed to a quantum anti-centrifugal force [67–69]. This example shows that the focusing effect of a free wave packet is a more general phenomenon than that arising from the free time evolution of a one-dimensional rectangular wave packet.

We conclude with a brief reference to the type of boundaries of the slit, or shutter. Most of the classical treatments of diffraction problems define the edges of the slit, or of other aperture shape as sharp transitions between a perfectly absorbing surface and a homogeneous fully transmitting medium. In quantum matter waves, the Moshinsky shutter or the sudden release of rectangular wave packet is also an example of sharp boundaries. The effects arising in the diffraction patterns due to non-sharp boundaries have been investigated recently [5, 50, 70–73].

3 Wave function approach

In this section we use the solution of the time-dependent Schrödinger equation, that is the wave function, to show that a freely propagating rectangular wave packet exhibits the phenomenon of focusing. For this purpose we first express the time-dependent wave function in terms of a Fresnel integral, and then derive analytic approximations for the wave function as well as the probability density. To bring out most clearly the focusing effect we finally calculate the Gaussian width [5] of the wave packet and demonstrate that it exhibits a clear minimum at the time of the focusing.

3.1 Time evolution

Central to our discussion is the free propagation of a wave packet corresponding to a non-relativistic particle of mass M. The initial wave function

$$\begin{aligned} \psi _{0}(x) \equiv \psi (x, t=0) \equiv \frac{1}{\sqrt{L}} \varTheta \left( \frac{L}{2}-|x|\right) \end{aligned}$$

(1)

is of rectangular form with a length L. Here $\varTheta$ denotes the Heaviside step function.

With the help of the propagator [74]

$$\begin{aligned} G(x, t|y, 0) \equiv \sqrt{\frac{\alpha (t)}{i\pi }} {\rm e}^{i\alpha (t)(x - y)^{2}} \end{aligned}$$

(2)

of a free particle connecting the initial coordinate y with x at time t, and the abbreviation

$$\begin{aligned} \alpha (t) \equiv \frac{M}{2\hbar t} \end{aligned}$$

(3)

containing the reduced Planck constant $\hbar$, we find from the Huygens principle of matter waves

$$\begin{aligned} \psi (x,t) = \int _{-\infty }^{\infty } {\rm d}y\, G(x, t|y, 0) \psi _{0}(y) \end{aligned}$$

(4)

the expression

$$\begin{aligned} \psi (x,t) = \sqrt{\frac{1}{i\pi L}} \int _{\sqrt{\alpha (t)}(x -L/2)}^{\sqrt{\alpha (t)}(x + L/2)} {\rm d}\xi \, {\rm e}^{i \xi ^{2}} , \end{aligned}$$

(5)

for the time-dependent probability amplitude. Here we have introduced the integration variable $\xi \equiv \alpha ^{1/2}(x - y)$.

When we decompose the integral in Eq. 5 into two parts each starting from $x=0$, the wave function

$$\begin{aligned} \psi (x,t)&= \sqrt{\frac{1}{2 i L}} \left\{ F\left[ \sqrt{\alpha (t)}(x + L/2)\right] \right. \nonumber \\&\quad \left. - F\left[ \sqrt{\alpha (t)}(x - L/2)\right] \right\} \end{aligned}$$

(6)

consisting of the difference of two Fresnel integrals

$$\begin{aligned} F(w) = \sqrt{\frac{2}{\pi }} \int _{0}^{w} {\rm d}\xi \, {\rm e}^{i \xi ^{2}} , \end{aligned}$$

(7)

is thus determined by the interference of the diffraction patterns originating from two semi-infinite walls located at $x=L/2$ and $x=-L/2$. The amplitude and phase of each contribution are given by the Fresnel integral F, whose real and imaginary parts

$$\begin{aligned} C(w) \equiv \sqrt{\frac{2}{\pi }}\int _{0}^{w} {\rm d}\xi \, \cos \xi ^2 \end{aligned}$$

(8)

and

$$\begin{aligned} S(w) \equiv \sqrt{\frac{2}{\pi }}\int _{0}^{w} {\rm d}\xi \, \sin \xi ^2 \end{aligned}$$

(9)

follow from the Cornu spiral [75] represented in the complex plane.¹

Fig. 1

Time evolution of a rectangular wave packet represented by its probability density $|\psi (x,t)|^{2}$, given by Eq. 5, depicted in continuous space-time (top) and at specific times (bottom) corresponding to a strongly oscillatory behavior, the focus, and the ballistic expansion. To bring out the characteristic features in the early-time evolution we have represented the time axis by a logarithmic scale. For a better comparison the initial wave packet at $t = 0$, that is for $\log (t = 0) = -\infty$ is moved to $\log (t) = -3.0$ since our time axis extends only to this value

In Fig. 1 we present the probability density $|\psi (x,t)|^{2}$ as a function of space and time. Here and in the remainder of our article we represent the coordinate x in units of L and the time t in units of the characteristic time

$$\begin{aligned} T \equiv \frac{M L^{2}}{2\pi \hbar } \equiv \frac{M L^{2}}{h} \end{aligned}$$

(10)

The curious inclusion of the factor $2\pi$ is motivated by the asymptotic expressions of $|\psi |^{2}$ discussed in the appendices. Moreover, the probability density $|\psi |^{2}$ is always in units of 1 / L.

Whereas on the top of Fig. 1 we show $|\psi (x,t)|^{2}$ in continuous space-time in the bottom panel we select specific time slices corresponding to (1) short times where the probability distribution oscillates strongly, (2) intermediate times leading to focusing, and (3) longer times representing the ballistic regime.

At $t = 0$ the probability density starts from its initial rectangular shape and immediately develops two peaks at the edges decorated with fringes. However, after this transitional phase the two peaks disappear and a dominant maximum at the origin $x = 0$ forms. It is most pronounced at $t \approx 0.342$ corresponding to the focus when the width of the wave packet assumes a minimum. Indeed, here the probability density assumes a maximum, which is about a factor 1.8 larger then at $t = 0$ where it is unity. After the focus, that is for larger times, the wave packet displays the familiar spreading effect.

3.2 Analytic approximations

Next we give approximate but analytical expressions for the time-dependent probability amplitude and probability density. Since our interest is to obtain the behavior at early times, that is before the ballistic expansion occurs, we shall consider small values of t, corresponding to the regime where $\alpha (t)$ is large.

With the help of the asymptotic expansion [76]

$$\begin{aligned} \int _{0}^{a} {\rm d}\xi \, {\rm e}^{i \xi ^{2}} \cong \frac{\sqrt{i\pi }}{2} + \frac{{\rm e}^{ia^{2}}}{2i a} \end{aligned}$$

(11)

valid for $1 \ll a$ the expression Eq. 5 for the probability amplitude reduces to

$$\begin{aligned} \psi (x,t)&\cong \frac{1}{\sqrt{i \pi L}} \left[ \sqrt{i \pi } + \frac{{\rm e}^{i\alpha (t)(L/2-x)^2}}{2i\sqrt{\alpha (t)}(L/2-x)} \right. \nonumber \\&\quad + \left. \frac{{\rm e}^{i\alpha (t)(L/2+x)^2}}{2i\sqrt{\alpha (t)}(L/2+x)} \right] , \end{aligned}$$

(12)

and the probability density reads

$$\begin{aligned} |\psi (x,t)|^2&\cong \frac{1}{L\pi } \left| \left[ \sqrt{i\pi } + \frac{{\rm e}^{i\alpha (t)(L/2-x)^2}}{2i\sqrt{\alpha (t)}(L/2-x)} \right. \right. \nonumber \\&\quad + \left. \left. \frac{{\rm e}^{i\alpha (t)(L/2+x)^2}}{2i\sqrt{\alpha (t)}(L/2+x)} \right] \right| ^{2} . \end{aligned}$$

(13)

This expression simplifies further when we neglect terms $\mathcal {O}\left[ t^{2}/(1 \pm 2x/L)^{2}\right]$ and takes the form

$$\begin{aligned} |\psi (x,t)|^2&\cong \frac{1}{L} \left[ 1 + \frac{ \sin \left[ \alpha (t)(L/2-x)^2 -\pi /4 \right] }{\sqrt{ \pi \alpha (t)}(L/2-x)} \right. \nonumber \\&\quad + \left. \frac{\sin \left[ \alpha (t)(L/2+x)^2 - \pi /4 \right] }{\sqrt{ \pi \alpha (t)}(L/2+x)} \right] . \end{aligned}$$

(14)

In Fig. 2 we compare and contrast the resulting probability densities at $x = 0$ as a function of time and find excellent agreement between the numerical result following from the evaluation of the integral of Eq. 5, and the approximations based on Eqs. 13 and 14. We emphasize that our approximations break down for very large values of t, but they succeed in giving the maximum of the distribution corresponding to the focusing effect.

We also test in Fig. 3 our approximate but analytic expressions, Eqs. 13 and 14, for the probability density against the exact numerical result given by Eq. 5 at characteristic times confirming again the focusing effect.

Fig. 2

Comparison between the exact numerical (red) and two approximate analytical expressions (blue and green) for the probability density $|\psi (x=0,t)|^{2}$ as a function of time. Our curves are based on Eqs. 5, 13 and 14, respectively. The oscillations near $t = 0$ are well approximated both in amplitude and phase by the blue and green curves. A maximum occurs for $t \approx 0.342$. Both approximations fail for large times

Fig. 3

Comparison between the exact numerical position-dependent probability density (red) given by Eq. 5 with the approximate formulae (blue and green) represented by Eqs. 13 and 14, respectively. In the four panels the axes cover identical domains

3.3 Focusing expressed by the Gaussian width

So far we have analyzed the phenomenon of diffractive focusing of our rectangular wave packet by considering the complete probability density in space and time. We now characterize this effect by the Gaussian measure [5]

$$\begin{aligned} \delta x^{2}(t) \equiv \frac{1}{\kappa ^2}\left[ 1- \int _{-\infty }^{\infty } {\rm d}x\, {\rm e}^{-(\kappa x)^2} |\psi (x,t)|^2 \right] \end{aligned}$$

(15)

discussed in more detail in “Appendix A”. Here $\kappa$ is a constant with units of an inverse length.

For our rectangular wave packet we obtain the Gaussian width by numerically evaluating Eq. 15 using the integral representation Eq. 5 of the probability amplitude. In Fig. 4 we depict the corresponding curve normalized to its initial value $\delta x^{2}(0)$ for $\kappa = 6.0$ which displays a clear minimum at $t \approx 0.39$, thus confirming the focusing effect.

However, we note that the location of the minimum of $\delta x^{2} = \delta x^{2}(t)$ deviates slightly from the location of the maximum of $|\psi (x=0, t)|^{2}$ which occurs at $t = 0.342$ as indicated in Fig. 2. This deviation is the result of the integration in Eq. 15.

4 Experimental approach

In the preceding section we have shown that a rectangular matter wave packet first focuses before it spreads. We now describe an experiment to observe the diffraction pattern and, in particular, the focusing arising close to the slit. Here we take advantage of the familiar analogy between the Schrödinger equation

$$\begin{aligned} i \hbar \frac{\partial \psi }{\partial t} = -\frac{\hbar ^{2}}{2 M}\,\frac{\partial ^{2} \psi }{\partial x^{2}} \end{aligned}$$

(16)

of a free particle, and the paraxial wave equation

$$\begin{aligned} 2i k \frac{\partial \psi }{\partial z} = -\frac{\partial ^{2} \psi }{\partial x^{2}} \end{aligned}$$

(17)

of classical optics. In this situation z denotes the coordinate of propagation and k the wave vector of the electromagnetic wave.

Indeed, the two wave equations are identical when we make the substitution

$$\begin{aligned} z \equiv \frac{\hbar k}{M} t = \frac{2\pi \hbar }{M L^{2}}\frac{L}{\lambda } L t = \frac{L}{\lambda } L \frac{t}{T} \end{aligned}$$

(18)

where $\lambda$ is the wave length. In the last step we have recalled the definition, Eq. 10 of the characteristic time T. Hence, time in the Schrödinger equation translates into propagation distance z.

As a consequence of the analogy between Eqs. 16 and 17 with the scaling given by Eq. 18, it suffices to perform our experiment with light rather than matter waves.

4.1 Setup

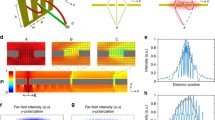
We use a confocal microscope for measuring the light intensity diffracted by a one-dimensional slit milled in an aluminum film.² The slit of length 50 $\upmu$m and width 2440 nm is illuminated by laser light of wavelength 488 nm as shown in Fig. 5a. A single mode optical fiber with collimator was used for the illumination. The collimated laser beam has a diameter of approximately 1 mm and is, therefore, much larger than the slit. For this reason we assume the illumination of the slit as a plane wave.

To generate images in different planes above the slit we employ a confocal laser scanning microscope (WITec GmbH). The objective used for light collection was an infinitely corrected Olympus MPlan with 100$\times$ magnification and numerical aperture NA = 0.9. The collected light was focused into a multimode optical fiber connected to an avalanche photodiode. The light diffracted by the slit is measured in a rasterized way. Each point corresponds to a pixel of an image generated by scanning in the horizontal, or in the vertical direction, as outlined in Fig. 5a.

4.2 Results

In Fig. 5b, c, we present images of the light intensity in the plane of the slit, and perpendicular to the sample, respectively. In the latter case, we scan the confocal microscope in the vertical direction with a minimum scan step of $\Delta z \approx 50$ nm. The pixel size in the horizontal direction corresponds to a dislocation of $\Delta x = \Delta y = 10 \ \upmu {\rm m} / 512 \text {--} 20$ nm. Thus, each pixel is much smaller than the wavelength and the optical resolution, which according to the Rayleigh criterion is $\Delta r \equiv 0.61\times \lambda / {\rm NA}$. The horizontal fringes appearing in the light intensity of Fig. 5c are due to the mechanical motion of the microscope when scanning vertically the diffracted light. We note the dominant maximum of the intensity at $z \approx 4.1$ $\upmu$m which confirms our prediction of the focusing effect.

To analyze the phenomenon in a quantitative way we use the experimental intensity distribution of Fig 5c to obtain the Gaussian width $\delta x^{2}$ defined by Eq. 15. The so-calculated curve, now displayed in Fig. 4 as a function of the propagation distance z and scaled according to Eq. 18, follows nicely the theoretical prediction. In particular, it displays the characteristic minimum indicating focusing at the same location as the theoretical curve.

The rapid modulation of the experimental curve is a consequence of the horizontal fringes emerging due to the mechanical motion of the microscope as mentioned above, and thus of the measurement technique. An average over these oscillations leads to a smooth curve following the theoretical curve.

Fig. 4

Comparison between the numerical and experimental Gaussian width $\delta x^{2}(t)/\delta x^{2}(0)$ of a focusing rectangular wave packet. To have the same domain in the abscissa the z-coordinate of the experimental data (blue curve) was scaled using $L = 2.44$ $\upmu$ m. The time coordinate t of the theoretical evaluation (green curve) based on Eq. 5 was scaled according to Eq. 18 with $\lambda = 0.2$. For both curves we have chosen $\kappa = 6.0$

Fig. 5

Experimental verification of diffractive focusing from a single slit: setup (a) based on a confocal microscope viewing a section of the slit, and light intensity measured in the $x-y$ plane of the slit (b), and in the $x-z$ plane perpendicular to the substrate and slit (c)

4.3 Paraxial versus non-paraxial optics

To compare our experimental results to the theoretical predictions of classical optics we have calculated the intensity and phase for a slit of width $L = 2.44$ $\upmu$m illuminated by light of wave length $\lambda = 0.488$ $\upmu$m corresponding to the same ratio $L/\lambda = 5$ as in the experiment. For this purpose we use the Fresnel and the Rayleigh–Sommerfeld diffraction integrals familiar from paraxial and non-paraxial optics, respectively. In particular, we have chosen the Rayleigh–Sommerfeld integral of the first kind (RS-I) [4, 12, 13]³ and made use of numerical integration and algorithms reported in [77]⁴.

In Fig. 6a, b we depict the intensities following from the Rayleigh–Sommerfeld and Fresnel integrals, respectively. Moreover, in Fig. 7a, b we show the corresponding phases. For a direct comparison with Fig. 5 we have refrained from using normalized coordinates for both axis.

We note three characteristic features: (1) the number of intensity lobes is finite for RS-I, whereas it is infinite for Fresnel. (2) The phase pattern predicted by RS-I evolves almost as a plane wave in the propagation direction. In contrast, the Fresnel phase shows small oscillations around zero radians in the propagation direction, but rapid oscillations in the transverse direction, and (3) the Fresnel and RS-I intensity tend to agree as we move away from the slit. In particular, the focus occurs approximately in the same position for both calculations, as we show later.

We conclude this section by noting that although RS-I is only valid for scalar waves its intensity map still fits well with the optical intensity obtained experimentally.

Fig. 6

Comparison of the intensities of a plane wave of wave length $\lambda = 0.488$ $\upmu$m diffracted by a slit of width $L = 2.44$ $\upmu$m calculated either from the Rayleigh–Sommerfeld integral RS-I (a), or the Fresnel integral (b). In both cases focusing occurs at $z \approx 4$, where the intensity reaches the value of 1.8. However, in contrast to the Fresnel diffraction the number of lobes for the RS-I diffraction is finite

Fig. 7

Comparison of the phase patterns of a plane wave of wavelength $\lambda = 0.488$ $\upmu$m diffracted by a slit of width $L = 2.44$ $\upmu$m calculated either from the Rayleigh–Sommerfeld integral RS-I (a), or the Fresnel integral (b). The wavefronts for the non-paraxial case evolve in the forward direction almost parallel with small perturbations. However, the paraxial phase shows a much more complicated behavior with small fluctuations around zero radians on the optical axis and rapid oscillations in the lateral direction close to the slit

5 Wigner function approach

In the preceding sections we have analyzed the focusing of a rectangular wave packet with the help of the time-dependent Schrödinger equation and have confirmed the effect using optical waves. We now consider this phenomenon from a different point of view, that is from phase space taking advantage of the Wigner function. This formalism has the remarkable feature that the time evolution is identical to the classical one, consisting of a shearing of the initial Wigner function. The latter contains the interference nature of quantum mechanics.

5.1 Probability density from tomographic cuts

The Wigner function has several unique properties. The ones most relevant for the present discussion are: (1) the time evolution of a free particle follows by a replacement of the phase space variables according to the classical motion, and (2) the corresponding probability densities originate from the integration of the Wigner function over the conjugate variable, that is by an appropriate tomographic cut. We now discuss these features in more detail and derive an expression for the probability density which is different from, but equivalent to the one discussed in Sect. 2.

5.1.1 A brief introduction

Wigner functions are quasi-probability distributions first introduced by Wigner [52] in the context of quantum correlations in statistical mechanics. They belong to the Cohen class of distributions [66] and are, therefore, related to other quadratic kernel distributions.

There exist extensive applications of the Wigner function, not only in quantum physics, but also in optics and signal processing [57, 87]. Indeed, Wigner functions are frequently used to represent quantum systems in phase space [60, 62, 88, 89]. Moreover, they describe the time evolution of wave packets in a similar way as classical phase space distributions in terms of the trajectories of classical particles [63] and have also been used in the study of diffraction in time of wave packets [51, 61, 90], a topic that has been addressed several times since the seminal article of Moshinsky [8].

5.1.2 Definition and time evolution

In this section we first define the Wigner function and discuss its time evolution in phase space. We then use its property to provide us with the marginals to compute the time- and space-dependent probability density. Here we take advantage of the fact that the Wigner function at arbitrary times is easy to obtain [63].

Indeed, for a given wave function $\psi = \psi (x)$ we find the corresponding Wigner function from the definition

$$\begin{aligned} W(x,p) \equiv \mathcal {N} \int _{-\infty }^{\infty } {\rm d}\xi \, {\rm e}^{i p \xi / \hbar } \psi \left( x-{\textstyle {1\over 2}}\xi \right) \psi ^{*}\left( x+{\textstyle {1\over 2}}\xi \right) \end{aligned}$$

(19)

with the normalization factor $\mathcal {N} \equiv 1/(2 \pi \hbar )$, and a free particle undergoing time evolution is described in phase space by the time-dependent Wigner function

$$\begin{aligned} W(x,p;t) = W_0 \left( x-\frac{pt}{M}, p\right) . \end{aligned}$$

(20)

Here $W_{0} \equiv W(x,p; t = 0)$ denotes the Wigner function of the initial wave function $\psi _{0} \equiv \psi (x,t=0)$.

The probability density

$$\begin{aligned} |\psi (x,t)|^2 = \int _{-\infty }^{\infty } {\rm d}p\, W_{0} \left( x - \frac{pt}{M}, p\right) \end{aligned}$$

(21)

at a given point in space and time is obtained by integration over p which after the change of variables $y \equiv x - (p/M)t$ reads

$$\begin{aligned} |\psi (x,t)|^2 = \frac{M}{t} \int _{-\infty }^{\infty } {\rm d}y\, W_0 \left( y, M(x-y)/t \right) . \end{aligned}$$

(22)

This representation is particularly useful in the discussion of the asymptotic behavior of the probability density addressed in more detail in “Appendix B”.

5.2 Time evolution: rectangular wave function

We are now in the position to consider the time evolution of our rectangular wave function. For this purpose we first calculate the Wigner function corresponding to this wave, and then analyze the shearing in phase space. Although we mainly study the motion of the complete Wigner function we also concentrate on those contributions in phase space which lead to the focusing.

5.2.1 General case

According to “Appendix B” the Wigner function of the rectangular wave packet, Eq. 1 reads

$$\begin{aligned} W_0(x,p) = \frac{1}{\pi L} \varTheta \left( \frac{L}{2} - |x| \right) \frac{1}{p}\sin \left[ \frac{p}{\hbar }(L - 2|x|)\right] \end{aligned}$$

(23)

and is shown in Fig. 8a. Here we identify three characteristic features: (1) since the rectangular wave function is restricted to the interval $|x| \le L/2$ also the Wigner function is limited in phase space to this domain. (2) The Wigner function assumes positive as well as negative values. (3) We recognize a dominant positive contribution along the x-axis with a maximum at the origin.

The time evolution given by Eq. 20 manifests itself in a shearing of the initial Wigner function $W_{0}$ shown in Figs. 8b, c. Indeed, every point (x, p) of the Wigner phase space moves according to the Newton law, that is $x \rightarrow x + p t/M$ while p is a constant of the motion.

Especially the Wigner function of Fig. 8c is interesting since it represents the moment of focusing. Indeed, by this time all negative contributions of W have moved away⁵ from the positive peak centered at the x-axis but now subtract from its wings. This fact stands out more clearly in the position distribution shown in Fig. 8d which can be understood as the result of an integration of W over the momentum variable.

Fig. 8

Time evolution of the Wigner function corresponding to a rectangular wave packet represented by three density plots illustrating the shearing in phase space together with the associated probability densities in position space. The Wigner function of the initially rectangular wave packet is depicted in a at $t = 0$. The distribution shears with time, as shown in b at time $t=0.0628$, and the moment of focussing c at $t = 0.342$. At the bottom d we display the corresponding probability densities in the coordinate x obtained by integration over the conjugate variable p. The momentum p is expressed in units of $\hbar /L$ as suggested by the argument of the sine function in the expression, Eq. 23, for the Wigner function

In this active approach the Wigner function evolves in time but the axes of phase space which define the tomographic cuts, that is integration over x or p remain fixed. An alternative formulation follows from Eq. 22. Here the Wigner function remains static, while the line of integration evolves in time according to $x + (p/M)t = 0$. In Fig. 9, we show the probability density at $x = 0$ as obtained from the Wigner function through integration from this passive point of view.

The cut at $t = 0$ runs along the momentum axis. Here the oscillations in the Wigner function $W_{0}$ along p average out and the main contribution to the probability density arises from the positive domain along the x-axis. For small times the lines of integration enclose small angles with respect to the p-axis and the oscillations in $W_{0}$ translate in an oscillatory probability density. A dominant maximum occurs when the cut feels the central positive ridge along the x-axis. The density decays for larger times, that is as the cut approaches the x-axis, since there is a decreasing overlap.

Fig. 9

Diffractive focusing of a rectangular wave packet explained from Wigner phase space. At the center we depict the Wigner function of the initial rectangular wave packet as a surface on top of the $x-p$ plane. The blue curve projected onto the surface of a cylinder represents the probability density $|\psi (0, t)|^2$, and is the result of an integration along the red lines $x + p t/M = 0$ at different times corresponding to different angles with respect to the $x-$axis. Clearly, the focusing occurs for a line sweeping only positive values of the Wigner function at the approximate time $t \approx 0.342$

5.2.2 Rays and envelopes

According to Eq. 20 each point in Wigner phase space follows its classical trajectory. Thus, the value of $W_{0}$ at $(x_{0},p_{0})$ will move from $x_{0}$ to

$$\begin{aligned} x = x_{0} + \frac{p_{0}}{M} t \end{aligned}$$

(24)

at time t. We now use these rays to show that the minima of the Wigner function generate the regions in space-time where the probability density $|\psi (x,t)|^{2}$ assumes small values as exemplified by Fig 10. Thus, they indicate the x values of the minima of $|\psi (x,t)|^{2}$ as the system evolves in time.

The explicit expression Eq. 23 for the initial Wigner function $W_{0}$ tells us that the minima of $W_{0}$ are given by the condition

$$\begin{aligned} \frac{p_{0}^{(n)}}{\hbar }(L-2|x_{0}|) = \pi \left( 2n + \frac{3}{2}\right) \end{aligned}$$

(25)

for p positive, and

$$\begin{aligned} \frac{p_{0}^{(n)}}{\hbar }(L - 2|x_{0}|) = -\pi \left( 2n + \frac{3}{2}\right) \end{aligned}$$

(26)

for p negative, with $n=0,1,2, \dots$

We substitute these expressions for $p_{0}^{(n)}$ into the motion, Eq. 24, and rearrange the terms, which yield

$$\begin{aligned} (x-x_{0})(L-2x_{0})\mp \left( 2n + \frac{3}{2}\right) \frac{\pi \hbar }{M}t = 0 \end{aligned}$$

(27)

for $x_{0}$ positive, and

$$\begin{aligned} (x-x_{0})(L+2x_{0})\mp \left( 2n + \frac{3}{2}\right) \frac{\pi \hbar }{M}t = 0 \end{aligned}$$

(28)

for $x_{0}$ negative. The upper signs in Eqs. 27 and 28 are for positive $p_{0}^{(n)}$, that is for a positive slope in the (x, t) plane, and the lower signs for negative $p_{0}^{(n)}$.

The envelope of a set of curves $F(x,t; x_{0}) = 0$, each determined by a parameter $x_{0}$, follows [91] from the requirements

$$\begin{aligned} \frac{\partial F}{\partial x_{0}} = 0 \quad \text {and} \quad F = 0 . \end{aligned}$$

(29)

We consider the two cases, $x_{0}>0$ and $x_{0}<0$ in turn.

For positive $x_{0}$, the first condition gives

$$\begin{aligned} x_{0}=\frac{L+2x}{4} , \end{aligned}$$

(30)

which, when substituted into Eq. 27, yields the relation

$$\begin{aligned} -\frac{1}{2}\left( \frac{L}{2} - x\right) ^{2} = \pm \left( 2n + \frac{3}{2}\right) \frac{\pi \hbar }{M}t . \end{aligned}$$

(31)

Thus, only negative values of $p_{0}^{(n)}$ contribute to this envelope and we obtain the space-time trajectories

$$\begin{aligned} t = \frac{(L/2-x)^{2}}{2n+3/2}\,\frac{M}{2\pi \hbar } \end{aligned}$$

(32)

of the minima.

According to this expression they are parabolas ⁶ emerging from $x = L/2$ with a steepness inversely proportional to $(2n + 3/2)$. Hence, the largest steepness corresponds to the case of $n = 0$ with the parabola crossing the t-axis, that is $x = 0$, at the time

$$\begin{aligned} t = \frac{1}{6}\frac{ML^{2}}{2\pi \hbar } = \frac{1}{6} T , \end{aligned}$$

(33)

where in the last step we have recalled the definition, Eq. 10 of the characteristic time T.

For negative $x_{0}$, the first condition in Eq. 29 provides us with the relation

$$\begin{aligned} x_{0}=-\frac{L - 2x}{4} , \end{aligned}$$

(34)

which, when substituted into Eq. 28, gives

$$\begin{aligned} \frac{1}{2}\left( \frac{L}{2} + x\right) ^{2} = \pm \left( 2n + \frac{3}{2}\right) \frac{\pi \hbar }{M}t . \end{aligned}$$

(35)

Since in this case only positive values of $p_{0}^{(n)}$ contribute to this envelope we arrive at the space-time trajectory

$$\begin{aligned} t = \frac{(L/2 + x)^{2}}{2n+3/2}\,\frac{M}{2\pi \hbar } \end{aligned}$$

(36)

corresponding to parabolas emerging from $x = - L/2$. They are the mirror image of the ones given by Eq. 32.

In Fig. 10 we present the envelopes, Eqs. 32 and 36, along with the corresponding probability density $|\psi (x,t)|^{2}.$ Hence, these minima coincide with the minima of the intensity pattern and are harbingers of the maxima and, in particular, of the focus.

Fig. 10

Probability density $|\psi (x,t)|^{2}$ represented in space-time and overlaid with the envelopes (gray lines) of the diffraction in time created by a rectangular wave packet of initial width $L = 1$. The time t has been scaled using the characteristic time T. Here the envelopes given by Eqs. 32 and 36 approximate well the motion of the minima of $|\psi (x,t)|^{2}$

6 Summary and outlook: beyond slits

The spreading of a wave packet in the absence of a potential is a well-known phenomenon in quantum physics. However, also the opposite effect, that is a focusing of the wave packet can be achieved. In this case we have to imprint an appropriate position-dependent phase onto the initial wave function. Is it possible to achieve focusing even in the absence of any phase factors, that is for a real-valued initial wave function?

In the present article we have provided such an example in the form of a rectangular wave packet and have illuminated the resulting focusing in position as well as in phase space. Here we have used the time-dependent wave function and the Wigner distribution. Moreover, we have confirmed this phenomenon using laser light being diffracted from a slit building on the analogy between classical Fresnel optics and Schrödinger wave mechanics.

Throughout our article we have concentrated on rectangular wave packets created by a slit, that is by a one-dimensional aperture. However, similar effects appear in the diffraction from a two-dimensional aperture. In “Appendix C” we briefly summarize the literature on this problem, and discuss the similarities and differences between the one- and two-dimensional case using the examples of a slit and a circular aperture.

Figures 11 and 12 bring out most clearly the characteristic features of this dependence on the number of dimensions: (1) for the slit the relative intensity at the focus reaches the value of 1.8, whereas for the circular aperture the maximum is 4.0. (2) The position of the focus in the case of the circular aperture is closer to the opaque screen than in the slit, and (3) the focus originating from a circular aperture is more confined, since its decay towards the far-field region is faster.

This analysis shows that in two dimensions the focusing effect is more pronounced. Moreover, it is possible to optimize this effect by choosing different apertures, either by appropriate apodization, or by creating an optimal wave packet. Unfortunately, this topic goes beyond the scope of the present article and has to be postponed to a future publication.

Fig. 11

Rayleigh–Sommerfeld intensity pattern for a slit of width $L = 5\lambda$ and illumination wave length $\lambda = 0.488$ $\upmu$m (a), together with a comparison between the on-axis intensities predicted by the Rayleigh–Sommerfeld and Fresnel integrals (b). In contrast to Figs. 5, 6 and 7 the horizontal axes are normalized

Fig. 12

Rayleigh–Sommerfeld intensity pattern for a circular aperture of diameter $L = 2 a = 5\lambda$ and illumination wavelength $\lambda = 0.488$ $\upmu$m (a), together with a comparison between the on-axis intensities predicted by the Rayleigh–Sommerfeld and Fresnel integrals (b). Again the axes are normalized

Appendices

Appendix A: Gaussian width

In this appendix we summarize the evaluation of the time-dependent Gaussian width defined by Eq. 15 of our rectangular wave packet. To gain some insight into this unusual definition of width we first discuss several of its general properties and then rederive the familiar spreading of a Gaussian wave packet undergoing free expansion employing this measure. We conclude by considering the case of the rectangular wave packet.

1.1 A.1: General properties

We start our discussion of the Gaussian width

$$\begin{aligned} \delta x^{2} \equiv \frac{1}{\kappa ^{2}}\left[ 1 - \langle {\rm e}^{-(\kappa x)^{2}}\rangle \right] \end{aligned}$$

(37)

of the probability density $P = P(x)$ with the average

$$\begin{aligned} \langle {\rm e}^{-(\kappa x)^{2}}\rangle \equiv \int _{-\infty }^{\infty } {\rm d}x\,{\rm e}^{-(\kappa x)^{2}}\, P(x) \end{aligned}$$

(38)

by noting that for $\kappa \rightarrow 0$ the familiar expansion

$$\begin{aligned} {\rm e}^{-(\kappa x)^{2}} \cong 1 - (\kappa x)^{2} \end{aligned}$$

(39)

leads us to

$$\begin{aligned} \delta x^{2} \cong \langle x^{2} \rangle . \end{aligned}$$

(40)

Hence, in this limit the Gaussian width $\delta x^{2}$ reduces to the second moment $\langle x^{2} \rangle$ of $P = P(x)$.

Whenever P displays oscillations in the position variable x around an average value $\overline{P}$ that are rapid on the decay length $1/\kappa$ of the Gaussian in the definition, Eq. 37, of $\delta x^{2}$ the oscillatory part averages out, and the familiar integral relation

$$\begin{aligned} \int _{-\infty }^{\infty } {\rm d}\xi \, {\rm e}^{-\gamma \xi ^{2}} = \sqrt{\frac{\pi }{\gamma }} \end{aligned}$$

(41)

yields

$$\begin{aligned} \delta x^{2} \cong \frac{1}{\kappa ^{2}}\left[ 1 - \frac{\sqrt{\pi }}{\kappa }\overline{P} \right] . \end{aligned}$$

(42)

The other extreme occurs when $P=P(x)$ is slowly varying compared to $\exp [-(\kappa x)^{2}]$. In this case we can evaluate P at $x = 0$, factor it out of the integral and perform the integral with the help of Eq. 41. Thus, we arrive at the approximate expression

$$\begin{aligned} \delta x^{2} \cong \frac{1}{\kappa ^{2}}\left[ 1 - \frac{\sqrt{\pi }}{\kappa }P(x=0) \right] , \end{aligned}$$

(43)

which implies that the dependence of $\delta x^{2}$ on an additional parameter, such as time is governed by the dependence of the probability density P at the origin on that parameter.

Obviously, the most interesting case emerges when P and $\exp \left[ -(\kappa x)^{2}\right]$ vary on approximately the same length scale. This situation is of special interest when P exhibits a dominant maximum at $x = 0$. Indeed, with the help of the Taylor expansion

$$\begin{aligned} P(x) \cong P(0) - \frac{1}{2}\left| P^{\prime \prime }(0)\right| x^{2} \end{aligned}$$

(44)

around this point we find from the identity

$$\begin{aligned} P(x) = \exp \left\{ \ln \left[ P(x) \right] \right\} \end{aligned}$$

(45)

the Gaussian approximation

$$\begin{aligned} P(x) \cong P(0)\exp \left[ -\frac{1}{2}\frac{|P^{\prime \prime }(0)|}{P(0)}x^{2}\right] \end{aligned}$$

(46)

of P. Here prime denotes differentiation with respect to x.

As a result, we obtain the expression

$$\begin{aligned} \delta x^{2} \cong \frac{1}{\kappa ^{2}}\left[ 1 - \frac{\sqrt{\pi } P(0)}{\sqrt{\kappa ^{2} + \frac{\displaystyle |P^{\prime \prime }(0)|}{\displaystyle 2 P(0)}}} \right] , \end{aligned}$$

(47)

where we have used again the integral relation, Eq. 41.

1.2 A.2: Gaussian wave packet

Next we evaluate the Gaussian width for a freely spreading Gaussian wave packet of initial form

$$\begin{aligned} \psi _0(x) \equiv \mathcal {N} {\rm e}^{-\beta x^2} \end{aligned}$$

(48)

with $\mathcal {N} \equiv (2 \beta /\pi )^{1/4}$ and a real-valued constant $\beta$.

From the Huygens integral, Eq. 4, together with the propagator, Eq. 2, we obtain with the help of the integral relation

$$\begin{aligned} \int _{-\infty }^{\infty } {\rm d}\xi \, {\rm e}^{-\gamma \xi ^{2} + 2\sigma \xi } = \sqrt{\frac{\pi }{\gamma }}\, {\rm e}^{\sigma ^{2}/\gamma } \end{aligned}$$

(49)

the wave function

$$\begin{aligned} \psi = \mathcal {N} \sqrt{\frac{\alpha }{\alpha + i\beta }} \exp \left( i \frac{\alpha \beta }{\beta - i\alpha } x^{2} \right) , \end{aligned}$$

(50)

and thus the probability density

$$\begin{aligned} |\psi |^{2} = \mathcal {N}^{2} \frac{\alpha }{\sqrt{\alpha ^{2} + \beta ^{2}}} \exp \left( -2 \frac{\alpha ^{2}\beta }{\alpha ^{2} + \beta ^{2}} x^{2} \right) . \end{aligned}$$

(51)

When we now substitute this expression into the definition, Eq. 37 of the Gaussian measure $\delta x^{2}$ of width and recall the identity, Eq. 41, we arrive at the result

$$\begin{aligned} \delta x^{2} = \frac{1}{\kappa ^{2}}\left[ 1 - \sqrt{\frac{2\alpha ^{2}\beta }{\kappa ^{2}(\alpha ^{2} + \beta ^{2}) + 2\alpha ^{2}\beta }} \right] , \end{aligned}$$

(52)

or

$$\begin{aligned} \delta x^{2} = \frac{1}{\kappa ^{2}}\left( 1 - \left\{ 1 + \frac{\kappa ^{2}}{2\beta }\left[ 1 + \left( \frac{\beta }{\alpha }\right) ^{2} \right] \right\} ^{-1/2} \right) . \end{aligned}$$

(53)

We note that for $\kappa ^{2}/(2\beta ) \ll 1$ and $(\beta /\alpha )^{2} < 1$ corresponding to early times this expression reduces to

$$\begin{aligned} \delta x^{2} \cong \frac{1}{4\beta }\left[ 1 + \left( \frac{\beta }{\alpha }\right) ^{2} \right] , \end{aligned}$$

(54)

that is to the second moment $\langle x^{2} \rangle$ of the Gaussian, Eq. 51, as predicted by Eq. 40.

Even more interesting is the limit $1 \ll (\beta /\alpha )^{2}$ corresponding to large times where Eq. 53 takes the form

$$\begin{aligned} \delta x^{2} \cong \frac{1}{\kappa ^{2}}\left[ 1 - \sqrt{\frac{2}{\beta }}\frac{\alpha (t)}{\kappa }\right] . \end{aligned}$$

(55)

According to the definition, Eq. 3, of $\alpha$ we find $\alpha \propto 1/t$ and thus $\delta x^{2}$ increases in a monotonic way tending towards the constant $1/\kappa ^{2}$. This time dependence of the Gaussian width is in sharp contrast to the one of the second moment $x^{2}$ given by Eq. 54 which increases quadratically with time without a bound.

1.3 A.3: Rectangular wave packet

Finally we turn to the Gaussian width $\delta x^{2}$ of the rectangular wave packet. Here we use the approximations developed in Sect. A.1 together with the properties of the approximate expressions, Eqs. 14 and 89 for the probability density $P(x,t) = |\psi (x,t)|^{2}$.

Indeed, for early times Eq. 14 predicts rapid oscillations around $\overline{P} = 1/L$ due to the fact that $\alpha$, which according to Eq. 3 is inversely proportional to t, is large. Hence, we find from Eq. 42 the approximation

$$\begin{aligned} \delta x^{2} \cong \frac{1}{\kappa ^{2}}\left( 1 - \frac{\sqrt{\pi }}{\kappa L} \right) . \end{aligned}$$

(56)

In the other extreme, that is for large times Fig. 1 shows that P is slowly varying. As a result, we obtain from Eq. 43 the formula

$$\begin{aligned} \delta x^{2}(t) \cong \frac{1}{\kappa ^{2}}\left[ 1 - \frac{\sqrt{\pi }}{\kappa }|\psi (x=0,t)|^{2} \right] , \end{aligned}$$

(57)

and the time dependence of $\delta x^{2}$ is determined by the one of the probability density at the origin. Hence, a maximum in $|\psi (x=0,t)|^{2}$ translates into a minimum of $\delta x^{2}$ and vice versa.

However, in the neighborhood of the focus it is necessary to use the approximation Eq. 47 which requires P(0) and $P^{\prime \prime }(0)$. According to Fig. 3 the expression for P, Eq. 14, approximates well the exact distribution. Therefore, it suffices to expand Eq. 14 up to the second order in x and we find

$$\begin{aligned} P(0,t) = \frac{1}{L} \left[ 1 + 4 \sqrt{\frac{2\hbar t}{\pi M L^{2}}} \sin \left( \frac{M L^{2}}{8 \hbar t}-\frac{\pi }{4} \right) \right] \end{aligned}$$

(58)

and

$$\begin{aligned} P^{\prime \prime }(0,t)&= \frac{32}{L^{3}}\sqrt{\frac{2\hbar t}{\pi M L^{2}}}\left\{ \left[ 2\left( \frac{M L^{2}}{8\hbar t}\right) ^{2} - 1\right] \right. \nonumber \\&\quad \times \sin \left( \frac{M L^{2}}{8\hbar t} - \frac{\pi }{4}\right) \nonumber \\&\quad + \left. \frac{M L^{2}}{8\hbar t}\cos \left( \frac{M L^{2}}{8\hbar t} - \frac{\pi }{4}\right) \right\} . \end{aligned}$$

(59)

In Fig. 13 we compare and contrast the three approximations Eqs. 56,  57, and 47 together with 58 and 59 to the numerically obtained curve based on the Fresnel integral, Eq. 5. We note that Eq. 56 provides us with the correct starting point of $\delta x^{2}$. Moreover, when we use Eq. 89 for $|\psi (x=0,t)|^{2}$ the approximation Eq. 57 describes well the long-time behavior but breaks down for short times. It is slightly off close to the focus. Here, only Eq. 47 together with Eqs. 58 and 59 yields a good fit to the exact curve.

Fig. 13

Comparison of the numerically obtained Gaussian width $\delta x^{2}$ as a function of time for the freely spreading rectangular wave packet (green curve), and its approximations for early and large times given by Eqs. 56 and 57 and depicted by blue and red curves, respectively, together with the Gaussian approximation, Eq. 47, around the focus using Eqs. 58 and 59. Here we have chosen the value $\kappa = 6.0$ as in Fig. 4. Equation 57 was evaluated using the approximation for large times, Eq. 89. In the graphic representation of Eq. 47 we have used Eqs. 58 and  59

Appendix B: Wigner dynamics of rectangular wave packet

In this appendix we analyze the time evolution of the rectangular wave packet from the point of view of Wigner phase space. For this purpose we first rederive the Wigner function of the initial rectangular wave packet and then obtain by integration over the momentum variable the time-dependent probability density in position space. The resulting integral representation for the probability density at $x = 0$ allows us to derive analytical approximations in three different time domains: (1) early and intermediate times, (2) around the focus, and (3) very long times. We conclude by presenting an exact expression as well as several approximations for the location of the focus.

1.1 B.1: Initial Wigner function

We start by computing the Wigner function

$$\begin{aligned} W_0(x,p) \equiv \mathcal {N} \int _{-\infty }^{\infty } {\rm d}\xi \, {\rm e}^{i p \xi /\hbar } \psi _{0}\left( x - {\textstyle {1\over 2}}\xi \right) \psi _{0}^{*}\left( x + {\textstyle {1\over 2}}\xi \right) \end{aligned}$$

(60)

with the normalization constant $\mathcal {N} \equiv 1/(2 \pi \hbar )$ for the square packet given by the wave function

$$\begin{aligned} \psi _{0}(x) \equiv \frac{1}{\sqrt{L}}\varTheta \left( \frac{1}{2}L - |x|\right) . \end{aligned}$$

(61)

When we substitute this expression into the definition of $W_{0},$ Eq. 60, we find

$$\begin{aligned} W_0(x,p)&= \frac{\mathcal {N}}{L} \int _{-\infty }^{\infty } {\rm d}\xi \, {\rm e}^{i p \xi / \hbar } \nonumber \\&\quad \times \varTheta \left( {\textstyle {1\over 2}}L-|x-{\textstyle {1\over 2}}\xi |\right) \, \varTheta \left( {\textstyle {1\over 2}}L-|x+{\textstyle {1\over 2}}\xi |\right) . \end{aligned}$$

(62)

The step functions imply the inequalities $-\frac{L}{2}< x - \frac{\xi }{2} < \frac{L}{2}$ and $-\frac{L}{2}< x + \frac{\xi }{2} < \frac{L}{2}$, which can be expressed as $-L + 2x< \xi < L + 2x$ and $-L - 2x< \xi < L - 2x$, leading us to the relation $-L + 2|x|< \xi < L - 2|x|$. These boundaries establish the limits of integration. Indeed, the integral vanishes for $2|x|-L \ge L-2|x|$ giving rise to a factor $\varTheta (L-2|x|)$.

Hence, the Wigner function corresponding to the rectangular wave packet reads

$$\begin{aligned} W_{0} = \frac{\mathcal {N}}{L} \int _{-L + 2|x|}^{L - 2|x|} {\rm d}\xi \, {\rm e}^{i p \xi /\hbar } \varTheta (L-2|x|) , \end{aligned}$$

(63)

which after integration takes the form

$$\begin{aligned} W_{0}(x, p) = \frac{1}{\pi L} \varTheta \left( \frac{L}{2} -|x|\right) \frac{1}{p} \sin \left[ (L - 2|x|) \frac{p}{\hbar } \right] , \end{aligned}$$

(64)

and is shown in Fig. 9.

1.2 B.2: Time-dependent probability density

Next we derive the time-dependent probability density $|\psi (x,t)|^{2}$ by integrating the time-dependent Wigner function

$$\begin{aligned} W(x,p;t) \equiv W_{0}\left( x - \frac{p}{M}t, p\right) \end{aligned}$$

(65)

over p, using the form

$$\begin{aligned} |\psi (x,t)|^2 = \frac{M}{t} \int _{-\infty }^{\infty } {\rm d}y\, W_0 \left[ y, \frac{M(x-y)}{t} \right] . \end{aligned}$$

(66)

When we substitute the expression Eq. 64 for $W_{0}$ with the appropriate arguments into Eq. 66 we arrive at the integral

$$\begin{aligned} |\psi (x,t)|^2&= \frac{1}{\pi L} \int _{-\infty }^{\infty } {\rm d}y\, \varTheta \left( \frac{L}{2} - |y|\right) \nonumber \\&\quad \times \frac{\sin \left[ (L - 2|y|) M (x - y) / (\hbar t) \right] }{x - y} , \end{aligned}$$

(67)

which reduces with the help of the Heaviside step function to

$$\begin{aligned} |\psi (x,t)|^2&= \frac{1}{\pi L } \int _{-L/2}^{L/2} {\rm d}y\, \frac{1}{x - y} \nonumber \\&\quad \times \sin \left[ \frac{ M L^2 }{\hbar t} \left( \frac{x-y}{L} \right) \left( 1 - 2\left| \frac{y}{L}\right| \right) \right] \end{aligned}$$

(68)

We conclude by introducing the abbreviation

$$\begin{aligned} \tau (t) \equiv \frac{\hbar t}{M L^{2}} \end{aligned}$$

(69)

and the change of variable $\eta \equiv 2y/L$ and arrive at the exact expression

$$\begin{aligned} |\psi (x,t)|^{2}&= \frac{1}{\pi L} \int _{-1}^{1} {\rm d}\eta \, \frac{1}{2 x / L - \eta } \nonumber \\&\quad \times \sin \left[ \frac{1}{2 \tau (t)} \left( \frac{2x}{L} - \eta \right) (1 - |\eta |) \right] \end{aligned}$$

(70)

for the time-dependent probability density.

1.3 B.3: Two exact expressions for $x = 0$

Next we evaluate the integral in Eq. 70 at $x = 0$ and note that the resulting integrand is symmetric with respect to $\eta = 0$. As a result, Eq. 70 takes the form

$$\begin{aligned} |\psi (0,t)|^{2} = \frac{2}{\pi L} \int _{0}^{1} {\rm d}\eta \, \frac{1}{\eta } \sin \left[ \frac{\eta }{2 \tau (t)} (1-\eta )\right] . \end{aligned}$$

(71)

We can obtain an alternate form by the change of variables $\chi \equiv 4 \eta (1-\eta )$ and $\chi$ covers the interval [0, 1] twice as $\eta$ moves from 0 to 1. Indeed, for $0< \eta < 1/2$ we have $\eta \equiv {\textstyle {1\over 2}}(1 - \sqrt{1 - \chi })$, while for $1/2< \eta < 1$ we have $\eta \equiv {\textstyle {1\over 2}}(1 + \sqrt{1 - \chi })$ and the corresponding differentials are $d \chi = 4 \sqrt{1 - \chi } {\rm d}\eta$ and $d \chi = -4 \sqrt{1 - \chi }\,{\rm d}\eta$, respectively.

When we decompose the integral

$$\begin{aligned} I \equiv \int _{0}^{1} {\rm d}\eta \, \frac{1}{\eta } \sin \left[ \frac{\eta }{2 \tau } (1-\eta )\right] \end{aligned}$$

(72)

into these two domains we find

$$\begin{aligned} I&= \int _{0}^{1} {\rm d}\chi \, \frac{ \sin \left[ \chi /(8 \tau ) \right] }{2\sqrt{1-\chi } \left( 1 - \sqrt{1-\chi } \right) } \nonumber \\&\quad - \int _{1}^{0} {\rm d}\chi \, \frac{ \sin \left[ \chi /(8 \tau ) \right] }{2\sqrt{1-\chi } \left( 1 + \sqrt{1-\chi } \right) } , \end{aligned}$$

(73)

or

$$\begin{aligned} I = \int _{0}^{1} {\rm d}\chi \, \frac{ \sin \left[ \chi / (8 \tau ) \right] }{\chi \sqrt{1 - \chi }} . \end{aligned}$$

(74)

Hence, we obtain the alternate exact expression

$$\begin{aligned} |\psi (0,t)|^2 = \frac{2}{\pi L} \int _{0}^{1} {\rm d}\chi \, \frac{\sin \left[ \chi /(8 \tau (t)) \right] }{\chi \sqrt{1 - \chi }} , \end{aligned}$$

(75)

for the time-dependent probability density at $x = 0$.

1.4 B.4: Approximations

Now we analyze the integrals of Eqs. 71 and 75 in three different time regimes. Our main interest is to estimate the probability density around the time of focusing.

1.4.1 B.4.1: Early times

In this domain we use the integral representation, Eq. 71, of $|\psi (0,t)|^{2}$ and note that for $t \rightarrow 0$, that is for $\tau \rightarrow 0$ two dominant terms emerge. Indeed, when we complete the square in the argument of the sine function we find

$$\begin{aligned} \eta (1 - \eta ) = \frac{1}{4} - \left( \eta - \frac{1}{2}\right) ^{2} , \end{aligned}$$

(76)

indicating a point of stationary phase at $\eta =1/2$.

Moreover, due to the factor $1/\eta$ in the integrand another contribution arises. These observations suggest to decompose the integral into two parts: one around the origin and one containing the point of stationary phase, that is

$$\begin{aligned} \int _{0}^{1} {\rm d}\eta \, f(\eta ) = \int _{0}^{a} {\rm d}\eta \, f(\eta ) + \int _{a}^{1} {\rm d}\eta \, f(\eta ) \end{aligned}$$

(77)

with

$$\begin{aligned} f(\eta ) \equiv \frac{1}{\eta }\sin \left[ \frac{1}{2\tau }\eta (1 - \eta )\right] . \end{aligned}$$

(78)

Here a is a constant parameter such that $0< a < 1/2$.

In the first integral, we approximate $\eta (1-\eta ) \cong \eta$ and take the limit $\tau \rightarrow 0$. This procedure leads us to

$$\begin{aligned} \int _{0}^{a} {\rm d}\eta \, f(\eta )&\cong \int _{0}^{a} {\rm d}\eta \, \frac{\sin \left( \eta / 2 \tau \right) }{\eta }\nonumber \\&\cong \pi \int _{0}^{a} {\rm d}\eta \, \delta (\eta ) \cong \frac{\pi }{2} , \end{aligned}$$

(79)

where we have used the representation

$$\begin{aligned} \lim _{\epsilon \rightarrow 0}\frac{\sin (x/\epsilon )}{x} = \pi \delta (x) \end{aligned}$$

(80)

of the Dirac delta function.

We evaluate the second integral in Eq. 77 with the help of the method of stationary phase [93] which yields

$$\begin{aligned} \int _{a}^{1} {\rm d}\eta \, f(\eta ) \cong 2 \sqrt{2 \pi \tau } \sin \left( \frac{1}{8 \tau } - \frac{\pi }{4} \right) . \end{aligned}$$

(81)

Finally, we combine the two results and arrive at the approximate expression

$$\begin{aligned} |\psi (0, t)|^2 \cong \frac{1}{L} \left[ 1 + 4 \sqrt{\frac{2\hbar t}{\pi M L^{2}}} \sin \left( \frac{M L^{2}}{8 \hbar t}-\frac{\pi }{4} \right) \right] , \end{aligned}$$

(82)

which reproduces the initial value of the wave packet and yields a strongly oscillatory correction with a square root envelope. Indeed, these features stand out most clearly when we express this formula in terms of the characteristic time

$$\begin{aligned} T = \frac{M L^{2}}{2\pi \hbar } \end{aligned}$$

(83)

which yields

$$\begin{aligned} |\psi (0, t)|^2 = \frac{1}{L} \left\{ 1 + \frac{4}{\pi }\sqrt{\frac{t}{T}} \sin \left[ \frac{\pi }{4}\left( \frac{T}{t} - 1 \right) \right] \right\} . \end{aligned}$$

(84)

The simplicity of this asymptotic expression for $|\psi |^{2}$ clearly motivates the inclusion of the sometimes mysterious factor $2\pi$ in the definition of T.

Equation 82 is in perfect agreement with Eq. 58, that is with our expression of Eq. 14 for $x=0$. Needless to say, for $t \rightarrow \infty$ this approximate formula, originally constructed for small times, breaks down. Indeed, we find

$$\begin{aligned} |\psi (0, t)|^2 \cong \frac{1}{L} \left[ 1 - \frac{4}{\pi }\sqrt{\frac{t}{T}} \sin \left( \frac{\pi }{4}\right) \right] \end{aligned}$$

(85)

leading to unphysical negative probabilities.

Fig. 14

Comparison between different approximations of the probability density $|\psi (x=0,t)|^{2}$. The red line represents the exact result obtained numerically from the Fresnel diffraction integral, Eq. 5, and the black curve shows the early-time estimate given by Eq. 82. In blue we depict the intermediate and long-time estimate defined by Eq. 89, and the green curve shows the 1 / t-behavior at very long times following from Eq. 93. The different curves show progressively the behavior of $|\psi (x=0,t)|^{2}$ as time increases, or equivalently, as one moves from the near-field to the far-field. Near-field: the square root envelope is visible and agrees perfectly with the exact result both in amplitude and in phase. Focusing: all approximations—except for the very long time curve in green—show a peak located close to the actual maximum. Far-field: all the approximations reproduce the asymptotics, except for the black curve at very long times

1.4.2 B.4.2: Time of maximum and long-time approximation

Next we use the representation of $|\psi (x=0, t)|^{2}$ given by Eq. 75 to obtain an estimate for long times, that is for $1 < \tau$, which captures the focusing effect as it manifests itself in a dominant maximum of the probability density. Since in this regime, the function $\sin (\chi /8 \tau )$ does not display oscillations in the interval $0<\chi <1$, we may approximate it by a line secant to the curve $\sin (\chi /8 \tau )/\chi$ at the end points, that is

$$\begin{aligned} \frac{1}{\chi }\sin \left( \frac{\chi }{8 \tau } \right) \cong \frac{1}{8 \tau } + \left[ \sin \left( \frac{1}{8 \tau } \right) -\frac{1}{8 \tau }\right] \chi . \end{aligned}$$

(86)

With this approximation and the integral relations

$$\begin{aligned} \int _{0}^{1} {\rm d}\chi \, \frac{1}{\sqrt{1 - \chi }} = 2 \end{aligned}$$

(87)

and

$$\begin{aligned} \int _{0}^{1} {\rm d}\chi \, \frac{\chi }{\sqrt{1 - \chi }} = \frac{4}{3} \end{aligned}$$

(88)

we can carry out the integration in Eq. 75 to obtain the formula

$$\begin{aligned} |\psi (0, t)|^2 \cong \frac{M L}{2 \pi \hbar t} + \frac{8}{3 \pi L} \left[ \sin \left( \frac{M L^{2}}{8 \hbar t} \right) - \frac{M L^{2}}{8 \hbar t} \right] , \end{aligned}$$

(89)

or when expressed in terms of T

$$\begin{aligned} |\psi (0, t)|^2 \cong \frac{1}{L} \left\{ \frac{T}{t} + \frac{8}{3 \pi } \left[ \sin \left( \frac{\pi }{4}\frac{T}{t} \right) - \frac{\pi }{4}\frac{T}{t} \right] \right\} , \end{aligned}$$

(90)

This expression clearly shows the asymptotic behavior T / t, as well as the presence of a maximum due to the sign change of the second term.

1.4.3 B.4.3: Very long times

A rather straight-forward approximation valid for extremely long times results from a Taylor expansion of the integral representation, Eq. 66, of the probability density in 1 / t. Indeed, for $M(x - y)/t \cong 0$, we obtain

$$\begin{aligned} |\psi (x,t)|^2 \cong \frac{M}{t} \int _{-\infty }^{\infty } {\rm d}y\, W_{0}(y, 0) , \end{aligned}$$

(91)

which together with the expression Eq. 64 of the Wigner function for $p = 0$, that is with

$$\begin{aligned} W_{0}(x, 0) = \frac{2}{\pi \hbar L} \varTheta \left( \frac{1}{2}L - |x|\right) \left( \frac{1}{2}L - |x|\right) \end{aligned}$$

(92)

yields after integration the approximate but analytical formula

$$\begin{aligned} |\psi (x,t)|^2 \cong \frac{M L}{2\pi \hbar t} = \frac{1}{L}\frac{T}{t} , \end{aligned}$$

(93)

which is independent of the coordinate x. In particular, Eq. 93 is valid for $x=0$ and it coincides with the first term of our previous estimate, Eq. 89, as shown in Fig. 14 by the blue and green curves.

1.5 B.5: Location of the focus

We are now in the position to determine the exact location of the dominant maximum of $|\psi (x=0, t)|^{2}$, that is of the focus by solving a transcendental equation. For this purpose we differentiate the exact expression for $|\psi (x=0,t)|^{2}$ in terms of the integral, Eq. 71, with respect to t which leads us to the equation

$$\begin{aligned} \int _{0}^{1} {\rm d}\eta \, (1-\eta ) \cos \left[ \frac{\eta (1-\eta )}{2 \tau } \right] = 0 , \end{aligned}$$

(94)

or

$$\begin{aligned} \cos \left( \frac{1}{8 \tau } \right) C \left( \frac{1}{2 \sqrt{\pi \tau }} \right) + \sin \left( \frac{1}{8 \tau } \right) S \left( \frac{1}{2 \sqrt{\pi \tau }} \right) = 0 . \end{aligned}$$

(95)

Here we have recalled the definitions Eqs. 8 and  9. When we solve Eq. 95 numerically we find $\tau _{f} \approx 0.054$.

A comparison between the definition, Eq. 83, of the characteristic time T with the definition, Eq. 69 of $\tau$, yields the relation

$$\begin{aligned} \tau = \frac{1}{2\pi }\frac{t}{T} , \end{aligned}$$

(96)

which translates into $t_{f}/T \equiv 2\pi \tau _{f} \cong 0.34$, in complete agreement with the analysis of Sect. 2, and in particular Figs. 1 and 2.

It is interesting that our estimates based on the various approximations for $|\psi (x=0,t)|^{2}$ discussed before are very close to this value. Indeed, our early-time approximation, Eq. 82, provides us with the condition

$$\begin{aligned} \cot \left( \frac{1}{8 \tau } -\frac{\pi }{4} \right) = 4 \tau \end{aligned}$$

(97)

leading to the value $\tau _{e} \approx 0.058$.

Remarkably, our long-time approximation, Eq. 89, which yields the transcendental equation

$$\begin{aligned} \cos \left( \frac{1}{8 \tau } \right) + \frac{1}{2} = 0 \end{aligned}$$

(98)

with the solution $\tau _{l} \equiv 3 / (16 \pi ) \approx 0.059$ is also accurate up to two digits.

Appendix C: Circular apertures

Slits are frequently employed in diffraction problems because of the mathematical simplicity of the resulting diffraction integrals and the physical interpretation being limited to one space dimension only. However, circular apertures are often preferred due to their direct application in microscopy, photography and transmission between different regions of space. Indeed, early optics problems such as the camera obscura [3], the transmission by an aperture smaller than the wave length [19, 20, 22, 31], the Fourier optics of pupils and their optical transfer functions [94] are only but a few examples illustrating this point. In this Appendix, we first briefly review the history of diffraction from a circular aperture, and then discuss the similarities and differences between the diffractive focusing of scalar waves arising from slits and circular apertures.

1.1 C.1: Cusps and multiple diffraction

We start by recalling that the Poisson–Arago spot is the intensity map resulting from the illumination of a circular disk. Therefore, the field distribution is the complement of that generated by a circular aperture and can be calculated using the Babinet principle [95–98].

In 1922, Coulson and Becknell⁷ have investigated experimentally a variant of the Poisson–Arago spot [101, 102] by measuring the intensity patterns generated by a disk rotated around its diagonal and illuminated by a point light source. The geometric shadow of this arrangement is an ellipse and the intensity pattern in the far-field is a diamond-like figure with four cusps being the evolute of the edge of the shadow. It is interesting that a few years earlier, Raman has also observed cusps in the diffraction patterns generated by an elliptical aperture [103].

Cusp are examples of catastrophe optics [99]. The interaction of light with a sharp-edge aperture was mathematically reformulated recently [104].

Finally, we turn to Letfullin and collaborators who have analyzed [105–109] theoretically and experimentally the phenomenon of multiple diffractive focusing, which occurs when we apply a second circular aperture of radius $a_{2}$ to the diffraction pattern generated by a first circular aperture of larger diameter $a_{1}$, placed in the symmetry axis. Provided the distance L between the second and the first apertures is such that the Fresnel number $N_{1} \equiv a_{1}^{2}/(\lambda L)$ is an odd integer, the second diffraction pattern has a maximum that can reach 10.0 times the illuminating intensity of the first aperture. Based on this observation they proposed a lens for matter waves [110].

1.2 Slit and circular aperture: paraxial versus non-paraxial optics

In Sect. 4 we have studied the diffraction from a slit of width L illuminated by light of wave length $\lambda$ using the Fresnel and the Rayleigh–Sommerfeld integrals. The evaluation of the RS-I integral requires the numerical integration of Hankel functions [77]. We now briefly summarize an analogous discussion for the case of a circular aperture of radius $a = L/2$.

In the Fresnel diffraction from a circular aperture we make use of Lommel functions in the calculation algorithm [77, 84–86]. For the non-paraxial calculation, the RS-I and RS-II integrals are evaluated numerically using the GNU Scientific Library (GSL) [111]. The results for the slit and the circular aperture are depicted in Figs. 11 and 12 in Sect. 6.

The fields and the corresponding normalized intensities on-axis based on the Rayleigh–Sommerfeld integrals for a circular aperture of radius a illuminated by a plane wave [43, 45, 77] read

$$\begin{aligned} \left\{ \begin{array}{lll} U_{\text {RS-I}}(z) &{}= U_{0}\left( {\rm e}^{ikz} - \frac{\displaystyle z}{\displaystyle \sqrt{a^{2} + z^{2}}} {\rm e}^{ik\sqrt{a^{2} + z^{2}}}\right) \\ U_{\text {RS-II}}(z) &{}= U_{0}\left( {\rm e}^{ikz} - {\rm e}^{ik\sqrt{a^{2} + z^{2}}}\right) \\ \end{array} \right. \end{aligned}$$

(99)

and

$$\begin{aligned} \left\{ \begin{array}{lll} \frac{I_{\text {RS-I}}}{I_{0}} &{}= 1 + \frac{\displaystyle z^{2}}{\displaystyle z^{2} + a^{2}} \\ &{}\quad - 2\frac{\displaystyle z}{\displaystyle \sqrt{z^{2} + a^{2}}}\cos \left[ k\left( \sqrt{a^{2} + z^{2}} - z\right) \right] \\ \frac{I_{\text {RS-II}}}{I_{0}} &{}= 2 - 2\cos \left[ k\left( \sqrt{a^{2} + z^{2}} - z\right) \right] .\\ \end{array} \right. \end{aligned}$$

(100)

From these expressions,⁸ especially the one for $I_{RS-II}/I_{0}$, several properties of the non-paraxial diffraction stand out: the number of maxima, or minima of each intensity function is finite. Indeed, the maxima follow from the condition

$$\begin{aligned} \cos \left[ k(\sqrt{a^{2} + z^{2}} - z) \right] = -1 , \end{aligned}$$

(101)

or equivalently, $k(\sqrt{a^{2} + z^{2}} - z) = (2m + 1)\pi$, with $m = 0, 1, 2, \dots$ The minima occur when

$$\begin{aligned} k(\sqrt{a^{2} + z^{2}} - z) = 2 n\pi , \end{aligned}$$

(102)

with $n = 1, 2, \dots$

The argument of the cosine function never vanishes, except for the trivial case of $a = 0$, or in the asymptotic limit $z \rightarrow \infty$. On the other hand, the intensity at the origin ($z = 0$) oscillates between 0 and 4.0, depending only on a. In contrast, the intensity $I_{\text {RS-I}}/I_{0}$ always converges to 1.0.

The representation of the on-axis intensities $I_{\text {RS-I}}$ and $I_{\text {RS-II}}$ using a logarithmic scale for z permits us to find another interesting property of the non-paraxial diffraction: the separation between maxima, or minima along the $\log (z)$-axis is constant. This property is due to the argument of cosine function.

We note that Forbes has investigated the scaling properties of the Fresnel diffraction patterns for circular apertures [92], but he did not mention this feature as it arises only in non-paraxial diffraction.

The Fresnel diffraction intensity on-axis of a circular aperture reads

$$\begin{aligned} I_{\rm Fc}(0, 0, z) = 2 - 2\cos \left( \frac{k a^{2}}{2 z}\right) , \end{aligned}$$

(103)

with the argument of the cosine-function being inversely proportional to z. Thus, the number of maxima and minima is infinite.

We can find the location $z_{\rm m} = a/\lambda$ of the last maximum from Eq. 103. If we normalize this length by $L^{2} / \lambda$ we obtain

$$\begin{aligned} z^{(2)}_{f} / (L^{2}/\lambda ) = 0.25 , \end{aligned}$$

(104)

that is the position of the focus.

In the case of the slit no analytic expressions are known for the non-paraxial intensity, but the graphical representations of the RS-I intensities in Fig. 11 show that the number of lobes in the intensity map of a slit of width $L=2a$ is equal to that for a circular aperture of the same diameter. It depends only on the ratio $L/\lambda$.

However, the maxima are differently distributed along the z-axis, and the dominant lobe containing the focusing maximum is much more elongated than that of the circular aperture.

The Fresnel intensity on-axis is approximated by

$$\begin{aligned} I_{\rm Fs}(0, 0, z) \approx 1 - \frac{2 \sqrt{z}}{\pi L}\cos \left( \frac{\pi }{4} + \frac{k L^{2}}{8 z}\right) , \end{aligned}$$

(105)

which shows why the position of the focus is shifted towards larger z values, compared to the circular aperture. After the normalization by $L^{2}/\lambda$ we find

$$\begin{aligned} z^{(1)}_{f}/(L^{2}/\lambda ) = 0.33 \end{aligned}$$

(106)

Moreover, the maxima of the Fresnel intensity decay in amplitude converging to 1.0 for $z \rightarrow 0$, unlike in the circular aperture.