A novel technique to achieve atomic macro-coherence as a tool to determine the nature of neutrinos

Abstract

The photon spectrum in macro-coherent atomic deexcitation via radiative emission of neutrino pairs has been proposed as a sensitive probe of the neutrino mass spectrum, capable of competing with conventional neutrino experiments. In this paper, we revisit this intriguing possibility, presenting an alternative method for inducing large coherence in a target based on adiabatic techniques. More concretely, we propose the use of a modified version of coherent population return (CPR), namely two-photon CPR, that turns out to be extremely robust with respect to the experimental parameters and capable of inducing a coherence close to 100 % in the target.

Appendices

Appendix 1: Mathematical analysis of CPR

Let us consider a two-state system with bare states $\{|\psi _1\rangle ,|\psi _2\rangle \}$ interacting with a laser field whose frequency $\omega _{{L}}$ is detuned from the Bohr frequency by $\Delta = E_{21}-\omega _{{L}}$, where ${E_{21}}={E_{2}}-{E_{1}}$. In the diabatic basis B formed by the states $\{|\psi _1\rangle ,|\psi _2\rangle \}$, we can define the statevector of the system $|\Psi (t)\rangle$ as

$$|\Psi (t)\rangle =c_1(t)|\psi _1\rangle +c_2(t)|\psi _2\rangle ,$$

(34)

and consequently the Schrödinger equation can be written as:

$$\left( \begin{array}{c} \dot{c}_1(t) \\ \dot{c}_2(t)\end{array}\right) =-\frac{{i}}{2}\left( \begin{array}{cc} 0 &{} \Omega (t)\\ \Omega (t) &{} 2\Delta \end{array} \right) \left( \begin{array}{c}c_1(t) \\ c_2(t)\end{array}\right) .$$

(35)

The adiabatic basis B’ $\{|\Phi _-(t)\rangle , |\Phi _+(t)\rangle \}$ that diagonalizes the Hamiltonian of Eq. 6 can be written as

$$\begin{aligned} |\Phi _- (t)\rangle&=\cos \vartheta (t)|\psi _1\rangle - \sin \vartheta (t)|\psi _2\rangle \\ |\Phi _+ (t)\rangle&=\sin \vartheta (t)|\psi _1\rangle +\cos \vartheta (t)|\psi _2\rangle , \end{aligned}$$

(36)

with associated eigenvalues $\left( \lambda _+(t), \lambda _-(t)\right)$

$$\lambda _\mp (t)=\frac{1}{2}\left[ \Delta \mp \sqrt{\Omega ^2(t) +\Delta ^2}\right]$$

(37)

where the mixing angle is defined by

$$\vartheta (t)=(1/2)\arctan [\Omega (t)/\Delta ].$$

(38)

Accordingly, the eigenvector of the system in both bases can be the written as

$$|\Psi (t)\rangle =c_1(t)|\psi _1\rangle +c_2(t)|\psi _2\rangle = c_-(t)|\Phi _- (t)\rangle +c_+(t)|\Phi _+ (t)\rangle ,$$

(39)

being the matrix that defines the basis change B’$\rightarrow$B defined by

$$R\left[ \vartheta (t)\right] = \left( \begin{array} {cc} \cos \vartheta &{} \sin \vartheta \\ -\sin \vartheta &{} \cos \vartheta \end{array} \right) .$$

(40)

Taking into account that

$$|\Psi (t)\rangle _{{B}}=R\left[ \vartheta (t)\right] |\Psi (t)\rangle _{{B'}}$$

(41)

and

$$H_{{B}}(t)=R\left[ \vartheta (t)\right] H_{{B}'}(t)R^{{T}}\left[ \vartheta (t)\right]$$

(42)

it is possible to express the Schrödinger equation of Eq. 5 in the basis B’:

$$i\hbar \frac{\partial {|\Psi (t)\rangle _{{B}'}}}{\partial t}= \left( H_{{B}'}(t)-i\hbar R^{{T}}\left[ \vartheta (t)\right] \dot{R}\left[ \vartheta (t)\right] \right) |\Psi (t)\rangle _{{B}'}.$$

(43)

According to the previous definition, we can write Eq. 43 as

$$\left( \begin{array}{c} \dot{c}_-(t) \\ \dot{c}_+(t)\end{array}\right) =-{i}\left( \begin{array}{cc} \lambda _- &{} -i\dot{\vartheta }(t)\\ i\dot{\vartheta }(t) &{} \lambda _+ \end{array} \right) \left( \begin{array}{c} c_-(t) \\ c_+(t)\end{array}\right) .$$

(44)

According to Eq. 44 and in a situation where the non-diagonal terms are negligible with respect to the diagonal ones, if the statevector $|\Psi (t)\rangle$ of the system is initially aligned with one of the adiabatic eigenstates, i.e., $|\Phi _+(t)\rangle$ or $|\Phi _-(t)\rangle$, it will remain parallel to it during the whole excitation process, i.e., the system will evolve adiabatically. Mathematically, the adiabatic condition can be expressed as

$$\lambda _+(t)-\lambda _-(t)\gg |\dot{\vartheta }(t)|,$$

(45)

which turns out into the simple expression [25]:

$$|\Delta |\ge \frac{1}{\tau }$$

(46)

being $\tau$ the laser pulse duration. It is important to notice that the adiabatic region is exclusively determined by the laser detuning with respect to resonance and the duration of the laser pulse (or equivalently the laser bandwidth), being thus independent from the Rabi frequency $\Omega (t)$. This makes CPR an extremely robust technique for its experimental implementation because these parameters are easily controllable in a real experiment.

Appendix 2: Adiabatic basis projection

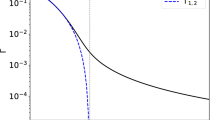
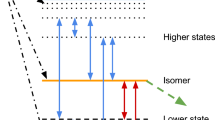
Figures 9, 10 and 11 show the square of the components of the vectors $|\Phi _{{i}}\rangle$, i.e., the projection $|\langle \psi _{{j}}|\Phi _{{i}}\rangle |^2$ for $i,j=1,2,3$ as a function of time for a situation where $\Omega _{{P}}=\Omega _{{S}}=\Omega _{0{p}}\exp {(-t^2/\tau ^2)}$ with $\tau =6$  a.u., $\Delta _{{ S}}=(14/9)\Delta _{{P}}$, and $\Omega _{0{p}}/\Delta _{{ P}}=50/9$. At the beginning of the interaction, the adiabatic vector aligned with $|\psi _1\rangle$ (assuming all the population starts in the ground state) is $|\Phi _2\rangle$, being therefore the statevector of the system parallel to both. The statevector of the system will remain parallel to $|\Phi _2\rangle$ if the evolution is adiabatic.

Fig. 9

(Color online) $|\Phi _1\rangle$ projection

Fig. 10

(Color online) $|\Phi _2\rangle$ projection

Fig. 11

(Color online) $|\Phi _3\rangle$ projection

Appendix 3: Angle of rotation and axis

Defining the rotation axis ${\mathbf {u}} =(u_{{x}}, u_{{y}}, u_{{z}})$ and with the help of the eigenvalues Z$_i$ (see Eq. 13) and the normalization parameters $\xi _i$ (see Eq. 17), the different components can be written as:

$$\begin{aligned} u_{{x}}&= -\frac{a_1}{b_1 \sqrt{\frac{c_1+d_1+e_1+f_1}{g_1}}}\nonumber \\ a_1&= 2 Z_1 \xi _1(Z_1-\Delta _{{P}}+\Delta _{{S}}+Z_3 (-Z_1+Z_3) \xi _3 \Omega _{{S}})\nonumber \\ b_1&= -1+Z_3 \xi _3 \Omega _{{S}}+\xi _1 \Omega _{{P}} (Z_1-\Delta _{{P}}+\Delta _{{S}}-(Z_1-Z_3) (\Delta _{{S}}-\Delta _{{S}}) \xi _3 \Omega _{{S}})\nonumber \\ c_1&= 1+4 Z_1^2 (Z_1-\Delta _{{P}}+\Delta _{{S}})^2 \xi _1^2+4Z_3^4 \xi _3^2-4 Z_3^2 (\Delta _{{P}}-\Delta _{{S}}) (2 Z_3-\Delta _{{P}}+\Delta _{{S}}) \xi _3^2\nonumber \\ d_1& = Z_3 \xi _3 \Omega _{{S}} \left( -2-8Z_1^2 (Z_1-Z_3) (Z_1-\Delta _{{P}}+\Delta _{{S}}) \xi _1^2+Z_3 \left( 1+4 Z_1^2 (Z_1-Z_3)^2\xi _1^2\right) \xi _3 \Omega _{{S}}\right) \nonumber \\ e_1&= \xi _1^2 \Omega _{{P}}^2 ((Z_1-\Delta _{{P}}+\Delta _{{S}})^2 (1+4 (Z_1-Z_3)^2 (Z_3-\Delta _{{P}}+\Delta _{{S}})^2 \xi _3^2)\nonumber \\&\quad+ (Z_1-Z_3) (\Delta _{{P}}-\Delta _{{S}}) \xi _3 \Omega _{{S}} (-2 (Z_1-\Delta _{{P}}+\Delta _{{S}})+(Z_1-Z_3) (\Delta _{{P}}-\Delta _{{S}}) \xi _3 \Omega _{{S}}))\nonumber \\ f_1&= 2 \xi _1 \Omega _{{P}} ((Z_1-\Delta _{{P}}+\Delta _{{S}}) (-1+4 (Z_1-Z_3) Z_3 (Z_3-\Delta _{{P}}+\Delta _{{S}})^2 \xi _3^2 )\nonumber \\&\quad+\xi _3 \Omega _{{S}} (Z_1 (Z_3+\Delta _{{P}}-\Delta _{{S}})+ + 2 Z_3 (-\Delta _{{P}}+\Delta _{{S}})+Z_3 (-Z_1+Z_3) (\Delta _{{P}}-\Delta _{{S}}) \xi _3 \Omega _{{S}}))\nonumber \\ g_1&= (1-Z_3\xi _3 \Omega _{{S}}+\xi _1 \Omega _{{P}} (-Z_1+\Delta _{{P}}-\Delta _{{S}}+(Z_1-Z_3) (\Delta _{{P}}-\Delta _{{S}}) \xi _3 \Omega _{{S}}))^2 \end{aligned}$$

(47)

$$\begin{aligned} u_{{y}}&= \frac{(a_2+b_2)}{\sqrt{c_2-d_2-e_2+f_2}}\nonumber \\ a_2&= 1-Z_3 \xi _3 \Omega _{{S}}\nonumber \\ b_2&= \xi _1 \Omega _{{P}} (-Z_1+\Delta _{{P}}-\Delta _{{S}}+(Z_1-Z_3) (\Delta _{{P}}-\Delta _{{S}}) \xi _3\Omega _{{S}})\nonumber \\ c_2&= 1+4 Z_1^2 (Z_1-\Delta _{{P}}+\Delta _{{S}})^2 \xi _1^2+4 Z_3^4 \xi _3^2-4 Z_3^2(\Delta _{{P}}-\Delta _{{S}}) (2 Z_3-\Delta _{{P}}+\Delta _{{S}}) \xi _3^2\nonumber \\ d_2&= Z_3 \xi _3 \Omega _{{S}} (-2-8 Z_1^2 (Z_1-Z_3) (Z_1-\Delta _{{P}}+\Delta _{{S}}) \xi _1^2+Z_3(1+4 Z_1^2 (Z_1-Z_3)^2\xi _1^2) \xi _3 \Omega _{{S}})\nonumber \\ e_2&= \ \xi _1^2 \Omega _{{P}}^2 ((Z_1-\Delta _{{P}}+\Delta _{{S}})^2 (1+4 (Z_1-Z_3)^2 (Z_3-\Delta _{{P}}+\Delta _{{S}})^2 \xi _3^2)+\nonumber \\&\quad+ (Z_1-Z_3) (\Delta _{{P}}-\Delta _{{S}}) \xi _3 \Omega _{{S}} (-2 (Z_1-\Delta _{{P}}+\Delta _{{S}})+(Z_1-Z_3) (\Delta _{{P}}-\Delta _{{S}}) \xi _3 \Omega _{{S}}))\nonumber \\ f_2= & {} 2 \xi _1\Omega _{{P}} ((Z_1-\Delta _{{P}}+\Delta _{{S}}) (-1+4 (Z_1-Z_3) Z_3 (Z_3-\Delta _{{P}}+\Delta _{{S}})^2 \xi _3^2)\nonumber \\&\quad+\xi _3 \Omega _{{S}} (Z_1 (Z_3+\Delta _{{P}}-\Delta _{{S}})+ +2 Z_3 (-\Delta _{{P}}+\Delta _{{S}})+Z_3 (-Z_1+Z_3)(\Delta _{{P}}-\Delta _{{S}}) \xi _3 \Omega _{{S}})) \end{aligned}$$

(48)

$$\begin{aligned} u_{{z}}&= \frac{a_3}{b_3 \sqrt{\frac{c_3+d_3+e_3+f_3}{g_3}}}\nonumber \\ a_3&= 2 (Z_3-\Delta _{{P}}+\Delta _{{S}}) \xi _3 (Z_3+(Z_1-Z_3) (Z_1-\Delta _{{P}}+\Delta _{{S}}) \xi _1 \Omega _{{P}}) \nonumber \\ b_3&= 1-Z_3 \xi _3 \Omega _{{S}}+\xi _1 \Omega _{{P}} (-Z_1+\Delta _{{P}}-\Delta _{{S}}+(Z_1-Z_3)(\Delta _{{P}}-\Delta _{{S}}) \xi _3 \Omega _{{S}}) \nonumber \\ c_3&= 1+4 Z_1^2 (Z_1-\Delta _{{P}}+\Delta _{{S}})^2 \xi _1^2+4 Z_3^4 \xi _3^2-4 Z_3^2 (\Delta _{{P}}-\Delta _{{S}}) (2 Z_3-\Delta _{{P}}+\Delta _{{S}}) \xi _3^2 \nonumber \\ d_3&= Z_3 \xi _3 \Omega _{{S}} (-2-8 Z_1^2 (Z_1-Z_3) (Z_1-\Delta _{{P}}+\Delta _{{S}})\xi _1^2+Z_3 (1+4 Z_1^2 (Z_1-Z_3)^2 \xi _1^2) \xi _3 \Omega _{{S}}) \nonumber \\ e_3&= \xi _1^2 \Omega _{{P}}^2 ((Z_1-\Delta _{{P}}+\Delta _{{S}})^2 (1+4 (Z_1-Z_3)^2 (Z_3-\Delta _{{P}}+\Delta _{{S}})^2 \xi _3^2)+\nonumber \\&\quad+ (Z_1-Z_3) (\Delta _{{P}}-\Delta _{{S}}) \xi _3 \Omega _{{S}} (-2 (Z_1-\Delta _{{P}}+\Delta _{{S}})+(Z_1-Z_3) (\Delta _{{P}}-\Delta _{{S}}) \xi _3 \Omega _{{S}})) \nonumber \\ f_3&= 2 \xi _1 \Omega _{{P}} ((Z_1-\Delta _{{P}}+\Delta _{{S}}) (-1+4 (Z_1-Z_3) Z_3 (Z_3-\Delta _{{P}}+\Delta _{{S}})^2 \xi _3^2)\nonumber \\&\quad+\xi _3 \Omega _{{S}} (Z_1 (Z_3+\Delta _{{P}}-\Delta _{{S}}) + 2 Z_3 (-\Delta _{{P}}+\Delta _{{S}})+Z_3 (-Z_1+Z_3) (\Delta _{{P}}-\Delta _{{S}}) \xi _3 \Omega _{{S}})) \nonumber \\ g_3&= (1-Z_3\xi _3 \Omega _{{S}}+\xi _1 \Omega _{{P}} (-Z_1+\Delta _{{P}}-\Delta _{{S}}+(Z_1-Z_3) (\Delta _{{P}}-\Delta _{{S}}) \xi _3 \Omega _{{S}}))^2 \end{aligned}$$

(49)

Figure 12 shows the components $u_{{x}}, u_{{y}}$ and $u_{{z}}$ as a function of time.

Fig. 12

(Color online) Components $u_{{x}}, u_{{y}}$ and $u_{{z}}$ of the rotation axis as a function of time for a situation where $\Omega _{{P}}=\Omega _{{S}}=\Omega _{0{p}}\exp {(-t^2/\tau ^2)}$ with $\tau =6$  a.u., $\Delta _{{S}}=2\Delta _{{P}}$, and $\Omega _{0{p}}/\Delta _{{P}}=4$

The rotation angle $\alpha$ (see Eq. 23) can be written as:

$$\alpha =\arccos \frac{u_{{x}}^2-Z_1 \xi _1\Omega _{{P}}+(\Delta _{{P}}-\Delta _{{S}}) \xi _1 \Omega _{{P}}}{u_{{x}}^2-1}$$

(50)

Figure 13 shows the angle of rotation $\alpha$ as a function of time.

Fig. 13

(Color online) Angle of rotation $\alpha$ as a function of time for the same parameters that Fig. 12

Appendix 4: Adiabatic conditions

The evolution of the system will be diabatic if the following conditions, assuming $\Omega _{{P,S}}\rightarrow 0$, are fullfilled

$$\begin{aligned} \left| Z_1-Z_2 \right| =\left| p\left( \cos \frac{\theta }{3}-\frac{\sqrt{3}}{3}\sin \frac{\theta }{3}\right) \right|&= 0\\ \left| Z_3-Z_2 \right| =\left| \frac{2\sqrt{3}}{3}p\sin \frac{\theta }{3}\right|&= 0. \end{aligned}$$

(51)

A possible solution of these equations is $p=0$, being p defined by Eqs. 12 and 14. Since $\Omega _{{P,S}}\rightarrow 0$, the different parameters can be written as

$$\begin{aligned} a&=-\left( 2\Delta _{{P}}-\Delta _{{S}}\right) \\ b&=\Delta _{{P}}\left( \Delta _{{P}}-\Delta _{{S}}\right) \\ c&=0 \end{aligned}$$

(52)

and

$$p=\sqrt{a^2-3b}=\sqrt{\Delta _{{P}}^2+\Delta _{{S}}^2-\Delta _{{P}}\Delta _{{S}}}=0$$

(53)

whose solution is $\Delta _{{P}}=\Delta _{{S}}=0$. The rest of solutions are:

• 1. $\left| \cos \frac{\theta }{3}-\frac{\sqrt{3}}{3}\sin \frac{\theta }{3}\right| =0$

  $$\begin{aligned} \tan \frac{\theta }{3}&=\sqrt{3}\\ \theta&= \pi +3n\pi \\ \end{aligned}$$

  Using the expression for the angle $\theta$ (see Eq. 15), we obtain for $n=0$:

  $$\begin{aligned} &\cos \theta =\cos \,\pi =-1\\ &-\frac{-27c+2a^3-9ab}{2p^3}=-1\\ &-2\Delta _{P}^3+3\Delta _{P}^2\Delta _{S}+3\Delta _{P} \Delta _{S}^2-2\Delta _{S}^3\\ &\quad +2\left( \Delta _{P}^2-\Delta _{P}\Delta _{S}+\Delta _{S}^2\right)^{3/2}=0. \end{aligned}$$

  (54)

  This last equation has two different solutions, namely

  $$\begin{aligned} \Delta _{{P}}&=0\\ \Delta _{{P}}&=\Delta _{{S}}. \end{aligned}$$

  (55)

• 2. $\left| \frac{2\sqrt{3}}{3}\sin \frac{\theta }{3}\right| =0$

  Operating in the same way we obtain

  $$\begin{aligned} \sin \frac{\theta }{3}&=0\\ \theta&=0+3n\pi .\\ \end{aligned}$$

  Therefore, for $n=0$, we obtain

  $$\begin{aligned} &\cos \theta =\cos \,0=1\\ &-\frac{-27c+2a^3-9ab}{2p^3}=1\\ &-2\Delta _{P}^3+3\Delta _{P}^2\Delta _{S}+3\Delta _{P} \Delta _{S}^2-2\Delta _{S}^3\\ &\quad -2\left( \Delta _{P}^2 -\Delta _{P}\Delta _{S}+\Delta _{S}^2 \right)^{3/2}=0. \end{aligned}$$

  (56)

  This last equation with a correct election of the signs of the square root has the following solutions:

  $$\begin{aligned} \Delta _{{P}}&=0\\ \Delta _{{P}}&=\Delta _{{S}}. \end{aligned}$$

  (57)