Energy Bounds for a Compressed Elastic Film on a Substrate

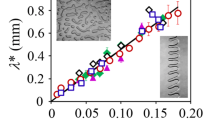
Abstract

We study pattern formation in a compressed elastic film which delaminates from a substrate. Our key tool is the determination of rigorous upper and lower bounds on the minimum value of a suitable energy functional. The energy consists of two parts, describing the two main physical effects. The first part represents the elastic energy of the film, which is approximated using the von Kármán plate theory. The second part represents the fracture or delamination energy, which is approximated using the Griffith model of fracture. A simpler model containing the first term alone was previously studied with similar methods by several authors, assuming that the delaminated region is fixed. We include the fracture term, transforming the elastic minimisation into a free boundary problem, and opening the way for patterns which result from the interplay of elasticity and delamination. After rescaling, the energy depends on only two parameters: the rescaled film thickness, ${\sigma }$, and a measure of the bonding strength between the film and substrate, ${\gamma }$. We prove upper bounds on the minimum energy of the form ${\sigma }^a {\gamma }^b$ and find that there are four different parameter regimes corresponding to different values of a and b and to different folding patterns of the film. In some cases, the upper bounds are attained by self-similar folding patterns as observed in experiments. Moreover, for two of the four parameter regimes we prove matching, optimal lower bounds.

Appendices

Appendix 1: Derivation of the Model and Rescaling

In this appendix, we derive the energy (1.1). We model the two-layer material (an elastic film on a substrate) described in the introduction with an energy consisting of two parts, an elastic energy for the thin film and a bonding energy for the interaction between the film and the substrate. We take the elastic energy to be the von Kármán energy, which penalises extension (stretching and compression) and bending:

$$\begin{aligned} \begin{aligned} {\hat{I}}_{\mathrm {vK}}&:= \frac{Eh_\mathrm {f}}{2(1-\nu ^2)} \int _{\Omega } \left\{ (1-\nu ) \left| \frac{D {\varvec{u}}+ {D {\varvec{u}}^{\text {T}}}}{2} + \frac{D w \otimes D w}{2} - \varepsilon _* \mathrm {Id}\right| ^2 \right. \\&\left. \quad + \nu \left| \mathrm {tr} \left( \frac{D {\varvec{u}}+ {D {\varvec{u}}^{\text {T}}}}{2} + \frac{D w \otimes D w}{2} - \varepsilon _* \mathrm {Id}\right) \right| ^2 \right\} \, d{\varvec{x}}\\&\phantom {==} + \frac{E h_\mathrm {f}^3}{24(1-\nu ^2)} \int _{\Omega } \left\{ (1-\nu ) | D^2 w |^2 + \nu (\Delta w)^2 \right\} \, d{\varvec{x}}\end{aligned} \end{aligned}$$

(6.43)

where $\Omega = (0,l_1) \times (0,l_2)$ is the set of material points (x, y) of the film, $h_\text {f}$ is the thickness of the film, E is the Young’s Modulus, and $\nu$ is the Poisson ratio. The functions ${\varvec{u}}(x,y) = (u(x,y),v(x,y))$ and w(x, y) are the in-plane and transversal (vertical) displacements of the film from the isotropically compressed state $((1-\varepsilon _*)x,(1-\varepsilon _*)y,0)$, where $0<\varepsilon _*<1$ is the compression ratio. Note that ${\varepsilon }_*=0$ corresponds to no compression and ${\varepsilon }_*=1$ corresponds to total compression. Thus, $(u,v,w)=(0,0,0)$ corresponds to the isotropically compressed state of the film and $(u,v,w)=(\varepsilon _* x,\varepsilon _* y,0)$ corresponds to the relaxed, natural state. The substrate is taken to be at height $z=0$. Therefore, the transversal displacement w must satisfy the constraint $w \ge 0$ (since the film cannot go below the substrate). If $w(x,y)=0$, then the material point (x, y) of the film is bonded down to the substrate.

For the energy scaling analysis that we perform, we can set the Poisson ratio $\nu$ equal to zero without loss of generality since the terms of (6.43) with value of $\nu$ in the physical range $(-1,1/2)$ can be bound from above and below by those without, as shown in Ben Belgacem et al. (2000, Appendix B).

The interfacial force between the thin film and the substrate is an attractive van der Waals force. We model it in a simple way with a bonding energy ${\hat{I}}_{\text {Bo}}$ that penalises debonding from the substrate:

$$\begin{aligned} {\hat{I}}_{\text {Bo}} := {\gamma }^* | \{ (x,y)\in \Omega \, : \, w(x,y)>0 \} | \end{aligned}$$

(6.44)

where ${\gamma }^*$ is a constant depending on the material properties of the film and the substrate. In more sophisticated models, $I_{\text {Bo}}$ would also depend on the size of w, i.e. how far the film is from the substrate.

Thus, the total energy we assign to the system is

$$\begin{aligned} {\hat{I}} := {\hat{I}}_{\text {vK}} + {\hat{I}}_{\text {Bo}}. \end{aligned}$$

(6.45)

On the boundary $\{x=0\}$, we assume that the film is fixed to the substrate and satisfies the clamped boundary conditions

$$\begin{aligned} u(0,y)=0, \quad v(0,y)=0, \quad w(0,y) = 0, \quad D w (0,y) = \mathbf{0}. \end{aligned}$$

(6.46)

(Note that in the experiments of Mei et al. (2007), the film is actually fixed to a buffer layer and satisfies slightly different boundary conditions. This is discussed in Appendix 2) The film is free on the rest of its boundary, $\{x=l_1\} \cup \{y=0\} \cup \{y=l_2\}$.

Rescaling In order to reduce the number of parameters, we define rescaled variables, denoted with a superscript $*$, by

$$\begin{aligned} {\varvec{u}}=: 2 \varepsilon _* {\varvec{u}}^*, \qquad w =: (2 \varepsilon _*)^{1/2} \, w^*. \end{aligned}$$

(6.47)

By substituting from Eq. (6.47) into Eq. (6.45), multiplying by $2 (1-\nu ^2) / (E h_\mathrm {f} \varepsilon _*^2)$, setting $\nu =0$, and dropping all the superscripts * for convenience, we obtain a new energy $I^{({\sigma },{{\gamma }})}$:

$$\begin{aligned} \begin{aligned} I^{({\sigma },{{\gamma }})}[{\varvec{u}},w,l_1,l_2]&= \int _{x=0}^{l_1} \! \int _{y=0}^{l_2} |D {\varvec{u}}+ {D {\varvec{u}}^\mathrm {T}} + D w \otimes D w - \mathrm {Id}|^2 \, {\text {d}}x \, {\text {d}}y \\&\phantom {=} + ({\sigma } l_1)^2 \int _{x=0}^{l_1} \! \int _{y=0}^{l_2} | D^2 w|^2 \, {\text {d}}x \, {\text {d}}y \\&\quad + {{\gamma }}| \{ (x,y)\in \Omega \, : \, w(x,y)>0 \} | \end{aligned} \end{aligned}$$

(6.48)

where ${\sigma }$ is the rescaled film thickness and ${{\gamma }}$ is the rescaled bonding energy per unit area:

$$\begin{aligned} {\sigma } := \frac{h_\mathrm {f}}{l_1 (6 \varepsilon _*)^{1/2}}, \qquad {{\gamma }}:=\frac{2 (1-\nu ^2) {{\gamma }}^*}{E h_\mathrm {f} \varepsilon _*^2} = \frac{2 {{\gamma }}^*}{E h_\mathrm {f} \varepsilon _*^2} \quad (\text {since } \nu =0). \end{aligned}$$

(6.49)

Throughout this paper, we refer to ${{\gamma }}$ as the bonding strength, although note that it also depends on the unscaled film thickness $h_{\text {f}}$. Equation (6.48) is exactly Eq. (1.1) given in the Introduction.

Appendix 2: Upper Bounds for Buffer Layers with Nonzero Thickness

In the experiments of Mei et al. (2007), the film is not clamped to the substrate, but rather to a thin buffer layer, and satisfies clamped boundary conditions of the form

$$\begin{aligned} u(0,y)=0, \quad v(0,y)=0, \quad w(0,y) = h_\mathrm {b}, \quad D w (0,y) = {\mathbf {0}} \end{aligned}$$

(6.50)

where $h_\mathrm {b}>0$ is the thickness of the buffer layer. In this paper, we considered the unphysical case $h_\mathrm {b}=0$ in order to simplify the analysis. In this appendix, we show that the upper bounds of Theorem 2.1 also hold when $h_\mathrm {b}$ is sufficiently small. Recall that $\Omega = (0,l_1)\times (0,l_2)$. Define

$$\begin{aligned} V_{h_{\text {b}}} \!=\! \left\{ ({\varvec{u}},w) \!\in \!H^1(\Omega ;{\mathbb {R}}^2) \!\times \! H^2(\Omega ) : w\!= \!h_{\text {b}}, \, {\varvec{u}}\!=\! D w ={\mathbf {0}}, \, \text { on } \{ 0 \} \!\times \!(0,l_2), \; w \!\ge \!0 \right\} . \end{aligned}$$

Theorem 6.8

(Upper Bounds for $h_{\text {b}} >0$) Let $0<l_1\le l_2, {\sigma }\in (0,1), {{\gamma }}\ge 0$. Assume that $h_{\text {b}}$ satisfies

$$\begin{aligned} 0 \le \frac{h_{\text {b}}}{l_1} \le \min \{ {\sigma },{\sigma }^{-1} {{\gamma }}^{-3/2} \}. \end{aligned}$$

Then, there exists admissible displacement fields $({\varvec{u}},w) \in V_{h_{\text {b}}}$ satisfying the same upper bounds as in Theorem 2.1.

Proof

We construct displacement fields satisfying the required upper bounds by simply appending to the constructions used to prove Theorem 2.1 a boundary layer in which the film is bent upwards from height 0 to height $h_{\text {b}}$. Let $\eta >0$ be the boundary layer thickness. For $x \in [0,\eta ], y \in [0,l_2]$ define

$$\begin{aligned} u = \frac{1}{2} x, \quad v = 0, \quad w = h_{\text {b}} \left[ 1 - \psi \left( \frac{x}{\eta } \right) \right] \end{aligned}$$

(6.51)

where $\psi \in C^2({\mathbb {R}})$ is a function with $\psi (t)=0$ for $t\le 0, \psi (t)=1$ for $t\ge 1$. For $x \ge \eta$, define u, v, w as in the proof of Theorem 2.1 (except that u is replaced with $u + \eta /2$). The energy $E_{\text {BL}}^\eta$ of (u, v, w) in the boundary layer $(0,\eta )\times (0,l_2)$ satisfies

$$\begin{aligned} E_{\text {BL}}^\eta \le l_2 \eta \left( \frac{h_{\text {b}}^4}{\eta ^4} + ({\sigma } l_1)^2 \frac{h_{\text {b}}^2}{\eta ^4} + 1 + {\gamma } \right) \le l_2 \eta \left( 2({\sigma } l_1)^2 \frac{h_{\text {b}}^2}{\eta ^4} + 1 + {\gamma } \right) \end{aligned}$$

(6.52)

since we assumed that $h_{\text {b}} \le {\sigma } l_1$. We choose

$$\begin{aligned} \eta = ({\sigma } l_1 h_{\text {b}})^{1/2}\max \{1,{\gamma }\}^{-1/4} \end{aligned}$$

(6.53)

so that

$$\begin{aligned} E_{\text {BL}}^\eta \le l_2 ({\sigma } l_1 h_{\text {b}})^{1/2}\max \{1,{\gamma }\}^{3/4}. \end{aligned}$$

(6.54)

For each regime, it is easy to check that this boundary layer energy is no greater than the energy of the constructions given in Theorem 2.1. $\square$

This is the simplest possible modification of the proof of Theorem 2.1, and we do not claim that the bound $h_{\text {b}}/l_1 < \min \{{\sigma },{\sigma }^{-1} {{\gamma }}^{-3/2}\}$ is sharp.

Appendix 3: Poincaré Constant

In this section, we prove the Poincaré inequality (3.2). It is sufficient to prove the following:

Lemma 6.9

Let $Q=(0,1) \times (0,1)$ be the unit square and ${\varvec{f}}\in {W^{1,2}}(Q;{\mathbb {R}}^2)$. Let ${\varvec{f}}$ be zero on at least half of the square:

$$\begin{aligned} | \{ {\varvec{x}}\in Q : {\varvec{f}}({\varvec{x}}) = {\mathbf {0}} \}| \ge \frac{1}{2}. \end{aligned}$$

Then,

$$\begin{aligned} \int _Q |{\varvec{f}}|^2 \, d {\varvec{x}}\le \int _Q |D {\varvec{f}}|^2 \, d {\varvec{x}}. \end{aligned}$$

Proof

First we recall the Poincaré inequality in one dimension. Let ${\varvec{g}}\in C^1([0,1]; {\mathbb {R}}^2)$. Write ${\varvec{g}}$ as the Fourier cosine series (the Fourier series of the even extension of g to $[-1,1]$)

$$\begin{aligned} {\varvec{g}}(x) = \frac{{\hat{{\varvec{g}}}}_0}{2} + \sum _{k=1}^\infty {\hat{{\varvec{g}}}}_k \cos (\pi k x), \qquad {\hat{{\varvec{g}}}}_k = 2 \int _0^1 {\varvec{g}}(x) \cos (\pi k x) \, {\text {d}}x. \end{aligned}$$

Let $\overline{{\varvec{g}}} = {\hat{{\varvec{g}}}}_0/2 = \int _0^1 {\varvec{g}}(x) \, {\text {d}}x$. By Parseval’s Theorem

$$\begin{aligned} \int _0^1 |{\varvec{g}}(x) - \overline{{\varvec{g}}} |^2 \, {\text {d}}x= & {} \frac{1}{2} \sum _{k=1}^\infty |{\hat{{\varvec{g}}}}_k|^2 = \frac{1}{2 \pi ^2} \sum _{k=1}^\infty \frac{1}{k^2} |\pi k {\hat{{\varvec{g}}}}_k|^2 \le \frac{1}{2 \pi ^2} \sum _{k=1}^\infty |\pi k {\hat{{\varvec{g}}}}_k|^2\nonumber \\= & {} \frac{1}{\pi ^2} \int _0^1 |{\varvec{g}}'(x)|^2 \, {\text {d}}x, \end{aligned}$$

(6.55)

which is the Poincaré inequality in one dimension. By density, the same holds for ${\varvec{g}}\in W^{1,2}((0,1);{\mathbb {R}}^2)$.

We now turn to the two-dimensional case. By Fubini’s theorem, for almost every x one has ${\varvec{f}}(x,\cdot )\in W^{1,2}((0,1);{\mathbb {R}}^2)$. Let

$$\begin{aligned} {\varvec{a}}(x) = \int _0^1 {\varvec{f}}(x,y) \, {\text {d}}y, \qquad \overline{{\varvec{a}}} = \int _0^1 {\varvec{a}}(x) \, {\text {d}}x = \int _Q {\varvec{f}}(x,y) \, {\text {d}}x{\text {d}}y. \end{aligned}$$

By equation (6.55)

$$\begin{aligned} \int _0^1 |{\varvec{a}}(x) - \overline{{\varvec{a}}}|^2 \, {\text {d}}x\le & {} \frac{1}{\pi ^2} \int _0^1 |{\varvec{a}}'(x)|^2 \, {\text {d}}x \le \frac{1}{\pi ^2} \int _0^1 \int _0^1 |{\varvec{f}}_x |^2 \, {\text {d}}x{\text {d}}y,\\ \int _0^1 |{\varvec{f}}(x,y) - {\varvec{a}}(x)|^2 \, {\text {d}}y\le & {} \frac{1}{\pi ^2} \int _0^1 |{\varvec{f}}_y|^2 \, {\text {d}}y. \end{aligned}$$

Therefore,

$$\begin{aligned} \int _Q | {\varvec{f}}- \overline{{\varvec{a}}} |^2 \, {\text {d}}x{\text {d}}y\le & {} 2 \left( \int _Q | {\varvec{f}}- {\varvec{a}}|^2 \, {\text {d}}x{\text {d}}y + \int _Q | {\varvec{a}}- \overline{{\varvec{a}}} |^2 \, {\text {d}}x{\text {d}}y \right) \nonumber \\\le & {} \frac{2}{\pi ^2} \int _Q |D {\varvec{f}}|^2 \, {\text {d}}x{\text {d}}y. \end{aligned}$$

(6.56)

Let $U = \{ {\varvec{x}}\in Q : {\varvec{f}}({\varvec{x}}) = {\mathbf {0}} \}$. We have

$$\begin{aligned} \frac{1}{2} |\overline{{\varvec{a}}}|^2 \le |U| |\overline{{\varvec{a}}}|^2 = \int _U |{\varvec{f}}- \overline{{\varvec{a}}}|^2 \, {\text {d}}x \le \frac{2}{\pi ^2} \int _Q |D {\varvec{f}}|^2 \, {\text {d}}x{\text {d}}y. \end{aligned}$$

(6.57)

Observe that

$$\begin{aligned} \int _Q |{\varvec{f}}- \overline{{\varvec{a}}}|^2 \, d {\varvec{x}}= \int _Q |{\varvec{f}}|^2 \, d{\varvec{x}}- |\overline{{\varvec{a}}}|^2. \end{aligned}$$

By combining this with estimates (6.56) and (6.57), we obtain

$$\begin{aligned} \int _Q |{\varvec{f}}|^2 \, d {\varvec{x}}= \int _Q |{\varvec{f}}- \overline{{\varvec{a}}}|^2 \, d {\varvec{x}}+ |\overline{{\varvec{a}}}|^2 \le \frac{6}{\pi ^2} \int _Q |D {\varvec{f}}|^2 \, d {\varvec{x}}\end{aligned}$$

which, since $6<\pi ^2$, completes the proof. $\square$