Efficiency evaluation in data envelopment analysis using strong defining hyperplanes

Abstract

Cross-efficiency analysis in DEA generally uses a two-stage procedure: first, optimize a DMU’s individual efficiency score; next, push the efficiencies of all DMUs in a desired direction. In order to reduce subjective judgement in the second step, we provide a cross-efficiency method using only strong defining hyperplanes of the underlying technology. We develop a new DEA-based algorithm, and prove its finiteness and correctness. To reduce the computational burden, we show how one can combine the procedure with a known beneath-and-beyond procedure. Numerical investigations—comprising real-world data—demonstrate the superiority of the new method.

1 Introduction

Data envelopment analysis (DEA) is a meaningful instrument for evaluating the efficiencies of profit and non-profit entities, so-called decision-making units (DMUs), cf. Charnes et al. (1978). Here, a ratio of weighted outputs to weighted inputs for the observed activity of a DMU will be optimized to determine its CCR-efficiency; the acronym CCR stands for Charnes, Cooper, and Rhodes, of course. The second well-studied model is that of Banker, Charnes, and Cooper published in 1984. It informs a DMU about its pure technical efficiency, namely the BCC-efficiency, as well as its qualitative and quantitative returns to scale (RTS), calculating a slightly different fraction as in the CCR case. For more details on this refer to Banker et al. (1984), Førsund (1996), Kleine et al. (2016) or Podinovski et al. (2009).

However, one main feature of both classical approaches is that each DMU optimizes its individual fraction by choosing the most favorable weights; this is often called self-appraisal. To overcome this flaw, cross-efficiency evaluation has been developed as an alternative way of efficiency evaluation and, consequently, to rank all DMUs; see e.g., Doyle and Green (1994). In this framework, all individual weighting schemes are applied to the activities of all DMUs, resulting in a so-called cross-efficiency matrix. This matrix can be used to estimate the efficiency for a DMU calculating its average cross-efficiency.

Yet, the individually determined weights are generally ambiguous, this is also true for cross-efficiencies. Accordingly, a two-stage procedure is often applied to overcome this issue effectively: first, determine a DMU’s individual efficiency score; next, solve a second problem that pushes the efficiencies of all DMUs in a desired direction, but yet fix the efficiency score of the previously optimized DMU. However, the latter demands for an analyst’s philosophy: in what direction should we push all efficiencies—benevolent or aggressive?

In Wang and Chin (2010), the authors present an approach that is called a neutral DEA model for cross-efficiency evaluation; here, they seek for more neutral weights instead of applying benevolently or aggressively determined weights. However, their interpretation of a neutral DEA model seems flawed, because the authors control the choice of weights only from the viewpoint of the DMU which has been individually optimized in the first stage of the classical two-stage procedures. Consequently, this approach also has a rather subjective character. Furthermore, the proposed model does not guarantee that we use hyperplanes with maximal support by the underlying polyhedron. Consequently, the authors only gather little (almost arbitrary) information from the technology. This is also true for the neutral cross-efficiency concept presented in Carrillo and Jorge (2018); here, the authors formulate a new second-stage program, where hypothetical best- and worst-performing units must be specified.

We provide a new cross-efficiency method that corresponds to the term neutrality more than the classical procedures and the aforementioned concepts, applying all strong defining hyperplanes of the underlying technology or production possibility set and thus, eventually, mitigating potential conflicts associated with the analyst’s subjectivity and gathering more information from the technology. In summary, the new method neither requires a specification of hypothetical best- and worst-performing units like in Carrillo and Jorge (2018) nor has it the risk of focusing only on a few—probably strange—weight systems as in Wang and Chin (2010).

However, finding strong defining hyperplanes can be very expansive from a computational point of view. In DEA, there are some papers providing search processes to find all strong defining hyperplanes and most of them are based on DEA multiplier models; see Amirteimoori and Kordrostami (2012); Davtalab-Olyaie et al. (2014) or Jahanshahloo et al. (2009). In Davtalab-Olyaie et al. (2014) and Jahanshahloo et al. (2009), for example, the authors offer approaches which are mainly based on the BCC multiplier problem, but the algorithms proposed here require evaluating all extreme solutions and respective hyperplanes which can be very expensive. In Amirteimoori and Kordrostami (2012), the authors develop an approach using data perturbations. However, this method asks for a specification of respective perturbation parameters. In order to avoid these issues, we determine all strong defining hyperplanes, using DEA models, some combinatorics, and some plain algebraic concepts. Furthermore, we prove that the new procedure always terminates and, additionally, that it always finds all strong defining hyperplanes. Next, we combine DEA and a well-known beneath-and-beyond algorithm—namely QuickHull—to radically accelerate the search process; for details on beneath-and-beyond strategies see Joswig (2003). Computational experiments reveal the superiority of the new method.

The present contribution is organized as follows. In Sect. 2, we summarize some basics of DEA. The concept of cross-efficiencies and the relationship between this concept and strong defining hyperplanes is given in Sect. 3. In Sect. 4, we develop both algorithms for determining all strong defining hyperplanes; here, we compare the technical performance of both procedures, studying different scenarios for an empirical application of 125 adult education centers (AECs). The quality of the efficiency estimators of different approaches will be checked in Sect. 5, studying the empirical data of the 125 AECs again as well as performing a simulation study. Section 6 concludes the paper.

2 Preliminaries

Problems (1) and (2) show the classical BCC models in envelopment and multiplier form, cf. Banker et al. (1984). In the remainder of this study, we focus on input orientation, but the proposed framework can easily be transferred to other approaches as output orientation or slack-based models; for an overview cf. Cooper et al. (2007).

For all $k \in \mathcal {J}$, with $\mathcal {J} = \{1,...,J\}$, solve

$$\begin{aligned}&\min \theta _k \nonumber \\ s.t.& \quad \theta _k \mathbf{x}_k - \sum _j \lambda _{{kj}} \mathbf{x}_j \geqq \mathbf{0} \nonumber \\&\sum _j \lambda _{{kj}} \mathbf{y}_j \geqq \mathbf{y}_k \nonumber \\&\sum _j \lambda _{{kj}} = 1 \nonumber \\&\lambda _{{kj}} \geqq 0 \ \forall j \ \text {and} \ h_k \ \text {free} \end{aligned}$$

(1)

$$\begin{aligned}&\max {g}_{k} = \mathbf{U}_{k}^{\mathsf {T}} \mathbf{y}_{k} + {u}_{k} \nonumber \\ s.t.& \quad \mathbf{V}_{k}^{\mathsf {T}} \mathbf{x}_{k} = 1 \nonumber \\&\mathbf{U}_{k}^{\mathsf {T}}{} \mathbf{y}_{j} + {u}_{k} - \mathbf{V}_{k}^{\mathsf {T}}{} \mathbf{x}_{j} \leqq 0 \quad \forall j \nonumber \\&\mathbf{U}_{k}, \mathbf{V}_{k} \geqq \mathbf{0} \text { and } {u}_{k} \text { free. } \end{aligned}$$

(2)

($\mathbf{x}_j$, $\mathbf{y}_j$) $\in \mathbb {R}_+^{M+S}$ are the observed inputs and outputs or the activities of all DMUs; here, M stands for the number of inputs and S for the number of outputs. In the envelopment form (1), the efficiency will be captured via $\theta _k$; the production possibility set is then formed by observed activities, the respective intensities $\lambda _{{kj}}$ plus the convexity constraint. In the multiplier form (2), the efficiency will be determined by $g_k$; where $\mathbf{U}_k$, $\mathbf{V}_k$ are the vectors of output and input multipliers and ${u}_k$ is the free variable, which indicates the returns to scale situation of DMU k; see e.g., (Banker et al. 1984) and Førsund (1996). More precisely: if the optimal ${u}_k$, from now on indicated by a superscript star, is >/</$=0$, then DMU k operates under increasing/decreasing/constant returns to scale (IRS/DRS/CRS).

As discussed in Banker and Thrall (1992), Golany and Yu (1997), and Doyle and Green (1994), the linear program (2) might be subject to alternative optimal solutions. Therefore, in the aforementioned papers, the authors propose various two-stage procedures following different economic philosophies. Accordingly, let ${g}^*_k, \mathbf{U}^*_k, \mathbf{V}^*_k, {u}^*_k$ be an optimal solution of (2) for an arbitrary DMU k. In the first two manuscripts, the authors use (3) to fathom a DMU’s returns to scale situation; obviously, this leads to an interval for ${u}_k$.

$$\begin{aligned} \quad \quad&{u}^-_k = \inf {u}_k \text { or }{u}^+_k = \sup {u}_k \nonumber \\ s.t.& \quad \mathbf{V}_k^{\mathsf {T}} \mathbf{x}_k = 1 \nonumber \\&\mathbf{U}_k^{\mathsf {T}} \mathbf{y}_k + {u}_k = {g}^*_k \nonumber \\&\mathbf{U}_k^{\mathsf {T}}{} \mathbf{y}_j + {u}_k - \mathbf{V}_k^{\mathsf {T}}{} \mathbf{x}_j \leqq 0 \quad \forall j \nonumber \\&\mathbf{U}_k, \mathbf{V}_k \geqq \mathbf{0} \text { and } {u}_k \text { free } \end{aligned}$$

(3)

On the other hand, the latter paper focuses on the efficiency evaluations of the remaining DMUs; here, the authors force such evaluations into a desired direction, again under constant efficiency of DMU k. Consequently, we obtain (4).

$$\begin{aligned} \quad \quad \quad \quad \quad \quad&\min \sum _j{s}_{{kj}} \text { or } \max \sum _j{s}_{{kj}} \nonumber \\ s.t.& \quad \mathbf{V}_k^{\mathsf {T}} \mathbf{x}_k = 1 \nonumber \\&\mathbf{U}_k^{\mathsf {T}} \mathbf{y}_k + {u}_k = {g}^*_k \nonumber \\&\mathbf{U}_k^{\mathsf {T}}{} \mathbf{y}_j + {u}_k - \mathbf{V}_k^{\mathsf {T}}{} \mathbf{x}_j + {s}_{{kj}} = 0 \quad \forall j \nonumber \\&\mathbf{U}_k, \mathbf{V}_k \geqq \mathbf{0}, {s}_{{kj}} \geqq {0} \ \forall j \text { and } {u}_k \text { free } \end{aligned}$$

(4)

The linear program (4) guides immediately to the concept of cross-efficiency evaluation; the next section substantiates this statement.

3 From cross-efficiencies to strong defining hyperplanes

As already indicated, cross-efficiencies are the efficiencies of DMUs from the viewpoint of other DMUs, cf. Doyle and Green (1994). Again, let $\mathbf{U}^*_k, \mathbf{V}^*_k, {u}^*_k$ be an optimal weight system of a DMU k; cross-efficiencies are then defined by

$$\begin{aligned} g^*_{{kj}} = \frac{\mathbf{U}_k^{*\mathsf {T}}{} \mathbf{y}_j + {u}_k^{*}}{\mathbf{V}_k^{*\mathsf {T}}{} \mathbf{x}_j} \quad \forall \ k, j \in \mathcal {J}. \end{aligned}$$

(5)

Such cross-efficiencies can be arranged in a matrix ($g^*_{{kj}}$)$_{J,J}$, a cross-efficiency matrix. Using the classical cross-evaluation scheme for ranking all DMUs means determining the average cross-efficiency column-wise from the cross-efficiency matrix ($g^*_{{kj}}$)$_{J,J}$:

$$\begin{aligned} \frac{1}{J}\sum _kg^*_{{kj}} = \frac{1}{J}\sum _k\frac{\mathbf{U}_k^{*\mathsf {T}}{} \mathbf{y}_j + {u}_k^{*}}{\mathbf{V}_k^{*\mathsf {T}}{} \mathbf{x}_j} \ \forall j. \end{aligned}$$

(6)

Yet, what is the linking element between (4) and (5)? To answer this question, we need the affine equation

$$\begin{aligned} {\mathbf{U}_k^{*\mathsf {T}}{} \mathbf{y}_j + {u}_k^{*}}- g^*_{{kj}}{\mathbf{V}_k^{*\mathsf {T}}{} \mathbf{x}_j} = 0, \end{aligned}$$

(7)

which is called efficiency equation of DMU j at cross-efficiency level $g^*_{{kj}}$. Replacing $g^*_{{kj}}$ by $(1-\sigma ^*_{{kj}})$ in Eq. (7) we obtain

$$\begin{aligned} {\mathbf{U}_k^{*\mathsf {T}}{} \mathbf{y}_j + {u}_k^{*}}- (1-\sigma ^*_{{kj}}){\mathbf{V}_k^{*\mathsf {T}}{} \mathbf{x}_j} = 0. \end{aligned}$$

(8)

Compressing $\sigma ^*_{{kj}}{\mathbf{V}_k^{*\mathsf {T}}{} \mathbf{x}_j}$ to $s^*_{{kj}}$ and rearranging terms we have

$$\begin{aligned} {\mathbf{U}_k^{*\mathsf {T}}{} \mathbf{y}_j + {u}_k^{*}}- {\mathbf{V}_k^{*\mathsf {T}}{} \mathbf{x}_j} + s^*_{{kj}} = 0. \end{aligned}$$

(9)

When applying (4), we evenly push the cross-efficiencies in a particular direction: benevolent when minimizing and aggressive when maximizing the sum of all $s_{{kj}}$. The reference the cross-efficiencies are pushed away from or pushed towards is the supporting hyperplane

$$\begin{aligned} \text {H}_k \overset{\wedge }{=} {\mathbf{U}_k^{*\mathsf {T}}{} \mathbf{y} + {u}_k^{*}}- {\mathbf{V}_k^{*\mathsf {T}}{} \mathbf{x}} = 0. \end{aligned}$$

(10)

Solving (2) and (4) for an arbitrary k means determining a supporting hyperplane (10) that touches the respective BCC technology or production possibility set by at least one activity ($\mathbf{x}_j$, $\mathbf{y}_j$), i.e., at least one activity ($\mathbf{x}_j$, $\mathbf{y}_j$) $j \in \mathcal {J}$ is BCC cross-efficient from the perspective of DMU k.

Example 1

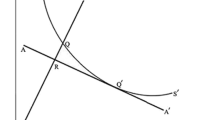
Figure 1 shows the classical BCC technology for 6 DMUs with a single input and a single output each. Here, we illustrate two arbitrary supporting hyperplanes $\text {H}_1$ and $\text {H}_3$ and the cross-efficiency projection point for DMU 4 on $\text {H}_1$, namely the supporting hyperplane from the perspective of DMU $k=1$. $\diamond$

Fig. 1

Arbitrary supporting hyperplanes and cross-efficiency projection

It is well-known that a supporting hyperplane (10) is a subspace of the real coordinate space $\mathbb {R}^{M+S}$, and it is of full-dimension if its dimension equals ${M+S}-1$. The intersection of such a hyperplane and respective BCC technology is called facet. In addition, we now present the following definitions, see Jahanshahloo et al. (2007):

Definition 1

If a supporting hyperplane $\text {H}_k$ passes through ${M+S}$ BCC efficient DMUs, which are affinely independent, then $\text {H}_k$ is a defining hyperplane.

This definition implies that when $\text {H}_k$ is a defining hyperplane, then $M+S$ DMUs are cross-efficient $g^*_{kl}=1$, with $l = j_1, \dots , j_{M+S}$, and their respective activities have to be affinely independent of each other.

Definition 2

If Definition 1 holds and, additionally, we have $(\mathbf{U}^*_k, \mathbf{V}^*_k) > \mathbf{0}$, then $\text {H}_k$ is a strong defining hyperplane.

To make the above concepts more transparent, we continue the example.

Example 2

In Fig. 2, one can see that $\text {H}_1$ is a defining hyperplane but not a strong defining one due to $\mathbf{U}^*_1 =0$. $\text {H}_3$ is just a supporting hyperplane, and not even a defining one, due to the fact that it only touches the activity of DMU 3. The two hyperplanes corresponding to the bold marked facets are the only available strong defining hyperplanes in this example, see Fig. 3. Here, the strong defining hyperplane $\text {H}_2$ is spanned via DMU 2 and DMU 3, the second one $\text {H}_4$ is constructed by DMU 3 and DMU 4. $\diamond$

Fig. 2

Supporting vs. defining hyperplanes

Fig. 3

Strong defining hyperplanes

However, applying Eqs. (2) and (3) or (4) only ensures that we use supporting hyperplanes to calculate cross-efficiencies (5) and the respective averages via (6), but it does not guarantee that these hyperplanes have any of the properties introduced in Definition 1 and Definition 2. From an analyst’s point of view, it might be more reasonable to assess a DMU’s average cross-efficiency with respect to all strong defining hyperplanes, because these hyperplanes are not degenerated and have maximal support by the underlying technology, i.e., by the empirical data points. This is the guiding principle for the subsequent developed approach.

Let $\mathcal {H}$ be the set of all strong defining hyperplanes and $|\mathcal {H}|$ its cardinality. Still, there could be several problems when focussing only on strong defining hyperplanes: First, if the technology is ill-conditioned, as discussed in Olesen and Petersen (1996), then there is no strong defining hyperplane $(\mathcal {H} = \emptyset )$ that can be used for analytical purposes. Therefore, in Olesen and Petersen (2015) a test for the existence of at least one strong defining hyperplane is presented. In the case of $\mathcal {H} = \emptyset$, the DEA database has been poorly selected and hence should be reviewed, see again (Olesen and Petersen 1996). Second, and more importantly, finding all strong defining hyperplanes can be a difficult and computationally expensive exercise. This is subject of the next section.

4 Finding all strong defining hyperplanes

4.1 A DEA-based procedure

Finding all strong defining hyperplanes (SDHs) is an important task in DEA. In order to illustrate this, Davtalab-Olyaie et al. (2014) provides a list of research topics and respective references where SDHs are of interest. However, to the best of our knowledge, there is no study that has paid any attention to cross-efficiency evaluation in this context. To fill in this gap, Definition 1 and Definition 2 offer the relevant information for finding all strong defining hyperplanes, applying only DEA models, some combinatorics, and some algebra. In doing so, the new DEA-based algorithm for determining all strong defining hyperplanes is as follows:

• Step 1: Solve problem (1) for all DMUs; let $\mathcal {J}^{{\mathrm{eff}}}$ be the set of (weak) efficient DMUs and $\mathcal {J}^{{\mathrm{ineff}}}$ be the set of inefficient DMUs.

• Step 2: Determine the set of all possible index combinations, where each combination includes $M+S$ different indices of $\mathcal {J}^{{\mathrm{eff}}}$. With $n:=|\mathcal {J}^{\mathrm{{eff}}}|$ being the cardinal number of the respective index set; obviously, there are $I:=\left( {\begin{array}{c}n\\ M+S\end{array}}\right) = \frac{n!}{(M+S)!\cdot (n-M-S)!}$ possible combinations. Let $\mathcal {I}$ be a matrix with I rows and $M+S$ columns.

• Step 3: Next, we delete each line i of $\mathcal {I}$, containing indices of affinely dependent activities. This can simply be checked by solving

  $$\begin{aligned} \begin{array}{ l c l c l c l} \lambda _{i_1}{} \mathbf{x}_{i_1} &{} + &{} \cdots &{} + &{} \lambda _{i_{M+S}}{} \mathbf{x}_{i_{M+S}} &{} = &{} 0\\ \lambda _{i_1}{} \mathbf{y}_{i_1} &{} + &{} \cdots &{} + &{} \lambda _{i_{M+S}}{} \mathbf{y}_{i_{M+S}}&{} = &{} 0\\ \lambda _{i_1} &{} + &{} \cdots &{} + &{} \lambda _{i_{M+S}}&{} = &{} 0 \\ \end{array} \end{aligned}$$

  If we only obtain the trivial solution $\lambda _{i_1} = \lambda _{i_2} = \dots = \lambda _{i_{M+S}} = 0$, then the respective activities are affinely independent; otherwise delete the corresponding row in $\mathcal {I}$. Let $\mathcal {I}^{\mathrm{red}}$ be the reduced index matrix with $I^{\mathrm{red}}$ lines.

• Step 4: The activities of an index combination (one row) of $\mathcal {I}^{\mathrm{red}}$ do not necessarily span a supporting hyperplane, i.e., the respective hyperplane may cut the technology. Therefore, for each row i of $\mathcal {I}^{\mathrm{red}}$, with $i = 1,\dots ,{I}^{\mathrm{red}}$, solve

  $$\begin{aligned}&{s}^-_i = \min \sum _j{s}^-_{{ij}} \nonumber \\ s.t.& \quad \mathbf{V}_i^{\mathsf {T}}{} \mathbf{x}_j = 1 \quad \text {arbitrary } j \in \mathcal {I}_i^{\mathrm{red}} \nonumber \\&\mathbf{U}_i^{\mathsf {T}}{} \mathbf{y}_j + {u}_i - \mathbf{V}_i^{\mathsf {T}}{} \mathbf{x}_j = 0 \quad \forall j \in \mathcal {I}_i^{\mathrm{red}} \nonumber \\&\mathbf{U}_i^{\mathsf {T}}{} \mathbf{y}_j + {u}_i - \mathbf{V}_i^{\mathsf {T}}{} \mathbf{x}_j + {s}^+_{{ij}} - {s}^-_{{ij}} = 0 \quad \forall j \nonumber \\&\mathbf{U}_i, \mathbf{V}_i \geqq \mathbf{0}, {s}^+_{{ij}}, {s}^-_{{ij}} \geqq {0} \ \forall j \text { and } {u}_i \text { free } \end{aligned}$$

  (11)

  If ${s}^-_i > 0$ or if at least one weight of the unique $\mathbf{U}^*_i, \mathbf{V}^*_i$ equals zero, then delete line i in $\mathcal {I}^{\mathrm{red}}$. Let $\mathcal {I}^{{\mathrm{fin}}}$ be the final index matrix, containing all $M+S$-tuples for ${I}^{{\mathrm{fin}}}$ strong defining hyperplanes.

The gist of this procedure will be illustrated via the already introduced example.

Example 3

From Sect. 3 we have learned that the algorithm should find two strong defining hyperplanes. Accordingly,

• Step 1: We solve the classical BCC problems for all six DMUs. The result is the index set $\mathcal {J}^{{\mathrm{eff}}} = \{1,\dots ,4\}$ of all (weak) efficient DMUs.

• Step 2: Next, we determine the matrix $\mathcal {I}$, containing all possible index combinations. In this particular case, we have $I:=\left( {\begin{array}{c}n\\ M+S\end{array}}\right) =\left( {\begin{array}{c}4\\ 2\end{array}}\right) = 6$ of such combinations:

  $$\begin{aligned} \mathcal {I}= \left( \begin{array}{ r r } 1 &{} 2 \\ 1 &{} 3 \\ 1 &{} 4 \\ 2 &{} 3 \\ 2 &{} 4 \\ 3 &{} 4 \\ \end{array} \right) \end{aligned}$$

• Step 3: Checking the activities pairwise for affine dependencies, we obtain the matrix $\mathcal {I}^{\mathrm{red}}$; in this particular case, we maintain the matrix of step 2:

  $$\begin{aligned} \mathcal {I}^{\mathrm{red}}= \left( \begin{array}{ r r } 1 &{} 2 \\ 1 &{} 3 \\ 1 &{} 4 \\ 2 &{} 3 \\ 2 &{} 4 \\ 3 &{} 4 \\ \end{array} \right) \end{aligned}$$

• Step 4: Now, solving (11) for $\mathcal {I}^{\mathrm{red}}$ leads to the correct index matrix for spanning the two strong defining hyperplanes:

  $$\begin{aligned} \mathcal {I}^{{\mathrm{fin}}}= \left( \begin{array}{ r r } 2 &{} 3 \\ 3 &{} 4 \\ \end{array} \right) \end{aligned}$$

  If we construct, for example, a hyperplane by DMU 1 and DMU 3, see the second line of $\mathcal {I}^{\mathrm{red}}$, then we cut the technology, i.e., ${s}^{*-}_2 > 0$ due to DMU 2; refer again to Fig. 2 or 3. For the hyperplane constructed by the DMUs 1 and 2, see the first line of $\mathcal {I}^{\mathrm{red}}$, we obtain a defining hyperplane with $\mathbf{U}^*_1 =0$; hence, the first line of $\mathcal {I}^{\mathrm{red}}$ must be eliminated as well. The remaining lines in $\mathcal {I}^{\mathrm{red}}$ must be checked analogously. $\diamond$

Proposition 1

The DEA-SDH algorithm always terminates.

Proof

The proof follows simply from the fact that a finite number of activities is considered, since this then implies that we have a finite number of (weak) efficient activities, and hence for the binomial coefficient it always holds that $I:=\left( {\begin{array}{c}n\\ M+S\end{array}}\right)<\!< \infty$. This ultimately means that the respective index matrix has a finite number of rows, which have to be checked iteratively without any loop. $\square$

Theorem 1

The DEA-SDH algorithm always finds all strong defining hyperplanes.

Proof

We prove this statement by contradiction for each of the four algorithm steps separately.

• Ad 1: A strong defining hyperplane can, per definition, only be spanned uniquely via $M+S$ affinely independent extreme vertices. This means: if there is a hidden strong defining hyperplane, the indices of all extreme vertices—only defined by observed activities—might not be fully determined in the first step. This, however, obviously contradicts the basic principle of DEA, see (1).

• Ad 2: A hidden strong defining hyperplane can occur when $\mathcal {I}$ does not contain all possible index pairs of strong defining hyperplanes. However, this can only be the case if $\mathcal {J}^{{\mathrm{eff}}}$ is incomplete, thus, again contradicting DEA; see once more (1).

• Ad 3: Due to Definition 1, defining and strong defining hyperplanes consist of affinely independent activities, meaning that the activity submatrices build up a system of equations which can only be solved trivially. Now, elimination of a line in $\mathcal {I}$ which corresponds to a submatrix of affinely independent activities contradicts the proposed procedure.

• Ad 4: A strong defining hyperplane implies that it supports the technology. Assuming now that $\exists {s}^-_{{ij}} > 0$, with $j \in \mathcal {J}$, such that ${s}^-_i > 0$ for an aribtrary strong defining hyperplane i contradicts the optimality of (11); the algorithm never deletes a strong defining hyperplane accidentally. However, the last statement does not ensure that only strong defining hyperplanes are detected so far. Finally, we have to check whether a defining hyperplane can happen to remain unrevealed, still. This cannot be the case because step 3 guarantees that all submatrices contain affinely independent activities. Consequently, each hyperplane—corresponding to an index pair in $\mathcal {I}^{\mathrm{red}}$—is uniquely defined. This implies that a defining hyperplane, which is not strong defining, has at least one zero weight and hence, the corresponding index tuple will always be erased.

$\square$

In Davtalab-Olyaie et al. (2015), the authors propose a mixed-integer programming-based algorithm to obtain all defining hyperplanes; they call them weak efficient full-dimensional facets. We can detect them as well, but without applying mixed-integer programming:

Corollary 1

If the last if-then condition (step 4) concerning the weights $\mathbf{U}^*_i, \mathbf{V}^*_i$ is omitted, then the algorithm finds all defining hyperplanes—including all strong defining hyperplanes, of course.

Proof

The proof follows the same logic as for Theorem 1, but without claiming to delete a hyperplane in the fourth step if it is constructed by at least one zero weight. $\square$

Once all hyperplanes of interest are detected via the new approach(es), we can determine the cross-efficiencies regarding each i-th hyperplane:

$$\begin{aligned} g^*_{{ij}} = \frac{\mathbf{U}_i^{*\mathsf {T}}{} \mathbf{y}_j + {u}_i^{*}}{\mathbf{V}_i^{*\mathsf {T}}{} \mathbf{x}_j} \quad \forall j \in \mathcal {J}. \end{aligned}$$

(12)

Calculating (12) for DMU $j \in \mathcal {J}$ and for $i=1,\dots ,I^{\mathrm{fin}}$, we get

$$\begin{aligned} {\overline{g}}^*_{j} =\frac{1}{I^{\mathrm{fin}}}\sum _{i=1}^{I^{{\mathrm{fin}}}} g^*_{{{ij}}} = \frac{1}{I^{{\mathrm{fin}}}}\sum _{i=1}^{I^{{\mathrm{fin}}}} \frac{\mathbf{U}_i^{*\mathsf {T}}{} \mathbf{y}_j + {u}_i^{*}}{\mathbf{V}_i^{*\mathsf {T}}{} \mathbf{x}_j}, \end{aligned}$$

(13)

namely the average SDH cross-efficiency of DMU j.

Remark 1

In DEA there is a wide range of literature dealing with so-called weight restrictions to obtain more reasonable technologies; for more details on this topic refer to Dellnitz (2016), Dyson and Thanassoulis (1988), Kuosmanen and Post (2001), and Podinovski and Bouzdine-Chameeva (2015). It is a well-known simple fact that when embedding such constraints, the corresponding dual procedure then adds virtual activities to the input/output database. Consequently, the here proposed new algorithm to obtain all strong defining hyperplanes is also applicable in the presence of weight restrictions, calculating BCC problems for the virtual activities and updating respective index sets, if necessary.

According to the remark, if the technology is improperly shaped, then one can add weight restrictions to achieve a more reasonable technology. In this case, the algorithm remains unchanged; we just add the corresponding virtual activities to our activity set and run the algorithm as provided in Sect. 4.2. Using a BCC model sometimes leads to negative cross-efficiencies, for example. For a geometric interpretation of negative cross-efficiencies see Lim and Zhu (2015); they show that negative cross-efficiencies can be related to free lunch or free production of outputs. In order to avoid such unreasonable evaluations, one can incorporate weight restrictions as proposed in Wu et al. (2009). The dual of the more constrained problem then discloses the requisite virtual activities to feed the algorithm.

4.2 First computational results

In general, educational efficiency is important for the overall prosperity of a country. This is confirmed by the large number of publications, dealing with DEA in this field of research; for a broad overview with respect to educational efficiency see De Witte and López-Torres (2017).

To show the computational performance of the new method, we study 125 public facilities, so-called Adult Education Centers (AECs), which are part of Germany’s educational landscape. The more than 900 of these institutions in Germany are organized into 16 associations, one association per state, which are subordinated to one umbrella association. Measuring the efficiency of such AECs is a complex task due to their non-profit status and the fact that education is not an instantenous phenomeon but shows its effects over the medium term. However, for demonstration purposes, we consider three inputs:

• Full-time equivalents (FT) of main educational staff (permanent contract)

• Full-time equivalents (PT) of part-time educational staff (avocational staff)

• Full-time equivalents (FT) of administrative staff

and two outputs:

• Number of regular course hours

• Number of one-off events

We restrict our analysis to the 125 AECs related to the association of North Rhine-Westphalia, the most densely populated federal state of Germany. This ensures that all AECs are subject to the same local regulations and the same environmental conditions. Table 1 displays some descriptive statistics for the business year 2013. In addition, we give correlations among the considered inputs and outputs in Table 2. All calculations were done on a Windows 10 PC, using MATLAB R2018b (64-bit).

Table 1 Descriptive statistics for 125 AECs

Table 2 Correlations between inputs and outputs

First, we focus on the two educational staff inputs and one output (the course hours) to visualize the results. Performing the DEA-based algorithm, we obtain 8 strong defining hyperplanes in approximately 15.703 seconds. Figure 4 illustrates the facets which correspond to the determined strong defining hyperplanes. Figure 5 presents the histogram of the average cross-efficiencies using (13). Here, the horizontal axis shows the respective average cross-efficiencies and the ordinate axis the number of DMUs (Figs. 6, 7, 8).

Fig. 4

Facets corresponding to all SDHs

Fig. 5

Histogram of the average cross-efficiencies

Next, we consider the first two inputs and both outputs. In this case, the computational time to find the 37 strong defining hyperplanes increases significantly (440.4585 seconds). This deterioration is primarily due to an increasing number of (weak) efficient DMUs (from $n_1 = 20$ to $n_2 = 31$) and, consequently, an exploding binomial coefficient; the latter increases from $I_1:=\left( {\begin{array}{c}n_1\\ 3\end{array}}\right) = 1140$ to $I_2:=\left( {\begin{array}{c}n_2\\ 4\end{array}}\right) = 31465$. This leads to the question: is there a less time-consuming way to obtain the same results? The next section answers this question.

4.3 Speed up by combining DEA and QuickHull

Finding the convex hulls of polyhedra is a topic investigated in-depth in mathematics, especially in combinatorial geometry and in operations research. One of the most prominent procedures for generating such convex hulls is called beneath-and-beyond (see again Joswig 2003), working incrementally via progressively adding points to an already constructed convex hull. Here, one powerful implementation is QuickHull, which is also made available by MATLAB. For further details regarding QuickHull refer to Barber et al. (1996) or Olesen and Petersen (2015). The latter authors use QuickHull to study marginal rates of substitution of DEA facets. When using QuickHull, we obtain the indices of all facets of the underlying polyhedron. The next figure shows the outcome for the three-dimensional case as introduced in Sect. 4.2:

Fig. 6

Convex hull for the AECs with two inputs and one output

Now, we combine our DEA-based algorithm and QuickHull to ultimately obtain the same information as provided in the Sects. 4.1 and4.2. The modified procedure comprises the following steps:

• Step 1: Solve problem (1) for all DMUs; let $\mathcal {J}^{{\mathrm{eff}}}$ be again the set of (weak) efficient DMUs and $\mathcal {J}^{{\mathrm{ineff}}}$ be the set of inefficient DMUs.

• Step 2: Determine the QuickHull index matrix $\mathcal {I}^{\mathrm{QHull}}$ with $I^{\mathrm{QHull}}$ rows and $M+S$ columns.

• Step 3: Next, delete each line of $\mathcal {I}^{\mathrm{QHull}}$, containing indices of inefficient activities. Let $\mathcal {I}^{\mathrm{del}}$ be the reduced matrix with $I^{\mathrm{del}}$ rows.

• Step 4: Now, for each row i of $\mathcal {I}^{\mathrm{del}}$, with $i = 1,\dots ,I^{\mathrm{del}}$, solve

  $$\begin{aligned}&{s}^-_i = \min \sum _j{s}^-_{{ij}} \nonumber \\ s.t.& \quad \mathbf{V}_i^{\mathsf {T}}{} \mathbf{x}_j = 1 \quad \text {arbitrary } j \in \mathcal {I}_i^{\mathrm{del}} \nonumber \\&\mathbf{U}_i^{\mathsf {T}}{} \mathbf{y}_j + {u}_i - \mathbf{V}_i^{\mathsf {T}}{} \mathbf{x}_j = 0 \quad \forall j \in \mathcal {I}_i^{\mathrm{del}} \nonumber \\&\mathbf{U}_i^{\mathsf {T}}{} \mathbf{y}_j + {u}_i - \mathbf{V}_i^{\mathsf {T}}{} \mathbf{x}_j + {s}^+_{{ij}} - {s}^-_{{ij}} = 0 \quad \forall j \nonumber \\&\mathbf{U}_i, \mathbf{V}_i \geqq \mathbf{0}, {s}^+_{{ij}}, {s}^-_{{ij}} \geqq {0} \ \forall j \text { and } {u}_i \text { free } \end{aligned}$$

  (14)

  Again, if ${s}^-_i > 0$ or if at least one weight of the unique $\mathbf{U}^*_i, \mathbf{V}^*_i$ equals zero, then we delete line i in $\mathcal {I}^{\mathrm{del}}$. Eventually, $\mathcal {I}^{{\mathrm{fin}}}$ is the final index matrix, containing only index pairs of strong defining hyperplanes.

The roots of QuickHull date back to the late 1970s; its name stems from Preparata and Shamos, refer to Preparata and Shamos (1985). It is proven that this algorithm detects the full convex hull of a polyhedron, see e.g., Barber et al. (1996). From the perspective of DEA this means that we obtain all extreme points on the convex hull, containing efficient as well as inefficient DMUs. More importantly, the QuickHull algorithm does not only search for strong defining hyperplanes. In fact, we obtain all extreme points on the convex hull, regardless of whether the activities are spanning either a strong defining hyperplane or just a defining hyperplane. Consequently, we need the additional calculations (Steps 3 and 4) in the combined algorithm. Due to the latter elimination steps and the fact that the DEA-SDH algorithm is proven to be correct, we can say that both algorithms must lead to the same part of the efficient boundary.

Now comparing both procedures, we have a clear picture: the combined version outperformes the DEA-driven algorithm significantly. The impressive numbers for the 125 AECs are summarized in Table 3:

Table 3 Performance comparison

Computational performance is only one important issue, but a further key question has to be addressed: why is the present concept more dispassionate or superior to other approaches? The next section stresses this point.

5 Increasing objectivity via (strong) defining hyperplanes

5.1 Discussion of the neutral concept of Wang and Chin

As already mentioned in the introduction, the authors in Wang and Chin (2010) also develop a neutral cross-efficiency concept. In order to assess more precisely the disadvantages of their two-stage approach compared with our method, we provide the equations as given in Wang and Chin (2010). The first stage of their approach is based on the classical CCR model (15), see also Charnes et al. (1978); from now on, we change from vector to sigma notation to make the concept more transparent.

$$\begin{aligned}&\max {g}_{k} = \sum ^S_{s=1}{u}_{{sk}}{y}_{{sk}} \nonumber \\ s.t.& \quad \sum ^M_{m=1}{v}_{{mk}}{x}_{{mk}} = 1 \nonumber \\&\sum ^S_{s=1}{u}_{{sk}}{y}_{{sj}} - \sum ^M_{m=1}{v}_{{mk}}{x}_{{mj}} \leqq 0 \quad \forall j \nonumber \\&{u}_{{sk}}, {v}_{{mk}} \geqq {0} \ \forall s, m \end{aligned}$$

(15)

Let ${g}^{**}_{k}$ be the optimal CCR-efficiency regarding (15). Next, the authors provide the fractional optimization problem (16).

$$\begin{aligned}&\max \ \delta = \min \ \bigg \{ \frac{{u}_{1k}{y}_{1k}}{\sum ^M_{m=1}{v}_{{mk}}{x}_{{mk}}}; \dots ;\frac{{u}_{{Sk}}{y}_{{Sk}}}{\sum ^M_{m=1}{v}_{{mk}}{x}_{{mk}}} \bigg \} \nonumber \\ s.t.& \quad \sum ^M_{m=1}{v}_{{mk}} \bigg (\sum ^J_{j=1}{x}_{{mj}}\bigg ) = 1 \nonumber \\&\frac{\sum ^S_{s=1}{u}_{{sk}}{y}_{{sk}}}{\sum ^M_{m=1}{v}_{{mk}}{x}_{{mk}}} = {g}^{**}_k \nonumber \\&\frac{\sum ^S_{s=1}{u}_{{sk}}{y}_{{sj}}}{\sum ^M_{m=1}{v}_{{mk}}{x}_{{mj}}} \leqq 1 \quad \forall j \ne k \nonumber \\&{u}_{{sk}}, {v}_{{mk}} \geqq {0} \ \forall s, m \end{aligned}$$

(16)

When considering (16), we see that the authors use a Chebyshev distance in order to push the efficiency configuration of DMU k as much as possible. This means that the authors seek for a new composition of DMU k’s CCR-efficiency (${g}^{**}_{k}$) regardless of the cross-efficiency compositions of the other DMUs. Ultimately, the authors use the optimal solutions of the above nonlinear problem to calculate the cross-efficiencies of all DMUs. As a consequence, their neutral concept is mainly driven by DMU k; hence, this concept follows more a philosophy as in classical self-appraisal. Furthermore, the authors only apply their concept to CCR models because BCC formulations like in (17) can be unbounded due to the free variable ${u}_k$, which limits the model’s usability significantly.

$$\begin{aligned}&\max \ \delta = \min \ \bigg \{ \frac{{u}_{1k}{y}_{1k}}{\sum ^M_{m=1}{v}_{{mk}}{x}_{{mk}}}; \dots ;\frac{{u}_{{Sk}}{y}_{{Sk}}}{\sum ^M_{m=1}{v}_{{mk}}{x}_{{mk}}} \bigg \} \nonumber \\ s.t.& \quad \sum ^M_{m=1}{v}_{{mk}} \bigg (\sum ^J_{j=1}{x}_{{mj}}\bigg ) = 1 \nonumber \\&\frac{\sum ^S_{s=1}{u}_{{sk}}{y}_{{sk}}+{u}_k}{\sum ^M_{m=1}{v}_{{mk}}{x}_{{mk}}} = {g}^{*}_k \nonumber \\&\frac{\sum ^S_{s=1}{u}_{{sk}}{y}_{{sj}} +{u}_k}{\sum ^M_{m=1}{v}_{{mk}}{x}_{{mj}}} \leqq 1 \quad \forall j \ne k \nonumber \\&{u}_{{sk}}, {v}_{{mk}} \geqq {0} \ \forall s, m \text { and } {u}_k \text { free;} \end{aligned}$$

(17)

where ${g}^{*}_k$ is the optimal efficiency of BCC problem (2).

A further problem is that their model always produces efficiency scores even if the technology is ill-conditioned, as discussed in Sect. 3 or in Olesen and Petersen (1996). In such a degenerated case, the optimal weight vectors often or always consist of at least one zero weight. From an economic point of view, zero weights pose a problem: such a weight implies that the corresponding input or output is unessential. Our approach informs the analyst if the technology is ill-conditioned, i.e., if we have no or only a few (strong) defining hyperplanes. Furthermore, our approach does not favor any specific weight composition; here, we gather all essential information of the production possibility set. Additionally, our method can be applied to different technologies (like constant, non-decreasing or non-increasing returns to scale) by adding virtual activities in the QuickHull input data or simply via changing the models in the DEA-based procedure proposed in Sect. 4.1. For the CCR case, we give the following remark:

Remark 2

As is well known, using a CCR model means to envelop all decision-making units in a convex cone. Consequently, every CCR SDH consists of $M+S-1$ efficient DMUs plus the zero point. To realize this, we can add the zero point to our data matrix and then passing it on to the DEA-based QuickHull algorithm (Step 2 of our combined procedure).

The next section studies the results of different approaches to underpin our statements.

5.2 Comparative results and reasoning

Here, we compare the results between the Wang and Chin approach and the new cross-efficiency method, studying the 125 AECs with three inputs and two outputs in a CCR technology. In doing this, we make use of Remark 2.

The following two figures (Figs. 7 and 8) show the average cross-efficiencies for the neutral model (16) of Wang and Chin and the CCR SDH approach; where again the horizontal axis displays the average cross-efficiencies and the ordinate axis the number of DMUs.

Fig. 7

Cross-effs via model (16)

Fig. 8

Cross-effs using CCR SDHs

The two distributions look pretty similar: they are both unimodal and approximately symmetric, the skewness of the left distribution equals 0.3788 and the skewness of the right is 0.4218. Interestingly, the kurtosis of each distribution is close to 3, which means that the shapes are nearly normal; the kurtosis of the left distribution equals 2.7797, and for the right one it is 2.9191. The average and maximum cross-efficiency of the CCR SDH model are higher (0.5827, 0.9475) than those of the approach of Wang and Chin (0.5771, 0.9167).

When taking a closer look at the underlying weight systems, then we recognize that the production possibility set is enveloped by 28 strong defining hyperplanes. Applying the approach of Wang and Chin, we obtain 125 weight systems to determine all cross-efficiencies. However, from these 125 weight systems, only 64 weight systems are unique and 34 of them are non-degenerated weight systems. Surprisingly, we get at least 24 of the 28 SDHs, but on the other hand, we neglect the information of 4 SDHs, i.e., 4 weight systems, which also contain important information of the production possibility set. To say it more clearly: In our context, the cross-efficiency assessments via the neutral model of Wang and Chin are based on 24 out of the 28 SDHs. This means that the weight systems are either orthogonal to these 24 SDHs or only touch one of these facets. However, the remaining 4 SDHs are totally disregarded when applying the model of Wang and Chin.

Now, analyzing the 125 AECs in the presence of a BCC model, we obtain the following average cross-efficiency distributions, where the horizontal axis again shows the average cross-efficiencies and the ordinate axis the number of DMUs. Here, Fig. 9 illustrates the average cross-efficiencies for the new approach, applying 93 strong defining hyperplanes; Fig. 10 provides the benevolent average cross-efficiencies, maximizing Eq. (4).

Fig. 9

Cross-effs using BCC SDHs

Fig. 10

Benevolent Cross-effs

Unsurprisingly, a comparison of the two figures shows that the benevolent method leads to a more dense distribution and higher averages than the new method. The overall averages illustrate this point even more clearly: in the BCC SDH case, we obtain 0.5214; in the benevolent case, we have 0.5608. Furthermore, the histogram in Fig. 10 exhibits a right-skewed form, which means that there are more AECs (namely 73) with an average cross-efficiency below of 0.5 than in the benevolent case (only 45 AECs).

If we try to compute (17), two of the 125 optimization problems are unbounded and 45 weight systems lead to negative cross-efficiencies. We eliminate these negative cross-efficiencies adding $\mathbf{U}_{k}^{\mathsf {T}}{} \mathbf{y}_{j} + {u}_{k} \geqq 0 \ \forall j$ in (2) and (17), see Wu et al. (2009); with these additional restrictions (17) is always bounded. After eliminating such 45 weight systems, we obtain the cross-efficiency histogram illustrated in Fig. 11. As mentioned above, the BCC production possibility set comprises 93 SDHs; however, model (17) just uses 17 out of the 93 SDHs to evaluate all DMUs, which means that the model (17) gathers only little information of the whole technology in this particular case.

Fig. 11

Cross-effs via the BCC model (17)

It is the first time that Adult Education Centers undergo a DEA-driven efficiency analysis. From a global perspective it becomes apparent that major parts of the 125 AECs are inefficient—no matter what model we prefer. On average, the savings potential with regard to both the administration and the teaching staff is approx. 40%. Unfortunately, such a dissipation is unacceptable for a country because the services of AECs are financed by more than 60% by public and local authorities. In particular, this demonstrates that measuring such educational efficiency is an important task, but often we do not know the correct underlying technology. From a technical perspective, still, it is an open question whether the new procedure leads to more reasonable and reliable estimations than the classical methods. More on that in the next section.

5.3 Reasonable efficiency estimations via SDHs: a simulation study

In order to answer the question, which has been raised previously, we perform a simulation study applying bootstrapping à la Simar and Wilson; for more details on this refer to Simar and Wilson (1998). Here, we assume a function of type Cobb-Douglas as a benchmark to calculating the true efficiencies; that is, first, we solve

$$\begin{aligned}&\min \ {\sum ^J_{j=1}{\epsilon }^2_{j}} \nonumber \\ s.t.& \quad \tilde{y}_{1j} - \alpha - {\sum ^M_{m=1}{\beta }_{m}\tilde{x}_{\mathrm{mj}}}+\gamma \tilde{y}_{2j} - \epsilon _j = 0 \quad \forall j \nonumber \\&\gamma , \beta _{m} \geqq {0} \ \forall m, \ \alpha \text { and } {\epsilon }_j \text { free in sign} \ \forall j; \end{aligned}$$

(18)

where $\tilde{y}_{{sj}}, \ \tilde{x}_{{mj}}$ are the logarithmized outputs and inputs, $\alpha ,\ \gamma , \ \beta _{m}$ are the functional parameters to be estimated, and $\epsilon _j$ are respective error terms, which are supposed to be independent normally distributed. Next, we apply an affine transformation in order to obtain an efficiency frontier, as done in corrected ordinary least squares (COLS); cf. e.g., Greene (2008) and Richmond (1974). Thus, let $\alpha ^*, {\gamma }^*,\ {\beta }^*_{m},\ {\epsilon }^*_j \ \forall m,\ j$ be the optimal solution regarding (18). Then the efficiency equation for each DMU is given by $\tilde{y}_{1j} = {\hat{\alpha }} + {\sum ^M_{m=1}{{\hat{\beta }}}_{m}\tilde{x}_{{mj}}}-{\hat{\gamma }} \tilde{y}_{2j} + {\hat{\epsilon _j}}$, with $\hat{\alpha }:={\alpha }^*+\max _j\{{\epsilon }^*_j\}, \hat{\gamma }:={\gamma }^*,\ \hat{\beta }_{m}:={\beta }^*_{m},$ and ${{\hat{\epsilon }}}_j := {\epsilon }^*_j-\max _j\{{\epsilon }^*_j\} \ \forall m,\ j$; now, the true efficiencies are simply determined via ${\hat{g}}_j = e^{-{{\hat{\epsilon }}}_j} \ \forall j$.

Due to the affine transformation and the fact that the Cobb-Douglas specification (18) leads to an R squared of nearly 0.8712, we check the methods assuming that a BCC technology better approximates the underlying functional relationship than the CCR case does. The simulation procedure now comprises the following steps:

• Step 1: The simulation is based on $N=7$ scenarios; in each scenario ($n=1,\ \dots ,\ N$), we generate different numbers of virtual activities via bootstrapping, namely $J_1 = 100,\ J_2 = 200,\ J_3 = 300,\ J_4 = 400,\ J_5 = 500,\ J_6 = 600,\ J_7 = 700$.

• Step 2: Each scenario of the simulation consists of 1000 iterations. In doing so, we draw $J_n$ activities at random from the set $\{(\mathbf{x}_j$, $\mathbf{y}_j)\}$ and from the set of efficiencies $\{{\hat{g}}_j\}$ in each iteration. To construct a virtual activitiy, we fix the outputs of the randomly drawn activitiy but divide respective inputs by a randomly drawn efficiency. Consequently, in the latter scenario, for example, we generate 1000 times 700 virtual activities.

• Step 3: Next, in each iteration, we estimate the true efficiencies of all virtual activities using the translated coefficients of (18). Additionally, we compute the efficiency scores of the virtual activities applying the classical BCC model (2), the benevolent version of (4), and the new SDH approach; we refrain from solving (17) due to the flaws revealed in Sect. 5.1.

• Step 4: Ultimately, we calculate the euclidean distances between the true efficiencies and the DEA-based efficiency scores. In each scenario and iteration, we get $J_n$ true efficiencies and $J_n$ efficiency estimates per model; such vectors are the basis for calculating distances over all 1000 iterations.

The relative performance between the methods are summarized in Table 4.

Table 4 Relative performance measures of the simulation

The second column displays the relative performance of the SDH method versus the BCC model. In the first scenario comprising $J_1 = 100$ virtual activities, the SDH approach better approximates the true efficiencies than the BCC model in 86.9% of the 1000 iterations; this implies that the SDH method leads to smaller distances in 869 iterations. The last column presents the relative outperformance (e.g., 54.8% in the first scenario) of SDH over the benevolent cross-evaluation. Obviously, SDH is superior to the benevolent cross-efficiency approach; and this outperformance is pretty stable over all seven scenarios. Interestingly, based on our simulation, we can conclude that one should prefer the SDH-based cross-efficiency analysis.

In general, one should use as much information as possible to assess profit or non-profit entities. This is important, inter alia, in order to mitigate the influence of outlier institutions. Choosing the right model is difficult due to the fact that it depends on the corresponding economic situation, which is subject to many uncertainties. As consequence, if the economic situation is rather ambiguous, one should prefer the SDH concept proposed for the following reasons:

• It is a more dispassionate concept because choosing an optimization philosophy or objective function as shown in (3), (4) or (16) becomes obsolete.

• It processes and embeds in general more information of the production possibility set than provided by (3), (4) or (16).

• It immediately reveals deficiencies of the underlying technology.

• Due to the second bullet point, the new SDH method can lead to more reasonable efficiency estimations, as demonstrated in the simulation study.

6 Conclusions and the road ahead

In this paper, we show how one can determine all strong defining hyperplanes (SDHs) in data envelopment analysis (DEA) using only DEA models. However, the computational time of this approach is rather poor and can be radically accelerated by combining DEA with a well-known beneath-and-beyond implementation called QuickHull. The strong defining hyperplanes are then applied to calculate the average cross-efficiencies and, hence, to determine more objective efficiency estimates than proposed by classical cross-efficiency evaluation frameworks. However, the question whether the new estimates are more reasonable and reliable from an economic perspective than those of classical procedures might be an interesting issue for empirical research. A first step in this direction has been taken applying a bootstrapping-based simulation. In this study, the new method significantly outperformed the efficiency approximations of the classical methods.