Introduction

Very often during the course of polymerisation processes, the viscosity of the reaction medium changes. When these changes significantly influence the polymerisation process rate, it becomes necessary to take into account these variables in balance equations describing this process. The need to take into account changes in viscosity means that systems of mass balance equations describing the polymerisation process are usually quite complex, and often difficult to solve due to the large number of unknown kinetic parameters. In connection with difficulties in determining polymerisation process kinetic parameters, the literature often assumes the same value for all constant rates of these reactions (k = const), and the effect of viscosity changes on the numerical values of the k constants is ignored. These methods are appropriate for systems, where viscosity is practically constant.

This paper attempts to take into account the effect of the increasing viscosity of the reaction medium on the kinetics of the linear polymer creation process occurring during polyaddition process. The increase in viscosity caused by the course of this process makes the constant reaction rate numerical values decrease, and, as such, may have a significant effect on the results.

Due to the complexity of the mass balance equation system and the necessity to take into account viscosity changes in numerical calculations, this paper uses the concept of partial reaction rate constants, the introduction of which into the balance equations allows a meaningful simplification of the mathematical model describing the polyaddition process being considered here. The influence of viscosity on the polymerisation rate has been taken into account by associating that rate with the number-average molecular mass M n of the reaction mixture, which provided an opportunity to associate kinetic parameters k with the number-average molar mass M n and—as a consequence—with the reaction mixture viscosity. Using the derived mass balance system of equations, which takes into account viscosity changes on the reaction rate constant numerical values, kinetic parameter values for the analysed processes were determined.

The proposed method facilitates the determination of partial reaction rate constant numerical values, and thus, it assists the progress of polymerisation kinetic parameters definition, which facilitates the system of balance equations to be solved.

Discussion of the process and the laboratory results

This work is based on empirical research described in paper [1], and its results were used to verify the proposed model of polymerisation.

The heteropolyaddition process analysis was carried out based on the literature data describing the bulk polyaddition process of diphenyl carbonate and bisphenol A diglycidyl ether in a batch reactor with ideal mixing at temperature t 1 = 100 °C and in time of 48 h [1]. The mechanism of the polyaddition reaction of diphenyl carbonate and bisphenol A diglycidyl ether producing polycarbon, depicted by the authors of this paper, proceeds in accordance with the equation presented in Fig. 1.

Fig. 1
figure 1

The mechanism of the heteropolyaddition reaction of diphenyl carbonate (a) and diglycidyl ether of bisphenol A (b) producing polycarbon (AB) n [1]

Full size image

To associate the heteropolyaddition process under analysis with the proposed model (in the latter part of the paper), the following designations for the reaction mixture have been adopted: diphenyl carbonate as A, diglycidyl ether of bisphenol A as B.

The reaction mixture was prepared by mixing 0.341 g (1.0 mmol) of bisphenol A diglycidyl ether and 0.214 g (1.0 mmol) of diphenyl carbonate in presence of 0.012 g (0.004 mmol) of tetrabutylphosphonium chloride (TBPC) as a catalyst and chlorobenzene (1.0 mol/l) as a solvent. The authors tabulated the obtained results in the form of the monomer conversion degree relationship and number-average molar mass M n relationship with the diphenyl carbonate and bisphenol A diglycidyl ether heteropolyaddition was correlated with the process time (at temperature t 1 = 100 °C).

As a result of the research conducted on the heteropolyaddition process described in paper [1], the authors achieved a conversion rate of 98 % (0.540 g) in 48 h. The number-average molar mass was M n = 28,300 g/mol for the reaction time equal to 48 h, whereas the mass-average molar mass and number-average molar mass ration was M w/M n = 1.89. During the initial 10–15 h of the reaction, number-average molar mass was increasing much more rapidly than in the latter stage of the heteropolyaddition process. At the same time, in the initial phase of the process, practically, the entire monomer mass is used, reaching, after just few hours, a 98 % monomer conversion rate after which it remains practically the same until the end of the heteropolyaddition process.

In the latter stage, the diphenyl carbonate and bisphenol A diglycidyl ether heteropolyaddition occurs with the use of tetrabutylphosphonium chloride as catalyst. Heteropolyaddition process literature [1] data were used to determine the process kinetic parameters.

The proposed model

The literature data [1] show that in real systems, very often during the course of polymerisation processes, the viscosity of the reaction medium changes. When the viscosity changes significantly influence the polymerisation process rate, it becomes necessary to take into account these variations in rate equations describing this process. A change in the viscosity of a reaction system, most often exhibiting itself by a change in the numeric kinetic value (which determines the rate of reaction), causes a reduction in the reaction rate numerical constants, which should be taken into consideration in numeric calculations. Changes in viscosity, during the course of a polymerisation process, cause a change in the process kinetic parameters, resulting in adding significant complexity to the mass balance equation system. As reaction rate constant values change with the progress of the polymerisation process, it becomes necessary, from the point of view of numeric calculations, to determine the reaction rate values at each step of the said calculations.

For a second-order reaction, the rate of which is expressed as \(r_{i} = k_{\text{AB}} C_{\text{A}} C_{\text{B}}\), the reaction rate constant is k AB. This value is related to the reaction and not to the reagent. In looking to associate the rate of reaction not with the reaction but reagent [2], this paper used the concept of partial reaction rate constant, replacing the reaction rate constant by a product of partial reaction rate constants as shown below:

$$k_{\text{AB}} = k_{\text{A}} k_{\text{B}}$$
(1)

The constants k A and k B in Eq. (1) (assigned to appropriate reagents, A and B) are called partial reaction rate constants, and their product is equal to reaction rate constant k AB [3, 4]. Using the partial reaction rate constant concept facilitates a formulation of a rate reaction depicting the rate of the second-order reaction as:

$$r_{i} = k_{\text{A}} k_{\text{B}} C_{\text{A}} C_{\text{B}}$$
(2)

However, Eq. (2) is much more conducive to numeric calculations and provides an opportunity to connect kinetic parameters with reaction medium viscosity changes.

In a sense, the partial reaction rate constants k A and k B characterise the rate of reaction of the given reagents A and B in the reaction system. Using this concept [5–7, 12] expedites an easy description of the rate of particular reactions taking place in the system, taking into consideration such parameters as viscosity of the reaction mixture or size of reagent particles. Taking into account the complexity of linear polymerisation processes, the use of the partial reaction rate constant and associating it with the reaction mixture viscosity changes allows one to define all kinetic parameters in the system and gives an opportunity to group and simplify the systems of balance equations obtained for various polymerisation processes as shown in further sections of this paper [8].

The new take on the expression defining the reaction rate constant, relying on assigning a so-called partial reaction rate constant to every reactant taking part in the reaction, and, in such manner, substituting the reaction rate constant, was proposed for the first time in papers [4–6]. However, those papers used the partial reaction rate constant concept to determine kinetic parameters describing the reaction for obtaining linear polyurethanes, assuming that the constant reaction rate depends on the reagent molecular mass and the polyurethane average molecular mass, whereas paper [7] presents a general form of mass balance equations for particle agglomerations using partial reaction rate constants.

To define a mathematical model describing the heteropolyaddition process polymerisation reaction kinetics (Fig. 1), it was assumed that the polyaddition process is conducted in a tank batch reactor with ideal mixing at constant temperature, and monomers A and B introduced at time t = 0 have the ability to react both amongst each other and the oligomers being produced; however, reactions occur only between different functional groups. Such an assumption gives basis for the conviction that the following reaction types may occur in the reaction mixture:

  • reaction between monomer A and monomer B or oligomers A k B k and A k B k+1 ,

  • reaction between monomer B and monomer A or oligomers A k B k and A k+1B k ,

  • reaction between oligomer A l B l and oligomers A k B k , A k+1 B k and A k B k+1 ,

  • reaction between oligomer A l+1 B l and monomer B or oligomers A k B k and A k B k+1 ,

  • reaction between oligomer A l B l+1 and monomer A or oligomers A k B k and A k+1 B k ,

and so on.

As a result of the presented bulk heteropolyaddition process, a linear structure alternating polymer is produced, i.e., one where monomers A and B alternate resulting in an –ABABABABABA– polymer. Taking into account the partial reaction rate constant concept described by Eq. (1), and taking into consideration the reactions taking place in the reaction mixture during a heteropolyaddition process, the obtained oligomers have been arranged, and partial reaction rate constants as well as chain lengths have been assigned to them (Table 1).

Table 1 Determination of the reaction mixture components and the associated partial reaction rate constants as well as the number of monomers in an oligomer
Full size table

The introduced ordering method allows the simplification, in subsequent parts of the paper, of the mathematical notation describing the polymerisation process, to define the concentration profiles of particular reaction mixture components and to carry out calculations for different reactants’ (monomers A and B) initial concentrations. Such an approach represents a generalisation of research [4, 6], where a uniform initial reactant concentration was assumed, which facilitated an introduction of the concept of the so-called oligomer fractions.

To introduce order, for the purpose of this paper, three oligomer groups were assumed occurring in the reaction mixture:

  • A k B k+1 –“group p”,

  • A k+1 B k –“group n + p”,

  • A k B k –“group 2n + p”.

In such a manner, stoichiometric equations were obtained for the reactions occurring in the analysed heteropolyaddition process:

$$\begin{aligned} & {\text{A}}\;{ + }\;{\text{B}}\mathop \to \limits^{{k_{n + 1} k_{1} }} {\text{AB}} \\ & {\text{A}} + {\text{AB}}\mathop \to \limits^{{k_{n + 1} k_{2n + 1} }} {\text{A}}_{2} {\text{B}} \\ & \ldots \\ & {\text{A}}_{2} {\text{B}} + {\text{A}}_{ 2} {\text{B}}_{2} \mathop \to \limits^{{k_{n + 2} k_{2n + 2} }} {\text{A}}_{ 4} {\text{B}}_{ 3} \\ & {\text{A}}_{ 2} {\text{B}} + {\text{A}}_{ 2} {\text{B}}_{ 3} \mathop \to \limits^{{k_{n + 2} k_{3} }} {\text{A}}_{ 4} {\text{B}}_{4} \\ & \ldots \\ & {\text{B}}\;{ + }\;{\text{AB}}\mathop \to \limits^{{k_{1} k_{2n + 1} }} {\text{AB}}_{2} \\ & {\text{B}} + {\text{A}}_{ 2} {\text{B}}\mathop \to \limits^{{k_{1} k_{n + 2} }} {\text{A}}_{ 2} {\text{B}}_{ 2} \\ & \ldots \\ & {\text{A}}_{ 2} {\text{B}}_{ 3} + {\text{A}}_{ 3} {\text{B}}_{2} \mathop \to \limits^{{k_{3} k_{n + 3} }} {\text{A}}_{ 5} {\text{B}}_{ 5} \\ & {\text{A}}_{ 2} {\text{B}}_{ 3} + {\text{A}}_{ 3} {\text{B}}_{3} \mathop \to \limits^{{k_{3} k_{2n + 3} }} {\text{A}}_{ 5} {\text{B}}_{6} \\ & \ldots \\ & {\text{A}}_{p - 1} {\text{B}}_{p} + {\text{A}}_{p} {\text{B}}_{p} \mathop \to \limits^{{k_{p} k_{2n + p} }} {\text{A}}_{2p - 1} {\text{B}}_{2p} \\ & {\text{A}}_{p} {\text{B}}_{p - 1} + {\text{A}}_{p} {\text{B}}_{p} \mathop \to \limits^{{k_{n + p} k_{2n + p} }} {\text{A}}_{2p} {\text{B}}_{2p - 1} \\ & {\text{A}}_{p} {\text{B}}_{p} + {\text{A}}_{p} {\text{B}}_{p} \mathop \to \limits^{{k_{2n + p} k_{2n + p} }} {\text{A}}_{2p} {\text{B}}_{2p} \\ & \ldots \\ \end{aligned}$$
(3)

where p = 1, 2, …, m.

Using the above stoichiometric equations (3) and applying the designations adopted in Table 1, balance equations have been derived for all reaction mixture components. In the first place, the equation determining the rate for producing component B was determined. This component reacts with monomer A (making A1B1) and all oligomers in the form of A k B k (giving A k B k+1 ) and A k+1 B k (making A k+1 B k+1 ). Thus, we have:

$$\begin{aligned} \frac{{{\text{d}}C_{\text{B}} }}{{{\text{d}}t}} & = \frac{{{\text{d}}C_{1} }}{{{\text{d}}t}} = - k_{1} C_{1} k_{n + 1} C_{n + 1} - k_{1} C_{1} k_{2n + 1} C_{2n + 1} - k_{1} C_{1} k_{n + 2} C_{n + 2} \\ & \quad - k_{1} C_{1} k_{2n + 2} C_{2n + 2} - \cdots - k_{1} C_{1} k_{n + p} C_{n + p} - k_{1} C_{1} k_{2n + p} C_{2n + p} - \cdots \\ \end{aligned}$$
(4)

where p = 1, 2, …, m.

Tidying up the above equations and taking the constant factor of the equation out of the brackets, we get:

$$\frac{{{\text{d}}C_{1} }}{{{\text{d}}t}} = - k_{1} C_{1} \left( {\mathop \sum \limits_{p = 1}^{m} k_{n + p} C_{n + p} + \mathop \sum \limits_{p = 1}^{m} k_{2n + p} C_{2n + p} } \right).$$
(5)

Taking constant factors at every step of the numerical calculations as:

$$S_{\text{A}} = \mathop \sum \limits_{p = 1}^{m} k_{n + p} C_{n + p}$$
(6)
$$S_{\text{AB}} = \mathop \sum \limits_{p = 1}^{m} k_{2n + p} C_{2n + p} ,$$
(7)

expression (5) is transformed into:

$$\frac{{{\text{d}}C_{1} }}{{{\text{d}}t}} = - k_{1} C_{1} (S_{\text{A}} + S_{\text{AB}} ).$$
(8)

Equation (8) describes the rate of monomer B production during heteropolyaddition process, which, in further parts, will be used to create a mass balance system for the heteropolyaddition process.

Proceeding in a similar manner, the rate for producing component A was worked out. Component A reacts with monomer B and all oligomers in the form A k B k (giving A k+1B k ) and A k B k+1 (making A k+1B k+1). Thus, we have:

$$\begin{aligned} \frac{{{\text{d}}C_{\text{A}} }}{{{\text{d}}t}} & = \frac{{{\text{d}}C_{n + 1} }}{{{\text{d}}t}} = - k_{n + 1} C_{n + 1} k_{1} C_{1} - k_{n + 1} C_{n + 1} k_{2n + 1} C_{2n + 1} \\ & \quad - k_{n + 1} C_{n + 1} k_{2} C_{2} - k_{n + 1} C_{n + 1} k_{2n + 2} C_{2n + 2} - \cdots \\ & \quad - k_{n + 1} C_{n + 1} k_{p} C_{p} - k_{n + 1} C_{n + 1} k_{2n + p} C_{2n + p} - \cdots \\ \end{aligned}$$
(9)

where p = 1, 2, …, m.

Taking constant factors k n+1 C n+1 out of the brackets, we get:

$$\frac{{{\text{d}}C_{n + 1} }}{{{\text{d}}t}} = - k_{n + 1} C_{n + 1} \left( {\mathop \sum \limits_{p = 1}^{m} k_{p} C_{p} + \mathop \sum \limits_{p = 1}^{m} k_{2n + p} C_{2n + p} } \right)$$
(10)

In each step of the calculations, the equation factor (10) was substituted with the following expression:

$$S_{\text{B}} = \mathop \sum \limits_{p = 1}^{m} k_{p} C_{p} .$$
(11)

Using Eq. (11), the component A mass balance was described by Eq. (10) in an easy-to-work-with form:

$$\frac{{{\text{d}}C_{n + 1} }}{{{\text{d}}t}} = - k_{n + 1} C_{n + 1} (S_{\text{B}} + S_{\text{AB}} ).$$
(12)

Proceeding analogously as for components A and B of the mixture, the rate for producing subsequent reaction mixture components was determined. In the bulk heteropolyaddition process under analysis, dimer AB reacts with all reaction mixture components. Thus, we have:

$$\begin{aligned} \frac{{dC_{AB} }}{dt} & = \frac{{dC_{2n + 1} }}{dt} = k_{1} C_{1} k_{n + 1} C_{n + 1} - k_{2n + 1} C_{2n + 1} k_{1} C_{1} \\ & \quad - k_{2n + 1} C_{2n + 1} k_{n + 1} C_{n + 1} - k_{2n + 1} C_{2n + 1} k_{2n + 1} C_{2n + 1} - \cdots \\ & \quad - k_{2n + 1} C_{2n + 1} k_{p} C_{p} - k_{2n + 1} C_{2n + 1} k_{n + p} C_{n + p} \\ & \quad - k_{2n + 1} C_{2n + 1} k_{2n + p} C_{2n + p} - \cdots \\ \end{aligned}$$
(13)

where p = 1, 2, …, m.

Using the formulas derived earlier, grouping together and taking out constant equation factors (13) in front of the brackets, we get:

$$\frac{{{\text{d}}C_{2n + 1} }}{{{\text{d}}t}} = k_{1} C_{1} k_{n + 1} C_{n + 1} - k_{2n + 1} C_{2n + 1} (S_{\text{A}} + S_{\text{B}} + S_{\text{AB}} ).$$
(14)

Analogously, equations for subsequent reaction mixture components were derived:

$$\frac{{{\text{d}}C_{2} }}{{{\text{d}}t}} = k_{1} C_{1} k_{2n + 1} C_{2n + 1} - k_{2} C_{2} (S_{\text{A}} + S_{\text{AB}} )$$
(15)
$$\frac{{{\text{d}}C_{n + 2} }}{{{\text{d}}t}} = k_{n + 1} C_{n + 1} k_{2n + 1} C_{2n + 1} - k_{n + 2} C_{n + 2} (S_{\text{B}} + S_{\text{AB}} )$$
(16)
$$\begin{aligned} \frac{{{\text{d}}C_{2n + 2} }}{{{\text{d}}t}} & = k_{n + 1} C_{n + 1} k_{2} C_{2} + k_{1} C_{1} k_{n + 2} C_{n + 2} + k_{2n + 1} C_{2n + 1} k_{2n + 1} C_{2n + 1} \\ & \quad - k_{2n + 2} C_{2n + 2} (S_{\text{A}} + S_{\text{B}} + S_{\text{AB}} ) \cdots \\ \end{aligned}$$
(17)

and so on.

As a result of the analysis of the above Eqs. (14–17), general equations were obtained describing the rate of producing different reaction mixture components for the three groups: “p”, “n + p” and “2n + p” as follows:

$$\frac{{{\text{d}}C_{p} }}{{{\text{d}}t}} = \mathop \sum \limits_{i = 1}^{p - 1} k_{i} C_{i} k_{2n + p - i} C_{2n + p - i} - k_{p} C_{p} (S_{\text{A}} + S_{\text{AB}} )$$
(18)
$$\frac{{{\text{d}}C_{n + p} }}{{{\text{d}}t}} = \mathop \sum \limits_{i = 1}^{p - 1} k_{n + i} C_{n + i} k_{2n + p - i} C_{2n + p - i} - k_{n + p} C_{n + p} (S_{\text{B}} + S_{\text{AB}} )$$
(19)
$$\begin{aligned} \frac{{{\text{d}}C_{2n + p} }}{{{\text{d}}t}} & = \mathop \sum \limits_{i = 1}^{p - 1} k_{i} C_{i} k_{n + p + 1 - i} C_{n + p + 1 - i} + \mathop \sum \limits_{i = 1}^{{{\text{floor}}\left( {\frac{p}{2}} \right)}} k_{2n + i} C_{2n + i} k_{2n + p - i} C_{2n + p - i} \\ & \quad - k_{2n + p} C_{2n + p} (S_{\text{A}} + S_{\text{B}} + S_{\text{AB}} ) \\ \end{aligned}$$
(20)

where floor \(\left( {\frac{p}{2}} \right)\)—a function returning the nearest whole number less than the argument \(\frac{p}{2}\).

The derived equations encompass all possible reagent mass balance equations occurring in the heteropolyaddition process under analysis. Putting together Eqs. (8), (12), (14), (18), (19) and (20), we get the following system of balance equations:

$$\left\{ \begin{aligned} & \frac{{{\text{d}}C_{1} }}{{{\text{d}}t}} = - k_{1} C_{1} (S_{\text{A}} + S_{\text{AB}} ) \\ & \frac{{{\text{d}}C_{n + 1} }}{{{\text{d}}t}} = - k_{n + 1} C_{n + 1} (S_{\text{B}} + S_{\text{AB}} ) \\ & \frac{{{\text{d}}C_{2n + 1} }}{{{\text{d}}t}} = k_{1} C_{1} k_{n + 1} C_{n + 1} - k_{2n + 1} C_{2n + 1} (S_{\text{A}} + S_{\text{B}} + S_{\text{AB}} ) \\ & \frac{{{\text{d}}C_{p} }}{{{\text{d}}t}} = \mathop \sum \limits_{i = 1}^{p - 1} k_{i} C_{i} k_{2n + p - i} C_{2n + p - i} - k_{p} C_{p} (S_{\text{A}} + S_{\text{AB}} ) \\ & \frac{{{\text{d}}C_{n + p} }}{{{\text{d}}t}} = \mathop \sum \limits_{i = 1}^{p - 1} k_{n + i} C_{n + i} k_{2n + p - i} C_{2n + p - i} - k_{n + p} C_{n + p} (S_{\text{B}} + S_{\text{AB}} ) \\ & \frac{{{\text{d}}C_{2n + p} }}{{{\text{d}}t}} = \mathop \sum \limits_{i = 1}^{p - 1} k_{i} C_{i} k_{n + p + 1 - i} C_{n + p + 1 - i} + \mathop \sum \limits_{i = 1}^{{{\text{floor}}\left( {\frac{p}{2}} \right)}} k_{2n + i} C_{2n + i} k_{2n + p - i} C_{2n + p - i} - k_{2n + p} C_{2n + p} (S_{\text{A}} + S_{\text{B}} + S_{\text{AB}} ) \\ \end{aligned} \right.$$
(21)

The mass balance system of Eqs. (21) describes the course of an alternating linear polymer heteropolyaddition process in a batch reactor with ideal mixing operating in isothermal conditions. The system mass balance (21) describes the chain growth stage in the step polymerisation process, assuming that the polymerisation process does not end and that chain transfer process occurs. The homopolyaddition process analysis was carried out based on the assumption that all monomers in the reaction mixture are able to react in the polymerisation process. Based on the balance equations system (21), a calculation algorithm was set up in Mathcad 15.0 Professional, facilitating an approximation of the process kinetic parameters and, consequently, determination of the linear polymer heteropolyaddition reaction rate.

A review of the international literature shows [4] that the most common approach for solving kinetic issues in linear polymer synthesis processes is the generally known Flory’s method, assuming a uniform value for the reaction rate constant across the entire polymerisation process. As is evident from the literature data [1], reaction mixture viscosity during the course of a polymerisation process in very many cases is not constant, but changes together with the change in the average molar mass of the produced polymer. Changes in the reaction mixture viscosity most often manifest themselves by an increase in its numeric value. That is why in the cases where the increase in viscosity is significant, it seems necessary to take this into account in the polymerisation process kinetic analysis.

Reaction mixtures in polymerisation processes are characterised by various types of interactions, which influence polymer properties. The occurrence of macro-molecule chain entanglements causes linear polymer viscosity both in the state of a solution and in the melt state to increase acutely [9]. The scope of the linear viscosity increase in the number-average molecular mass function is described by the following equation:

$$\eta = {\text{const }}M_{\text{n}} .$$
(22)

Then, after reaching a certain critical polymer length, the slope of the solution viscosity curve gets smaller as described by the relation [10]:

$$\eta = {\text{const }}M_{\text{n}}^{3,4} .$$
(23)

As shown in the above discussion, polymerisation system viscosity changes during the course of polymerisation. Undoubtedly, the change in viscosity in polymer solutions is associated with the change in the hydrodynamic interaction between the generated macro-particles as well as between the macro-particles and solvent. Due to the constant growth of polymer chains during living polymerisation, hydrodynamic interactions in the reaction solution are also subject to constant change causing an increase in viscosity. Hydrodynamic interactions during liquid laminar flow through a horizontal tube are described by the following equation:

$$Q = \frac{{\pi R_{p}^{4} }}{8\eta }\frac{\Delta p}{l}.$$
(24)

Equation (24) describing a laminar flow of incompressible liquid in stationary state in a cylindrical conduit shows that the volumetric flow rate Q is inversely proportional to liquid viscosity η. In this paper, it has been assumed, similar to the Hagen–Poiseuille’s law, that the reaction rate r is inversely proportional to the reaction mixture dynamic viscosity η in laminar flow. Whereas in accordance with the presented relation (22), an increase in reaction mixture viscosity is directly proportional to the number-average molecular mass of the produced polymer. Such an assumption stems from an increase in hydrodynamic interactions in the reaction solution caused by the increase in polymer number-average molecular mass. Taking into account the impact of the increase in viscosity on the polymerisation process rate, a correction coefficient Z i was introduced allowing the expression of the partial reaction rate constant k i as follows:

$$k_{i} = k_{1} \cdot Z_{i} (M_{\text{n}} ).$$
(25)

The correction coefficient Z i introduced in Eq. (25) is a function of the reaction mixture number-average molecular mass. To define the Z i (M n) function, one of the simplest possible forms of the correction coefficient Z i was used stemming from flow resistance in laminar flow, i.e.,:

$$Z_{i} (M_{\text{n}} ) = \gamma \cdot (M_{\text{n}} /M_{0} )^{ - p}$$
(26)

Equation (26) defines a correction coefficient, which is a dimensionless quantity, where two characteristic parameters γ and p occur for a given polymerisation process. Thus, the partial reaction rate constant k i decreases with the increase of the number-average molar mass of the produced polymer.

Consequently, through the introduction of the Z i correction coefficient, a significant simplification of the system (21) describing the heteropolyaddition p was achieved as well as an opportunity to associate kinetic parameters k i with the number-average molar mass of M n system. Taking into account the relationship (25) and the relationship between the correction coefficient with the number-average molar mass M n of the generated polymer (26), a relation was obtained linking the viscosity changes to the partial reaction rate constant k i , as depicted by the following expression:

$$k_{j} = k_{1} \cdot \gamma \cdot (M_{\text{n}} /M_{0} )^{ - p}$$
(27)

Taking into account Eq. (27) and Eqs. (22) and (23), describing reaction system viscosity changes as a function of the number-average molar mass, an explicit relation between reaction mixture viscosity change and polymerisation process kinetic parameters was obtained as follows:

$$\eta = {\text{const}} \cdot M_{0} \left( {\frac{{k_{1} \cdot \gamma }}{{k_{i} }}} \right)^{{\frac{1}{p}}}$$
(28)

By introducing a new constant λ defined as:

$$\lambda = \gamma \cdot ({\text{const}} \cdot M_{0} )^{p} \;,$$
(29)

the above equation was transformed into:

$$k_{i} = k_{1} \cdot \lambda \cdot \eta^{ - p}$$
(30)

Equation (30) shows that an increase in the reaction system viscosity causes a decrease in the partial reaction rate constant value as the reaction progresses.

Obtained results

Calculations associated with the heteropolyaddition process kinetics were carried out using a system of equations (21), taking into account, at every step of the calculations, the impact of viscosity change stemming from the increase in the number-average molar mass of the produced polymer. The calculations were carried out, assuming constant kinetic parameter values during the course of the process k = const as well as the assumption that they change due to a change in system viscosity during the course of the reaction. Having the test results describing the relation between number-average molar mass M n and the time in the diphenyl carbonate and bisphenol A diglycidyl ether heteropolyaddition process and the data describing the initial concentrations of diphenyl carbonate [A]0 and diglycidyl ether of bisphenol A [B]0 monomers, including the performance times of the polymerisation process at 100 °C, the molar masses of diphenyl carbonate M A and diglycidyl ether of bisphenol A M B monomers, numerical integration was performed with the use of balance equations (21). Numeric integration was based on the Euler’s iteration method [11].

The kinetic parameters k i estimation was carried out on the basis of experimental research results, using the simplex optimisation method. In the simplex optimisation method, the value of function S, defined by the sum of squares of differences of the calculated values O i and experimental values E i , was minimised. The optimal numerical value for this constant was determined by minimising the numerical value of the objective function defined by the following equation:

$$S = \mathop \sum \limits_{i = 1}^{b} \left( {O_{i} - E_{i} } \right)^{2} \to { \hbox{min} } .$$
(31)

The estimated kinetic parameters facilitated a determination of all process kinetic parameters and, thus, the changes in the number-average molar mass M n [g/mol] over time (Fig. 2) and the molar mass effects of particular reaction mixture components in time. The consequence of the proposed model (21) was the possibility to determine all process kinetic parameters k i through the estimation of only two parameters p and γ occurring in Eqs. (29, 30). Therefore, introduction of the partial reaction rate constant concept and associating that quantity with the changes in reaction mixture viscosity boiled down the issue of determining kinetic parameters for heteropolyaddition process to the estimation of three parameters k 1, p and γ. The p and γ parameters of Eqs. (29, 30) have been determined using experimental research [1]. The p and γ parameters determined in such a manner have allowed the calculation of approximate partial reaction rate constant (Table 2) and to plot the relationship between number-average molar mass M n and time (Fig. 2) and the relationship between the monomer conversion degree α and time (Fig. 3).

Fig. 2
figure 2

Number-average molar mass M n [g/mol] relations of time in the heteropolyaddition process in the mass of diphenyl carbonate (1 mmol) and bisphenol A diglycidyl ether (1 mmol) with the use of tetrabutylphosphonium chloride (TBPC) catalyst at temperature t 1 = 100 °C—calculations using model (21) with k i  = const;—calculations using model (21) with k i = k 1 Z i; blue square experimental data [1] (colour figure online)

Full size image
Table 2 Selected partial reaction rate constant k i [(dm3/(mol s))½] values in the heteropolyaddition process in the mass of diphenyl carbonate (1 mmol) and bisphenol A diglycidyl ether (1 mmol) with the use of tetrabutylphosphonium chloride (TBPC) catalyst at temperature t 1 = 100 °C calculated using model (21)
Full size table
Fig. 3
figure 3

Monomer conversion rate α [%] relationship over time in the heteropolyaddition process in the mass of diphenyl carbonate (1 mmol) and bisphenol A diglycidyl ether (1 mmol) with the use of tetrabutylphosphonium chloride (TBPC) catalyst at temperature t 1 = 100 °C—calculations using model (21) with k i  = k 1 Z i ; blue square experimental data [1] (colour figure online)

Full size image

The points in Figs. 2 and 3 represent the relationship obtained from the literature [1], i.e., the straight line in Fig. 2 is plotted based on the assumption on constant kinetic parameter values, whereas the curve (red) represents the relationship calculated using model (21) with a constant reaction rate dependent on the average polymer molecular mass k i  = k 1 Z i .

In the event of adopting a uniform constant reaction rate value in the heteropolyaddition process, a value of the objective function (31) equal to S min = 18.63 × 107 g/mol was obtained, whereas taking into account viscosity changes through varying partial reaction rate constant in accordance with Eq. (30) gives a function value equal to S min = 2.74 × 107 g/mol. The obtained results unanimously point to the influence of the reaction medium viscosity on the change to heteropolyaddition process rate, which should be accounted for in the calculations.

A comparison of number-average molar mass experimental values M n [g/mol] with theoretical values calculated assuming a uniform reaction rate constant value and values calculated assuming a constant rate dependent on viscosity changes in the heteropolyaddition process in the mass of diphenyl carbonate and bisphenol A diglycidyl ether is presented in Table 3.

Table 3 A comparison of number-average molar mass experimental values M n [g/mol] with the literature values calculated assuming a uniform reaction rate constant value and values calculated assuming a constant rate dependent on viscosity changes in the heteropolyaddition process in the mass of diphenyl carbonate and bisphenol A diglycidyl ether (1 mmol) with the use of tetrabutylphosphonium chloride (TBPC) catalyst in temperature t 1 = 100 °C
Full size table

Using the results of Table 3, an additional correlation coefficient β(η) was introduced, taking into account the effect of viscosity on the polymerisation process, which is expressed by the following equation:

$$\beta (\eta ) = \frac{{S_{C} - S_{\eta } }}{{S_{C} }}.$$
(32)

In the above expression, the following symbols are used: S c —results of calculations not taking into account viscosity changes, S η —results of calculations taking into account viscosity changes, β(η)—numeric value of the correlation coefficient is within the (0,1) range: β(η) \(\in\) (0, 1).

Using expression (32) and the results tabulated in Table 3, the correlation coefficient β(η) has been calculated:

$$\beta (\eta ) = \frac{{18.63 \times 10^{7} - 2.74 \times 10^{7} }}{{18.63 \times 10^{7} }} = 0.853.$$
(33)

The estimated diphenyl carbonate and bisphenol A diglycidyl ether heteropolyaddition process kinetic parameters allowed the determination of the values of the correction coefficient Z i (Fig. 4) and, then, the partial reaction rate constant; thus, they have allowed the determination, with the use of Eqs. (29, 30), of the reaction rate constants at every step of the numeric calculations. The determined kinetic parameters as a function of time are depicted in Fig. 5.

Fig. 4
figure 4

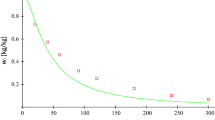
Correction coefficient Z i change as a function of an average molar mass M sr [g/mol] of the produced polycarbonate in temperature of 100 °C calculated using model (21)

Full size image
Fig. 5
figure 5

Relation between partial reaction rate constant k i [(dm3/(mol·s))½] and time in the heteropolyaddition process in the mass of diphenyl carbonate (1 mmol) and bisphenol A diglycidyl ether of (1 mmol) with the use of tetrabutylphosphonium chloride (TBPC) catalyst at temperature t 1 = 100 °C calculated using model (21)

Full size image

The determined correction coefficient values presented in Fig. 5 indicated a significant effect of the increase in the average molar mass on increasing viscosity in the initial phase of the polymerisation process, which translates into a significant decrease in the partial reaction rate constant (Fig. 5) in this phase of the polymerisation process. In the final phase, when the polymer average molar mass growth dynamics decreases, the changes in partial reaction rate constants also decrease.

The estimated kinetic parameters presented in Table 2 allowed to determine the concentrations of particular components of the reaction mixture during the heteropolyaddition process in the mass of diphenyl carbonate and bisphenol A diglycidyl ether with the use of tetrabutylphosphonium chloride (TBPC) catalyst at temperature t 1 = 100 °C.

The conducted calculations clearly show that there is a significantly better match with experimental data if the reaction mixture viscosity changes stemming from the increase in the polymer average molecular mass are taken into account, which points to the necessity of including these changes in polymerisation process rate calculations, particularly in the cases where significant system viscosity changes take place.

It should be emphasised that the proposed method for determining kinetic parameters mostly pertains to the cases where reaction solution viscosity significantly influences the rate of the polymerisation process. The measure of such an influence of viscosity on polyaddition process rate is the correction coefficient Z i , related with average molar mass of the produced polymer. It should be pointed out that the correction coefficient Z i in the analysed 1,4-benzenedicarbonyl chloride with bisphenol A diglycidyl ether changed within the range of 1.6–0.2 (Fig. 4), which indicates a significant impact of viscosity changes in the course of that process.

Conclusions

The subject of the analysis was mass balance conducted on the experimental literature data obtained for the polyaddition process in the mass of diphenyl carbonate and bisphenol A diglycidyl ether in a batch reactor with ideal mixing at temperature t 1 = 100 °C, in time of 48 h [1]. As the number of mass balance equations is equal to the number of independent reactions during the process, and to carry out a numerical analysis of the system of these equations, the knowledge of reaction rate constants is required, since we are dealing here with a very complex numerical task. This paper suggests a simplification of this concept by introducing a partial reaction rate constant defined by Eq. (1), the application of which facilitates a reduction in the number of mass balance equations to the number of regulating components in the system and allows us to relate process kinetic parameters to the average molecular mass of the produced polymer and, as a consequence, the viscosity of the reaction mixture.

Based on both the literature data and the conducted analysis, kinetic parameters of the analysed process have been determined, and the effect of the reaction medium viscosity changes on the rate of polymerisation has been calculated, which allowed the determination of the degree to which experimental values available in the literature [12] are matched by the values calculated using the proposed model. The results of the conducted analysis are shown in Table 4. The data presented in Table 4 show that when it comes to the process under analysis, it is significant to take into account the viscosity changes in the polymerisation process and, thus, to determine the process kinetic parameters, which change as a result of the said viscosity changes. The measure of the impact of viscosity on the polymerisation process is, in this case, the value of correlation coefficient β, the value of which increases together with the increase of the impact of viscosity in the course of the process.

Table 4 Objective function values and correlation coefficient determined for the cases under consideration in this paper
Full size table

The application of the presented method to solve a system of mass balance equations indicates a flexibility of the proposed method as it provides an opportunity to estimate all kinetic parameters if:

  • the reaction rate is not dependent on viscosity increase, the Flory’s method is satisfied and then parameter p in expression (29) is equal to zero, p = 0, and parameter γ = 1,

  • the reaction rate is dependent on viscosity increase and on average molecular mass, and then parameter p in expression (29) is not equal to zero, p ≠ 0, and parameter γ > 0.

The mathematical model proposed by the authors provides an opportunity to estimate all kinetic parameters for the analysed process. A very important aspect of the proposed method, speaking for its flexibility, is the possibility of associating kinetic parameters not only with the reaction system viscosity changes, which requires these changes to be taken into account at every step of the numerical calculations, but also with other quantities potentially affecting the rate of polymerisation process, e.g., the size of macromolecules. Accounting for other parameters affecting partial reaction rate constants is easily done by an additional introduction into the correction coefficient Z i , a factor functionally connected with, for example, the macro-particle molar mass. In such a case, expression (25) would be as follows:

$$k_{i} = k_{1} \cdot Z_{i} (M_{\text{n}} ,M_{i} ).$$