Gene expression noise is affected differentially by feedback in burst frequency and burst size

Abstract

Inside individual cells, expression of genes is stochastic across organisms ranging from bacterial to human cells. A ubiquitous feature of stochastic expression is burst-like synthesis of gene products, which drives considerable intercellular variability in protein levels across an isogenic cell population. One common mechanism by which cells control such stochasticity is negative feedback regulation, where a protein inhibits its own synthesis. For a single gene that is expressed in bursts, negative feedback can affect the burst frequency or the burst size. In order to compare these feedback types, we study a piecewise deterministic model for gene expression of a self-regulating gene. Mathematically tractable steady-state protein distributions are derived and used to compare the noise suppression abilities of the two feedbacks. Results show that in the low noise regime, both feedbacks are similar in term of their noise buffering abilities. Intriguingly, feedback in burst size outperforms the feedback in burst frequency in the high noise regime. Finally, we discuss various regulatory strategies by which cells implement feedback to control burst sizes of expressed proteins at the level of single cells.

Appendices

Appendix A: Reduction to the deterministic limit

In the main text we showed that, irrespective of whether the feedback acts on the burst frequency or burst size, the steady-state mean $\langle x\rangle$ of the protein concentration tends in the small-noise limit $\varepsilon \rightarrow 0$ to the fixed point $x_\mathrm{s}$ of the ordinary differential equation (14). Here we provide a stronger result, showing that for both feedback types the master equation (3)–(4) reduces as $\varepsilon \rightarrow 0$ to Liouville’s partial differential equation associated with the ordinary differential equation (14). Thus, we show that both regulation strategies yield the same deterministic model in the limit of small noise.

For feedback in burst frequency (8) the probability flux (4) is given by

$$\begin{aligned} J = - x p(x,t) + \frac{1}{\varepsilon }\int _0^x \frac{\mathrm{e}^{-\frac{x-y}{\varepsilon }} p(y,t) \mathrm{d}y}{1 + (y/K)^H} \end{aligned}$$

(A.1)

If $\varepsilon$ is small, a dominant contribution to the integral in (A.1) comes from a neighbourhood of the upper integration limit $y=x$. Following Watson’s lemma (Hinch 1991), we extend the lower integration limit in (A.1) to $-\infty$ and use the approximation

$$\begin{aligned} \frac{p(y,t)}{1 + (y/K)^H} \sim \frac{p(x,t)}{1 + (x/K)^H} \quad \text {for } y \text { that is close to } x, \end{aligned}$$

(A.2)

obtaining

$$\begin{aligned} J \sim - x p + \frac{p}{1 + (x/K)^H} \end{aligned}$$

(A.3)

at the leading order; higher-order terms, which are not required for our present purposes, can be determined by including in (A.2) additional terms of the Taylor series expansion in y around x. The right-hand side of (A.3), being the product of the protein pdf and the right-hand side of the ODE (14), gives the flux of probability induced by the drift of the deterministic model. Inserting (A.3) into the probability conservation law (3) yields a Liouville equation (Schuss 2009, p. 213)—a Chapman–Kolmogorov equation without diffusion or jumps—whose solutions are time-dependent pdfs for a variable which evolves deterministically according to (14). Thus, the stochastic model with feedback in burst frequency given by the conservation law (3) and (A.1) reduces as $\varepsilon$ tends to zero to the deterministic model (14).

If feedback acts on burst size (19), the probability flux (4) simplifies to

$$\begin{aligned} J = - x p(x,t) + \frac{1}{\varepsilon }\int _0^x \mathrm{e}^{-\frac{1}{\varepsilon }\int _y^x 1 + (z/K)^H\mathrm{d}z} p(y,t)\mathrm{d}y. \end{aligned}$$

(A.4)

Again, a neighbourhood of the upper limit $y=x$ of integration dominates in its contribution to the integral in (A.4). Therefore, we extend the lower integration limit to $-\infty$ without incurring appreciable error; we also use the approximations

$$\begin{aligned} \int _y^x 1 + (z/K)^H \mathrm{d}z \sim (1 + (x/K)^H)(x-y),\quad p(y,t) \sim p(x,t), \end{aligned}$$

(A.5)

which are valid for y that is close to x. Inserting (A.5) into (A.4) and integrating the simple exponential, we obtain the same leading-order approximation (A.3) for the probability flux (A.4) as we previously did for the flux (A.1). Thus, whether the bursting stochastic model operates a feedback in burst frequency (A.1) or in burst size (A.4), it reduces to the same deterministic model (14) in the small-noise limit of $\varepsilon \rightarrow 0$.

Appendix B: Strong feedback asymptotics (burst size)

Inserting the second Lyapunov function (20) into the WKB form (9), we obtain

$$\begin{aligned} p(x) = C x^{\frac{1}{\varepsilon }-1} \mathrm{e}^{-\frac{1}{\varepsilon }\left( \frac{x^{H+1}}{(H+1)K^H} + x\right) } \end{aligned}$$

(B.1)

for the protein pdf in the case of feedback in burst size.

Similarly as in the Main Text, we express the protein moments as

$$\begin{aligned} \langle x^n \rangle = \frac{B_n}{B_0}, \end{aligned}$$

(B.2)

where instead of (26) we have

$$\begin{aligned} B_n = \int _0^\infty x^{\frac{1}{\varepsilon } - 1 + n} \mathrm{e}^{-\frac{1}{\varepsilon }\left( \frac{x^{H+1}}{(H+1)K^H} + x\right) } \mathrm{d}x. \end{aligned}$$

(B.3)

Again, $B_0^{-1}=C$ is the normalisation constant. Substituting $x=Ky$ in the integral (B.3) yields

$$\begin{aligned} B_n = K^{\frac{1}{\varepsilon }+n} A_n, \end{aligned}$$

(B.4)

where

$$\begin{aligned} A_n = \int _0^\infty y^{\frac{1}{\varepsilon } - 1 + n} \mathrm{e}^{-\lambda \left( \frac{y^{H+1}}{H+1} + y \right) } \mathrm{d}y, \end{aligned}$$

(B.5)

in which $\lambda =K/\varepsilon$ is an auxiliary parameter.

In the case of strong feedback, we have $\lambda \ll 1$, which implies $y\gg 1$, and therefore the term $y^{H+1}/(H+1)$ dominates the term y in the exponential of (B.5), so that

$$\begin{aligned} A_n \sim \int _0^\infty y^{\frac{1}{\varepsilon } - 1 + n} \mathrm{e}^{-\frac{\lambda y^{H+1}}{H+1}} \mathrm{d}y = \frac{1}{\lambda }\left( \frac{H+1}{\lambda }\right) ^{\frac{\varepsilon ^{-1} + n}{1+H} - 1} {\varGamma }\left( \frac{\varepsilon ^{-1} + n}{1+H}\right) , \end{aligned}$$

(B.6)

where ${\varGamma }(z)$ is the gamma function (Abramowitz and Stegun 1972). Unlike for feedback in burst frequency, here is no need to treat $A_0$ differently from $A_1$ or $A_2$.

For the protein mean we have

$$\begin{aligned} \langle x \rangle = \frac{B_1}{B_0} = \frac{K A_1}{A_0} \sim D_\varepsilon K^{\frac{H}{H+1}}, \end{aligned}$$

(B.7)

where the prefactor $D_\varepsilon$ is given by

$$\begin{aligned} D_\varepsilon = (\varepsilon (H+1))^{\frac{1}{H+1}}\frac{{\varGamma }\left( \frac{\varepsilon ^{-1} + 1}{H + 1}\right) }{{\varGamma }\left( \frac{\varepsilon ^{-1}}{H + 1}\right) }. \end{aligned}$$

(B.8)

Unlike for feedback in burst frequency, which yielded a slow logarithmic decrease of the mean with decreasing dissociation constant K, here we obtain a faster power-law decrease, which is consistent with the LNA prediction (44). Additionally, as $\varepsilon$ tends to zero the prefactor $D_\varepsilon$ converges to one, which is the prefactor of the LNA-predicted power law. The asymptotics of $D_\varepsilon$ as $\varepsilon \rightarrow 0$ follow from

$$\begin{aligned} \frac{{\varGamma }(z + a)}{{\varGamma }(z)} \sim z^a,\quad z\gg 1, \end{aligned}$$

(B.9)

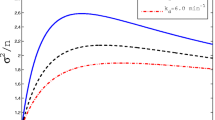
in which we take $z=\varepsilon ^{-1}/(H+1)$ and $a=1/(H+1)$; see Abramowitz and Stegun (1972) for this and other properties of the gamma function. These results suggest that, unlike for feedback in burst frequency, where the LNA approximation could only be used for intermediate ranges of K, here the LNA yields a uniform (i.e. valid for all K) approximation (Fig. 7).

For the protein CV$^2$ we have

$$\begin{aligned} \mathrm{CV}^2 = \frac{B_2 B_0}{B_1^2} - 1 = \frac{A_2 A_0}{A_1^2} - 1 \sim \frac{{\varGamma }\left( \frac{\varepsilon ^{-1}}{H+1} \right) {\varGamma }\left( \frac{\varepsilon ^{-1}+2}{H+1}\right) }{{\varGamma }^2 \left( \frac{\varepsilon ^{-1}+1}{H+1}\right) } - 1, \end{aligned}$$

(B.10)

which, for a fixed $\varepsilon$, is a constant independent of K. As $\varepsilon$ tends to zero, we can again use (B.9) to show that the right-hand side of (B.10) is equal to $\varepsilon /(H+1)$ at the leading order in $\varepsilon$, which is the same value as that obtained by taking K very small in the LNA prediction (23). This suggests that the LNA approximation of the coefficient of variation, like that of the mean, can be used uniformly for all K.

Appendix C: Noncooperative feedback

Here we present variants of the figures from the Results in the Main Text obtained by taking $H=1$ (noncooperative feedback) instead of $H=4$. We shall not repeat the points made in the Main Text, focusing instead on the main differences that occur in the absence of cooperativity.

Fig. 7

Protein distributions for varied feedback strength. $\varepsilon =0.2$

Fig. 8

Protein mean and CV$^2$ in response to strengthening feedback in burst frequency

$\mathbf{CV}^2$ monotonically increases with strengthening noncooperative feedback in burst frequency In contrast with the cooperative case, where a gradual increase in burst-frequency feedback strength led at first to a transient decrease in protein noise (Fig. 3), without cooperativity the CV$^2$ is strictly increasing (Fig. 8).

Protein mean and $\mathbf{CV}^2$ are less sensitive to feedback strength Wider ranges of dissociation constants are required to achieve similar changes in protein mean and noise as those reported previously. In order to appreciate this, one needs to compare the scales on the horizontal axes of Figs. 8, 9, 10, 11 with those of their counterparts in the Main Text.

Noncooperative performs worse than the cooperative in reducing noise Noncooperative feedback, even if acting through burst size, leads at best to a $50~\%$ reduction in CV$^2$ (Fig. 11), which is inferior to a $80~\%$ reduction achievable in the cooperative case with $H=4$ (Fig. 6).

The main conclusion of the Main Text holds also in noncooperative case. The regulation in burst size performs better in reducing noise, especially for noisy proteins subject to strong self-repression (Fig. 11).

Fig. 9

Impact of strengthening feedback in burst frequency on mean and CV$^2$ of a noisy protein ($\varepsilon =0.5$). Comparison of exact results (full line) with LNA (dashed line) and small K (dotted line) asymptotics

Fig. 10

Protein mean and CV$^2$ in response to strengthening feedback in burst size

Fig. 11

Relative squared coefficient of variation ($\mathrm{CV}^2_\mathrm{rel}$), i.e. the ratio of the regulated protein CV$^2$ relative to that of a constitutive protein for feedback in burst frequency and size

Appendix D: Discrete simulations

The discrete model is a chemical system of two species (Wilkinson 2006), A and P, whereby $A\in \{0,1\}$ is an indicator variable describing whether the gene is active ($A=1$) or inactive ($A=0$) and P gives the number of protein.

Table 1 Reactions, their stoichiometries, and rates for the discrete stochastic model

The two species are subject to four reactions, gene activation, gene inactivation, protein production, and protein decay. Each reaction is characterised by the change in copy numbers that a single occurrence of the reaction induces and by the stochastic rate with which the reaction occurs (Table 1).

The dependence of the rates of activation $\tilde{k}_\mathrm{on}(P)$, inactivation $\tilde{k}_\mathrm{off}(P)$, protein production $\tilde{k}_\mathrm{p}(P)$ and protein decay $\tilde{k}_\mathrm{d}(P)$ is as yet undefined in Table 1, but is specified below for feedbacks in burst frequency and burst size. We use tildes to distinguish the microscopic rates (expressed in terms of individual molecules) from the macroscopic ones (expressed in terms of concentrations) which were used throughout the Main Text.

For feedback in burst frequency, we choose

$$\begin{aligned} \tilde{k}_\mathrm{on}(P)= \frac{\varepsilon ^{-1}}{1 + (P/K{\varOmega })^H},\quad \tilde{k}_\mathrm{p}(P) = \frac{\varepsilon {\varOmega }}{\delta },\quad \tilde{k}_\mathrm{off}(P) = \frac{1}{\delta },\quad \tilde{k}_\mathrm{d}(P) = P, \end{aligned}$$

(D.1)

while for feedback in burst size, we use

$$\begin{aligned} \tilde{k}_\mathrm{on}(P)= \varepsilon ^{-1},\quad \tilde{k}_\mathrm{p}(P) = \frac{\varepsilon {\varOmega }}{\delta (1 + (P/K{\varOmega })^H)},\quad \tilde{k}_\mathrm{off}(P) = \frac{1}{\delta },\quad \tilde{k}_\mathrm{d}(P) = P. \end{aligned}$$

(D.2)

In addition to the noise parameter $\varepsilon$, dimensionless dissociation constant K and the cooperativity coefficient H, which have been introduced in the Main Text, cf. Eq. (8) and (19), we have in (D.1) and (D.2) two new parameters: $\delta$ and ${\varOmega }$. The parameter $\delta$ compares the time scale of gene activity to that of protein turnover, and ${\varOmega }$ is the system size parameter: the number of proteins corresponding to the unit of concentration.

Provided that $\delta \ll 1$ and ${\varOmega }\gg 1$, the protein concentration defined as $x=P/{\varOmega }$ can be compared to the predictions of the continuous bursting model (7). For mathematical analysis of the bursting asymptotics ($\delta \ll 1$) as well as system-size asymptotics (${\varOmega }\gg 1$), we refer the reader to Bokes et al. (2012).

In Fig. 2, we used $\varepsilon =0.2$, $H=4$, a range of values of K (detailed within the figure panels), $\delta =0.01$ and ${\varOmega }=100$. Each distribution was estimated from a single large run ($10^5$ iterations) of Gillespie’s direct method (Gillespie 1977) implemented in the StochPy stochastic modelling software package (Maarleveld et al. 2013).