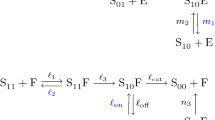Global stability of a class of futile cycles

Abstract

In this paper, we prove the global asymptotic stability of a class of mass action futile cycle networks which includes a model of processive multisite phosphorylation networks. The proof consists of two parts. In the first part, we prove that there is a unique equilibrium in every positive compatibility class. In the second part, we make use of a piecewise linear in rates Lyapunov function in order to prove the global asymptotic stability of the unique equilibrium corresponding to a given initial concentration vector. The main novelty of the paper is the use of a simple algebraic approach based on the intermediate value property of continuous functions in order to prove the uniqueness of equilibrium in every positive compatibility class.

1 Introduction

We consider the following class of futile cycles:

$$\begin{aligned} \begin{array}{ccccccccccc} P_0+E_1 &{} \overset{k_{11}}{\underset{k_{-11}}{\rightleftharpoons }} &{} C_{11} &{} \overset{k_{12}}{\underset{k_{-12}}{\rightleftharpoons }} &{} C_{12} &{} \overset{k_{13}}{\underset{k_{-13}}{\rightleftharpoons }} &{} \cdots \cdots &{} \overset{k_{1m_1}}{\underset{k_{-1m_1}}{\rightleftharpoons }} &{} C_{1m_1} &{} \overset{k_{1(m_1+1)}}{\longrightarrow } &{} P_1+E_1 \\ P_1+E_2 &{} \overset{k_{21}}{\underset{k_{-21}}{\rightleftharpoons }} &{} C_{21} &{} \overset{k_{22}}{\underset{k_{-22}}{\rightleftharpoons }} &{} C_{22} &{} \overset{k_{23}}{\underset{k_{-23}}{\rightleftharpoons }} &{} \cdots \cdots &{} \overset{k_{2m_2}}{\underset{k_{-2m_2}}{\rightleftharpoons }} &{} C_{2m_2} &{} \overset{k_{2(m_2+1)}}{\longrightarrow } &{} P_2+E_2 \\ &{} &{} \vdots &{} &{} &{} \vdots &{} &{} &{} \vdots &{} &{} \\ P_{n-1}+E_n &{} \overset{k_{n1}}{\underset{k_{-n1}}{\rightleftharpoons }} &{} C_{n1} &{} \overset{k_{n2}}{\underset{k_{-n2}}{\rightleftharpoons }} &{} C_{n2} &{} \overset{k_{n3}}{\underset{k_{-n3}}{\rightleftharpoons }} &{} \cdots \cdots &{} \overset{k_{nm_n}}{\underset{k_{-nm_n}}{\rightleftharpoons }} &{} C_{nm_n} &{} \overset{k_{n(m_n+1)}}{\longrightarrow } &{} P_0+E_n \end{array} \end{aligned}$$

(1)

We give a few words of explanation regarding the above class of futile cycles. There are n reaction chains shown in (1). It is assumed that the $k{\text {{th}}}$ reaction chain has the first $m_k$ reactions reversible and the last reaction irreversible as shown in (1). For the $i{\text {{th}}}$ reaction chain ($i=1,\ldots ,n$), $C_{ij}$ $(j=1,\ldots ,m_i)$ denote the intermediate complexes and $E_i$ denotes the enzyme catalyzing the generation of the product $P_i$ from the substrate $P_{i-1}$, assuming that $P_n$ and $P_0$ denote the same compound. It is assumed that each of the reactions in (1) is governed by mass action kinetics. Thus each reaction chain in (1) is a reaction mechanism of an enzyme catalyzed single substrate, single product reaction. Since the product of the last reaction chain is the substrate of the first one, (1) is a futile cycle. For $i=1,\ldots ,n$, $j=1,\ldots ,m_i+1$, $k_{ij}$ denotes the forward reaction constant and for $i=1,\ldots ,n$, $j=1,\ldots ,m_i$, $k_{-ij}$ denotes the reverse reaction constant of the $j{{\text {th}}}$ reaction in the $i{\text {{th}}}$ reaction chain.

One example of a futile cycle model in biochemistry of the type (1) is the model of processive multisite phosphorylation system discussed in Conradi and Shiu (2015). Phosphorylation systems play a vital role in cellular signalling, and their stability properties are of great interest. For a detailed exposition on phosphorylation systems, the reader is referred to Salazar and Høfer (2009). There are two primary mechanisms and related mathematical models of multisite phosphorylation systems. These are distributive and processive mechanisms. The processive mechanism of multisite phosphorylation system discussed in Conradi and Shiu (2015) looks as follows:

$$\begin{aligned} \begin{array}{ccccccccccc} P_0+E_1 &{} \overset{k_{11}}{\underset{k_{-11}}{\rightleftharpoons }} &{} C_{11} &{} \overset{k_{12}}{\underset{k_{-12}}{\rightleftharpoons }} &{} C_{12} &{} \overset{k_{13}}{\underset{k_{-13}}{\rightleftharpoons }} &{} \cdots \cdots &{} \overset{k_{1m}}{\underset{k_{-1m}}{\rightleftharpoons }} &{} C_{1m} &{} \overset{k_{1(m+1)}}{\longrightarrow } &{} P_1+E_1 \\ P_1+E_2 &{} \overset{k_{21}}{\underset{k_{-21}}{\rightleftharpoons }} &{} C_{21} &{} \overset{k_{22}}{\underset{k_{-22}}{\rightleftharpoons }} &{} C_{22} &{} \overset{k_{23}}{\underset{k_{-23}}{\rightleftharpoons }} &{} \cdots \cdots &{} \overset{k_{2m}}{\underset{k_{-2m}}{\rightleftharpoons }} &{} C_{2m} &{} \overset{k_{2(m+1)}}{\longrightarrow } &{} P_0+E_2 \end{array} \end{aligned}$$

(2)

Note that this mechanism is a specific case of the kind of futile cycles (1) under consideration in this paper.

It has been shown (Wang and Sontag 2008) that a distributive multisite phoshorylation mechanism can exhibit the property of multistationarity if there are at least two sites of phosphorylation, meaning that there can be more than one equilibrium in every positive compatibility class. However, it has been shown (Conradi and Shiu 2015) that a processive multisite phosphorylation system admits a unique equilibrium in every positive compatibility class. We explain in simple words what this means. Any chemical reaction network has a set of conservation laws. For example, it can be shown that the futile cycle (1) under consideration in this paper has the sum of the concentrations of all the substrates $P_i$ $(i=0,\ldots ,n-1)$ and the intermediate complexes $C_{ij}$ conserved and positive. Also it can be easily proven that for the $i{\text {{th}}}$ reaction chain, the sum of the concentrations of the enzyme $E_i$ and all the intermediate complexes $C_{ij}$ $(j=1,\ldots ,m_i)$ involved in the $i{\text {{th}}}$ reaction chain is conserved and positive. If the set of initial concentrations of all the substrates, enzymes and intermediate complexes are given, the reactions will evolve in such a way that the conserved quantities remain conserved. When we say that there is a unique equilibrium in every positive compatibility class, it means that for a fixed set of values of the conserved quantities of a chemical reaction network, there exists only one positive vector of equilibrium concentrations that has the same values of the conserved quantities. Note that equilibrium concentrations are positive concentrations of the species of a reaction network at which the rates of change of the species concentrations are all zeros.

Further, it is shown in Conradi and Shiu (2015) that futile cycles of the type (2) governed by mass action kinetics are globally asymptotically stable. This has been proved using monotone systems theory (Angeli and Sontag 2008). In this paper, we prove the same result for a larger class of futile cycles given by (1). We first prove that (1) has a unique equilibrium in every positive compatibility class. This is proved in a simple way by first of all noting that the equilibrium concentrations of all the species are related, and hence one can obtain a polynomial equation in terms of the equilibrium concentration of one of the species in the network. We then make use of intermediate value property of continuous functions in order to prove the uniqueness of a positive equilibrium of this species and hence of all the other related species. For proving global asymptotic stability of futile cycle (1), we construct a Piecewise Linear in Rates (PWLR) Lyapunov Function. Such Lyapunov functions have been used to prove stability of chemical reaction networks recently in Blanchini and Giordano (2014) and Al-Radhawi and Angeli (2016). A piecewise linear Lyapunov function in the time-derivative of the states was also used to prove stability of nonlinear compartmental systems in Maeda et al. (1978) and Maeda and Kodama (1979).

Notation: The space of n dimensional real vectors is denoted by ${\mathbb {R}}^{{n}}$, and the space of ${m}\times {n}$ real matrices by ${\mathbb {R}}^{{m}\times {n}}$. The space of n dimensional real vectors consisting of all strictly positive entries is denoted by ${{\mathbb {R}}}_+^{n}$. ker(A) and im(A) denote the kernel and image of a real matrix A. $A^{\top }$ denotes the transpose of a matrix A. $y_i$ denotes the $i{\text {{th}}}$ component of a vector y. $0_{p,q}$ denotes a matrix of dimension $p\times q$ whose entries are all zeros. span(v) denotes the span of a real vector v.

2 Stoichiometry, positive compatibility class and conservation laws

In this section, we explain how to model the stoichiometry and how this can be used to derive the conservation laws of a chemical reaction network. Let us assume that a given chemical reaction network has $\rho$ reactions which could be a mix of reversible and irreversible chemical reactions. Let r denote the vector of reaction rates in the forward direction of the $\rho$ reactions. Let us assume that the reaction network involves $\mu$ chemical species and let x denote the vector of their concentrations. The dynamical equations for the chemical reaction network can be then obtained from the balance laws

$$\begin{aligned} \dot{x}:=\frac{dx}{dt}=Sr \end{aligned}$$

(3)

where $S\in {{\mathbb {R}}}^{\mu \times \rho }$ is called the stoichiometric matrix. Equation (3) holds for any chemical reaction network irrespective of the governing laws of its reactions. However r is a function of x and depends on the governing laws of the reactions in the network. We now show with the help of a simple example how the stochiometric matrix of a network can be constructed. Consider the reaction network

$$\begin{aligned}&X_1+3X_2\rightleftharpoons 2X_3 +X_4 \nonumber \\&X_3+2X_5\rightarrow X_6 \end{aligned}$$

(4)

The stoichiometric matrix maps the space of reaction rates to the space of species concentrations. Consequently, the entry of S corresponding to the $i{\text {{th}}}$ row and $j{{\text {th}}}$ column is the difference between the number of moles of the $i{\text {{th}}}$ species on the left hand and the right hand sides of the $j{{\text {th}}}$ reaction. For the reaction network (4), S is given by

$$\begin{aligned} S=\begin{bmatrix} -1&\quad 0 \\ -3&\quad 0 \\ 2&\quad -1 \\ 1&\quad 0 \\ 0&\quad -2 \\ 0&\quad 1 \end{bmatrix} \end{aligned}$$

The network is at equilibrium when $\dot{x}=0$. Let $r^*$ denote the vector of reaction rates (in the forward direction) of the network at an equilibrium. Then from Eq. (3), it follows that $r^*\in$ ker(S). Thus for the reaction network (4), $r_1^*=0$ and $r_2^*=0$.

Let $x_0 \in {{\mathbb {R}}}_+^{\mu }$ denote the vector of initial concentrations, i.e., $x_0=x|_{t=0}$. Then it is easy to see from Eq. (3) that

$$\begin{aligned} x-x_0 \in \text {im}(S) \end{aligned}$$

The space of concentrations

$$\begin{aligned} {\mathcal {S}}_{x_0}:=\{x \in {{\mathbb {R}}}_+^m \quad | \quad x-x_0 \in \text {im}(S)\} \end{aligned}$$

has been referred to as the positive reaction simplex in Horn and Jackson (1972) and the positive stoichiometric compatibility class (corresponding to $x_0$) in Feinberg (1995), Anderson (2011) and Siegel and MacLean (2000). In this paper we will use the terminology positive stoichiometric compatibility class to refer to ${\mathcal {S}}_{x_0}$.

Consider a vector $k \in$ ker$(S^{\top })$. This vector obeys the equation $k^{\top }\dot{x}=0$, consequently $k^{\top }x$ is a constant, meaning that $k^{\top }x=k^{\top }x_0$. The equation

$$\begin{aligned} k^{\top }x=\text {constant} \end{aligned}$$

is called a conservation law of the network. In general the number of linearly independent conservation laws is equal to the dimension of ker$(S^{\top })$.

Notice that the vector x stays in ${\mathcal {S}}_{x_0}$ as long as $x \in {{\mathbb {R}}}_+^m$ and $k^{\top }x=k^{\top }x_0$ for all vectors $k \in$ ker$(S^{\top })$.

Thus irrespective of the governing laws of a reaction network, based on the stoichiometry of the network, on the one hand, we can find the relation between reaction rates of the various reactions of the network at equilibrium by computing ker(S), and on the other hand, we can find all the conservation laws by computing ker$(S^\top )$. Below, we examine the former for the case of the reaction network (1) of interest.

Lemma 1

The futile cycle network (1) is at equilibrium if and only if the reaction rates (in the forward direction) of all the reactions of the network are equal.

Proof

To prove the lemma, we first need to construct the stoichiometric matrix for the network. The entries of the stoichiometric matrix depend on the ordering of the species and the reactions of the network. Let us order the species as in the following set.

$$\begin{aligned} \{P_0, P_1,\ldots ,P_{n-1},E_1,E_2,\ldots ,E_n,C_{11},C_{12},\ldots ,C_{1m_1},C_{21},\ldots ,C_{2m_2},\ldots ,\ldots ,C_{n_1},\ldots ,C_{nm_n}\} \end{aligned}$$

Let $R_{ij}$ denote the $j{{\text {th}}}$ reaction in the $i{\text {{th}}}$ reaction chain of the network and let $r_{ij}$ denote its rate. For the construction of the stoichiometric matrix, let us order the reactions of the network as in the following set.

$$\begin{aligned} \{R_{11},R_{12},\ldots ,R_{1(m_1+1)},R_{21},\ldots ,R_{2(m_2+1)},\ldots ,\ldots ,R_{n1},\ldots ,R_{n(m_n+1)}\} \end{aligned}$$

(5)

Let $\mathbf {e}_j$ denote the $j{{\text {th}}}$ element of the standard basis of the vector space ${{\mathbb {R}}}^n$. For $i=1,\ldots ,n-1$, define

$$\begin{aligned} {\mathcal {P}}_i:=\begin{bmatrix} -\mathbf {e}_i&0_{n,m_i-1}&\mathbf {e}_{i+1} \end{bmatrix} \end{aligned}$$

and define

$$\begin{aligned} {\mathcal {P}}_{n}:=\begin{bmatrix} -\mathbf {e}_n&0_{n,m_n-1}&\mathbf {e}_1 \end{bmatrix}. \end{aligned}$$

For $i=1,\ldots ,n$, define

$$\begin{aligned} {\mathcal {E}}_i:= \begin{bmatrix} -\mathbf {e}_i&0_{n,m_i-1}&\mathbf {e}_i \end{bmatrix}. \end{aligned}$$

For $i=1,\ldots ,n$, define ${\mathcal {C}}_{i}$ as a matrix of dimension $m_i \times (m_i+1)$ given by

$$\begin{aligned} {\mathcal {C}}_i:=\begin{bmatrix} 1&\quad -1&\quad 0&\quad 0&\quad \cdots&\quad 0&\quad 0\\ 0&\quad 1&\quad -1&\quad 0&\quad \cdots&\quad 0&\quad 0\\ 0&\quad 0&\quad 1&\quad -1&\quad \cdots&\quad 0&\quad 0\\ \vdots&\quad \vdots&\quad \vdots&\quad \ddots&\quad \ddots&\quad \vdots&\quad \vdots \\ 0&\quad 0&\quad 0&\quad 0&\quad \cdots&\quad 1&\quad -1\end{bmatrix}. \end{aligned}$$

Now define

$$\begin{aligned}&{\mathcal {P}}:=\begin{bmatrix} {\mathcal {P}}_1&{\mathcal {P}}_2&\cdots&{\mathcal {P}}_n \end{bmatrix}; \qquad {\mathcal {E}}:=\begin{bmatrix} {\mathcal {E}}_1&{\mathcal {E}}_2&\cdots&{\mathcal {E}}_n \end{bmatrix};\\&{\mathcal {C}}:=\begin{bmatrix} {\mathcal {C}}_1&\quad 0_{m_1,m_2+1}&\quad \cdots&\quad 0_{m_1,m_n+1}\\ 0_{m_2,m_1+1}&\quad {\mathcal {C}}_2&\quad \cdots&\quad 0_{m_2,m_n+1}\\ \vdots&\quad \vdots&\quad \ddots&\quad \vdots \\ 0_{m_n,m_1+1}&\quad 0_{m_n,m_2+1}&\quad \cdots&\quad {\mathcal {C}}_n \end{bmatrix}. \end{aligned}$$

The stoichiometric matrix S for the network (1) is then given by

$$\begin{aligned} S=\begin{bmatrix} {\mathcal {P}} \\ {\mathcal {E}} \\ {\mathcal {C}} \end{bmatrix}=\begin{bmatrix} {\mathcal {P}}_1&\quad {\mathcal {P}}_2&\quad \cdots&\quad {\mathcal {P}}_n\\ {\mathcal {E}}_1&\quad {\mathcal {E}}_2&\quad \cdots&\quad {\mathcal {E}}_n\\ {\mathcal {C}}_1&\quad 0_{m_1,m_2+1}&\quad \cdots&\quad 0_{m_1,m_n+1}\\ 0_{m_2,m_1+1}&\quad {\mathcal {C}}_2&\quad \cdots&\quad 0_{m_2,m_n+1}\\ \vdots&\quad \vdots&\quad \ddots&\quad \vdots \\ 0_{m_n,m_1+1}&\quad 0_{m_n,m_2+1}&\quad \cdots&\quad {\mathcal {C}}_n\end{bmatrix}. \end{aligned}$$

(6)

In order to prove the lemma, it suffices to prove that ker$(S)=$ span$(\mathbbm {1})$, where $\mathbbm {1}$ is a vector whose dimension is equal to the number of reactions in the network and each of whose entries is equal to 1. Let $r_{ij}^*$ $(j=1,\ldots ,m_i+1)$ denote the value of $r_{ij}$ at an equilibrium. Considering the ordering of reactions in (5), we have

$$\begin{aligned} r^*=[\begin{array}{cccccccccccc} r_{11}^*&r_{12}^*&\cdots&r_{1(m_1+1)}^*&r_{21}^*&\cdots&r_{2(m_2+1)}^*&\cdots&\cdots&r_{n1}^*&\cdots&r_{n(m_n+1)}^* \end{array}]^{\top } \in \text {ker}(S) \end{aligned}$$

It follows that ${\mathcal {C}}r^*=0$, which implies that

$$\begin{aligned} \begin{array}{ccccccccc} r_{11}^* &{}=&{} r_{12}^* &{}=&{} r_{13}^* &{}=&{} \cdots &{}=&{} r_{1(m_1+1)}^*;\\ r_{21}^* &{}=&{} r_{22}^* &{}=&{} r_{23}^*&{}=&{} \cdots &{}=&{} r_{2(m_2+1)}^*;\\ &{} &{} &{} &{} &{} &{} \vdots &{} &{} \\ r_{n1}^* &{}=&{} r_{n2}^* &{}=&{} r_{n3}^*&{}=&{} \cdots &{}=&{} r_{n(m_n+1)}^* \end{array} \end{aligned}$$

(7)

In words, in each chain of reactions in the network, the rates of all the individual reactions at equilibrium are equal. Since ${\mathcal {P}}r^*=0$, we get

$$\begin{aligned} r_{11}^*= & {} r_{n(m_n+1)}^*\nonumber \\ r_{21}^*= & {} r_{1(m_1+1)}^*\nonumber \\ r_{31}^*= & {} r_{2(m_2+1)}^*\nonumber \\&\vdots&\nonumber \\ r_{n1}^*= & {} r_{(n-1)(m_{n-1}+1)}^* \end{aligned}$$

(8)

Combining the sets of Eqs. (7) and (8), we get $r^* \in$ span$(\mathbbm {1})$. It is easy to verify that ${\mathcal {E}}v=0$ for any $v\in$ span$(\mathbbm {1})$, since every row of ${\mathcal {E}}$ has one entry equal to 1, another entry equal to $-1$ and the remaining entries equal to 0. This proves that ker$(S)=$ span$(\mathbbm {1})$. Hence the proof. $\square$

Using a similar method as in the proof above, one can also compute ker$(S^{\top })$ with S given by Eq. (6) and prove that the dimension of the ker$(S^{\top })$ is $n+1$. For $i=0,\ldots ,n-1$, let $\tilde{p}_i$ denote the concentration of $P_i$ and for $i=1,\ldots ,n$, let $\tilde{e}_i$ denote the concentration of $E_i$. For $i=1,\ldots ,n$, $j=1,\ldots ,m_i$, let $\tilde{c}_{ij}$ denote the concentration of the complex $C_{ij}$. Then the equations

$$\begin{aligned}&\displaystyle \sum _{i=0}^{n-1}\tilde{p}_i+\sum _{i=1}^{n}\sum _{j=1}^{m_i}\tilde{c}_{ij} = \alpha \end{aligned}$$

(9)

$$\begin{aligned}&\displaystyle \tilde{e}_i+\sum _{j=1}^{m_i}\tilde{c}_{ij} = \beta _i \quad (i=1,\ldots ,n). \end{aligned}$$

(10)

with real constants $\alpha$ and $\beta _i$ $(i=1,\ldots ,n)$, are $n+1$ linearly independent conserved quantities for the network.

3 Law of mass action kinetics

Recall that the reaction rates depend on the governing laws of the reactions of the network. We now describe this relation for mass action reaction networks, which are reaction networks, each of whose reactions is governed by the law of mass action kinetics. According to this law, the rate of a reaction is proportional to the concentrations of the different species on the substrate side of the reaction. For example, consider the reaction

$$\begin{aligned} X_1+X_2\overset{k_f}{\underset{k_r}{\rightleftharpoons }} X_3 \end{aligned}$$

(11)

In the reaction above, $k_f$ and $k_r$ are positive constants known as the forward and the reverse rate constants. Let $\tilde{x}_i$ denote the concentration of $X_i$ for $i=1,2,3$. The mass action reaction rate of the forward reaction is $k_f\tilde{x}_1\tilde{x}_2$, and the rate of the reverse reaction is $k_r\tilde{x}_3$. Therefore the overall reaction rate in the forward direction of the reversible reaction (11) is $r=k_f\tilde{x}_1\tilde{x}_2-k_r\tilde{x}_3$. Now consider the reversible reaction

$$\begin{aligned} 2Y_1+3Y_2 \overset{k_f}{\underset{k_r}{\rightleftharpoons }} Y_3+2Y_4 \end{aligned}$$

(12)

The above reaction can also be written as

$$\begin{aligned} Y_1+Y_1+Y_2+Y_2+Y_2 \overset{k_f}{\underset{k_r}{\rightleftharpoons }} Y_3+Y_4+Y_4 \end{aligned}$$

If $\tilde{y}_i$ denotes the concentration of the $Y_i$ for $i=1,\ldots ,4$, then the overall mass action reaction rate in the forward direction of the reversible reaction (12) is given by $r=k_f\tilde{y}_1^2\tilde{y}_2^3-k_r\tilde{y}_3\tilde{y}_4^2$.

Now consider the $i{\text {{th}}}$ reaction chain in the futile cycle network (1)

$$\begin{aligned} P_{i-1}+E_i \overset{k_{i1}}{\underset{k_{-i1}}{\rightleftharpoons }} C_{i1} \overset{k_{i2}}{\underset{k_{-i2}}{\rightleftharpoons }} C_{i2} \overset{k_{i3}}{\underset{k_{-i3}}{\rightleftharpoons }} \cdots \cdots \overset{k_{im_i}}{\underset{k_{-im_i}}{\rightleftharpoons }} C_{im_i} \overset{k_{i(m_i+1)}}{\longrightarrow } P_i+E_i \end{aligned}$$

Assuming that the governing law of each reaction is mass action kinetics, with $r_{ij}$ as defined earlier, we get

$$\begin{aligned} r_{i1}= & {} k_{i1}\tilde{p}_{i-1}\tilde{e}_i-k_{-i1}\tilde{c}_{i1}\nonumber \\ r_{i2}= & {} k_{i2}\tilde{c}_{i1}-k_{-i2}\tilde{c}_{i2} \nonumber \\&\vdots&\nonumber \\ r_{im_i}= & {} k_{im_i}\tilde{c}_{i(m_i-1)}-k_{-im_i}\tilde{c}_{im_i} \nonumber \\ r_{i(m_i+1)}= & {} k_{i(m_i+1)}\tilde{c}_{im_i} \end{aligned}$$

(13)

Using Eqs. (3), (6) and (13), we get the following set of equations describing the rate of change of concentrations of the different species involved in the network (1):

$$\begin{aligned} \frac{d\tilde{p}_0}{dt}= & {} k_{n(m_n+1)}\tilde{c}_{nm_n}-k_{11}\tilde{p}_0\tilde{e}_{1}+k_{-11}\tilde{c}_{11} \nonumber \\ \frac{d\tilde{p}_i}{dt}= & {} k_{i(m_i+1)}\tilde{c}_{im_i}-k_{(i+1)1}\tilde{p}_i\tilde{e}_{i+1}+k_{-(i+1)1}\tilde{c}_{(i+1)1} \qquad \text {for} \quad i=1,\dots ,n-1 \nonumber \\ \frac{d\tilde{c}_{i1}}{dt}= & {} k_{i1}\tilde{p}_{i-1}\tilde{e}_{i}+k_{-i2}\tilde{c}_{i2}-(k_{-i1}+k_{i2})\tilde{c}_{i1} \qquad \text {for} \quad i=1,\dots ,n \nonumber \\ \frac{d\tilde{c}_{im_i}}{dt}= & {} k_{im_i}\tilde{c}_{i(m_i-1)}-(k_{-im_i}+k_{im_i+1})\tilde{c}_{im_i} \qquad \text {for} \quad i=1,\dots ,n\nonumber \\ \frac{d\tilde{c}_{ij}}{dt}= & {} k_{ij}\tilde{c}_{i(j-1)}+k_{-i(j+1)}\tilde{c}_{i(j+1)}-(k_{i(j+1)}+k_{-ij})\tilde{c}_{ij}\nonumber \\&\quad \text {for} \quad j=2,\ldots ,m_i-1, \quad i=1,\ldots ,n \nonumber \\ \frac{d\tilde{e}_i}{dt}= & {} -k_{i1}\tilde{p}_{i-1}\tilde{e}_i+k_{-i1}\tilde{c}_{i1}+k_{i(m_i+1)}c_{im_i} \quad \text {for} \quad i=1,\dots ,n. \end{aligned}$$

(14)

4 Uniqueness of equilibrium

In this section, we prove that the futile cycle (1) has a unique equilibrium in every positive compatibility class. This proof requires that the nonnegative orthant is invariant with respect to the dynamical equations corresponding to the futile cycle network (1). This property commonly referred to as nonegativity is well known for all mass action reaction networks. The reader is referred to (Vol’pert and Hudjaev 1985, pp. 613–615) for a simple proof of nonnegativity of mass action chemical reaction networks. For the sake of completeness, we provide an alternate proof of nonnegativity specifically for the case of the network of interest.

Lemma 2

If the initial concentration of each of the species of the futile cycle network (1) governed by mass action kinetics is nonnegative, then it remains nonnegative at all future times.

Proof

Note that all the forward and the reverse rate constants of the reactions in the network are positive. If we assume that at a particular instant of time, one of the species of the network has zero concentration and the rest have nonnegative concentrations, then from Eq. (14), it follows that the time derivative of the species with zero instantaneous concentration is nonnegative. This proves that the nonnegative orthant is invariant with respect to the differential equations (14), since any point on the boundary of the nonnegative orthant will either be pushed into the positive orthant or will stay in the boundary. In other words, if the initial concentrations are nonnegative, they remain nonnegative at all times. $\square$

Hereafter in all the analysis with respect to the mass action chemical reaction network (1) that follows, it will be assumed that the initial concentrations of $P_0$, $E_i$, $i=1,\ldots ,n$ are positive and the initial concentrations of the remaining species of the network are nonnegative. This ensures that with respect to the conservation laws (9) and (10), we have $\alpha >0$ and $\beta _i>0$ for $i=1,\ldots ,n$. Further $p_i$, $e_i$ and $c_{ij}$ will be used to denote the concentrations of $P_i$, $E_i$ and $C_{ij}$ respectively at an equilibrium.

In order to prove the uniqueness of equilibrium in each positive compatibility class, we need to be able to parametrize the equilibrium concentrations of all the species of the network in terms of the equilibrium concentration of one particular species. Below we prove that such a parametrization is possible.

Lemma 3

Choose a $q \in \{1,2,\ldots ,n\}$. For each $i\in \{1,\ldots ,n\}$, there exist constants $a_i\in {{\mathbb {R}}}_+$, $b_i\in {{\mathbb {R}}}_+$ and $\delta _{ij}\in {{\mathbb {R}}}_+$, $j\in \{1,\ldots ,m_i\}$, such that

$$\begin{aligned} c_{ij}= & {} \frac{\delta _{ij}k_{q(m_q+1)}c_{qm_q}}{k_{i(m_i+1)}} \end{aligned}$$

(15)

$$\begin{aligned} p_{i-1}= & {} \frac{a_ik_{q(m_q+1)}c_{qm_q}}{b_ik_{i(m_i+1)}-k_{q(m_q+1)}c_{qm_q}} \end{aligned}$$

(16)

$$\begin{aligned} e_i= & {} \left( b_i-\frac{k_{q(m_q+1)}c_{qm_q}}{k_{i(m_i+1)}}\right) \sum _{j=1}^{m_i}\delta _{ij} \end{aligned}$$

(17)

where $k_{ij}$ denotes the mass action forward rate constant of the $j{{\text {th}}}$ reaction in the $i{\text {{th}}}$ reaction chain of the futile cycle network (1).

Proof

Lemma 1 states that at equilibrium, the overall reaction rate in the forward direction of each of the reversible reactions and the reaction rates of each of the irreversible reactions in (1) are equal to each other. This implies by virtue of equations (13) that

$$\begin{aligned} k_{i1}p_{i-1}e_i-k_{-i1}c_{i1}= & {} k_{i2}c_{i1}-k_{-i2}c_{i2}=\cdots \cdots =k_{im_i}c_{i(m_i-1)}-k_{-im_i}c_{im_i} \nonumber \\= & {} k_{i(m_i+1)}c_{im_i} \end{aligned}$$

(18)

for $i=1,\ldots ,n$ and

$$\begin{aligned} k_{1(m_1+1)}c_{1m_1}=k_{2(m_2+1)}c_{2m_2}=\cdots =k_{n(m_n+1)}c_{nm_n}. \end{aligned}$$

(19)

For $j=1,\ldots ,m_i$, we prove by induction that there exists a $\delta _{ij} \in {{\mathbb {R}}}_+$, such that

$$\begin{aligned} c_{ij}=\delta _{ij}c_{im_i}. \end{aligned}$$

(20)

Note that $\delta _{im_i}=1>0$. Assume that $c_{i(j+1)}=\delta _{i(j+1)}c_{im_i}$ with $\delta _{i(j+1)}>0$ and $j\le m_i-1$. Then from Eq. (18), it follows that

$$\begin{aligned} k_{i(j+1)}c_{ij}-k_{-i(j+1)}c_{i(j+1)}=k_{i(m_i+1)}c_{im_i}. \end{aligned}$$

This implies that

$$\begin{aligned} c_{ij}=\frac{1}{k_{i(j+1)}}(k_{i(m_i+1)}+k_{-i(j+1)}\delta _{i(j+1)})c_{im_i}=\delta _{ij}c_{im_i} \end{aligned}$$

where

$$\begin{aligned} \delta _{ij}:=\frac{1}{k_{i(j+1)}}(k_{i(m_i+1)}+k_{-i(j+1)}\delta _{i(j+1)}). \end{aligned}$$

It follows that $\delta _{ij}>0$ if $\delta _{i(j+1)}>0$. Since $\delta _{im_i}>0$, by induction, we obtain $\delta _{ij}>0$ for $i=1,2,\ldots ,m_{i}-1$.

From Eq. (18), it also follows that

$$\begin{aligned} k_{i1}p_{i-1}e_i-k_{-i1}c_{i1}=k_{i(m_i+1)}c_{im_i}. \end{aligned}$$

This implies that

$$\begin{aligned} p_{i-1}e_i=\frac{1}{k_{i1}}(k_{i(m_i+1)}+k_{-i1}\delta _{i1})c_{im_i}=\delta _{i0}c_{im_i} \end{aligned}$$

(21)

where

$$\begin{aligned} \delta _{i0}:=\frac{1}{k_{i1}}(k_{i(m_i+1)}+k_{-i1}\delta _{i1})>0. \end{aligned}$$

Taking into account the fact that the conservation law (10) holds also for equilibrium concentrations, we have

$$\begin{aligned} p_{i-1}=\frac{\delta _{i0}c_{im_i}}{e_i}=\frac{\delta _{i0}c_{im_i}}{\beta _i-\sum _{j=1}^{m_i}c_{ij}}=\frac{\delta _{i0}c_{im_i}}{\beta _i-c_{im_i}\sum _{j=1}^{m_i}\delta _{ij}} \end{aligned}$$

(22)

where $\delta _{im_i}:=1$ for $i=1,\ldots ,n$. Define for $i=1,\ldots ,n$, the positive constants

$$\begin{aligned} a_i:=\frac{\delta _{i0}}{\sum _{j=1}^{m_i}\delta _{ij}}; \qquad \qquad b_i:=\frac{\beta _i}{\sum _{j=1}^{m_i}\delta _{ij}}. \end{aligned}$$

Then from Eq. (22),

$$\begin{aligned}&\displaystyle p_{i-1}=\frac{a_ic_{im_i}}{b_i-c_{im_i}} \end{aligned}$$

(23)

$$\begin{aligned}&\displaystyle e_i = \big (b_i-c_{im_i})\sum _{j=1}^{m_i}\delta _{ij}. \end{aligned}$$

(24)

If we choose a $q\in \{1,\ldots ,n\}$, from Eq. (19), we have

$$\begin{aligned} c_{im_i}=\frac{k_{q(m_q+1)}c_{qm_q}}{k_{i(m_i+1)}}. \end{aligned}$$

(25)

Substituting for $c_{im_i}$ as given by the above equation in Eqs. (20), (23) and (24) results in Eqs. (15), (16) and (17) respectively. $\square$

We now prove that the futile cycle (1) cannot have any boundary equilibrium.

Lemma 4

At an equilibrium of the mass action futile cycle network (1), none of the species concentrations is zero.

Proof

We use the parametrization of Lemma 3 for the proof. As mentioned earlier, with reference to the conservation laws (9) and (10), $\alpha >0$ and $\beta _i>0$ for $i=1,\ldots ,n$. If we assume that $c_{ij}=0$ for some admissible numbers i, j, then from Eqs. (15) and (16), it follows that the equilibrium concentrations of all substrates and complexes are zeros. Since the conservation law (9) holds also for equilibrium concentrations, it follows that $\alpha =0$, which leads to a contradiction. Assuming that $p_i=0$ for some $i\in \{0,\ldots ,n-1\}$ leads to a similar contradiction. If we assume that $e_i=0$ for some $i\in \{1,\ldots ,n\}$, then from Eq. (17), it follows that

$$\begin{aligned} b_ik_{i(m_i+1)}=k_{q(m_q+1)}c_{qm_q} \end{aligned}$$

From Lemma 2 and conservation law (9), we have $0\le p_{i-1}<\alpha$. Owing to the finiteness of $p_{i-1}$, from Eq. (16), it follows that $c_{qm_q}=0$, which leads to a similar contradiction as before. Hence, the futile cycle (1) cannot have any boundary equilibrium. $\square$

Remark 5

Lemma 4 can be also proved using (Vol’pert and Hudjaev 1985, Theorem 1, p. 617) related to positivity of reachable species in a chemical reaction network. This method has been used in Siegel and MacLean (2000) in order to prove the nonexistence of boundary equilibria in enzyme kinetic reaction networks that are similar to but simpler than the network (1). We briefly explain the concept of reachability as in Vol’pert and Hudjaev (1985). Assume that $\alpha$ species ${\mathfrak {S}}_1,\ldots , {\mathfrak {S}}_{\alpha }$ of a network have nonzero initial concentrations and the rest have zero initial concentrations. Let $A_0$ denote the set of species with nonzero initial concentrations.

$$\begin{aligned} A_0:=\{{\mathfrak {S}}_0,{\mathfrak {S}}_2,\ldots ,{\mathfrak {S}}_{\alpha }\} \end{aligned}$$

(26)

Now consider all the reactions whose substrates consist only of species contained in $A_0$. Let $A_1$ denote the set of all those species that are products of such reactions. Note that in this step, the forward and the reverse parts of each reversible reaction must be considered as two separate reactions. Now update the set $A_0$ as $A_0= A_0 \cup A_1$ and repeat the process described below Eq. (26) until $A_0$ cannot be updated with new species anymore. At this point, all the species that are not contained in $A_0$ are said to be unreachable from the species in the initial set

$$\begin{aligned} \{{\mathfrak {S}}_0,{\mathfrak {S}}_2,\ldots ,{\mathfrak {S}}_{\alpha }\}. \end{aligned}$$

(27)

(Vol’pert and Hudjaev 1985, Theorem 1, p. 617) states that all species that are unreachable from the set (27) have zero concentrations at all times. If we assume that for the network (1) under consideration, we begin with equilibrium concentrations of species, then all species must remain at the same equilibrium concentrations. Now assume that $c_{ij}=0$ for some admissible i and j. Then by (Vol’pert and Hudjaev 1985, Theorem 1, p. 617), $C_{ij}$ is unreachable from the set of species with nonzero equilibrium concentrations. Thus $c_{ik}=0$ for $k=1,\ldots ,m_i$ and either $e_i=0$ or $p_{i-1}=0$. $e_i=0$ violates the conservation law (10), since it is assumed that $\alpha>0, \beta _i>0, i=1,\ldots ,n$. Hence $p_{i-1}=0$. This implies that $c_{\eta j}=0$ for $j=1,\ldots ,m_{\eta }$, where $\eta =i-1$ if $i\ne 1$ and $\eta =n$ otherwise. This in turn implies that $p_l=0$ and $c_{lk}=0$ for all admissible l and k. However this violates conservation law (9), since $\alpha >0$. Thus all intermediate complexes $C_{lk}$ have nonzero equilibrium concentrations. In a similar way, it can be proved that $p_{i-1}\ne 0$ and $e_i\ne 0$ for $i=1,\ldots ,n$.

We now prove the main result of this section pertaining to the uniqueness of equilibrium in every positive compatibility class.

Theorem 6

The mass action chemical reaction network (1) has a unique equilibrium in every positive compatibility class.

Proof

We use the parametrization of Lemma 3 for the proof. Since the conservation law (9) holds also for equilibrium concentrations, substituting Eqs. (15) and (16) in the conservation law (9), we get

$$\begin{aligned} k_{q(m_q+1)}c_{qm_q}\sum _{i=1}^{n}\left( \frac{\sum _{j=1}^{m_i}\delta _{ij}}{k_{i(m_i+1)}}\right) +\sum _{i=1}^{n}\frac{a_ik_{q(m_q+1)}c_{qm_q}}{b_ik_{i(m_i+1)}-k_{q(m_q+1)}c_{qm_q}}=\alpha \end{aligned}$$

(28)

The above equation is in terms of only one unknown $c_{qm_q}$. Consider the numbers $d_i:=k_{i(m_i+1)}b_i$, $i=1,\ldots ,n$. Since the choice of q in Lemma 3 is arbitrary, let q denote the index for which $d_q$ is minimum among the elements of $\{d_1,d_2,\ldots ,d_n\}$. Now define the positive constants

$$\begin{aligned} t:=k_{q(m_q+1)}\sum _{i=1}^{n}\left( \frac{\sum _{j=1}^{m_i}\delta _{ij}}{k_{i(m_i+1)}}\right) \qquad \qquad v_i:=\frac{b_ik_{i(m_i+1)}}{k_{q(m_q+1)}} \end{aligned}$$

(29)

Observe that $v_q=b_q$ and $v_i\ge b_q$ $\forall$ $i \in \{1,\ldots ,n\}$. Substituting (29) in (28), we get

$$\begin{aligned} tc_{qm_q}+\sum _{i=1}^{n}\frac{a_ic_{qm_q}}{v_i-c_{qm_q}}=\alpha \end{aligned}$$

(30)

From Lemmas 2 and 4, it follows that the equilibrium concentration of each of the species is positive. Thus $e_q>0$, and consequently from Eq. (17), it follows that $c_{qm_q}<b_q$. We now prove that Eq. (30) in the unknown $c_{qm_q}$ has precisely one real root in the admissible open interval $(0,b_q)$. The proof is based on the intermediate value property of continuous real valued functions. Define

$$\begin{aligned} \Phi (x):=tx-\alpha +\sum _{i=1}^{n}\frac{a_ix}{v_i-x} \end{aligned}$$

Assume that $v_i=b_q$ for exactly k values of $i \in \{1,2,\ldots ,n\}\backslash \{q\}$. For the remaining values of $i\in \{1,2,\ldots ,n\}\backslash \{q\}$, $v_i>b_q$. Note that $0 \le k \le n-1$. Without loss of generality assume that $v_i=b_q$ for $i=n-k+1,n-k+2,\ldots ,n$ and $q=n-k$. Define

$$\begin{aligned} \nu (x):= & {} \Phi (x)\prod _{i=1}^{n-k}(v_i-x)=(tx-\alpha )\prod _{i=1}^{n-k}(v_i-x)\\&+ \, x(b_q-x)\sum _{i=1}^{n-k-1}\left( a_i\prod _{l=1, l\ne i}^{n-k-1}(v_l-x)\right) +x\prod _{l=1}^{n-k-1}(v_l-x)\sum _{i=n-k}^{n}a_i \end{aligned}$$

and note that $\nu$ is a continuous function in the closed interval $[0,b_q]$. Observe that

$$\begin{aligned} \nu (0)=-\alpha \prod _{i=1}^{n-k}v_i<0 \end{aligned}$$

and

$$\begin{aligned} \nu (b_q)=b_q\prod _{l=1}^{n-k-1}(v_l-b_q)\sum _{i=n-k}^{n}a_i>0. \end{aligned}$$

This implies that there is at least one root of $\nu$ in the interval $(0,b_q)$. We prove that there is exactly one root in this interval. Assume by contradiction that there are at least two roots $x_1$, $x_2$ of $\nu$ in the interval $(0,b_q)$. Then $\nu (x_1)=0$ and $\nu (x_2)=0$. Since $v_i\ge b_q$ for $i \in \{1,2,\ldots ,n-k\}$, this implies that

$$\begin{aligned}&\displaystyle \Phi (x_1)=\Phi (x_2)=0\nonumber \\&\displaystyle tx_1-\alpha +\sum _{i}\frac{a_i}{\frac{v_i}{x_1}-1}=0 \end{aligned}$$

(31)

$$\begin{aligned}&\displaystyle tx_2-\alpha +\sum _{i}\frac{a_i}{\frac{v_i}{x_2}-1}=0 \end{aligned}$$

(32)

Subtracting Eqs. (32) from (31), we get

$$\begin{aligned} t(x_1-x_2)+\sum _ia_i\left( \frac{1}{\frac{v_i}{x_1}-1}-\frac{1}{\frac{v_i}{x_2}-1}\right) =0 \end{aligned}$$

(33)

If $x_1>x_2$, then

$$\begin{aligned}&\displaystyle t(x_1-x_2)>0 \end{aligned}$$

(34)

$$\begin{aligned}&\displaystyle a_i\left[ \frac{1}{\frac{v_i}{x_1}-1}-\frac{1}{\frac{v_i}{x_2}-1}\right] >0 \end{aligned}$$

(35)

Notice that (33), (34) and (35) lead to a contradiction. A similar contradiction can be obtained if we assume that $x_2>x_1$. This implies that $x_1=x_2$, in other words, there is exactly one root of $\nu$ in the interval $(0,b_q)$. This in turn implies that there is exactly one root of $\Phi$ in the interval $(0,b_q)$.

It follows that Eq. (30) in the unknown $c_{qm_q}$ has exactly one real root in the admissible open interval $(0,b_q)$. This implies that in a particular positive compatibility class, the equilibrium concentration $c_{qm_q}$ is unique and positive. From Lemma 3, it follows that the equilibrium concentrations of all the remaining species of the futile cycle are unique and positive in a particular positive compatibility class (with $\alpha ,\beta _i>0$). $\square$

5 Global stability

We are now in a position to prove the global stability of futile cycle network (1). As mentioned in the introduction, for this purpose, we make use of a PWLR Lyapunov function coupled with LaSalle’s invariance principle (LaSalle 1960; Khalil 2014, Section 4.2, Murray et al. 1994, pp. 188–189).

Theorem 7

All solution trajectories to the set of Eq. (14) that belong to a particular positive stoichiometric compatibility class asymptotically converge to the unique equilibrium in that stoichiometric compatibility class.

Proof

Note that the set of Eq. (14) describes the rate of change of concentrations of the different species in the futile cycle network (1). With respect to this network, let r denote the vector of all the reaction rates $r_{ij}$ as defined in Sect. 3. We now define the PWLR Lyapunov function

$$\begin{aligned} V(r)=\Vert r\Vert _{\infty }=\max _{1\le i\le n}\max _{1\le j\le m_i+1}|r_{ij}| \end{aligned}$$

It is easy to see that V is a piecewise linear function of the components of r. Observe that V(r) is continuous in time, since each component of r is continuous in time. We consider three possible cases below and prove that $\frac{d}{dt}V(r)\le 0$ for each of the three cases.

Case 1: $\Vert r\Vert _{\infty }=|r_{i1}|$ for some $i\in \{1,\ldots ,n\}$ in the time-interval $t_0<t\le t_1$.

As in (13), we have

$$\begin{aligned} r_{i1} = k_{i1}\tilde{p}_{i-1}\tilde{e}_i-k_{-i1}\tilde{c}_{i1} \end{aligned}$$

In case, $r_{i1} > 0$,

$$\begin{aligned} \frac{d}{dt}|r_{i1}|= & {} k_{i1}\tilde{p}_{i-1}\frac{d\tilde{e}_i}{dt}+k_{i1}\tilde{e}_{i}\frac{d\tilde{p}_{i-1}}{dt}-k_{-i1}\frac{d\tilde{c}_{i1}}{dt}\\= & {} k_{i1}\tilde{p}_{i-1}(r_{im_i+1}-r_{i1})+k_{i1}\tilde{e}_{i}(r_{i-1m_{i}+1}-r_{i1})+k_{-i1}(r_{i2}-r_{i1}) \end{aligned}$$

Since $r_{i1}>0$ and $\Vert r\Vert _{\infty }=r_{i1}$, it follows

$$\begin{aligned} \frac{d}{dt}V(r)=\frac{d}{dt}r_{i1}\le 0 \end{aligned}$$

with the equality occuring if $r_{i1}=r_{im_i+1}=r_{i-1m_{i}+1}=r_{i2}$.

In case $r_{ij}<0$, we have

$$\begin{aligned} \frac{d}{dt}|r_{i1}|=k_{i1}\tilde{p}_{i-1}(r_{i1}-r_{im_i+1})+k_{i1}\tilde{e}_{i}(r_{i1}-r_{i-1m_{i}+1})+k_{i1}(r_{i1}-r_{i2}) \end{aligned}$$

In this case $\Vert r\Vert _{\infty }=-r_{i1}$ and hence again

$$\begin{aligned} \frac{d}{dt}V(r)=-\frac{d}{dt}r_{i1} \le 0 \end{aligned}$$

with the equality occuring if $r_{i1}=r_{i2}$, $\tilde{p}_{i-1}(r_{i1}-r_{im_i+1})=0$ and $\tilde{e}_{i}(r_{i1}-r_{i-1m_{i}+1})=0$.

In case $r_{i1}=0$, we have $r=0$, which implies (from Eq. (13)) that the concentrations of each of the species in the network is zero, which is not possible since it violates the conservation laws (9), (10). Thus

$$\begin{aligned} \frac{d}{dt}V(r)=\frac{d}{dt}|r_{i1}| \le 0 \end{aligned}$$

in the time interval $t_0<t \le t_1$.

Case 2: $\Vert r\Vert _{\infty }=|r_{im_i+1}|$ for some $i\in \{1,\ldots ,n\}$ in the time-interval $t_0<t\le t_1$. As in (13), $r_{i(m_i+1)}=k_{i(m_i+1)}\tilde{c}_{im_i}\ge 0$. We have $r_{i(m_i+1)}\ne 0$, since $r_{i(m_i+1)}= 0$ implies that $r=0$ leading to all the concentrations being equal to zero as described earlier. Hence $r_{i(m_i+1)}> 0$. Since the rate of the reaction

$$\begin{aligned} C_{im_i}\longrightarrow P_i+E_i \end{aligned}$$

is greater than or equal to that of any other reaction in the network, in particular of the reaction $C_{im_i-1}\rightleftharpoons C_{im_i}$, it follows that $\frac{d}{dt}\Vert r\Vert _{\infty }=k_{i(m_i+1)}\frac{d\tilde{c}_{im_i}}{dt} \le 0$. Thus

$$\begin{aligned} \frac{d}{dt}V(r)=\frac{d}{dt}r_{im_i+1} \le 0 \end{aligned}$$

in the time interval $t_0<t \le t_1$ with equality occuring if $r_{im_i}=r_{im_i+1}$.

Case 3: $\Vert r\Vert _{\infty }=|r_{ij}|$ with $1<j<m_i+1$. As in (13), we have

$$\begin{aligned} r_{ij} = k_{ij}\tilde{c}_{i\,j-1}-k_{-ij}\tilde{c}_{ij} \end{aligned}$$

As in the other cases, we cannot have $r_{ij}=0$. In both the cases, $r_{ij}>0$ and $r_{ij}<0$, we can prove that $\frac{d}{dt}V(r)=\frac{d}{dt}|r_{ij}| \le 0$ as in Case 1 with the equality occuring if $r_{i(j-1)}=r_{ij}=r_{i(j+1)}$. Thus

$$\begin{aligned} \frac{d}{dt}V(r)=\frac{d}{dt}|r_{ij}| \le 0 \end{aligned}$$

in the time interval $t_0<t \le t_1$.

Let $\mathfrak {E}$ denote the set of all vectors r for which $\frac{d}{dt}V(r)=0$. In all the three cases considered above, it can be proved that any $r\in \mathfrak {E}$ that is positively invariant satisfies $r \in$ span$(\mathbbm {1})$ where, as before $\mathbbm {1}$ denotes a vector with the same dimension as r that has every entry equal to 1. In the following, we prove this for Case 1. For the remaining 2 cases, the proof is similar.

For Case 1, as proved above, $[\frac{d}{dt}V(r)=0] \Longrightarrow [r_{i1}=r_{i2}]$. This implies that $\frac{d\tilde{c}_{i1}}{dt}=0$. For invariance, we need to have

$$\begin{aligned} \frac{dr_{i1}}{dt}=\frac{dr_{i2}}{dt}=0. \end{aligned}$$

Consequently

$$\begin{aligned} \frac{dr_{i2}}{dt}=k_{i2}\frac{d\tilde{c}_{i1}}{dt}-k_{-i2}\frac{d\tilde{c}_{i2}}{dt}=-k_{-i2}\frac{d\tilde{c}_{i2}}{dt}=0 \end{aligned}$$

This implies that $\frac{d\tilde{c}_{i2}}{dt}=0$, which in turn implies that $r_{i2}=r_{i3}$ and $\frac{dr_{i3}}{dt}=0$. Thus by induction, it follows that

$$\begin{aligned} r_{i1}=r_{i2}=\cdots =r_{i(m_{i}+1)}=\text {a constant} \end{aligned}$$

This implies that

$$\begin{aligned} \frac{d\tilde{c}_{i1}}{dt}=\frac{d\tilde{c}_{i2}}{dt}=\cdots =\frac{d\tilde{c}_{im_i}}{dt}=0 \end{aligned}$$

From conservation law (10), it follows that $\frac{d\tilde{e}_{i}}{dt}=0$. Now

$$\begin{aligned} \frac{dr_{i1}}{dt}=k_{i1}\tilde{p}_{i-1}\frac{d\tilde{e}_i}{dt}+k_{i1}\tilde{e}_i\frac{d\tilde{p}_{i-1}}{dt}=k_{i1}\tilde{e}_i\frac{d\tilde{p}_{i-1}}{dt}=k_{i1}\tilde{e}_i(r_{(i-1)(m_{i-1}+1)}-r_{i1})=0 \end{aligned}$$

(36)

If we assume that $\tilde{e}_i=0$, then

$$\begin{aligned} \frac{d\tilde{e}_i}{dt}=-k_{i1}\tilde{p}_{i-1}\tilde{e}_i+k_{-i1}\tilde{c}_{i1}+k_{i(m_{i}+1)}\tilde{c}_{im_i}=k_{-i1}\tilde{c}_{i1}+k_{i(m_{i}+1)}\tilde{c}_{im_i}=0 \end{aligned}$$

and the nonnegativity of species concentrations by Lemma 2 imply that $\tilde{c}_{i1}=\tilde{c}_{im_i}=0$. This in turn implies that $\Vert r\Vert _{\infty }=|r_{i1}|=0$. However as mentioned earlier, this is not possible since it is equivalent with all the species concentrations being equal to zero violating the conservation laws. Thus $\tilde{e}_i\ne 0$. From Eq. (36), it follows that $r_{i1}=r_{(i-1)(m_{i-1}+1)}$. For invariance, we need to have

$$\begin{aligned} \frac{dr_{(i-1)(m_{i-1}+1)}}{dt}= & {} k_{(i-1)(m_{i-1}+1)}\frac{d\tilde{c}_{i-1\,m_{i-1}}}{dt}\\= & {} k_{(i-1)(m_{i-1}+1)}(r_{(i-1)(m_{i-1})}-r_{(i-1)(m_{i-1}+1)})=0 \end{aligned}$$

This implies that $r_{(i-1)(m_{i-1})}=r_{(i-1)(m_{i-1}+1)}$. By induction, it follows that $r\in$ span$(\mathbbm {1})$ for Case 1. By a similar reasoning, it follows that any $r\in \mathfrak {E}$ that is positively invariant satisfies $r \in$ span$(\mathbbm {1})$ for Case 2 and Case 3 as well.

From Lemma 1 and Theorem 6, it follows that for a given initial concentration vector $x_0$, the only vector $r \in \mathfrak {E}$ that is positively invariant corresponds to the unique equilibrium concentration $x^* \in {\mathcal {S}}_{x_0}$, where ${\mathcal {S}}_{x_0}$ denotes the positive compatibility class corresponding to $x_0$. Since $\frac{d}{dt}V(r)\le 0$ and r is a continuous function of the concentration vector x, by LaSalle’s invariance principle, it follows that every $x \in {\mathcal {S}}_{x_0}$ asymptotically converges to $x^*$. $\square$

6 Conclusion

We have proved the global asymptotic stability of a special class of futile cycle networks which includes the model of processive multisite phosphorylation networks described in Conradi and Shiu (2015). We used a simple algebraic method based on intermediate value property of continuous functions in order to prove the existence of a unique equilibrium concentration vector in every positive compatibility class. Furthermore, we constructed a piecewise linear in rates (PWLR) Lyapunov function in order to prove the global asymptotic stability of this equilibrium vector. This construction is inspired by the recent work in Al-Radhawi and Angeli (2016), where a systematic approach towards the construction of PWLR Lyapunov functions in order to prove stability of certain chemical reaction networks is described. Current research is focused on the direction of using the special Lyapunov function described in this paper to prove stability of a larger class of chemical reaction networks.