Theory of a microfluidic serial dilution bioreactor for growth of planktonic and biofilm populations

Abstract

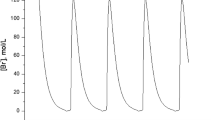
We present the theory of a microfluidic bioreactor with a two-compartment growth chamber and periodic serial dilution. In the model, coexisting planktonic and biofilm populations exchange by adsorption and detachment. The criteria for coexistence and global extinction are determined by stability analysis of the global extinction state. Stability analysis yields the operating diagram in terms of the dilution and removal ratios, constrained by the plumbing action of the bioreactor. The special case of equal uptake function and logistic growth is analytically solved and explicit growth curves are plotted. The presented theory is applicable to generic microfluidic bioreactors with discrete growth chambers and periodic dilution at discrete time points. Therefore, the theory is expected to assist the design of microfluidic devices for investigating microbial competition and microbial biofilm growth under serial dilution conditions.

Appendices

Appendix A: Stability analysis

We can rewrite the initial value problem in Eq. (2.1) in vector form

$$\begin{aligned} \frac{dX}{dt}= & {} F(X)\nonumber \\ X(0)= & {} x_{0} \end{aligned}$$

(5.1)

where the vector X and F(X) are defined as

$$\begin{aligned} X= \begin{pmatrix} S \\ u \\ w \end{pmatrix}\!,\,\,\, F(X)= \begin{pmatrix} -\frac{1}{\gamma }f_{u}(S)u-\frac{\delta }{\gamma }f_{w}(S)w \\ (f_{u}(S)-\alpha )u+\delta \beta w\\ (f_{w}(S)-\beta )w+\frac{\alpha u}{\delta }\\ \end{pmatrix} \end{aligned}$$

Then we have

$$\begin{aligned} \frac{d}{dt}\Phi _{t}(x_{0})=F(\Phi _{t}(x_{0})),\quad \Phi _{0}(x_{0})\equiv x_{0} \end{aligned}$$

(5.2)

Differentiating Eq. (5.2) with respect to $x_{0}\in {\mathbf {R}}^{3}$ yields

$$\begin{aligned} \frac{d}{dt}D_{x_{0}}\Phi _{t}(x_{0})= & {} D_{x}F(\Phi _{t}(x_{0})) D_{x_{0}}\Phi _{t}(x_{0})\nonumber \\ D_{x_{0}}\Phi _{0}(x_{0})= & {} I \end{aligned}$$

(5.3)

Setting $x_{0}=(\tilde{S},0,0)$ in Eq. (5.3), then we obtain

$$\begin{aligned} \frac{d}{dt}V(t)= & {} AV(t) \nonumber \\ V(0)= & {} I \end{aligned}$$

(5.4)

where $V(t)=D_{x_{0}}\Phi _{t}(x_{0})\bigg |_{x_{0}=(\tilde{S},0,0)}$ and

$$\begin{aligned} A= \begin{pmatrix} -\frac{u}{\gamma }f_{u}'(S)-\frac{\delta w}{\gamma }f_{w}'(S) &{}\quad -\frac{1}{\gamma }f_{u}(S) &{}\quad -\frac{\delta }{\gamma }f_{w}(S)\\ f_{u}'(S)u &{}\quad f_{u}(S)-\alpha &{}\quad \beta \delta \\ f_{w}'(S)w &{}\quad \alpha \delta ^{-1} &{}\quad f_{w}(S)-\beta \end{pmatrix} \end{aligned}$$

(5.5)

Substituting $(S,u,w)=\Phi _{t}(\tilde{S},0,0)\equiv (\tilde{S},0,0)$ we can obtain

$$\begin{aligned} A= \begin{pmatrix} 0 &{}\quad -\frac{1}{\gamma }f_{u}(\tilde{S}) &{}\quad -\frac{\delta }{\gamma }f_{w}(\tilde{S})\\ 0 &{}\quad f_{u}(\tilde{S})-\alpha &{}\quad \beta \delta \\ 0 &{}\quad \alpha \delta ^{-1} &{}\quad f_{w}(\tilde{S})-\beta \end{pmatrix} \end{aligned}$$

(5.6)

To prove the local stability of the extinction fixed point $(\tilde{S},0,0)$, we need to show that the spectral radius of $D_{x_{0}}P(\tilde{S},0,0)$ is less than 1. From Eq. (3.4),we have

$$\begin{aligned} D_{x_{0}}P(\tilde{S},0,0)= \begin{pmatrix} \eta &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \eta &{}\quad 0\\ 0 &{}\quad 0 &{}\quad \theta _{w} \end{pmatrix} V(T) \end{aligned}$$

(5.7)

From (5.6), the eigenvalues of the matrix A are $0, \lambda _1$, and $\lambda _2$ . Here $\lambda _1,\lambda _2$ are the eigenvalues of $2\times 2$ matrix $A_1$ given by

$$\begin{aligned} A_1= \begin{pmatrix} f_{u}(\tilde{S})-\alpha &{}\quad \beta \delta \\ \alpha \delta ^{-1} &{}\quad f_{w}(\tilde{S})-\beta \end{pmatrix} \end{aligned}$$

(5.8)

Then $\lambda _1,\lambda _2$ are the roots of characteristic polynomial of $A_1$

$$\begin{aligned} g({\lambda })={\lambda }^2-[(f_{u}(\tilde{S})-\alpha ) +(f_{w}(\tilde{S})-\beta )]{\lambda }+(f_{u}(\tilde{S}) -\alpha )(f_{w}(\tilde{S})-\beta )-\alpha \beta \end{aligned}$$

The discriminant $\vartheta$ of $g({\lambda })$ is

$$\begin{aligned} \vartheta =[(f_{u}(\tilde{S})-\alpha )-(f_{w}(\tilde{S})-\beta )]^2 +4\alpha \beta >0 \end{aligned}$$

(5.9)

Thus $\lambda _1,\lambda _2$ are real value and given by

$$\begin{aligned} {\lambda }_{1,2}=\frac{[(f_{u}(\tilde{S})-\alpha ) +(f_{w}(\tilde{S})-\beta )]\pm \sqrt{\vartheta }}{2} \end{aligned}$$

(5.10)

To evaluate the spectral radius $r(D_{x_0}P(\tilde{S},0,0))$ from (5.7), we need to compute the matrix $V(t)=[V_1(t)\,\,\,V_2(t)\,\,\,V_3(t)]$.Then the dynamics of the matrix is described by

$$\begin{aligned} \frac{dV_i}{dt}&=AV_i,\quad i=1,2,3 \nonumber \\ V_i(0)&=e_i \end{aligned}$$

(5.11)

where $e_i$ are the basis vectors given by

$$\begin{aligned} e_1= \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}\!,\quad e_2= \begin{pmatrix} 0 \\ 1\\ 0 \end{pmatrix}\!,\quad e_3= \begin{pmatrix} 0 \\ 0\\ 1 \end{pmatrix} \end{aligned}$$

It is easy to show that V(t) take the following form

$$\begin{aligned} V(t)= \begin{pmatrix} 1 &{}\quad \alpha _2(t) &{}\quad \alpha _3(t) \\ 0 &{}\quad V_{11}(t) &{}\quad V_{12}(t) \\ 0 &{}\quad V_{21}(t) &{}\quad V_{22}(t) \end{pmatrix} \quad with\quad \hat{V}(t)= \begin{pmatrix} V_{11}(t) &{}\quad V_{12}(t) \\ V_{21}(t) &{}\quad V_{22}(t) \end{pmatrix} \end{aligned}$$

(5.12)

Then

$$\begin{aligned} D_{x_{0}}P(\tilde{S},0,0)= \begin{pmatrix} \eta &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \eta &{}\quad 0\\ 0 &{}\quad 0 &{}\quad \theta _{w} \end{pmatrix} V(T)= \begin{pmatrix} \eta &{}\quad \eta \alpha _2(T) &{}\quad \eta \alpha _3(T) \\ 0 &{}\quad \eta V_{11}(T) &{}\quad \eta V_{12}(T) \\ 0 &{}\quad \theta _{w}V_{21}(T) &{}\quad \theta _{w}V_{22}(T) \end{pmatrix} \end{aligned}$$

(5.13)

Note that from Eqs. (5.11) and (5.12), the matrix $\hat{V}(t)$ satisfies

$$\begin{aligned} \frac{d}{dt}\hat{V}(t)=A_1\hat{V}(t),\quad \hat{V}(0)=I \end{aligned}$$

(5.14)

Let

$$\begin{aligned} B= \begin{bmatrix} \eta V_{11}(T)&\quad \eta V_{12}(T) \\ \theta _{w}V_{21}(T)&\quad \theta _{w}V_{22}(T) \end{bmatrix} \end{aligned}$$

(5.15)

The matrix B have eigenvalues $\mu _1,\mu _2$.

Then the eigenvalues of $D_{x_{0}}P(\tilde{S},0,0)$ are $\eta$, $\mu _1$ and $\mu _2$. Since $0<\eta <1$, the spectral radius $r(D_{x_{0}}P(\tilde{S},0,0))<1$ if and only if $|\mu _i|<1,\,\,i=1,2$.

From (Allen 2007) $|\mu _i|<1,\,\,i=1,2$ if and only if

$$\begin{aligned} |det B|<1,\quad |trace B|<1+det B \end{aligned}$$

(5.16)

From (5.10) (5.14) and (5.15) and Liouvilles’ formula (Hsu 2013; Hale 1969), we can calculate the determinant det B as

$$\begin{aligned} det B&=\eta \theta _{w} det \begin{bmatrix} V_{11}(T)&\quad V_{12}(T) \nonumber \\ V_{21}(T)&\quad V_{22}(T) \end{bmatrix} \nonumber \\&=\eta \theta _{w}exp\left( \int _{0}^{T}[(f_{u}(\tilde{S})-\alpha ) +(f_{w}(\tilde{S})-\beta )]dt\right) \nonumber \\&=\eta \theta _{w}exp(({\lambda }_1+{\lambda }_2)T)\nonumber \\&=\eta \theta _{w}e^{{\lambda }_1 T}e^{{\lambda }_2T} \end{aligned}$$

(5.17)

To evaluate trace(B), we need compute $V_{11}(T)$ and $V_{22}(T)$. Let $\tilde{V}_i$ be an eigenvector of the eigenvalue $\lambda _i$ of matrix $A_1$, $i=1,2$.

It is easy to show that

$$\begin{aligned} \tilde{V}_1= \begin{pmatrix} {\lambda }_1-(f_{w}(\tilde{S})-\beta ) \\ \alpha \delta ^{-1} \\ \end{pmatrix}\quad and\quad \tilde{V}_2= \begin{pmatrix} \beta \delta \\ {\lambda }_2-(f_{u}(\tilde{S})-\alpha ) \\ \end{pmatrix} \end{aligned}$$

(5.18)

are eigenvectors of ${\lambda }_1$ and ${\lambda }_2$ respectively.

Since ${\lambda }_1\ne {\lambda }_2$ then from theory of linear system (Hsu 2013; Hale 1969),

$$\begin{aligned} \hat{V}_2(t)= & {} \begin{pmatrix} V_{11}(t) \\ V_{21}(t) \\ \end{pmatrix} =\xi _1e^{{\lambda }_1 t}\tilde{V}_1+\xi _2e^{{\lambda }_2 t}\tilde{V}_2 \nonumber \\ \hat{V}_3(t)= & {} \begin{pmatrix} V_{12}(t) \\ V_{22}(t) \\ \end{pmatrix} =\delta _1e^{{\lambda }_1 t}\tilde{V}_1+\delta _2e^{{\lambda }_2 t}\tilde{V}_2 \end{aligned}$$

(5.19)

From (5.18) and (5.19),

$$\begin{aligned} \hat{V}_2(0)= \begin{pmatrix} 1 \\ 0 \\ \end{pmatrix}\!,\quad \hat{V}_3(0)= \begin{pmatrix} 0 \\ 1 \\ \end{pmatrix} \end{aligned}$$

we obtain

$$\begin{aligned} \xi _1&=\frac{{\lambda }_2-(f_{u}(\tilde{S})-\alpha )}{({\lambda }_1-(f_{w}(\tilde{S})-\beta ))({\lambda }_2-(f_{u}(\tilde{S})-\alpha )) -\alpha \beta }\nonumber \\ \xi _2&=\frac{-(\alpha \delta ^{-1})}{({\lambda }_1-(f_{w}(\tilde{S})-\beta )) ({\lambda }_2-(f_{u}(\tilde{S})-\alpha ))-\alpha \beta } \nonumber \\ \delta _1&=\frac{\beta \delta }{({\lambda }_1-(f_{w}(\tilde{S})-\beta )) ({\lambda }_2-(f_{u}(\tilde{S})-\alpha ))-\alpha \beta } \nonumber \\ \delta _2&=\frac{{\lambda }_1-(f_{w}(\tilde{S})-\beta )}{({\lambda }_1-(f_{w}(\tilde{S})-\beta ))({\lambda }_2 -(f_{u}(\tilde{S})-\alpha ))-\alpha \beta } \end{aligned}$$

(5.20)

From (5.10), we note that

$$\begin{aligned} {\lambda }_1+{\lambda }_2=(f_{u}(\tilde{S})-\alpha )+(f_{w}(\tilde{S})-\beta ) \end{aligned}$$

or

$$\begin{aligned} ({\lambda }_1-(f_{w}(\tilde{S})-\beta ))=-({\lambda }_2-(f_{u}(\tilde{S})-\alpha )) \end{aligned}$$

(5.21)

From (5.18),(5.19), (5.20), and (5.21), we can obtain

$$\begin{aligned} V_{11}(T)&=A_1e^{{\lambda }_1T}+A_2e^{{\lambda }_2T} \\ V_{22}(T)&=A_2e^{{\lambda }_1T}+A_1e^{{\lambda }_2T} \end{aligned}$$

where

$$\begin{aligned} A_1= & {} \frac{-({\lambda }_1-(f_{w}(\tilde{S})-\beta )) ({\lambda }_2-(f_{u}(\tilde{S})-\alpha ))}{\alpha \beta -({\lambda }_1-(f_{w}(\tilde{S})-\beta ))({\lambda }_2 -(f_{u}(\tilde{S})-\alpha ))} \nonumber \\ A_2= & {} \frac{\alpha \beta }{\alpha \beta -({\lambda }_1-(f_{w}(\tilde{S}) -\beta ))({\lambda }_2-(f_{u}(\tilde{S})-\alpha ))}\nonumber \\ 0\le & {} A_1,\quad A_2 \le 1,\quad A_1+A_2=1 \end{aligned}$$

(5.22)

Using (5.16), the stability condition for the extinction fixed point $E_0=(\tilde{S},0,0)$ is given by

$$\begin{aligned} \eta \theta _{w}e^{{\lambda }_1T}e^{{\lambda }_2T}< & {} 1 \end{aligned}$$

(5.23)

$$\begin{aligned} \eta V_{11}(T)+\theta _{w}V_{22}(T)< & {} 1+\eta \theta _{w} e^{{\lambda }_1T}e^{{\lambda }_2T} \end{aligned}$$

(5.24)

Appendix B: Proof of Lemma A

Lemma 1

Define $(S_n,u_n,w_n)=P^n(S_0,u_0,w_0)$. For any $(S_0,u_0,w_0)\in {\mathbb {R}}^3$, the sequence ${(S_n,u_n,w_n)}^{n=\infty }_{n=0}$ is bounded.

Proof

From the first equation in (3.1), we have $S'(t)\le 0, 0<t<T$, and $S(T)\le S_0$ since $S_1=\eta S(T)+FS^{(0)}\le \eta S_0+FS^{(0)}$. Inductively we have $S_{n+1}=\eta S_n+FS^{(0)}$, n = 0,1,2......, then

$$\begin{aligned} S_{n}\le \eta S_{n-1}+FS^{(0)}&\le \eta (\eta S_{n-2}+FS^{(0)})+FS^{(0)}\le \cdots \cdots \cdots \\&\le \eta ^nS_0+FS^{(0)}(1+\eta +\cdots \cdots \cdots +\eta ^{n-1}) \end{aligned}$$

Given $\epsilon >0$ small for n large

$$\begin{aligned} S_n\le \frac{FS^{(0)}}{1-\eta }+\epsilon =S^{(0)} +\epsilon \quad for\quad n\ge N_0 \end{aligned}$$

Let $U(t)=\frac{1}{\gamma }(u(t)+\delta w(t))$ and $U_n=\frac{1}{\gamma }(u_n+\delta w_n)$, $n\ge 0$.

Then $S(t)+U(t)=S_0+U_0$ for $0\le t\le T$ and

$$\begin{aligned} U'= & {} \frac{1}{\gamma } (f_u(S)u+f_w(S)\delta w) \\\le & {} Max(f_u(S),f_w(S))U \\= & {} Max(f_u(S_0+U_0-U(t)),f_w(S_0+U_0-U(t))U \\ U(0)= & {} U_0 \end{aligned}$$

Hence $U(t)\le S_0+U_0$, $0\le t\le T$.

Let $\theta ^*=max\{\eta ,\theta _w\}$, then

$$\begin{aligned} U_1=\frac{1}{\gamma }(u_1(T^{-})+\delta w_1(T^{-})) \le \theta ^*U(T^{-})\le \theta ^*(S_0+U_0)\le \theta ^*((S^{(0)}+\epsilon )+U_0) \end{aligned}$$

Inductively for $n\ge 1$, we have

$$\begin{aligned} U_n\le & {} \theta ^*((S^{(0)}+\epsilon )+U_{n-1}) \\\le & {} \theta ^*((S^{(0)}+\epsilon ) +\theta ^*((S^{(0)}+\epsilon )+U_{n-2}) \\&............................\\\le & {} \theta ^*((S^{(0)}+\epsilon )(1+\theta ^*+\cdots \cdots \cdots \cdots (\theta ^*)^{n-1})+(\theta ^*)^nU_{0}) \end{aligned}$$

For large n, we have

$$\begin{aligned} U_n\le \frac{\theta ^*(S^{(0)}+\epsilon )}{1-\theta ^*} +\epsilon _1,\quad \epsilon ,\epsilon _1\quad are\quad small. \end{aligned}$$

Hence ${(S_n,u_n,w_n)}^{n=\infty }_{n=0}$ are bounded.

Proof of Theorem A, part(i)

Consider the following auxiliary system of (3.1)

$$\begin{aligned} S'&=0 \nonumber \\ u'&=(f_u(S)-\alpha )u+\beta \delta w \nonumber \\ w'&=(f_w(S)-\beta )w+\alpha \delta ^{-1} u \end{aligned}$$

(5.25)

$S(0)=S_0,\,\,u(0)=u_0,\,\,w(0)=w_0$ with with the same resetting of initial condition (3.1) at $t=T^{+}$.

Define map $\hat{P}(\hat{S}_0,\hat{u}_0,\hat{w}_0)=L \circ \psi _{T}(\hat{S}_0,\hat{u}_0,\hat{w}_0)$, with $(\hat{S}_0,\hat{u}_0,\hat{w}_0)=(S_{0},u_{0},w_{0})$, L defined in (4.3) and $\psi _t(\hat{x}_0)$ is the semi-flow defined by the system Eq. (5.25), $0\le t\le T$, $\hat{x}_0=(\hat{S}_0,\hat{u}_0,\hat{w}_0)$. We write initial value problem (5.25) in vector form

$$\begin{aligned} \frac{dX}{dt}&=\hat{F}(X) \nonumber \\ X(0)&=\hat{x}_0 \end{aligned}$$

(5.26)

Then $F(X)\le \hat{F}(X)$. We note that (5.3) is a cooperationsystem for $0\le t\le T$.

Let $(\hat{S}_n,\hat{u}_n,\hat{w}_n)=\hat{P}^n (\hat{S}_0,\hat{u}_0,\hat{w}_0)$.

By Kamke theorem (Smith 1995) and the resetting mechanism (3.1), it follows that

$$\begin{aligned} (S_n,u_n,w_n)\le (\hat{S}_n,\hat{u}_n,\hat{w}_n)\quad for \quad all \quad n\ge 0. \end{aligned}$$

We want to show that if (3.6) holds, i.e., the extinction state $(S^{(0)},0,0)$ is locally stable for the map P, then $(\hat{u}_n,\hat{w}_n)\rightarrow (0,0)$ as $n\rightarrow \infty$.

From the proof of Lemma A1, it follows that

$$\begin{aligned} \hat{S_n}=\eta ^n S_0+FS^{(0)}(1+\eta +\cdots \cdots \cdots +\eta ^{n-1})\rightarrow S^{(0)}\quad as \quad n\rightarrow \infty . \end{aligned}$$

For $\epsilon >0$ small,

$$\begin{aligned} S^{(0)}-\epsilon <S_n<S^{(0)}+\epsilon \quad for\quad n\ge N \end{aligned}$$

Let

$$\begin{aligned} \hat{F}^{\pm }(S,u,w)= \begin{pmatrix} (f_{u}(S^{(0)}\pm \epsilon )-\alpha )u+\beta \delta w \\ (f_{w}(S^{(0)}\pm \epsilon )-\beta )w+\alpha \delta ^{-1}u \\ \end{pmatrix} \end{aligned}$$

Then

$$\begin{aligned} \hat{F}^{-}(S,u,w)<\hat{F}(S,u,w)<\hat{F}^{+}(S,u,w) \end{aligned}$$

By Kamke’s Theorem and resetting mechanism, it follows that

$$\begin{aligned} (S^{(0)}-\epsilon ,u^{-}_n,w^{-}_n)<(S_n,u_n,w_n) <(S^{(0)}+\epsilon ,u^{+}_n,w^{+}_n) \end{aligned}$$

Since $r(D_{x_0}\hat{P}(S^{(0)},0,0))=r(D_{x_0}P(S^{(0)},0,0))$, then $r(D_{x_0}\hat{P}(S^{(0)},0,0))<1$ implies $r(D_{x_0} \hat{P}^{\pm }(S^{(0)} \pm \epsilon ,0,0) <1$ for $\epsilon >0$, $(u^{\pm }_n,w^{\pm }_n)\rightarrow (0,0)$ as $n\rightarrow \infty$. Hence if the stability condition (3.6) holds then $(u_n,w_n)\rightarrow (0,0)$ as $n\rightarrow \infty$.

Proof of Theorem A, part(ii)

We shall prove uniformly persistence of the map P if $r(D_{x_0}P(S^{(0)},0,0))>1$ i.e., Eq. (3.6) does not hold with strict inequality. Since $E_0=(S^{(0)},0,0)$ is the only fixed point on the boundary of $Int({\mathbb {R}}^3_{+})$, from Theorem 1.3.1 (Zhao 2003; Freedman and So 1989) and Lemma A1, it suffices to show that

$$\begin{aligned} W^s(E_0)\cap Int({\mathbb {R}}^3_{+})=\emptyset , \end{aligned}$$

where $W^s(E_0)=\{x_0\in {\mathbb {R}}^3_{+}:P^n(x_0)\rightarrow E_0\,\,\,as\,\,\,n\rightarrow \infty \}$ is the stable set of fixed point $E_0$.

We prove by contradiction. If this is not the case, there exists $x_0=(S_0,u_0,w_0)\in Int({\mathbb {R}}^3_{+})$ such that $P^n(x_0)\rightarrow E_0$ as $n\rightarrow \infty$.

Then we have $S_n\rightarrow \tilde{S},\,\,u_n\rightarrow 0\,\,w_n\rightarrow 0$ as $n\rightarrow \infty$. From Eqs. (5.1) and (5.2) and stability condition $r(D_{x_0}P(S^{(0)},0,0))>1$ , it follows that $(u^{-}_n,w^{-}_n)\rightarrow \infty$ as $n\rightarrow \infty$, a contradiction. From Theorem 1.3.7 (Zhao 2003), there exists a positive fixed point $E=(S^*,u^*,w^*)$ of the map P.

Proof of Theorem B

First we claim that under the assumptions (3.15) and (3.16) we have

$$\begin{aligned} \gamma S_n+u_n+\delta w_n\rightarrow \gamma S^{(0)}\quad as\quad n\rightarrow \infty . \end{aligned}$$

(5.27)

From (2.1) it follows that

$$\begin{aligned} \gamma S(t)+u(t)+\delta w(t)=K_n=\gamma S_n+u_n+\delta w_n\quad for\quad nT\le t\le (n+1)T \end{aligned}$$

By the assumption (3.15) we have

$$\begin{aligned} \gamma S_{n+1}+u_{n+1}+\delta w_{n+1}&=\gamma S(T_{n+1}^+)+u(T_{n+1}^+)+\delta w(T_{n+1}^+) \nonumber \\&=\gamma (\eta S_n+(1-\eta )S^{(0)})+\eta u_n+\theta _w\delta w_n \nonumber \\&=\eta (\gamma S_n+u_n+\delta w_n)+\gamma (1-\eta )S^{(0)} \end{aligned}$$

(5.28)

From above the set $W=\{(S, u, w):\gamma S+u+\delta w=\gamma S^{(0)}\}$ is positively invariant under the map P. Furthermore, from (5.28) inductively we have

$$\begin{aligned}&\gamma S_n+u_n+\delta w_n=\eta ^n(\gamma S_0+u_0+\delta w_0)+\gamma (1-\eta )S^{(0)}(1+\eta +\cdots \\&\qquad +\,\eta ^{n-1})\rightarrow \gamma S^{(0)}\\&\quad as\quad n\rightarrow \infty . \end{aligned}$$

Let $U=u+\delta w$. Under the assumption (3.16) we have

$$\begin{aligned} \frac{dU}{dt}&=f(S)U \\ U(T_n^+)&=\eta U(T_n^-). \end{aligned}$$

From (5.27) we consider the following limiting system

$$\begin{aligned} \frac{dU}{dt}&=f(S^{(0)}-\frac{1}{\gamma }U)U \nonumber \\ U(T_n^+)&=\eta U(T_n^-). \end{aligned}$$

(5.29)

from [4] let $R_1=\frac{f(S^{(0)})T}{ln(\frac{1}{\eta })}$, it follows that if $R_1<1$, then $U(T_n^+)\rightarrow 0$; if $R_1>1$, then there exists a unique fixed point $\hat{U}$ of the system (5.29) such that

$$\begin{aligned} U(T_n^+)\rightarrow \hat{U}\quad as\quad n \rightarrow \infty \quad for\quad any\quad initial\quad condition\quad U_0>0. \end{aligned}$$

For the case $R_1>1$ equivalently $\eta >\eta ^*=e^{-f(S^{(0)})T}$, we consider the limiting equation of the second equation of (2.1)

$$\begin{aligned} \frac{du}{dt}&=\left( f\left( S^{(0)}-\frac{1}{\gamma }\hat{U}\right) -\alpha \right) u+\beta (\hat{U}-u) \\ u(T_n^+)&=\eta u(T_n^-). \end{aligned}$$

The above equation can be written as

$$\begin{aligned} \frac{du}{dt}&=\left( f\left( S^{(0)}-\frac{1}{\gamma }\hat{U}\right) -(\alpha +\beta )\right) u+\beta \hat{U} \\&:=Au+B. \end{aligned}$$

It is easy to show that

$$\begin{aligned} \frac{du}{dt}&=\left( f\left( S^{(0)}-\frac{1}{\gamma }\hat{U}\right) -(\alpha +\beta )\right) u+\beta \hat{U} \\&:=Au+B. \end{aligned}$$

Since $\eta >e^{-f(S^{(0)})T}$, it is easy to check that $\eta e^{AT}<1$ holds.

Hence

$$\begin{aligned} u_n=u(T_n^+)&\rightarrow \hat{u}=\frac{B}{A}\eta (e^{AT}-1) \frac{1}{1-de^{AT}}\\ and\\ (S_n, u_n, \delta w_n)&\rightarrow (S^{(0)}-\hat{U}, \hat{u}, \hat{U}-\hat{u}) \quad as\quad n\rightarrow \infty . \end{aligned}$$

We note that from chapter 1 (Zhao 2003) it is easy to lift the limiting systems (5.29) and (A.30) to the original system (2.1). Thus we complete the proof.