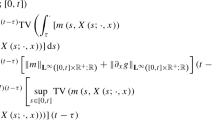Abstract
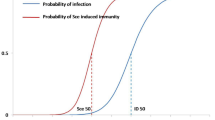
When the body gets infected by a pathogen the immune system develops pathogen-specific immunity. Induced immunity decays in time and years after recovery the host might become susceptible again. Exposure to the pathogen in the environment boosts the immune system thus prolonging the time in which a recovered individual is immune. Such an interplay of within host processes and population dynamics poses significant challenges in rigorous mathematical modeling of immuno-epidemiology. We propose a framework to model SIRS dynamics, monitoring the immune status of individuals and including both waning immunity and immune system boosting. Our model is formulated as a system of two ordinary differential equations (ODEs) coupled with a PDE. After showing existence and uniqueness of a classical solution, we investigate the local and the global asymptotic stability of the unique disease-free stationary solution. Under particular assumptions on the general model, we can recover known examples such as large systems of ODEs for SIRWS dynamics, as well as SIRS with constant delay.




Similar content being viewed by others
References
Amanna IJ, Carlson NE, Slifka MK (2007) Duration of humoral immunity to common viral and vaccine antigens. New Eng J Med 357(19):1903–1915
Antia R, Ganusov VV, Ahmed R (2005) The role of models in understanding CD8+ T-cell memory. Nat Rev Immunol 5(2):101–111
Arinaminpathy N, Lavine JS, Grenfell BT (2012) Self-boosting vaccines and their implications for herd immunity. Proc Natl Acad Sci USA Early Ed 109(49):154–159
Arino J, van den Driessche P (2006) Time delays in epidemic models. In: Delay differential equations and applications, NATO Science Series, vol 205. Springer, New York, pp 539–578
Aron JL (1983) Dynamics of acquired immunity boosted by exposure to infection. Math Biosci 64(2):249–259
Aron JL (1988) Acquired immunity dependent upon exposure in an SIRS epidemic model. Math Biosci 88(1):37–47
Aron JL (1988) Mathematical modelling of immunity to malaria. Math Biosci 90(1–2):385–396
Bhattacharya S, Adler FR (2012) A time since recovery model with varying rates of loss of immunity. Bull Math Biol 74(12):2810–2819
Blyuss KB, Kyrychko YN (2010) Stability and bifurcations in an epidemic model with varying immunity period. Bull Math Biol 72(2):490–505
Breda D, Diekmann O, De Graaf WF, Pugliese A, Vermiglio R (2012) On the formulation of epidemic models (an appraisal of Kermack and McKendrick). J Biol Dyn 6(Suppl2):103–117
Calsina À, Saldaña J (1995) A model of physiologically structured population dynamics with a nonlinear individual growth rate. J Math Biol 33(4):335–364
Calsina À, Farkas JZ (2012) Steady states in a structured epidemic model with Wentzell boundary condition. J Evol Equ 12(3):495–512
Dafilis MP, Frascoli F, Wood JG, McCaw JM (2012) The influence of increasing life expectancy on the dynamics of SIRS systems with immune boosting. ANZIAM J 54(1–2):50–63
De Graaf WF, Kretzschmar MEE, Teunis PFM, Diekmann O (2014) A two-phase within-host model for immune response and its application to serological profiles of pertussis. Epidemics 9:1–7
Ellner SP (2009) Lectures on theoretical ecology. Cornell University, New York
Gandolfi A, Pugliese A, Sinisgalli C (2015) Antibody dynamics in childhood diseases: waning and boosting of immunity and the impact of vaccination. J Math Biol 70(3):399–435
Glass K, Grenfell BT (2003) Antibody dynamics in childhood diseases: waning and boosting of immunity and the impact of vaccination. J Theor Biol 221(1):121–131
Goldsby RA, Kindt TJ, Osborne BA, Kubi J (2003) Immunology, 5th edn. W. H. Freeman and Company, London
Heffernan JM, Keeling MJ (2008) An in-host model of acute infection: measles as a case study. Theor Popul Biol 73(1):134–147
Heffernan JM, Keeling MJ (2009) Implications of vaccination and waning immunity. Proc R Soc B Biol Sci 276(1664):2071–2080
Kyrychko YN, Blyuss KB (2005) Global properties of a delayed SIR model with temporary immunity and nonlinear incidence rate. Nonlinear Anal Real 6(3):495–507
Lavine JS, King AA, Bjørnstad ON (2011) Natural immune boosting in pertussis dynamics and the potential for long-term vaccine failure. Proc Nat Acad Sci 108(17):7259–7264
Li S, Rouphael N, Duraisingham S et al (2013) Molecular signatures of antibody responses derived from a systems biology study of five human vaccines. Nat Immunol 15(2):195–204
Luo Z, Shi H, Zhang H et al (2012) Plasmid DNA containing multiple CpG motifs triggers a strong immune response to hepatitis B surface antigen when combined with incomplete Freund’s adjuvant but not aluminum hydroxide. Mol Med Rep 6:1309–1314
Martcheva M, Pilyugin SS (2006) An epidemic model structured by host immunity. J Biol Sys 14(02):185–203
McLean AR, Anderson RM (1988a) Measles in developing countries. Part II. The predicted impact of mass vaccination. Epidemiol Inf 100(3):419–442
McLean AR, Anderson RM (1988b) Measles in developing countries. Part I. Epidemiological parameters and patterns. Epidemiol Inf 100(1):111–133
Metz JA, Diekmann O (1986) The dynamics of physiologically structured populations, lecture notes in biomathematics, vol 68. Springer, New York
Moghadas SM, Alexander ME, Sahai BM (2008) Waning herd immunity: a challenge for eradication of measles. Rocky Mt J Math 38(5):1587–1607
Mossong J, Nokes DJ et al (1999) Modeling the impact of subclinical measles transmission in vaccinated populations with waning immunity. Am J Epidemiol 150(11):1238–1249
Mossong J, Muller CP (2003) Modelling measles re-emergence as a result of waning of immunity in vaccinated populations. Vaccine 21(31):4597–4603
Pazy A (1983) Semigroups of linear operators and applications to partial differential equations. Springer, New York
Rouderfer V, Becker NG, Hethcote HW (1994) Waning immunity and its effects on vaccination schedules. Math Biosci 124(1):59–82
Schiesser WE (1991) The numerical method of lines. Academic Press, San Diego
Siegrist CA (2008) Vaccine immunology. In: Plotkin SA, Orenstein WA, Offit PA (eds) Vaccines. Elsevier Inc, Philadelphia, pp 17–36
Taylor ML, Carr TW (2009) An SIR epidemic model with partial temporary immunity modeled with delay. J Math Biol 59(6):841–880
Webb GF (2008) Population models structured by age, size, and spatial position. In: Magal P, Auger P (eds) Structured population models in biology and epidemiology. Springer, Heidelberg, pp 1–49
White LJ, Medley GF (1998) Microparasite population dynamics and continuous immunity. Proc R Soc Lond B Biol 265(1409):1977–1983
Wodarz D (2007) Killer cell dynamics: mathematical and computational approaches to immunology. Springer, New York
Yuan Y, Bélair J (2013) Threshold dynamics in an SEIRS model with latency and temporary immunity. J Math Biol 69(4):875–904
Acknowledgments
MVB was supported by the ERC Starting Grant No. 259559 as well as by the European Union and the State of Hungary, co-financed by the European Social Fund in the framework of TÁMOP-4.2.4. A/2-11-1-2012-0001 National Excellence Program. GR was supported by Hungarian Scientific Research Fund OTKA K109782 and TÁMOP-4.2.2.A-11/1/KONV-2012-0073 “Telemedicine focused research activities on the field of Mathematics, Informatics and Medical sciences”.
Author information
Authors and Affiliations
Corresponding author
Proof of Theorem 1
Proof of Theorem 1
In the following we show the continuous differentiability of the map \(Q\), which is necessary to have existence and uniqueness of a classical solution of the abstract Cauchy problem (8). Continuous differentiability of \(Q\) can be shown in two steps: (a) First we determine the existence of the operator \(DQ(x;w)\), for all \(x,\,w \in X\), defined by
(b) Second we show that the operator \(DQ(x;\cdot )\) is continuous in \(x\), that is
where \(\Vert \cdot \Vert _{OP}\) is the operator norm.
For simplicity of notation we write
where
Proof of (a)
We compute the limit for the first component of \(Q_1\),
For the second term in \(Q_1(x)\) we have
The first term in \(Q_3(x)\):
Hence we have
Analogously, compute the last term in \(Q_3(x)\),
To prove that the operator \(DQ(x;\cdot )\) is continuous in \(x\) we consider the norm \(\Vert DQ(x;\cdot ) -DQ(y;\cdot ) \Vert _{OP}\), that is
and show that
We estimate the operator norm as follows
with
Then we show the convergence to zero of the above sum. It is obvious that
as \(b\) is continuously differentiable (see Assumption 1),
The term in \(T_2(x,y;w)\) can be estimated as follows:
Since the addends of the last sum are all similar, we show convergence to zero for only one of them.
It works analogously for the terms \(L_1(x,y;w)\) and \(L_2(x,y;w)\). Hence we have that
In a similar way one can estimate \(T_3(x,y;w)\) and \(T_4(x,y;w)\). We show the computation for \(T_4\) which is the most challenging of the two, as it includes double integrals.
Before proceeding to the next estimate, it is useful to observe that
Let us now consider the last addend in \(T_4(x,y;w)\). We have that
A similar computation as the one for \(\underset{ \left\| {w}\right\| _X\le 1 }{\sup }\;L_3(x,y;w)\) yields
Similar relations hold for the other terms \(F_1(x,y;w)\), \(F_2(x,y;w)\) and \(F_3(x,y;w)\). It is then obvious that the norm \( \Vert DQ(x;\cdot ) -DQ(y;\cdot ) \Vert _{OP}\) tends to zero, for \(\left\| {x- y}\right\| _X\) going to zero, and the proof is complete. \(\square \)
Rights and permissions
About this article
Cite this article
Barbarossa, M.V., Röst, G. Immuno-epidemiology of a population structured by immune status: a mathematical study of waning immunity and immune system boosting. J. Math. Biol. 71, 1737–1770 (2015). https://doi.org/10.1007/s00285-015-0880-5
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00285-015-0880-5
Keywords
- Immuno-epidemiology
- Waning immunity
- Immune status
- Boosting
- Physiological structure
- Reinfection
- Delay equations
- Global stability
- Abstract Cauchy problem