On the uniqueness of epidemic models fitting a normalized curve of removed individuals

Abstract

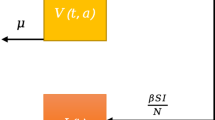
The susceptible-infected-removed (SIR) and the susceptible-exposed-infected-removed (SEIR) epidemic models with constant parameters are adequate for describing the time evolution of seasonal diseases for which available data usually consist of fatality reports. The problems associated with the determination of system parameters starts with the inference of the number of removed individuals from fatality data, because the infection to death period may depend on health care factors. Then, one encounters numerical sensitivity problems for the determination of the system parameters from a correct but noisy representative of the number of removed individuals. Finally as the available data is necessarily a normalized one, the models fitting this data may not be unique. We prove that the parameters of the (SEIR) model cannot be determined from the knowledge of a normalized curve of “Removed” individuals and we show that the proportion of removed individuals, $R(t)$, is invariant under the interchange of the incubation and infection periods and corresponding scalings of the contact rate. On the other hand we prove that the SIR model fitting a normalized curve of removed individuals is unique and we give an implicit relation for the system parameters in terms of the values of $R_m/R_f$ and $R^{\prime }_m/R_f$, where $R_f$ is the steady state value of $R(t)$ and $R_m$ and $R^{\prime }_m$ are the values of $R(t)$ and its derivative at the inflection point $t_m$ of $R(t)$. We use these implicit relations to provide a robust method for the estimation of the system parameters and we apply this procedure to the fatality data for the H1N1 epidemic in the Czech Republic during 2009. We finally discuss the inference of the number of removed individuals from observational data, using a clinical survey conducted at major hospitals in Istanbul, Turkey, during 2009 H1N1 epidemic.

Appendix A

We use Istanbul data to develop a statistical method for shifting the observed date of fatality back or forth in order to infer a correct representative of $R(t)$. The first step is to show that the time-to-death distribution is nearly log-normal (Crow and Shimizu 1988). To proceed further, one has to start with an a priori estimate of the mean and the standard deviation of the logarithm of the time-to-death intervals. The next step is to partition the time axis into a reasonable number of bins bounded by $0<ln(t_1)<\cdots <ln(t_n)<\infty$. The proportion of the cases with a duration belonging to a bin $[t_{i-1},t_i]$, denoted by $p_i$ can be computed from the log-normal distribution. We then translate the time axis for the occurrence of fatalities to the day of the first fatality and compute the proportion $q_i$ of the fatalities that occur in the bin $[t_{i-1},t_i]$. By a simple pigeon hole principle, all fatality cases with duration belonging to the last bin, should have been occurred at the last bin. By similar arguments that will be illustrated below, we obtain a system of under-determined equations with inequality constraints, that we solve as an optimization problem, to determine the proportion $\alpha _{i,j}$ of fatalities that occur in bin $i$ to have duration belonging to the bin $j$. The final step is to move the cases in the bin $i$ back or forth according to the parameters $\alpha _{i,j}$. We note that this process aims only to correct for excessively long hospitalization periods.

Working with Istanbul data, in Fig. 12a, b, we present the histograms for the time-to-death durations with respect to time and with respect to the logarithm of time, measured in days. The first figure seems to have an exponential decay, while the second one is centered in the 7–12 day interval. The mean, standard deviation and higher central moments are computed as

$$\begin{aligned} \mu =2.4953,\quad \sigma =0.9465,\quad \mathrm{Skewness}=0.0269,\quad \mathrm{Kurtosis}=3.2188. \end{aligned}$$

The Jarque–Bera test statistic with 0.05 confidence interval (with value $JB=0.093$) allows us to consider the time-to-death duration as log-normal distributed.

Fig. 12

The histogram of the time-to-death intervals with respect to days (a). The histogram of the time-to-death intervals with respect to the logarithm of days. The distribution is approximately normal, centered at $\mu =2.49$ (7–12 days), with standard deviation $\sigma =0.94$, skewness 0.026 and kurtosis 3.21 (b)

We divide the logarithmic time scale into 6 bins separated by

$$\begin{aligned}&\displaystyle ln(t): -\infty <0<1<2<3<4<5, \\&\displaystyle t: 0<1.0000< 2.7183 < 7.3891< 20.0855< 54.5982 <148.4132. \end{aligned}$$

The probabilities $p_i$ that the duration of time-to-death falls in these bins are computed from the log-normal distribution with parameters above as

$$\begin{aligned} p_1&= 0.0042,\quad p_2=0.0529,\quad p_3=0.2433,\quad p_4=0.4027,\nonumber \\ p_5&= 0.2410,\quad p_6= 0.0559. \end{aligned}$$

The proportion $q_i$ of deaths that occur in these bins is an observable quantity. In the case of Istanbul data these are observed as

$$\begin{aligned} q_1=1/46,\quad q_2=2/46,\quad q_3=4/46,\quad q_4=24/46,\quad q_5=12/46,\quad q_6=3/46. \end{aligned}$$

As above, let $\alpha _{i,j}$ be the contribution of cases with duration in the $j$th bin to fatalities occurring in the $i$th bin. Clearly, longer durations cannot contribute to earlier fatalities. Thus $\alpha _{i,j}=0$ for $i<j$. If the number of bins is $n$, the number of parameters is $n(n+1)/2$ subject to the constraints $0<\alpha _{i,j}<1$ and $\sum _j \alpha _{i,j}=1$. With the bin selection as above, we aim to approximate the $q_i$’s by the expressions at the right hand sides of the system below.

$$\begin{aligned} q_1&\sim \alpha _{1,1}p_1, \\ q_2&\sim \alpha _{2,1}p_1+\alpha _{2,2}p_2, \\ q_3&\sim \alpha _{3,1}p_1+\alpha _{3,2}p_2+\alpha _{3,3}p_3, \\ q_4&\sim \alpha _{4,1}p_1+\alpha _{4,2}p_2+\alpha _{4,3}p_3+\alpha _{4,4}p_4, \\ q_5&\sim \alpha _{5,1}p_1+\alpha _{5,2}p_2+\alpha _{5,3}p_3+\alpha _{5,4}p_4+\alpha _{5,5}p_5, \\ q_6&\sim \alpha _{6,1}p_1+\alpha _{6,2}p_2+\alpha _{6,3}p_3+\alpha _{6,4}p_4+\alpha _{6,5}p_5+\alpha _{6,6}p_6, \end{aligned}$$

together with the constraints

$$\begin{aligned} \sum _j \alpha _{i,j}=1, \quad k_0<\alpha _{i,j}<1, \end{aligned}$$

where $k_0>0$ may be a non-zero lower bound. We search for an optimal solution minimizing the least-square error between the right and left hand sides of the expressions above, subject to the constraints. For the example under consideration, the matrices $\alpha _{i,j}$ for lower bounds $k_0=0$ and $k_0=0.1$ are given below.

$$\begin{aligned} \alpha _{i,j}{(0)}=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1\\ \end{array} \right) ,\quad \alpha _{i,j}{(1)}=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0.1 &{} 0.1 &{} 0.1 &{} 0.5 &{} 0.1 &{} 0.1\\ 0 &{} 0.1 &{} 0.1 &{} 0.6 &{} 0.1 &{} 0.1\\ 0 &{} 0 &{} 0.1 &{} 0.7 &{} 0.1 &{} 0.1\\ 0 &{} 0 &{} 0 &{} 0.8 &{} 0.1 &{} 0.1\\ 0 &{} 0 &{} 0 &{} 0 &{} 0.9 &{} 0.1\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ \end{array} \right) . \end{aligned}$$

We define the percentage contribution of the cases with duration in the $j$th bin, to fatalities occurring in the $i$th bin, as

$$\begin{aligned} H_{i,j}=\frac{\alpha _{i,j}}{\sum _k\alpha _{k,j}}. \end{aligned}$$

For the $\alpha _{i,j}{(1)}$ matrix this gives

$$\begin{aligned} H{i,j}{(1)}=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 1 &{} 1/2 &{} 1/3 &{} 5/26 &{} 1/13 &{} 1/15\\ 0 &{} 1/2 &{} 1/3 &{} 6/26 &{} 1/13 &{} 1/15\\ 0 &{} 0 &{} 1/3 &{} 7/26 &{} 1/13 &{} 1/15\\ 0 &{} 0 &{} 0 &{} 8/26 &{} 1/13 &{} 1/15\\ 0 &{} 0 &{} 0 &{} 0 &{} 9/13 &{} 1/15\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{}10/15 \\ \end{array} \right) . \end{aligned}$$

Note that the entries of the $H_{i,j}$ can be interpreted as conditional probabilities. We see that contributions fatalities that occur late have longer durations. In order to construct a curve that approximates more closely the time evolution of the number of removed individuals, one can shift back the proportion $H_{i,j}$ of the date of fatalities in the $i$th bin, by some value in the $j$th bin, then add the incubation period. If the incubation period is unknown, the process described above will give a time translate of the correct curve. For example, we have to move two thirds of the fatalities occurring later than the 54th day of the epidemic, by an amount between 54 and 148 days. Similarly, $9/13$th of the fatalities occurring between the 20th and 54th days of the epidemic have to be moved back.

We would like to note that the method proposed here is only a preprocessing for obtaining a better approximation to the number of removed individuals. The analysis of the previous sections have to be carried out in order to obtain the incidence curves from fatality data.