A Piecewise Deterministic Markov Toy Model for Traffic/Maintenance and Associated Hamilton–Jacobi Integrodifferential Systems on Networks

Abstract

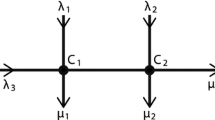
We study optimal control problems in infinite horizon whxen the dynamics belong to a specific class of piecewise deterministic Markov processes constrained to star-shaped networks (corresponding to a toy traffic model). We adapt the results in Soner (SIAM J Control Optim 24(6):1110–1122, 1986) to prove the regularity of the value function and the dynamic programming principle. Extending the networks and Krylov’s “shaking the coefficients” method, we prove that the value function can be seen as the solution to a linearized optimization problem set on a convenient set of probability measures. The approach relies entirely on viscosity arguments. As a by-product, the dual formulation guarantees that the value function is the pointwise supremum over regular subsolutions of the associated Hamilton–Jacobi integrodifferential system. This ensures that the value function satisfies Perron’s preconization for the (unique) candidate to viscosity solution.

Appendix

1.1 Proof of Lemma 6

Proof of Lemma 6

We will consider several cases and prove (i) in each case. We provide the construction for (ii) only in the first case (a) and hint what is needed for the remaining cases.      

(a) (i) Let us assume that $x=O$. If $y=O,$ then $\mathcal {P}_{O,y}\left( \alpha \right) =\alpha .$ Otherwise, we let $t_{y,O}:=\inf \left\{ t\ge 0:y_{\gamma }\left( t;y,a_{\gamma ,1}^{-}\right) =O\right\} .$ Obviously,

$$\begin{aligned} t_{y,O}\le \frac{\left| y\right| ^{1-\kappa }}{\left( 1-\kappa \right) \beta }\le \frac{\rho _{\varepsilon }^{2}}{\left( 1-\kappa \right) \beta }. \end{aligned}$$

(These estimates are for the “inactive” case; for the “active” one, one can consider $\kappa =0$). For $\varepsilon$ small enough, one can assume, without loss of generality that $\frac{\rho _{\varepsilon }}{\left( 1-\kappa \right) \beta }<t_{\varepsilon }.$ We define

$$\begin{aligned} \mathcal {P}_{O,y}\left( \alpha \right) \left( t\right) :=a_{\gamma ,1} ^{-}\mathbf {1}_{\left[ 0,t_{y,O}\right] }\left( t\right) +\alpha \left( t-t_{y,O}\right) \mathbf {1}_{(t_{y,O},\infty )}\left( t\right) , \end{aligned}$$

for all $t\ge 0.$ Then, one gets

$$\begin{aligned} \left| y_{\gamma }\left( t;y,\mathcal {P}_{O,y}\left( \alpha \right) \right) -y_{\gamma }\left( t;O,\alpha \right) \right| \!&\le \!\left| y_{\gamma }\left( t;y,\mathcal {P}_{O,y}\left( \alpha \right) \right) -y\right| +\left| y\right| +\left| y\left( t;O,\alpha \right) \right| \\&\le \left( \frac{2\left| f\right| _{0}}{\left( 1-\kappa \right) \beta }+1\right) \left| y\right| ^{1-\kappa }\le \left( \frac{2\left| f\right| _{0}}{\left( 1-\kappa \right) \beta }+1\right) \rho _{\varepsilon }^{2}, \end{aligned}$$

if $t\in \left[ 0,t_{y,O}\right]$ and

$$\begin{aligned} \left| y_{\gamma }\left( t;y,\mathcal {P}_{O,y}\left( \alpha \right) \right) -y_{\gamma }\left( t;O,\alpha \right) \right|&=\left| y_{\gamma }\left( t;O,\alpha \right) -y_{\gamma }\left( t-t_{y,O} ;O,\alpha \right) \right| \\&\le \frac{\left| f\right| _{0}}{\left( 1-\kappa \right) \beta }\left| y\right| ^{1-\kappa }\le \frac{\left| f\right| _{0} }{\left( 1-\kappa \right) \beta }\rho _{\varepsilon }^{2}, \end{aligned}$$

if $t>t_{y,O}.$ Moreover, for every $T\ge 0,$

$$\begin{aligned}&\left| \int _{0}^{T}e^{-\delta t}l_{\gamma }\left( y_{\gamma }\left( t;y,\mathcal {P}_{O,y}\left( \alpha \right) \right) ,\mathcal {P}_{O,y}\left( \alpha \right) \left( t\right) \right) dt-\int _{0}^{T}e^{-\delta t}l_{\gamma }\left( y_{\gamma }\left( t;O,\alpha \right) ,\alpha \left( t\right) \right) dt\right| \\&\quad \le \int _{0}^{t_{y,O}}e^{-\delta t}\left| l_{\gamma }\left( y_{\gamma }\left( t;y,\mathcal {P}_{O,y}\left( \alpha \right) \right) ,\mathcal {P} _{O,y}\left( \alpha \right) \left( t\right) \right) \right| dt\\&\qquad +\int _{0}^{t_{y,O}}e^{-\delta t}\left| l_{\gamma }\left( y_{\gamma }\left( t;O,\alpha \right) ,\alpha \left( t\right) \right) \right| dt\\&\qquad +\mathbf {1}_{T>t_{y,O}}\left( 1-e^{-\delta t_{y,O}}\right) \int _{0}^{T-t_{y,O}}e^{-\delta t}\left| l_{\gamma }\left( y_{\gamma }\left( t;O,\alpha \right) ,\alpha \left( t\right) \right) \right| dt\\&\qquad +\mathbf {1}_{T>t_{y,O}}\int _{T-t_{y,O}}^{T}e^{-\delta t}\left| l_{\gamma }\left( y_{\gamma }\left( t;O,\alpha \right) ,\alpha \left( t\right) \right) \right| dt\\&\quad \le 2\left| l\right| _{0}\frac{\left| y\right| ^{1-\kappa } }{\left( 1-\kappa \right) \beta }+\frac{1}{\delta }\left| l\right| _{0}\left( 1-e^{-\delta \frac{\left| y\right| ^{1-\kappa }}{\left( 1-\kappa \right) \beta }}\right) +\left| l\right| _{0}\frac{\left| y\right| ^{1-\kappa }}{\left( 1-\kappa \right) \beta }\\&\quad \le 4\left| l\right| _{0}\frac{\left| y\right| ^{1-\kappa } }{\left( 1-\kappa \right) \beta }\le \frac{4\left| l\right| _{0} }{\left( 1-\kappa \right) \beta }\rho _{\varepsilon }^{2}. \end{aligned}$$

(ii) If $\alpha \in \mathcal {A}_{ad},$ then we set

$$\begin{aligned} \mathcal {P}_{\left( O,\gamma \right) }\left( \alpha \right) \left( t;y,\eta \right) =\left\{ \begin{array}{l} \mathcal {P}_{O,y}\left( \alpha \left( t;O,\gamma \right) \right) \text { if }\eta =\gamma ,\left| y\right| \le \rho _{\varepsilon }^{\frac{2}{1-\kappa }},\\ \alpha \left( t;y,\eta \right) ,\text { otherwise.} \end{array} \right. \end{aligned}$$

One only needs to notice that $y\mapsto t_{y,O}$ is Borel measurable to deduce that $\mathcal {P}_{O,\gamma }\left( \alpha \right) \in \mathcal {A}_{ad}.$ In the other cases, the construction is similar. We will just hint the measurability properties needed to insure that the constructed function $\mathcal {P}_{\left( x,\gamma \right) }\left( \alpha \right)$ is Borel measurable in $\left( t,y,\eta \right)$.

(b) If $y=O$, we distinguish two cases :

(b1) The road is “inactive”. Then, we introduce $t_{x,O}\left( \alpha \right) :=\inf \left\{ t>0:y_{\gamma }\left( t;x,\alpha \right) =O\right\}$ and define, if it is finite

$$\begin{aligned} \mathcal {P}_{x,y}\left( \alpha \right) \left( t\right) :=a_{\gamma ,1} ^{0}\mathbf {1}_{\left[ 0,t_{x,O}\left( \alpha \right) \right] }\left( t\right) +\alpha \left( t\right) \mathbf {1}_{(t_{x,O}\left( \alpha \right) ,\infty )}\left( t\right) , \end{aligned}$$

where $a_{\gamma ,1}^{0}$ is given by (Ab). Then, due to (Ab), it is clear that

$$\begin{aligned} \left| y_{\gamma }\left( t;y,\mathcal {P}_{x,y}\left( \alpha \right) \right) -y_{\gamma }\left( t;x,\alpha \right) \right| \le \left| x-y\right| \le \rho _{\varepsilon }^{2}, \end{aligned}$$

if $t\le t_{x,O}\left( \alpha \right)$ and

$$\begin{aligned} \left| y_{\gamma }\left( t;y,\mathcal {P}_{x,y}\left( \alpha \right) \right) -y_{\gamma }\left( t;x,\alpha \right) \right| =0, \end{aligned}$$

otherwise. We note that $y_{\gamma }\left( t;y,\mathcal {P}_{x,y}\left( \alpha \right) \right) =O$, for $t\le t_{x,O}\left( \alpha \right) .$ Thus, the assumption (Ac) yields

$$\begin{aligned}&\left| \int _{0}^{T}e^{-\delta t}l\left( y_{\gamma }\left( t;y,\mathcal {P}_{x,y}\left( \alpha \right) \right) ,\mathcal {P}_{x,y}\left( \alpha \right) \left( t\right) \right) dt-\int _{0}^{T}e^{-\delta t}l\left( y_{\gamma }\left( t;x,\alpha \right) ,\alpha \left( t\right) \right) dt\right| \\&\quad \le \int _{0}^{T}e^{-\delta t}Lip(l)\left| x-y\right| dt\le \frac{Lip(l)}{\delta }\left| x-y\right| \le \frac{Lip(l)}{\delta } \rho _{\varepsilon }^{2}. \end{aligned}$$

(b2) The road is “active”. Then, we introduce Similar to (a), one easily proves that $t_{y,x}\le \frac{\rho _{\varepsilon }^{2}}{\beta }.$ In this case, we define

$$\begin{aligned} \mathcal {P}_{x,y}\left( \alpha \right) \left( t\right) :=a_{\gamma ,1} ^{+}\mathbf {1}_{\left[ 0,t_{y,x}\right] }\left( t\right) +\alpha \left( t-t_{y,x}\right) \mathbf {1}_{(t_{y,x},\infty )}\left( t\right) , \end{aligned}$$

and get the same kind of estimates as in (a).

(c) We assume that $x\in J_{1}\cup \left\{ e_{1}\right\}$ and $y\in J_{1}.$ Then, $\alpha \in \mathcal {A}_{\gamma ,x}$ is admissible for y (at least for some small time). We define $t_{y}^{*}\left( \alpha \right) =\inf \left\{ t>0:y_{\gamma }\left( t;y,\alpha \right) \in \partial J_{1}\right\} \wedge \inf \left\{ t>0:y_{\gamma }\left( t;x,\alpha \right) =0\right\} \wedge t_{\varepsilon }.$ One notes, as before, that $y\mapsto t_{y}^{*}\left( \alpha \right)$ is Borel measurable.

(c1) If $t_{y}^{*}\left( \alpha \right) \ge t_{\varepsilon }$, then we let $\mathcal {P}_{x,y}\left( \alpha \right) (t):=\alpha (t)\mathbf {1}_{\left[ 0,t_{\varepsilon }\right) }\left( t\right) +\alpha _{0}\left( t;y_{\gamma }\left( t_{\varepsilon };y,\alpha \right) ,\gamma \right) \mathbf {1}_{\left[ t_{\varepsilon },\infty \right) }\left( t\right) ,$ where $\alpha _{0} \in \mathcal {A}_{ad}$ and have

$$\begin{aligned} \left| y_{\gamma }\left( t;y,\mathcal {P}_{x,y}\left( \alpha \right) \right) -y_{\gamma }\left( t;x,\alpha \right) \right| \le e^{Lip(f)t} \left| x-y\right| \le \sqrt{\left| x-y\right| }\le \rho _{\varepsilon }^{\frac{1}{1-\kappa }}, \end{aligned}$$

for all $t\le t_{\varepsilon }.$ Also, one easily gets, for every $T\le t_{\varepsilon },$

$$\begin{aligned}&\left| \int _{0}^{T}e^{-\delta t}l\left( y_{\gamma }\left( t;y,\mathcal {P}_{x,y}\left( \alpha \right) \right) ,\mathcal {P}_{x,y}\left( \alpha \right) \left( t\right) \right) dt-\int _{0}^{T}e^{-\delta t}l\left( y_{\gamma }\left( t;x,\alpha \right) ,\alpha \left( t\right) \right) dt\right| \\&\quad \le \frac{Lip\left( l\right) }{\delta }\sqrt{\left| x-y\right| }\le \frac{Lip\left( l\right) }{\delta }\rho _{\varepsilon }^{\frac{1}{1-\kappa }}. \end{aligned}$$

Since $\alpha _{0}\in \mathcal {A}_{ad},$ it follows that $\left( t,y\right) \mapsto \mathcal {P}_{x,y}\left( \alpha \right) (t)1_{t_{y}^{*}\left( \alpha \right) \ge t_{\varepsilon }}$ is Borel-measurable.

(c2) If $t_{y}^{*}\left( \alpha \right) <t_{\varepsilon }$ and $y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;y,\alpha \right) =e_{1}$, then, in particular, $\left| y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) -e_{1}\right| <\sqrt{\left| x-y\right| }\le \rho _{\varepsilon }^{\frac{1}{1-\kappa }}.$ Of course, this case is only interesting if $\alpha$ is no longer admissible. In particular, when $A_{\gamma ,e_{1}}\ne A^{\gamma ,1}.$ Then, we introduce $t_{e_{1} ,y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) }:=\inf \left\{ t\ge 0:y_{\gamma }\left( t;e_{1},a_{\gamma ,1}\right) =y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) \right\} .$ One has $t_{e_{1},y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) }\le \frac{\sqrt{\left| x-y\right| } }{\beta }.$ We define

$$\begin{aligned} \mathcal {P}_{x,y}\left( \alpha \right) \left( t\right)&:=\alpha \left( t\right) \mathbf {1}_{\left[ 0,t_{y}^{*}\left( \alpha \right) \right) }\left( t\right) +a_{\gamma ,1}\mathbf {1}_{\left[ t_{y}^{*}\left( \alpha \right) ,t_{y}^{*}\left( \alpha \right) +t_{e_{1},y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) }\right] }\left( t\right) \\&\quad +\alpha \left( t-t_{e_{1},y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) }\right) \mathbf {1}_{\left( t_{y}^{*}\left( \alpha \right) +t_{e_{1},y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) },\infty \right) }\left( t\right) . \end{aligned}$$

The functions $y\mapsto t_{y}^{*}\left( \alpha \right) ,$ $y\mapsto y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;y,\alpha \right)$ are Borel measurable. Hence, so is $y\mapsto t_{e_{1},y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) }$. It follows that

$$\begin{aligned} \left( t,y\right) \mapsto \mathcal {P}_{x,y}\left( \alpha \right) (t)\mathbf {1}_{t_{y}^{*}\left( \alpha \right) <t_{\varepsilon },\text { }y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;y,\alpha \right) =e_{1}} \end{aligned}$$

is also Borel-measurable. One has

$$\begin{aligned} \left| y_{\gamma }\left( t;y,\mathcal {P}_{x,y}\left( \alpha \right) \right) -y_{\gamma }\left( t;x,\alpha \right) \right| \le \sqrt{\left| x-y\right| }, \end{aligned}$$

if $t\le t_{y}^{*}\left( \alpha \right) ,$

$$\begin{aligned} \left| y_{\gamma }\left( t;y,\mathcal {P}_{x,y}\left( \alpha \right) \right) -y_{\gamma }\left( t;x,\alpha \right) \right|&\le \left| y_{\gamma }\left( t-t_{y}^{*}\left( \alpha \right) ;e_{1},a_{\gamma ,1}\right) -e_{1}\right| \\&\quad +\left| e_{1}-y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) \right| \\&\quad +\left| y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) -y_{\gamma }\left( t;x,\alpha \right) \right| \\&\le \left( \frac{2\left| f\right| _{0}}{\beta }+1\right) \sqrt{\left| x-y\right| }, \end{aligned}$$

if $t\in \left[ t_{y}^{*}\left( \alpha \right) ,t_{y}^{*}\left( \alpha \right) +t_{e_{1},y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) }\right] .$ Finally, if $t>t_{y}^{*}\left( \alpha \right) +t_{e_{1},y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) },$ then

$$\begin{aligned}&\left| y_{\gamma }\left( t;y,\mathcal {P}_{x,y}\left( \alpha \right) \right) -y_{\gamma }\left( t;x,\alpha \right) \right| \\&\quad =\left| \begin{array}{c} y_{\gamma }\left( t-t_{y}^{*}\left( \alpha \right) +t_{e_{1},y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) };y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) ,\mathcal {\alpha }\left( t_{y}^{*}\left( \alpha \right) +\cdot \right) \right) \\ -y_{\gamma }\left( t-t_{y}^{*}\left( \alpha \right) ;y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) ,\alpha \left( t_{y}^{*}\left( \alpha \right) +\cdot \right) \right) \end{array} \right| \\&\quad \le \left| f\right| _{0}\frac{\sqrt{\left| x-y\right| } }{\beta }. \end{aligned}$$

Moreover, if $T\le t_{\varepsilon },$ one gets (similar to (a)),

$$\begin{aligned}&\left| \int _{0}^{T}e^{-\delta t}l\left( y_{\gamma }\left( t;y,\mathcal {P}_{x,y}\left( \alpha \right) \right) ,\mathcal {P}_{x,y}\left( \alpha \right) \left( t\right) \right) dt-\int _{0}^{T}e^{-\delta t}l\left( y_{\gamma }\left( t;x,\alpha \right) ,\alpha \left( t\right) \right) dt\right| \\&\quad \le \int _{0}^{t_{y}^{*}\left( \alpha \right) }e^{-\delta t}Lip\left( l\right) \sqrt{\left| x-y\right| }dt+\frac{4\left| l\right| _{0}}{\beta }\sqrt{\left| x-y\right| }. \end{aligned}$$

(c3) The case $t_{y}^{*}\left( \alpha \right) <t_{\varepsilon }$ and $y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;y,\alpha \right) =O.$ In particular, one gets $\left| y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) \right| \le \sqrt{\left| x-y\right| }\le \rho _{\varepsilon }^{\frac{1}{1-\kappa }}.$

(c3.1) In the “active case”, we consider $t_{O,y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) }=\inf \left\{ t>0:y_{\gamma }\left( t;O,a_{\gamma ,1}^{+}\right) =y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) \right\}$ and define

$$\begin{aligned} \mathcal {P}_{x,y}\left( \alpha \right) \left( t\right)&:=\alpha \left( t\right) \mathbf {1}_{\left[ 0,t_{y}^{*}\left( \alpha \right) \right) }\left( t\right) +a_{\gamma ,1}^{+}\mathbf {1}_{\left[ t_{y}^{*}\left( \alpha \right) ,t_{y}^{*}\left( \alpha \right) +t_{O,y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) }\right] }\left( t\right) \\&\quad +\alpha \left( t-t_{O,y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) }\right) \mathbf {1}_{\left( t_{y}^{*}\left( \alpha \right) +t_{O,y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) },\infty \right) }\left( t\right) . \end{aligned}$$

One gets the same estimates (and measurability properties) as in (c2).

(c3.2) The “inactive case” is similar to (b1). We consider

$$\begin{aligned} \mathcal {P}_{x,y}\left( \alpha \right) \left( t\right)&:=\alpha \left( t\right) \mathbf {1}_{\left[ 0,t_{y}^{*}\left( \alpha \right) \right) }\left( t\right) +a_{\gamma ,1}^{0}\mathbf {1}_{\left[ t_{y}^{*}\left( \alpha \right) ,t_{y}^{*}\left( \alpha \right) +t_{y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) ,O}\right] }\left( t\right) \\&\quad +\alpha \left( t-t_{y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) ,O}\right) \mathbf {1}_{t_{y}^{*}\left( \alpha \right) +t_{y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) ,O},\infty }\left( t\right) , \end{aligned}$$

for all $t\ge 0.$ The functions $y\mapsto t_{y}^{*}\left( \alpha \right) ,$ $y\mapsto y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right)$ are Borel measurable. Hence, so is $y\mapsto t_{y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) ,O}\left( a_{\gamma ,1}^{0}\right)$. It follows that

$$\begin{aligned} \left( t,y\right) \mapsto \mathcal {P}_{x,y}\left( \alpha \right) (t)\mathbf {1}_{t_{y}^{*}\left( \alpha \right) <t_{\varepsilon },\text { }y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;y,\alpha \right) =O} \end{aligned}$$

is also Borel-measurable.

One easily notes that

$$\begin{aligned} \left| y_{\gamma }\left( t;y,\mathcal {P}_{x,y}\left( \alpha \right) \right) -y_{\gamma }\left( t;x,\alpha \right) \right| \le \sqrt{\left| x-y\right| }\le \rho _{\varepsilon },\text { if }0\le t\le t_{y}^{*}\left( \alpha \right) +t_{y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) ,O}, \end{aligned}$$

and $y_{\gamma }\left( t;y,\mathcal {P}_{x,y}\left( \alpha \right) \right) =y_{\gamma }\left( t;x,\alpha \right)$ if $t>t_{y}^{*}\left( \alpha \right) +t_{y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) ,O}.$ Using the assumption (Ac) on $\left[ t_{y}^{*}\left( \alpha \right) ,t_{y}^{*}\left( \alpha \right) +t_{y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) ,O}\right]$, one gets

$$\begin{aligned}&\left| \int _{0}^{T}e^{-\delta t}l\left( y_{\gamma }\left( t;y,\mathcal {P}_{x,y}\left( \alpha \right) \right) ,\mathcal {P}_{x,y}\left( \alpha \right) \left( t\right) \right) dt-\int _{0}^{T}e^{-\delta t}l\left( y_{\gamma }\left( t;x,\alpha \right) ,\alpha \left( t\right) \right) dt\right| \\&\quad \le \int _{0}^{t_{y}^{*}\left( \alpha \right) }\!e^{-\delta t}Lip\left( l\right) \sqrt{\left| x-y\right| }dt+\int _{t_{y}^{*}\left( \alpha \right) }^{\left( t_{y}^{*}\left( \alpha \right) +t_{y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) ,O}\right) \wedge T}e^{-\delta t}Lip(l)\sqrt{\left| x-y\right| }dt\\&\quad \le \frac{1}{\delta }Lip(l)\sqrt{\left| x-y\right| }. \end{aligned}$$

(c4) If $t_{y}^{*}\left( \alpha \right) <t_{\varepsilon }$ and $y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;x,\alpha \right) =O,$ then we proceed as in (a). We let

$$\begin{aligned} t_{y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;y,\alpha \right) ,O}:=\inf \left\{ t\ge 0:y_{\gamma }\left( t;y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;y,\alpha \right) ,a_{\gamma ,1}^{-}\right) =O\right\} . \end{aligned}$$

Obviously, $t_{y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;y,\alpha \right) ,O}\le \frac{\sqrt{\left| x-y\right| }^{1-\kappa } }{\left( 1-\kappa \right) \beta }.$ We set

$$\begin{aligned} \mathcal {P}_{x,y}\left( \alpha \right) \left( t\right)&:=\alpha \left( t\right) \mathbf {1}_{\left[ 0,t_{y}^{*}\left( \alpha \right) \right) }\left( t\right) +a_{\gamma ,1}^{-}\mathbf {1}_{\left[ t_{y}^{*}\left( \alpha \right) ,t_{y}^{*}\left( \alpha \right) +t_{y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;y,\alpha \right) ,O}\right] }\left( t\right) \\&\quad +\alpha \left( t-t_{y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;y,\alpha \right) ,O}\right) \mathbf {1}_{t_{y}^{*}\left( \alpha \right) +t_{y_{\gamma }\left( t_{y}^{*}\left( \alpha \right) ;y,\alpha \right) ,O},\infty }\left( t\right) , \end{aligned}$$

for all $t\ge 0$ and the estimates follow. The measurability properties hold as before.

(d) Finally, we assume that $y=e_{1}.$ Again, we only modify $\alpha$ if $A_{\gamma ,e_{1}}\ne A^{\gamma ,1}$. In this eventuality, we define $t_{e_{1},x}:=\inf \left\{ t\ge 0:y_{\gamma }\left( t;y,a_{\gamma ,1}\right) =x\right\} ,$ where $a_{\gamma ,1}$ appears in (Aa). Then $t_{e_{1},x}\le \frac{\left| x-y\right| }{\beta }.$ We let

$$\begin{aligned} \mathcal {P}_{x,e_{1}}\left( \alpha \right) \left( t\right) :=a_{\gamma ,1}\mathbf {1}_{\left[ 0,t_{e_{1},x}\right] }\left( t\right) +\alpha \left( t-t_{e_{1},x}\right) \mathbf {1}_{\left( t_{e_{1},x},\infty \right) }\left( t\right) . \end{aligned}$$

and get the conclusion.

The proof of our lemma is now complete. $\square$

1.2 Proof of Lemma 23

For any $y\in [O,(1+\varepsilon )e_{i}]$ (with $\gamma \in E_{i}^{active}$), we set

$$\begin{aligned} a_{\gamma ,i}^{\mathrm {opt},+}(y)=\underset{a\in A_{\gamma ,y}}{\mathrm {argmax} }\langle f_{\gamma }\left( y,a\right) ,e_{i}\rangle . \end{aligned}$$

It is clear that

$$\begin{aligned} \left\langle f_{\gamma }\left( y^{\prime },a\right) -f_{\gamma }\left( y,a_{\gamma ,i}^{\mathrm {opt},+}(y)\right) ,e_{i}\right\rangle\le & {} \underset{a^{\prime }\in A_{\gamma ,e_{i}}}{\sup }\left| f_{\gamma }\left( y^{\prime },a^{\prime }\right) -f_{\gamma }\left( y,a^{\prime }\right) \right| \nonumber \\\le & {} Lip\left( f\right) \left| y^{\prime }-y\right| ,\nonumber \\ \left\langle f_{\gamma }\left( y,a\right) -f_{\gamma }\left( y,a_{\gamma ,i}^{\mathrm {opt},+}(y)\right) ,e_{i}\right\rangle\le & {} 0, \end{aligned}$$

(20)

for all $y,y^{\prime }\in [O,(1+\varepsilon )e_{i}]$. We also let

$$\begin{aligned} d_{geo}\left( x,y\right) \!:=\!\left\{ \begin{array}{l} \left| x-y\right| ,\text { if }x,y\in \left[ -1-\varepsilon ,1+\varepsilon \right] e_{i},\\ \left| x\right| +\left| y\right| ,\text { if }x\in \left[ -1-\varepsilon ,1+\varepsilon \right] e_{i},y\in \left[ -1-\varepsilon ,1+\varepsilon \right] e_{j},\text { }i\ne j \end{array} \right. . \end{aligned}$$

Proof of Lemma 23

We will prove only the estimates on the trajectory. The estimates on the partial cost follow from the construction $\mathcal {P}_{x}\left( \alpha \right)$ which coincides with $\alpha$ except at the end points (where (C) applies; see also the similar condition (Ac) and the proof of Lemma 6). The assertion (ii) follows similar patterns to Lemma 6.

We aim at constructing $\tilde{\alpha }:=\mathcal {P}_{x}\left( \alpha \right) .$ We let $r_{0}\le \varepsilon$ (to be specified later on). We can assume, without loss of generality, that $x\ne O.$ (Should this not be the case, see Case 3). Then $\alpha$ is locally admissible. We set

$$\begin{aligned} \tau _{0}:=\inf \left\{ t\ge 0~:~d_{geo}\left( y_{\gamma }(t;x,\alpha ),{y_{\gamma }^{\rho _{\varepsilon }}\left( t;x,\overline{\alpha }\right) }\right) \ge r_{0}\right\} . \end{aligned}$$

If $\tau _{0}\ge t_{\varepsilon },$ the conclusion follows. Otherwise, the time where $y_{\gamma }$ meets again our target $y^{\rho _{\varepsilon }}$ will be referred to as “renewal time”. We give the construction of $\tilde{\alpha }$ on $[\tau _{0},t_{\varepsilon }]$ prior to renewal time. We let $\tau _{O}^{\varepsilon }$ be the exit time of the target from the branch,

$$\begin{aligned} \tau _{O}^{\varepsilon }=\inf \left\{ t\ge \tau _{0}~:~{y_{\gamma }^{\rho _{\varepsilon }}\left( t;x,\overline{\alpha }\right) }=O\right\} . \end{aligned}$$

(Hence, $\tau _{O}^{\varepsilon }>\tau _{0}$). Let us assume that $\tilde{\alpha }$ has been constructed up to some time $\tau _{0}\le t^{*}\le \tau _{O}^{\varepsilon }$ before the renewal time such that

$$\begin{aligned} d_{geo}\left( y_{\gamma }^{*},y_{\gamma }^{\rho _{\varepsilon },*}\right) \le \omega _{\varepsilon }\left( t^{*},r_{0}\right) , \end{aligned}$$

(R)

where we used the notation $y_{\gamma }^{*}=y_{\gamma }\left( t^{*};x,\widetilde{\alpha }\right)$ and $y_{\gamma }^{\rho _{\varepsilon },*}=y_{\gamma }^{\rho _{\varepsilon }}\left( t^{*};x,\overline{\alpha }\right)$. Even if this is not crucial for the rest of the proof, note that renewal cannot occur before $\tau _{0}+\frac{r_{0}}{2|f|_{0}}$, so that this iterative procedure will be applied only a finite number of times.

Case 1 $y_{\gamma }$ and $y_{\gamma }^{\rho _{\varepsilon }}$ are on the same branch (say $\left[ O,(1+\varepsilon )e_{1}\right] ;$ the case when $y_{\gamma }$ and $y^{\rho _{\varepsilon }}$ are on a “new” branch $\left[ O,-\varepsilon e_{1}\right]$ is similar), and $y_{\gamma }$ lies between the junction O and $y_{\gamma }^{\rho _{\varepsilon }}$ (i.e. $0\le \langle y_{\gamma }^{*},e_{1}\rangle <\langle y_{\gamma }^{\rho _{\varepsilon },*},e_{1}\rangle$). We let

$$\begin{aligned} t_{out}&=\inf \left\{ t\ge 0:y_{\gamma }\left( t;y_{\gamma }^{*} ,\alpha (t^{*}+\cdot )\right) =\left( 1+\varepsilon \right) e_{1}\right\} ,\;\;\\ t_{out}^{\rho _{\varepsilon }}&=\inf \left\{ t\ge 0:y_{\gamma } ^{\rho _{\varepsilon }}\left( t;y_{\gamma }^{{\rho _{\varepsilon }},*},\overline{\alpha }(t^{*}+\cdot )\right) =\left( 1+\varepsilon \right) e_{1}\right\} ,\\ t_{0}^{\rho _{\varepsilon }}&=\inf \left\{ t\ge 0:y_{\gamma }^{\rho _{\varepsilon }}\left( t;y_{\gamma }^{\rho _{\varepsilon ,*}},\overline{\alpha }(t^{*}+\cdot )\right) =O\right\} ,\;\;\\ t_{0}&=\inf \left\{ t\ge 0:y_{\gamma }\left( t;y_{\gamma }^{*},\alpha (t^{*}+\cdot )\right) =O\right\} . \end{aligned}$$

Let us introduce $t_{act}=\min \left( t_{out},t_{out}^{\rho _{\varepsilon } },t_{0},t_{0}^{\rho _{\varepsilon }}\right)$. Obviously, prior to the renewal time,  only $t_{0}$ is relevant (since $t_{out},t_{0}^{\rho _{\varepsilon }}$ cannot occur without renewal and if $t_{out}^{\rho _{\varepsilon }}<t_{0},$ then $\alpha$ is still locally admissible for the follower $y_{\gamma }$). We distinguish between the cases

(a1) If $t_{act}>0$, we extend $\tilde{\alpha }$ by setting $\tilde{\alpha }(t)=\alpha \left( t\right)$, if $t^{*}<t\le t^{*}+t_{act}.$ Gronwall’s inequality yields

$$\begin{aligned} \left| y_{\gamma }\left( t;x,\tilde{\alpha }\right) -y_{\gamma } ^{\rho _{\varepsilon }}\left( t;x,\overline{\alpha }\right) \right| \le \omega _{\varepsilon }\left( t-t^{*};|y_{\gamma }^{*}-y_{\gamma } ^{\rho _{\varepsilon },*}|\right) , \end{aligned}$$

for all $t^{*}<t\le t^{*}+t_{act}$.

(a2) If $t_{act}=t_{0}=0$, then we necessarily have that $t_{0}^{\rho _{\varepsilon }}>0$. In this case $y_{\gamma }^{*}=O$ and $\langle y_{\gamma }^{\rho _{\varepsilon }}\left( t^{*};x,\overline{\alpha }\right) ,e_{1}\rangle >0$.

(a2.1) The active case (by far the most complicated) $\gamma \in E_{1} ^{active}$. In order to simplify our notations, denote, in this case, $a_{\gamma ,O}^{+}=a_{\gamma ,1}^{\mathrm {opt},+}(O)$. We introduce

$$\begin{aligned} {t}_{control}&=\inf \left\{ t>0~:~y_{\gamma }\left( t;,y_{\gamma }^{*},a_{\gamma ,O}^{+}\right) =r_{\varepsilon }^{\prime }e_{1}\right\} \\ {t}_{collision}&=\inf \left\{ t>0~:~y_{\gamma }\left( t;,y_{\gamma }^{*},a_{\gamma ,O}^{+}\right) =y_{\gamma }^{\rho _{\varepsilon }}\left( t^{*}+t;,y_{\gamma }^{\rho _{\varepsilon },*},\overline{\alpha }(t^{*} +\cdot )\right) \right\} \end{aligned}$$

Note that because of the continuity of the trajectories and since $r_{\varepsilon }^{\prime }>0$, we have ${t}_{control}>0$ and ${t} _{collision}>0$. We extend naturally $\tilde{\alpha }$ by setting

$$\begin{aligned} \tilde{\alpha }\left( t+t^{*}\right) =a_{\gamma ,O}^{+}\text {, if } t\in \left( 0,{t}_{collision}\wedge {t}_{control}\right] . \end{aligned}$$

With this extension, our assumptions guarantee that $\langle y_{\gamma }\left( t+t^{*};x,\tilde{\alpha }\right) ,e_{1}\rangle \ge Lip(f)\beta >0$ and the junction O is now a reflecting barrier for $t\mapsto y_{\gamma }(t;y_{\gamma }^{*},a_{\gamma ,O}^{+}).$ Note also that for any $t\le {t}_{collision} \wedge {t}_{control}$, we have $\langle y_{\gamma }^{\rho _{\varepsilon }}\left( t+t^{*};x,\overline{\alpha }\right) ,e_{1}\rangle >0$. For every $0<t\le t_{collision}\wedge t_{control}$, one uses (20) to get

$$\begin{aligned}&\left| y_{\gamma }^{\rho _{\varepsilon }}\left( t+t^{*};x,\overline{\alpha }\right) -y_{\gamma }\left( t+t^{*};x,\tilde{\alpha }\right) \right| =\left\langle y_{\gamma }^{\rho _{\varepsilon }}\left( t;y_{\gamma }^{\rho _{\varepsilon },*},\overline{\alpha }\left( t^{*}+\cdot \right) \right) -y_{\gamma }\left( t;y_{\gamma }^{*},a_{\gamma ,O}^{+}\right) ,e_{1}\right\rangle \\&\quad =\langle (y_{\gamma }^{\rho _{\varepsilon },*}-y_{\gamma }^{*} ),e_{1}\rangle +\int _{0}^{t}\left\langle f_{\gamma }^{\rho _{\varepsilon }}\left( y_{\gamma }^{\rho _{\varepsilon }}\left( s;y_{\gamma }^{\rho _{\varepsilon },*},\overline{\alpha }\left( t^{*}+\cdot \right) \right) ,\overline{\alpha }\left( t^{*}+\cdot \right) \right) \right. \\&\qquad \left. -f_{\gamma }\left( y_{\gamma }\left( s;y_{\gamma }^{*},a_{\gamma ,O}^{+}\right) ,a_{\gamma ,O}^{+}\right) ,e_{1}\right\rangle ds\\&\quad \le \langle (y_{\gamma }^{\rho _{\varepsilon },*}-y_{\gamma }^{*} ),e_{1}\rangle +\int _{0}^{t}Lip\left( f\right) \left( \rho _{\varepsilon }+\left| y_{\gamma }^{\rho _{\varepsilon }}\left( s+t^{*};x,\overline{\alpha }\right) -y_{\gamma }\left( s+t^{*};x,\tilde{\alpha }\right) \right| \right) ds\\&\qquad +\int _{0}^{t}\left[ \left\langle \begin{array}{l} f_{\gamma }\left( y_{\gamma }\left( s;y_{\gamma }^{*},a_{\gamma ,O} ^{+}\right) ,\alpha \left( t^{*}+\cdot \right) \right) -f_{\gamma }\left( O,a_{\gamma ,O}^{+}\right) \\ +f_{\gamma }\left( O,a_{\gamma ,O}^{+}\right) -f_{\gamma }\left( y_{\gamma }\left( s;y_{\gamma }^{*},a_{\gamma ,O}^{+}\right) ,a_{\gamma ,O} ^{+}\right) \end{array} ,e_{1}\right\rangle \right] ds\\&\quad \le \left| y_{\gamma }^{\rho _{\varepsilon },*}-y_{\gamma }^{*}\right| +Lip\left( f\right) \left[ \left( \rho _{\varepsilon }+2r_{\varepsilon }^{\prime }\right) t+\int _{0}^{t}\left| y_{\gamma } ^{\rho _{\varepsilon }}\left( s+t^{*};x,\overline{\alpha }\right) -y_{\gamma }\left( s+t^{*};x,\tilde{\alpha }\right) \right| ds\right] . \end{aligned}$$

Using Gronwall’s inequality and our assumptions on $r_{\varepsilon }^{\prime }$, we deduce that for any $0<t\le t_{control}\wedge t_{collision}$,

$$\begin{aligned} \left| y_{\gamma }\left( t+t^{*};x,\tilde{\alpha }\right) -y_{\gamma }^{\rho _{\varepsilon }}\left( t+t^{*};x,\overline{\alpha }\right) \right| \le \omega _{\varepsilon }\left( t;\left| y_{\gamma } ^{\rho _{\varepsilon },*}-y_{\gamma }^{*}\right| \right) . \end{aligned}$$

Thus, we have constructed an extension of $t\mapsto \tilde{\alpha }(t)$ satisfying (R) during an increment of some strictly positive time $t_{control}\wedge t_{collision}$.

(a2.2) In the inactive case, it suffices to continue with the control $\alpha$ (since, in this case, $f_{\gamma }\left( O,a\right) =0,$ for all $a\in A^{\gamma ,1}$) up till $t_{collision}$ (or $t_{\varepsilon }$).

Case 2 We use the same notations as in the first case and aim at giving the control when $\tilde{\alpha }$ has been constructed up to some time $\tau _{0}\le t^{*}\le \tau _{O}^{\varepsilon }$ such that renewal does not occur at $t^{*}$ and both motions are at time $t^{*}$ on the same active branch (say $\left[ O,(1+\varepsilon )e_{1}\right]$). Contrary to Case 1, in this case we are assuming that $0<\langle y_{\gamma }^{\rho _{\varepsilon },*},e_{1}\rangle <\langle y_{\gamma }^{*},e_{1}\rangle$. We distinguish the following cases

(b1) If $t_{act}>0$. In this case we proceed exactly as in case (a1) and get the same conclusion.

(b2) If $t_{act}=t_{out}=0$ then $y_{\gamma }^{*}=(1+\varepsilon )e_{1}$ and we have $t_{out}^{\rho _{\varepsilon }}>0$. This case is completely symmetric to case (a2.1) but with motions starting at $t^{*}$ near $(1+\varepsilon )e_{1}$. The conclusion is similar.

(The case when $y_{\gamma }^{*}=-\varepsilon e_{1}$ is similar to (a2.1) if $\gamma \in E_{1}^{active}$ and to (a2.2) in the inactive case.)

Case 3 Control when $y_{\gamma }^{\rho _{\varepsilon }}\left( t^{*};x,\overline{\alpha }\right) \in \left[ O,(1+\varepsilon )e_{j}\right]$ and $y_{\gamma }\left( t^{*};x,\alpha ^{*}\right) \in \left[ O,(1+\varepsilon )e_{i}\right]$ with $i\ne j$. In particular, the two points may be at the intersection or the target is at the intersection and the follower is not. We can assume, without loss of generality, that $\gamma \in E_{j}^{active}$. (Otherwise, recalling that we start at the same initial point, this situation can only happen if $y_{\gamma }^{\rho _{\varepsilon },*}=O$ and no active branch exists. Then, whatever the control, $y_{\gamma }$ can only get closer to O.) In this case, we introduce

$$\begin{aligned} \hat{t}_{O}&=\inf \left\{ t>0~:~y_{\gamma }\left( t;y_{\gamma }^{*},a_{\gamma ,i}^{-}\right) =O\right\} \\ \hat{t}_{collision}&=\inf \left\{ t>0~:~y_{\gamma }\left( t;y_{\gamma }^{*},a_{\gamma ,i}^{-}\right) =y_{\gamma }^{\rho _{\varepsilon }}\left( t^{*}+t;x,\overline{\alpha }\right) \right\} \end{aligned}$$

and we extend $t\mapsto \tilde{\alpha }\left( t\right)$ up to time $t^{*}+\hat{t}_{O}\wedge \hat{t}_{collision}$ by setting

$$\begin{aligned} \tilde{\alpha }(t)=a_{\gamma ,i}^{-}\text {, for }t^{*}<t<t^{*}+\hat{t} _{O}\wedge \hat{t}_{collision}. \end{aligned}$$

Since, by assumption, $d_{geo}\left( y_{\gamma }^{*},y_{\gamma } ^{\rho _{\varepsilon },*}\right) \le \omega _{\varepsilon }(t^{*};r_{0})$, we have that

$$\begin{aligned} 0<\hat{t}_{O}\wedge \hat{t}_{collision}\le \frac{\left( \omega _{\varepsilon }(t^{*};r_{0})\right) ^{1-\kappa }}{\left( 1-\kappa \right) \beta }. \end{aligned}$$

Hence, with this construction, we get

$$\begin{aligned} d_{geo}\left( y_{\gamma }\left( t;y_{\gamma }^{*},\tilde{\alpha }\right) ,y_{\gamma }^{\rho _{\varepsilon }}\left( t;y_{\gamma }^{\rho _{\varepsilon },*},\overline{\alpha }\right) \right) |\le \left( \frac{|f|_{0}}{\left( 1-\kappa \right) \beta }+1\right) \left( \omega _{\varepsilon }(t^{*} ;r_{0})\right) ^{1-\kappa }, \end{aligned}$$

for all $t<\hat{t}_{O}\wedge \hat{t}_{collision}$. If $\hat{t}_{O}=\hat{t} _{O}\wedge \hat{t}_{collision}$, we arrive at $y_{\gamma }\left( \hat{t} _{O};y_{\gamma }^{*},\tilde{\alpha }\right) =O$. If every road is inactive, we continue to stay at O.

(c1) If $y_{\gamma }^{\rho _{\varepsilon }}\left( \hat{t}_{O};y_{\gamma } ^{\rho _{\varepsilon },*},\overline{\alpha }\right) \ne O$ we are back to case 1 but with $r_{0}$ now replaced by $r_{0}^{\prime }$ lower than $\left( \frac{|f|_{0}}{\left( 1-\kappa \right) \beta }+1\right) \left( \omega _{\varepsilon }(t^{*};r_{0})\right) ^{1-\kappa }$ : even if there has been a deterioration of the distance between $y_{\gamma }$ and $y^{\rho _{\varepsilon }}$ (not exceeding $\left( \frac{|f|_{0}}{\left( 1-\kappa \right) \beta }+1\right) \left( \omega _{\varepsilon }(t^{*};r_{0})\right) ^{1-\kappa }$ because we are back to case 1, the situation of case 3 (and also the situation of (b2)) will never happen before some renewal time occurs. Consequently, in the situation of case 3 we are always allowed to take in (R) the same value for $r_{0}$ (and we choose $r_{0}=r_{\varepsilon } ^{\prime }$).

(c2) Finally, we assume $y_{\gamma }^{\rho _{\varepsilon }}\left( \hat{t} _{O};y_{\gamma }^{\rho _{\varepsilon },*},\overline{\alpha }\right) =O$. If every road is inactive, then $y_{\gamma }$ stays at O and $y_{\gamma } ^{\rho _{\varepsilon }}$ cannot go further than $\rho _{\varepsilon }$. Otherwise, let us assume that some $j^{\prime }$ is active. Then, we take $\tilde{\alpha }\left( t\right) =a_{\gamma ,j^{\prime }}^{+}$ for some very small (yet strictly positive) time $t^{*}+\hat{t}_{O}<t\le t^{*}+\hat{t}_{O} +\frac{r_{\varepsilon }^{\prime }}{2\left| f\right| _{0}}$ and get

$$\begin{aligned} d_{geo}\left( y_{\gamma }^{\rho _{\varepsilon }}\left( t;x,\overline{\alpha }\right) ,y_{\gamma }\left( t;x,\widetilde{\alpha }\right) \right) \le r_{\varepsilon }^{\prime }, \end{aligned}$$

which allows one to iterate.

Conclusion Gathering all these results, the constructed strategy $\tilde{\alpha }$ is such that

$$\begin{aligned} \left| y_{\gamma }\left( t;x,\tilde{\alpha }\right) -y_{\gamma } ^{\rho _{\varepsilon }}\left( t;x,\overline{\alpha }\right) \right| \le \omega _{\varepsilon }(t_{\varepsilon };\Phi (\varepsilon )). \end{aligned}$$

for any $t\le t_{\varepsilon }$ and the lemma is proven. $\square$

1.3 Some Hints on the Proof of Lemma 24

The reader is invited to note that, if (C) holds true, then $l\left( y,a\right) =l\left( \Pi _{\overline{\mathcal {G}}}\left( y\right) ,a\right) ,$for all $y\in \overline{\mathcal {G}}^{+,\varepsilon }$. Hence, the same kind of cost can be reached by :

• hurrying to O when the target is at O,  then wait for collision by

• staying at O when the target enters a fictive road from the intersection if a control a such that $f\left( O,a\right) =0$ exists (for example, in the inactive case).

• or mimic staying at O by making very small trips (see case (c2) of the previous Lemma);

• at $e_{1}:$

• if $\left\langle f\left( e_{1},a\right) ,e_{1}\right\rangle \le 0,$ for all a,  we are done, since the target will never enter $\left( 1,1+\varepsilon \right] e_{1}$ (recall we start from $\overline{\mathcal {G} }).$

• otherwise, there exists $\left\langle f\left( e_{1},\widetilde{a} \right) ,e_{1}\right\rangle >\beta ^{\prime }>0$ and, by our assumption, we also have $\left\langle f\left( e_{1},a_{\gamma ,1}\right) ,e_{1} \right\rangle <-\beta .$ Then, again, we mimic staying at $e_{1}$ by making very small trips until collision.

The same kind of assertion are valid for $\lambda$ and Q (notice the definition of these terms on “fictive” roads). The trajectories around O are close due to the $\varepsilon$ distance from $\overline{\mathcal {G} }^{+,\varepsilon }$ to $\overline{\mathcal {G}}$ and as in the previous argument, coming around the intersection can only occur once before collision.