Abstract
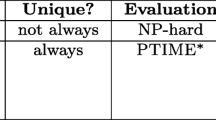
In this paper, we study the complexity of answering conjunctive queries (CQ) with inequalities (≠). In particular, we are interested in comparing the complexity of the query with and without inequalities. The main contribution of our work is a novel combinatorial technique that enables us to use any Select-Project-Join query plan for a given CQ without inequalities in answering the CQ with inequalities, with an additional factor in running time that only depends on the query. The key idea is to define a new projection operator, which keeps a small representation (independent of the size of the database) of the set of input tuples that map to each tuple in the output of the projection; this representation is used to evaluate all the inequalities in the query. Second, we generalize a result by Papadimitriou and Yannakakis (1997) and give an alternative algorithm based on the color-coding technique (2008) to evaluate a CQ with inequalities by using an algorithm for the CQ without inequalities. Third, we investigate the structure of the query graph, inequality graph, and the augmented query graph with inequalities, and show that even if the query and the inequality graphs have bounded treewidth, the augmented graph not only can have an unbounded treewidth but can also be NP-hard to evaluate. Further, we illustrate classes of queries and inequalities where the augmented graphs have unbounded treewidth, but the CQ with inequalities can be evaluated in poly-time. Finally, we give necessary properties and sufficient properties that allow a class of CQs to have poly-time combined complexity with respect to any inequality pattern. We also illustrate classes of queries where our query-plan-based technique outperforms the alternative approaches discussed in the paper.





Similar content being viewed by others
Notes
Some queries like q()=R(x)S(y) can be evaluated in constant time whereas to evaluate the inequality constraints we need to scan the relations in D.
Monien in [19] defines the notion of q-representatives for families of sets. Given a family of sets F, where each set has p elements, \(\hat F \subseteq F\) is a q-representative if for every set T of size q, there exists some set U∈F with \(U \cap T = \emptyset \) if and only if there exists a set \(\hat U \in \hat F\) such that \(\hat U \cap T = \emptyset \). Observe that a q-representative is a special case of an \(\mathcal {H}\)-equivalent relation: indeed, we can model the family F as a relation R F of arity p (where we do not care about the order of the attributes), and define \(\mathcal {H}\) as the full bipartite graph with edge set [p]×[q]. Then, if we write \(\mathcal {E}_{\mathcal {H}}(R^{F})\) back to a family of sets, it is a q-representative of F. Our techniques also generalize the notion of minimum samples presented in [8], which corresponds to \(\mathcal {H}\)-forbidden tuples of a relation in the case where \(\mathcal {H} = (X,Y,E)\) has |X|=|Y| and \(E(\mathcal {H})\) forms a perfect matching between X and Y. Several of the definitions and algorithmic ideas were inspired by both [8, 19].
From here on we let \(\mathcal {I}\) denote inequalities on attributes and not variables.
For the sake of simplicity, we do not write the bipartite graph as \(\mathcal {H} = (\bar {X}^{S}, \mathbf {A} \setminus \text {att}{S}, E)\). However, the transformation rules ensure that the edges E in the bipartite graph are always between \(\bar {X}^{S}\) and A∖attS.
s∘t denotes the concatenation of s,t.
The \(\log ^{2}(|D|)\) factor in Theorem 1 is reduced to \(\log (|D|)\) in Theorem 6, but this is because one \(\log \) factor was due to sorting the relations in the acyclic query, and now this hidden in the term T(|q|,|D|).
We use [p] to denote the set \(\{1, \dots ,p\}\).
Assuming includes only the attributes that appear as variables in the query q, ||≤|D||q|.
We can construct a bipartite graph where all vertices v appear on one side, the colors appear on the other side, and there is an edge (v,c) if c∈L(v). Then the list coloring problem on complete graph is solvable if and only if there is a perfect matching in the graph.
For example, for the complete graph on k vertices, the maximum integer vertex packing is of size 1 whereas the maximum fractional vertex packing is of size \(\frac {k}{2}\).
References
Abiteboul, S., Hull, R., Vianu, V.: Foundations of databases Addison-Wesley, 1995.
Afrati, F., Li, C., Mitra, P.: Answering Queries Using Views with Arithmetic Comparisons. PODS, 209–220 (2002).
Alon, N., Yuster, R., Zwick, U.: Finding and counting given length cycles. Algorithmica. 17 (3), 209–223 (1997).
Alon, N., Yuster, R., Zwick, U.: Color Coding. Encyclopedia of Algorithms. Edited by: Kao, M.Y. Springer (2008).
Atserias, A., Grohe, M., Marx, D.: Size bounds and query plans for relational joins. FOCS 739–748, 2008.
Chekuri, C., Rajaraman, A.: Conjunctive query containment revisited. Theor. Comput. Sci. 239 (2), 211–229 (2000).
Demange, M., De Werra, D.: On some coloring problems in grids. Theor. Comput. Sci. 472, 9–27 (2013).
Durand, A., Grandjean, E.: The complexity of acyclic conjunctive queries revisited coRR abs/cs/0605008, 2006.
Flum, J., Frick, M., Grohe, M.: Query evaluation via tree-decompositions. J. ACM. 49 (6), 716–752 (2002).
Gottlob, G., Leone, N., Scarcello, F.: Hypertree Decompositions and Tractable Queries. PODS, 21–32 (1999).
Graham, M.: On the Universal Relation. Technical Report. University of Toronto, Ontario (1979).
Grohe, M., Marx, D.: Constraint Solving via Fractional Edge Covers. SODA, 289–298 (2006).
Jansen, K., Scheffler, P.: Generalized coloring for tree-like graphs. Discret. Appl. Math. 75 (2), 135–155 (1997).
Khayyat, Z., Lucia, W., Singh, M., Ouzzani, M., Papotti, P., Quiané-Ruiz, J., Tang, N., Kalnis, P.: Lightning fast and space efficient inequality joins. PVLDB. 8 (13), 2074–2085 (2015). http://www.vldb.org/pvldb/vol8/p2074-khayyat.pdf.
Klug, A.: On conjunctive queries containing inequalities. J. ACM. 35 (1), 146–160 (1988).
Kolaitis, P.G., Martin, D.L., Thakur, M.N.: On the Complexity of the Containment Problem for Conjunctive Queries with Built-In Predicates. PODS, 197–204 (1998).
Koutris, P., Milo, T., Roy, S., Suciu, D.: Answering Conjunctive Queries with Inequalities. ICDT, 76–93 (2015).
van der Meyden, R.: The complexity of querying indefinite data about linearly ordered domains. J. Comput. Syst. Sci. 54 (1), 113–135 (1997). doi:http://dx.doi.org/10.1006/jcss.1997.1455.
Monien, B.: How to Find Long Paths Efficiently. Analysis and Design of Algorithms for Combinatorial Problems, North-Holland Mathematics Studies, vol. 109, pp. 239–254. North-Holland. Edited by: Ausiello, G., Lucertini, M. (1985).
Ngo, H.Q., Porat, E., Ré, C., Rudra, A.: Worst-Case Optimal Join Algorithms: [Extended Abstract]. PODS, 37–48 (2012).
Papadimitriou, C.H., Yannakakis, M.: On the Complexity of Database Queries. PODS, 12–19 (1997).
Robertson, N., Seymour, P.: Graph minors. iii. planar tree-width. J. Comb. Theory B. 36 (1), 49–64 (1984).
Veldhuizen, T.L.: Triejoin: a Simple, Worst-Case Optimal Join Algorithm. ICDT, 96–106 (2014).
Yannakakis, M.: Algorithms for Acyclic Database Schemes. VLDB, 82–94 (1981).
Yu, C., Ozsoyoglu, M.Z.: An Algorithm for Tree-Query Membership of a Distributed Query. COMPSAC, 306–312 (1979).
Yuster, R., Zwick, U.: Finding even cycles even faster. SIAM J. Discrete Math. 10 (2), 209–222 (1997).
Author information
Authors and Affiliations
Corresponding author
Additional information
This work has been partially funded by the NSF awards IIS-1247469 and IIS-0911036, European Research Council under the FP7, ERC grant MoDaS, agreement 291071 and by the Israel Ministry of Science.
Rights and permissions
About this article
Cite this article
Koutris, P., Milo, T., Roy, S. et al. Answering Conjunctive Queries with Inequalities. Theory Comput Syst 61, 2–30 (2017). https://doi.org/10.1007/s00224-016-9684-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00224-016-9684-2