A parallel-in-time approach for wave-type PDEs

Abstract

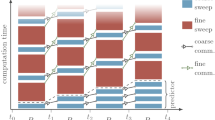
Numerical solutions to wave-type PDEs utilizing method-of-lines require the ODE solver’s stability domain to include a large stretch of the imaginary axis surrounding the origin. We show here that extrapolation based solvers of Gragg–Bulirsch–Stoer type can meet this requirement. Extrapolation methods utilize several independent time stepping sequences, making them highly suited for parallel execution. Traditional extrapolation schemes use all time stepping sequences to maximize the method’s order of accuracy. The present method instead maintains a desired order of accuracy while employing additional time stepping sequences to shape the resulting stability domain. We optimize the extrapolation coefficients to maximize the stability domain’s imaginary axis coverage. This yields a family of explicit schemes that approaches maximal time step size for wave propagation problems. On a computer with several cores we achieve both high order and fast time to solution compared with traditional ODE integrators.

Appendices

Appendix A Stability domains and imaginary axis coverage for some standard classes of ODE solvers

1.1 A.1 Stability domains and their significance for MOL time stepping

Fig. 10

Normalized stability domains for $\hbox {RK}_4$ (left) and $\hbox {RK}_8$ (right)

Each numerical ODE integration technique has an associated stability domain, defined as the region in a complex $\xi$-plane, with $\xi =h \lambda$, for which the ODE method does not have any growing solutions when it is applied to the constant coefficient ODE

$$\begin{aligned} y^{\prime }=\lambda y\,. \end{aligned}$$

(11)

For a one-step method the stability polynomial, here denoted $R(\xi )$, is the numerical solution after one step for Dahlquist’s test Eq. (11) [12]. The method’s stability domain is then

$$\begin{aligned} S=\{\xi \in {\mathbb {C}} : |R(\xi )| \le 1\}. \end{aligned}$$

(12)

When solving ODEs, the stability domain can provide a guide to the largest time step h that is possible without a decaying solution being misrepresented as a growing one. In the context of MOL-based approximations to a PDE of the form $\frac{\partial u}{\partial t}=L(x,t,u)$, the role of the stability domain becomes quite different, providing necessary and sufficient conditions for numerical stability under spatial and temporal refinement: all eigenvalues to the discretization of the PDE’s spatial operator L must fall within the solver’s stability domain. For wave-type PDEs, the eigenvalues of L will predominantly fall up and down the imaginary axis. As long as the time step h is small enough, this condition can be met for solvers that feature a positive ISB, but never for solvers with ISB = 0.

1.2 A.2 Runge–Kutta methods

All p-stage RK methods of order p feature the same stability domains when $p=1,2,3,4$—namely the first $p+1$ terms in the Taylor series for $e^\xi$. For higher orders of accuracy, more than p stages (function evaluations) are required to obtain order p. The $\text {R}\text {K}_{4}$ scheme used here is the classical one, and the $\text {R}\text {K}_{8}$ scheme is the one with 13 stages, introduced by Prince and Dormand [20], also given in [11] Table 6.4. Their normalized stability domains are shown in Fig. 10. Their ISBs are 2.8284 and 3.7023, respectively.

Appendix B ISB optimization algorithm

1.1 B.1 Optimization formulation

Let the extrapolated GBS stability polynomial be denoted $R(\xi )$, and the individual stability polynomials from each of m extrapolation components be denoted $P_i(\xi )$, which can be found in [6], Sect. 4.2. Then we have

$$\begin{aligned} R(\xi ) = \sum _{i=1}^m{c_iP_i(\xi )} \end{aligned}$$

(13)

for extrapolation weights $c_i$, $1 \le i \le m$. We collect the monomial coefficients of each $P_i(\xi )$ into the rows of a matrix, denoted $P(\xi )$. Then $R(\xi )$ can be more compactly expressed as $R(\xi )=c^TP(\xi )$. Now let the left-hand-side Vandermonde matrix from (3) be denoted V, and the right-hand-side constraint vector be denoted b. Then our order constraint Eq. (3) can be rewritten as $Vc=b$.

Denoting the time step size h, and given a curve $\varLambda \subset {\mathbb {C}}$, we specify the optimization problem as follows:

$$\begin{aligned} \begin{array}{lll} &{} \underset{c_1,c_2,\ldots ,c_m}{\text {maximize}} &{} h \\ &{} \text {subject to} &{} |R(h\lambda )|-1 \le 0, \; \forall \lambda \in \varLambda . \\ &{} &{} Vc = b \end{array} \end{aligned}$$

(14)

Following the work of Ketcheson and Ahmadia in [14], we reformulate the optimization problem in terms of an iteration over a convex subproblem. Minimizing the maximum value of $|R(h\lambda )|-1$ over the weights $c_i$ is a convex problem (see [14]). We therefore define the subproblem as follows:

$$\begin{aligned} \begin{array}{lll} &{} \underset{c_1,c_2,\ldots ,c_m}{\text {minimize}} &{} \mathop {\max }\limits _{\lambda \in \varLambda }{(|R(h\lambda )|-1)} \\ &{}\text {subject to} &{} Vc = b \end{array} \end{aligned}$$

(15)

Calling the minimax solution to (15) $r(h,\varLambda )$, we can now reformulate the optimization problem as:

$$\begin{aligned} \begin{array}{lll} &{} \underset{c_1,c_2,\ldots ,c_m}{\text {maximize}} &{} h \\ &{} \text {subject to} &{} r(h,\varLambda ) \le 0 \\ \end{array} \end{aligned}$$

(16)

The optimization routine was implemented with the CVX toolbox for MATLAB [10] using a bisection over time step h. Results presented in this paper use the software OPTISB [4] to optimize the stability domains.

1.2 B.2 Comparison to optimizing monomial coefficients

The main theoretical difference between our current algorithm and the algorithm presented in [14] is the basis over which coefficients are optimized. In [14] the authors optimize directly the coefficients to the stability polynomial in the monomial basis. This yields an optimal stability polynomial that must be approximated with a Runge–Kutta integrator. The polynomial is therefore fed into a second optimization routine to compute the Runge–Kutta coefficients.

In the extrapolation coefficient optimization we operate directly on linear combinations of the time stepper stability polynomials. The true optimal stability polynomial therefore may not be in the space of extrapolated GBS time stepper stability polynomials. However, the resulting stability polynomial is immediately realizable and we require no further optimization stage to generate our time stepping algorithm.

1.3 B.3 Implementing order constraints

To guarantee accuracy we require order constraints to be satisfied to machine precision. Most optimization routines accept equality constraints that will hold within a certain tolerance. Due to ill-conditioning of the Vandermonde systems we prefer to explicitly enforce the order constraints in the convex optimization. We split the stability polynomials into two groups which take on the “dep” and “free” subscripts, denoting dependent and optimized quantities, respectively. The dependent weights guarantee the extrapolation scheme achieves the specified order of accuracy. The remaining weights are our optimization variables. Thus the stability polynomial is computed as follows:

$$\begin{aligned} R(\xi ) = c_{\text {dep}}^TP_{\text {dep}}(\xi ) + c_{\text {free}}^TP_{\text {free}}(\xi ). \end{aligned}$$

(17)

Order constraints take the form (4) which yields the dependent weight computation (5). Splitting the weights apart reduces the number of design variables and, in practice, leads to better solutions than when utilizing equality constraints.