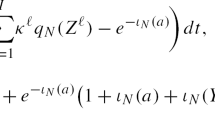Heterogeneity and learning with complete markets

Abstract

We study a complete markets endowment economy populated by two types of agents that have to learn equilibrium allocations. We show that market completeness allows agents to smooth consumption across states of nature, but not across time; as a result initial differences in beliefs induce persistent consumption imbalances that are not grounded in fundamentals. In some cases, these imbalances are not sustainable forever: the debt of one agent would grow unboundedly, and binding borrowing limits are necessary to prevent Ponzi schemes. Finally, we find that if a rational social planner attaches fixed Pareto weights to different individuals, financial autarky might be welfare superior to complete markets. The first best can be restored transferring consumption from the more optimistic agents to the others.

Appendix

Proof

(Proof of Proposition 1)

We start noting that rest points of Eq. (24) must satisfy the following condition:

$$\begin{aligned} \left( \begin{array}{c} \frac{\psi ^{1}}{\psi ^{1}+\psi ^{2}}-\psi ^{1} \\ \frac{\psi ^{2}}{\psi ^{1}+\psi ^{2}}-\psi ^{2} \end{array}\right) =0 \end{aligned}$$

(36)

Simple inspection confirms that, when $\psi ^{i}$s are between 0 and 1, the above equation is satisfied if and only if the $\psi ^{i}$s are in the set $\varPsi$ defined in the statement of the Proposition.

To check E-stability, we compute the Jacobian $DT-I$:

$$\begin{aligned} DT\left( \psi \right) -I =\left( \begin{array}{cc} \frac{\psi ^{2}}{\left( \psi ^{1}+\psi ^{2}\right) ^{2}}-1 &{} \frac{-\psi ^{1}}{\left( \psi ^{1}+\psi ^{2}\right) ^{2}} \\ \frac{-\psi ^{2}}{\left( \psi ^{1}+\psi ^{2}\right) ^{2}} &{} \frac{\psi ^{1}}{\left( \psi ^{1}+\psi ^{2}\right) ^{2}}-1 \end{array} \right) \end{aligned}$$

(37)

When evaluated at any of the points in $\varPsi$, it is easy to show that the eigenvalues of the above matrix are $-1$ and 0,¹⁹ hence completing the proof. $\square$

We now state and prove a short technical Lemma, which will be useful in the proof of Proposition 2

Lemma 2

Suppose that Assumption 2 holds, and let $\gamma ^{1}_{1}\left( R_{1}^{1}\right) ^{-1}\gtrless \gamma ^{2}_{1}\left( R_{1}^{2}\right) ^{-1}$. Then, $\gamma ^{1}_{t}\left( R_{t}^{1}\right) ^{-1}\gtrless \gamma ^{2}_{t}\left( R_{t}^{2}\right) ^{-1}$ for any $t>1$.

Proof

Let’s consider the random variable defined by:

$$\begin{aligned} G_{t}\equiv \gamma ^{1}_{t}\left( R_{t}^{1}\right) ^{-1}- \gamma ^{2}_{t}\left( R_{t}^{2}\right) ^{-1} \end{aligned}$$

Given the recursive law of motion of $R_{t}^{i}$ as described in Eq. (18), it can be rewritten as:

$$\begin{aligned} \frac{\gamma ^{1}_{t}R_{t-1}^{2}+\gamma ^{1}_{t}\gamma ^{2}_{t}\left( \left( \omega _{t-1}\right) ^{2}-R_{t-1}^{2} \right) - \gamma ^{2}_{t}R_{t-1}^{1} - \gamma ^{1}_{t}\gamma ^{2}_{t}\left( \left( \omega _{t-1}\right) ^{2}-R_{t-1}^{1} \right) }{R_{t}^{1} R_{t}^{2}} \end{aligned}$$

The above equation, together with some simple algebra, allows us to write:

$$\begin{aligned} G_{t}\gtrless 0 \; \Leftrightarrow \; \gamma ^{1}_{t}R_{t-1}^{2}\left( 1-\gamma ^{2}_{t}\right) - \gamma ^{2}_{t}R_{t-1}^{1}\left( 1-\gamma ^{1}_{t}\right) \gtrless 0 \end{aligned}$$

or, equivalently:

$$\begin{aligned} G_{t}\gtrless 0 \; \Leftrightarrow \; \frac{1-\gamma ^{2}_{t}}{1-\gamma ^{1}_{t}}\gtrless \frac{\gamma _{t}^{2}\left( R_{t-1}^{2}\right) ^{-1}}{\gamma _{t}^{1}\left( R_{t-1}^{1}\right) ^{-1}} \end{aligned}$$

(38)

Observe that the definition of the $\gamma ^{i}$’s, Eq. (19), implies that $1-\gamma ^{i}_{t}= \frac{\gamma ^{i}_{t}}{\gamma ^{i}_{t-1}}$, for $i=1,2$. Plugging this equivalent representation into Eq. (38), we get:

$$\begin{aligned} G_{t}\gtrless 0 \; \Leftrightarrow \; \frac{\frac{\gamma ^{2}_{t}}{\gamma ^{2}_{t-1}}}{\frac{\gamma ^{1}_{t}}{\gamma ^{1}_{t-1}}}\gtrless \frac{\gamma _{t}^{2}\left( R_{t-1}^{2}\right) ^{-1}}{\gamma _{t}^{1}\left( R_{t-1}^{1}\right) ^{-1}} \end{aligned}$$

which can be manipulated to conclude that:

$$\begin{aligned} G_{t}\gtrless 0 \; \Leftrightarrow \; G_{t-1}\gtrless 0 \end{aligned}$$

A trivial inductive argument completes the proof. $\square$

Proof

(Proof of Proposition 2)

First of all, note that $\frac{c_{t}^{1}}{c_{t}^{2}}=\frac{\psi _{t}^{1}}{\psi _{t}^{2}}$; moreover, using Eq. (17) the ratio $\frac{\psi _{t}^{1}}{\psi _{t}^{2}}$ can be written down recursively:

$$\begin{aligned} \frac{\psi _{t}^{1}}{\psi _{t}^{2}}= & {} \frac{\psi _{t-1}^{1} + \gamma _{t}^{1}\left( R_{t}^{1}\right) ^{-1}\omega _{t-1} \left( \frac{\psi _{t-1}^{1}}{\psi _{t-1}^{1}+\psi _{t-1}^{2}}\omega _{t-1} - \psi _{t-1}^{1}\omega _{t-1}\right) }{\psi _{t-1}^{2} + \gamma _{t}^{2}\left( R_{t}^{2}\right) ^{-1}\omega _{t-1} \left( \frac{\psi _{t-1}^{2}}{\psi _{t-1}^{1}+\psi _{t-1}^{2}}\omega _{t-1} - \psi _{t-1}^{2}\omega _{t-1}\right) } \\= & {} \frac{\psi _{t-1}^{1}}{\psi _{t-1}^{2}} \frac{\frac{\left( \psi _{t-1}^{1}+\psi _{t-1}^{2}\right) }{\left( \omega _{t-1}\right) ^{2}} +\gamma _{t}^{1}\left( R_{t}^{1}\right) ^{-1}\left( 1-\left( \psi _{t-1}^{1}+\psi _{t-1}^{2}\right) \right) }{\frac{ \left( \psi _{t-1}^{1}+\psi _{t-1}^{2}\right) }{\left( \omega _{t-1}\right) ^{2}} +\gamma _{t}^{2}\left( R_{t}^{2}\right) ^{-1}\left( 1-\left( \psi _{t-1}^{1}+\psi _{t-1}^{2}\right) \right) } \end{aligned}$$

which implies that, for any $t>0$:

$$\begin{aligned} \frac{\psi _{t}^{1}}{\psi _{t}^{2}}\gtrless \frac{\psi _{t-1}^{1}}{\psi _{t-1}^{2}} \; \Leftrightarrow \; \frac{\frac{\left( \psi _{t-1}^{1}+\psi _{t-1}^{2}\right) }{\left( \omega _{t-1}\right) ^{2}} +\gamma _{t}^{1}\left( R_{t}^{1}\right) ^{-1}\left( 1-\left( \psi _{t-1}^{1}+\psi _{t-1}^{2}\right) \right) }{\frac{ \left( \psi _{t-1}^{1}+\psi _{t-1}^{2}\right) }{\left( \omega _{t-1}\right) ^{2}} +\gamma _{t}^{2}\left( R_{t}^{2}\right) ^{-1}\left( 1-\left( \psi _{t-1}^{1}+\psi _{t-1}^{2}\right) \right) } \gtrless 1 \end{aligned}$$

Simple algebra shows that:

$$\begin{aligned} \frac{\frac{\left( \psi _{t-1}^{1}+\psi _{t-1}^{2}\right) }{\left( \omega _{t-1}\right) ^{2}} +\gamma _{t}^{1}\left( R_{t}^{1}\right) ^{-1}\left( 1-\left( \psi _{t-1}^{1}+\psi _{t-1}^{2}\right) \right) }{\frac{ \left( \psi _{t-1}^{1}+\psi _{t-1}^{2}\right) }{\left( \omega _{t-1}\right) ^{2}} +\gamma _{t}^{2}\left( R_{t}^{2}\right) ^{-1}\left( 1-\left( \psi _{t-1}^{1}+\psi _{t-1}^{2}\right) \right) } \gtrless 1 \end{aligned}$$

(39)

if and only if:

$$\begin{aligned} \left( \gamma _{t}^{1}\left( R_{t}^{1}\right) ^{-1}- \gamma _{t}^{2}\left( R_{t}^{2}\right) ^{-1}\right) \left[ 1- \left( \psi _{t-1}^{1}+\psi _{t-1}^{2}\right) \right] \gtrless 0 \end{aligned}$$

(40)

The condition (40) is written in terms of $\gamma ^{i}$’s, $R^{i}$’s and $\psi ^{i}$’s at time t, while the statement of the Proposition is in terms of initial confidence and beliefs. However, we know from Lemma 2 that if $\gamma _{1}^{1}\left( R_{1}^{1}\right) ^{-1} > (<)\gamma _{1}^{2}\left( R_{1}^{2}\right) ^{-1}$, then $\gamma _{t}^{1}\left( R_{t}^{1}\right) ^{-1} > (<)\gamma _{t}^{2}\left( R_{t}^{2}\right) ^{-1}$ for any $t<\infty$; hence, all remains to show is that, if $\psi _{0}^{1}+\psi _{0}^{2}> (<)1$, then $\psi _{t}^{1}+\psi _{t}^{2}\ge (\le )1$ for any $t<\infty$. To do this, we use equation (17) to obtain:

$$\begin{aligned} \psi _{t}^{1}+\psi _{t}^{2}= & {} \psi _{t-1}^{1} +\psi _{t-1}^{2} + \gamma _{t}^{1}\left( R_{t}^{1}\right) ^{-1} \left( \omega _{t-1}\right) ^{2}\left( \frac{\psi _{t-1}^{1}}{\psi _{t-1}^{1}+\psi _{t-1}^{2}} - \psi _{t-1}^{1} \right) \\&+\gamma _{t}^{2}\left( R_{t}^{2}\right) ^{-1} \left( \omega _{t-1}\right) ^{2}\left( \frac{\psi _{t-1}^{2}}{\psi _{t-1}^{1}+\psi _{t-1}^{2}} - \psi _{t-1}^{2} \right) \end{aligned}$$

Without loss of generality, let’s assume that $\gamma _{t}^{1}\left( R_{t}^{1}\right) ^{-1}> \gamma _{t}^{2}\left( R_{t}^{2}\right) ^{-1}$.²⁰ Starting from the above equation, simple algebra shows that:

$$\begin{aligned}&\psi _{t}^{1}+\psi _{t}^{2} \gtrless 1 \; \Leftrightarrow \; \psi _{t-1}^{1}+\psi _{t-1}^{2}-1\nonumber \\&\quad \gtrless \left( \psi _{t-1}^{2}-\frac{\psi _{t-1}^{2}}{\psi _{t-1}^{1}+\psi _{t-1}^{2}}\right) \left( \gamma _{t}^{2}\left( R_{t}^{2}\right) ^{-1}- \gamma _{t}^{1}\left( R_{t}^{1}\right) ^{-1}\right) \left( \omega _{t-1}\right) ^{2} \nonumber \\&\qquad +\left( \psi _{t-1}^{1}+\psi _{t-1}^{2}-1\right) \gamma _{t}^{1}\left( R_{t}^{1}\right) ^{-1} \left( \omega _{t-1}\right) ^{2} \end{aligned}$$

(41)

Since $\left( \gamma _{t}^{2}\left( R_{t}^{2}\right) ^{-1}-\gamma _{t}^{1}\left( R_{t}^{1}\right) ^{-1}\right) <0$ by Lemma 2, and $\gamma _{t}^{1}\left( R_{t}^{1}\right) ^{-1} \left( \omega _{t-1}\right) ^{2}<1$, equation (41) shows that $\psi _{t-1}^{1}+\psi _{t-1}^{2}>1$ implies that $\psi _{t}^{1}+\psi _{t}^{2}>1$. A trivial inductive argument completes the proof. $\square$

We now state and prove a Lemma which will be useful in the proof of Proposition 3.

Lemma 3

Suppose that Assumptions 1–2 hold, and let $A^{1}_{t}$ be defined as:

$$\begin{aligned} A_{t}^{1} = A_{t-1}^{1}\left( \frac{1}{\psi ^{1}_{t}+\psi ^{2}_{t}}\frac{\psi ^{1}_{t}}{\psi ^{1}_{t-1}}\right) ^{\sigma } \end{aligned}$$

(42)

with initial condition $A_{0}^{1}=1$, and with:

$$\begin{aligned} \psi _{t}^{i} = \psi _{t-1}^{i} + \gamma _{t}^{i}\left( c_{t-1}^{i} - \psi _{t-1}^{i} \right) \end{aligned}$$

Moreover, we assume that $\gamma ^{1}_{1}>\gamma ^{2}_{1}$. Then, the following holds:

$$\begin{aligned} \frac{\partial A^{1}_{t}}{\partial \psi ^{1}_{0}} \frac{1}{A_{t}^{1}}< \frac{\partial A^{1}_{t-1}}{\partial \psi ^{1}_{0}} \frac{1}{A_{t-1}^{1}} <0 \; \; \forall t>2 \end{aligned}$$

(43)

Proof

We proceed by induction. As a first step, we show that $\frac{\partial A^{1}_{1}}{\partial \psi ^{1}_{0}} \frac{1}{A_{1}^{1}}$ is negative ($\frac{\partial A^{1}_{0}}{\partial \psi ^{1}_{0}} \frac{1}{A_{0}^{1}}$ is trivially equal to zero). As a second step, we show that, if $\frac{\partial A^{1}_{t-1}}{\partial \psi ^{1}_{0}} \frac{1}{A_{t-1}^{1}} <0$, then $\frac{\partial A^{1}_{t}}{\partial \psi ^{1}_{0}} \frac{1}{A_{t}^{1}} < \frac{\partial A^{1}_{t-1}}{\partial \psi ^{1}_{0}} \frac{1}{A_{t-1}^{1}}$.

Step 1 We begin computing the following derivative:

$$\begin{aligned} \frac{\partial A^{1}_{1}}{\partial \psi ^{1}_{0}}= & {} \frac{\partial }{\partial \psi ^{1}_{0}}\left( \frac{1}{\psi ^{1}_{1}+\psi ^{2}_{1}}\frac{\psi ^{1}_{1}}{\psi ^{1}_{0}}\right) ^{\sigma } \nonumber \\= & {} \sigma \left( \frac{1}{\psi ^{1}_{1}+\psi ^{2}_{1}}\frac{\psi ^{1}_{1}}{\psi ^{1}_{0}}\right) ^{\sigma -1} \left\{ \frac{1}{\psi ^{1}_{1}+\psi ^{2}_{1}} \frac{\frac{\partial \psi ^{1}_{1}}{\partial \psi ^{1}_{0}} \psi ^{1}_{0}- \psi ^{1}_{1}}{\left( \psi ^{1}_{0}\right) ^2} \right. \nonumber \\&\left. - \frac{\psi ^{1}_{1}}{\psi ^{1}_{0}}\frac{1}{\left( \psi ^{1}_{1}+\psi ^{2}_{1}\right) ^2}\left( \frac{\partial \psi ^{1}_{1} }{\partial \psi ^{1}_{0}} + \frac{\partial \psi ^{2}_{1} }{\partial \psi ^{1}_{0}}\right) \right\} \end{aligned}$$

(44)

From the above equation, it is easy to see that a set of sufficient conditions for $\frac{\partial A^{1}_{1}}{\partial \psi ^{1}_{0}} \frac{1}{A_{1}^{1}}<0$ is:

• (i) $\frac{\partial \psi ^{1}_{1}}{\partial \psi ^{1}_{0}} \psi ^{1}_{0}- \psi ^{1}_{1} <0$;

• (ii) $\frac{\partial \psi ^{1}_{1} }{\partial \psi ^{1}_{0}} + \frac{\partial \psi ^{2}_{1} }{\partial \psi ^{1}_{0}} >0$.

In what follows, we show that such conditions are satisfied. To begin with, note that:

$$\begin{aligned} \frac{\partial \psi ^{1}_{1} }{\partial \psi ^{1}_{0}}= & {} 1+ \gamma ^{1}_{1}\left( \frac{\psi ^{1}_{0}+\psi ^{2}_{0}- \psi ^{1}_{0}}{\left( \psi ^{1}_{0}+\psi ^{2}_{0}\right) ^2}-1\right) \end{aligned}$$

(45)

$$\begin{aligned} \frac{\partial \psi ^{2}_{1} }{\partial \psi ^{1}_{0}}= & {} \gamma ^{2}_{1}\left( \frac{- \psi ^{2}_{0}}{\left( \psi ^{1}_{0}+\psi ^{2}_{0}\right) ^2}\right) \end{aligned}$$

(46)

From the above equations, we easily get that:

$$\begin{aligned} \frac{\partial \psi ^{1}_{1} }{\partial \psi ^{1}_{0}}=1- \gamma ^{1}_{1} +\gamma ^{1}_{1}\left( \frac{\psi ^{1}_{0}+\psi ^{2}_{0}- \psi ^{1}_{0}}{\left( \psi ^{1}_{0}+\psi ^{2}_{0}\right) ^2}\right) < 1- \gamma ^{1}_{1} +\gamma ^{1}_{1}\frac{1}{\psi ^{1}_{0}+\psi ^{2}_{0}} = \frac{\psi ^{1}_{1} }{\psi ^{1}_{0}} \end{aligned}$$

(47)

where the inequality is due to the fact that $\psi ^{1}_{0}>0$. Hence, the condition (i) is proved, since $\frac{\partial \psi ^{1}_{1} }{\partial \psi ^{1}_{0}} < \frac{\psi ^{1}_{1} }{\psi ^{1}_{0}}$ is equivalent to $\frac{\partial \psi ^{1}_{1}}{\partial \psi ^{1}_{0}} \psi ^{1}_{0}- \psi ^{1}_{1} <0$. Moreover, we have:

$$\begin{aligned} \frac{\partial \psi ^{1}_{1} }{\partial \psi ^{1}_{0}} + \frac{\partial \psi ^{2}_{1} }{\partial \psi ^{1}_{0}} = 1- \gamma ^{1}_{1} +\left( \gamma ^{1}_{1}- \gamma ^{2}_{1} \right) \frac{\psi ^{2}_{0}}{\left( \psi ^{1}_{0}+\psi ^{2}_{0}\right) ^2} >0 \end{aligned}$$

(48)

since $\gamma ^{1}_{1}> \gamma ^{2}_{1}$ by assumption. To sum up, we showed that (i) and (ii) hold, which implies that $\frac{\partial A^{1}_{1}}{\partial \psi ^{1}_{0}} \frac{1}{A_{1}^{1}}<0$.

Step 2 From the definition of $A^{1}_{t}$, it is easy to show that, when $t>0$:

$$\begin{aligned} \frac{\partial A^{1}_{t} }{\partial \psi ^{1}_{0}} \frac{1}{A^{1}_{t}} = \frac{\partial A^{1}_{t-1} }{\partial \psi ^{1}_{0}} \frac{1}{A^{1}_{t-1}} + \left[ \frac{\partial }{\partial \psi ^{1}_{0}}\left( \frac{1}{\psi ^{1}_{t}+\psi ^{2}_{t}}\frac{\psi ^{1}_{t}}{\psi ^{1}_{t-1}}\right) ^{\sigma } \right] \left( \frac{1}{\psi ^{1}_{t}+\psi ^{2}_{t}}\frac{\psi ^{1}_{t}}{\psi ^{1}_{t-1}}\right) ^{-\sigma } \end{aligned}$$

which implies that, if $\frac{\partial A^{1}_{t-1}}{\partial \psi ^{1}_{0}} \frac{1}{A_{t-1}^{1}} <0$, a sufficient condition for $\frac{\partial A^{1}_{t}}{\partial \psi ^{1}_{0}} \frac{1}{A_{t}^{1}} < \frac{\partial A^{1}_{t-1}}{\partial \psi ^{1}_{0}} \frac{1}{A_{t-1}^{1}}$ is the following:

$$\begin{aligned} \frac{\partial }{\partial \psi ^{1}_{0}}\left( \frac{1}{\psi ^{1}_{t}+\psi ^{2}_{t}}\frac{\psi ^{1}_{t}}{\psi ^{1}_{t-1}}\right) ^{\sigma } < 0 \end{aligned}$$

Let’s compute:

$$\begin{aligned} \frac{\partial }{\partial \psi ^{1}_{0}}\left( \frac{1}{\psi ^{1}_{t}+\psi ^{2}_{t}}\frac{\psi ^{1}_{t}}{\psi ^{1}_{t-1}}\right) ^{\sigma }= & {} \sigma \left( \frac{1}{\psi ^{1}_{t}+\psi ^{2}_{t}}\frac{\psi ^{1}_{t}}{\psi ^{1}_{t-1}}\right) ^{\sigma -1} \left[ \frac{1}{\psi ^{1}_{t}+\psi ^{2}_{t}} \frac{\frac{\partial \psi ^{1}_{t} }{\partial \psi ^{1}_{0}}\psi ^{1}_{t-1}-\frac{\partial \psi ^{1}_{t-1} }{\partial \psi ^{1}_{0}}\psi ^{1}_{t}}{\left( \psi ^{1}_{t-1}\right) ^2}\right. \nonumber \\&\left. - \frac{\psi ^{1}_{t}}{\psi ^{1}_{t-1}} \frac{1}{\left( \psi ^{1}_{t}+\psi ^{2}_{t}\right) ^2} \left( \frac{\partial \psi ^{1}_{t} }{\partial \psi ^{1}_{0}}+ \frac{\partial \psi ^{2}_{t} }{\partial \psi ^{1}_{0}}\right) \right] \end{aligned}$$

(49)

From the above equation, it is easy to see that a set of sufficient conditions for $\frac{\partial }{\partial \psi ^{1}_{0}}\left( \frac{1}{\psi ^{1}_{t}+\psi ^{2}_{t}}\frac{\psi ^{1}_{t}}{\psi ^{1}_{t-1}}\right) ^{\sigma } < 0$ is:

• (i) $\frac{\partial \psi ^{1}_{t} }{\partial \psi ^{1}_{0}}\psi ^{1}_{t-1}-\frac{\partial \psi ^{1}_{t-1} }{\partial \psi ^{1}_{0}}\psi ^{1}_{t} <0$;

• (ii) $\frac{\partial \psi ^{1}_{t} }{\partial \psi ^{1}_{0}}+ \frac{\partial \psi ^{2}_{t} }{\partial \psi ^{1}_{0}} >0$.

In what follows, we assume that these conditions hold at $t-1$, and show that this implies that they hold at t as well. To begin with, note that:

$$\begin{aligned} \frac{\partial \psi ^{1}_{t} }{\partial \psi ^{1}_{0}}= & {} \left( 1-\gamma ^{1}_{t}\right) \frac{\partial \psi ^{1}_{t-1} }{\partial \psi ^{1}_{0}} + \gamma ^{1}_{t}\left( \frac{\frac{\partial \psi ^{1}_{t-1} }{\partial \psi ^{1}_{0}}\left( \psi ^{1}_{t-1}+\psi ^{2}_{t-1}\right) - \psi ^{1}_{t-1}\left( \frac{\partial \psi ^{1}_{t-1} }{\partial \psi ^{1}_{0}}+ \frac{\partial \psi ^{2}_{t-1} }{\partial \psi ^{1}_{0}}\right) }{\left( \psi ^{1}_{t-1}+\psi ^{2}_{t-1}\right) ^2}\right) \\ \frac{\partial \psi ^{2}_{t} }{\partial \psi ^{1}_{0}}= & {} \left( 1-\gamma ^{2}_{t}\right) \frac{\partial \psi ^{2}_{t-1} }{\partial \psi ^{1}_{0}} + \gamma ^{2}_{t}\left( \frac{\frac{\partial \psi ^{2}_{t-1} }{\partial \psi ^{1}_{0}}\left( \psi ^{1}_{t-1}+\psi ^{2}_{t-1}\right) - \psi ^{2}_{t-1}\left( \frac{\partial \psi ^{1}_{t-1} }{\partial \psi ^{1}_{0}}+ \frac{\partial \psi ^{2}_{t-1} }{\partial \psi ^{1}_{0}}\right) }{\left( \psi ^{1}_{t-1}+\psi ^{2}_{t-1}\right) ^2}\right) \end{aligned}$$

From the expression for $\frac{\partial \psi ^{1}_{t} }{\partial \psi ^{1}_{0}}$ we obtain that:

$$\begin{aligned} \frac{\partial \psi ^{1}_{t}/\partial \psi ^{1}_{0}}{\partial \psi ^{1}_{t-1}/\partial \psi ^{1}_{0}}= & {} \left( 1-\gamma ^{1}_{t}\right) + \gamma ^{1}_{t}\left( \frac{\psi ^{2}_{t-1}- \psi ^{1}_{t-1}\frac{\partial \psi ^{2}_{t-1}/\partial \psi ^{1}_{t-1}}{\partial \psi ^{1}_{t-1}/\partial \psi ^{1}_{0}}}{\left( \psi ^{1}_{t-1}+\psi ^{2}_{t-1}\right) ^2}\right) \\< & {} \left( 1-\gamma ^{1}_{t}\right) + \gamma ^{1}_{t}\frac{1}{\psi ^{1}_{t-1}+\psi ^{2}_{t-1}} = \frac{\psi ^{1}_{t} }{\psi ^{1}_{t-1}} \end{aligned}$$

where the inequality is due to the fact that $\frac{\partial \psi ^{1}_{t-1} }{\partial \psi ^{1}_{0}}> - \frac{\partial \psi ^{2}_{t-1} }{\partial \psi ^{1}_{0}}$ by the induction hypothesis that $\frac{\partial \psi ^{1}_{t-1} }{\partial \psi ^{1}_{0}}+ \frac{\partial \psi ^{2}_{t-1} }{\partial \psi ^{1}_{0}} >0$. Hence, the condition (i) is proved, since $\frac{\partial \psi ^{1}_{t}/\partial \psi ^{1}_{0}}{\partial \psi ^{1}_{t-1}/\partial \psi ^{1}_{0}} < \frac{\psi ^{1}_{t} }{\psi ^{1}_{t-1}}$ is equivalent to $\frac{\partial \psi ^{1}_{t} }{\partial \psi ^{1}_{0}}\psi ^{1}_{t-1}-\frac{\partial \psi ^{1}_{t-1} }{\partial \psi ^{1}_{0}}\psi ^{1}_{t} <0$.

To show that condition (ii) is satisfied, we begin noting that, since $\gamma ^{1}_{t}>\gamma ^{2}_{t}$ ²¹ and $\frac{\partial \psi ^{2}_{t} }{\partial \psi ^{1}_{0}}$ is negative, we can bound the expression $\frac{\partial \psi ^{1}_{t} }{\partial \psi ^{1}_{0}}+ \frac{\partial \psi ^{2}_{t} }{\partial \psi ^{1}_{0}}$ as follows:

$$\begin{aligned} \frac{\partial \psi ^{1}_{t} }{\partial \psi ^{1}_{0}}+ \frac{\partial \psi ^{2}_{t} }{\partial \psi ^{1}_{0}}>\frac{\partial \psi ^{1}_{t} }{\partial \psi ^{1}_{0}}+ \frac{\gamma ^{1}_{t}}{\gamma ^{2}_{t}}\frac{\partial \psi ^{2}_{t} }{\partial \psi ^{1}_{0}} \end{aligned}$$

(50)

The variable in the RHS of the above inequality is positive for any t; in fact, using Eqs. (45) and (46) we get:

$$\begin{aligned} \frac{\partial \psi ^{1}_{1} }{\partial \psi ^{1}_{0}}+ \frac{\gamma ^{1}_{1}}{\gamma ^{2}_{1}}\frac{\partial \psi ^{2}_{1} }{\partial \psi ^{1}_{0}} = 1-\gamma ^{1}_{1}>0 \end{aligned}$$

(51)

Instead, for $t>1$, we can combine the expressions for $\frac{\partial \psi ^{1}_{t} }{\partial \psi ^{1}_{0}}$ and $\frac{\partial \psi ^{2}_{t} }{\partial \psi ^{1}_{0}}$ to derive:

$$\begin{aligned} \frac{\partial \psi ^{1}_{t} }{\partial \psi ^{1}_{0}}+ \frac{\gamma ^{1}_{t}}{\gamma ^{2}_{t}}\frac{\partial \psi ^{2}_{t} }{\partial \psi ^{1}_{0}}= & {} \left( 1-\gamma ^{1}_{t}\right) \frac{\partial \psi ^{1}_{t-1} }{\partial \psi ^{1}_{0}} + \left( 1-\gamma ^{2}_{t}\right) \frac{\gamma ^{1}_{t}}{\gamma ^{2}_{t}}\frac{\partial \psi ^{2}_{t-1} }{\partial \psi ^{1}_{0}} \nonumber \\= & {} \left( 1-\gamma ^{1}_{t}\right) \left( \frac{\partial \psi ^{1}_{t-1} }{\partial \psi ^{1}_{0}}+ \frac{\gamma ^{1}_{t-1}}{\gamma ^{2}_{t-1}}\frac{\partial \psi ^{2}_{t-1} }{\partial \psi ^{1}_{0}}\right) \end{aligned}$$

(52)

where we used the equality $1-\gamma ^{i}_{t}=\frac{\gamma ^{i}_{t}}{\gamma ^{i}_{t-1}}$, for $i=1,2$. Combining (51) and (52), a trivial inductive argument leads us to the conclusion that $\frac{\partial \psi ^{1}_{t} }{\partial \psi ^{1}_{0}}+ \frac{\gamma ^{1}_{t}}{\gamma ^{2}_{t}}\frac{\partial \psi ^{2}_{t} }{\partial \psi ^{1}_{0}} >0$; because of the bound (50), this implies that $\frac{\partial \psi ^{1}_{t} }{\partial \psi ^{1}_{0}}+ \frac{\partial \psi ^{2}_{t} }{\partial \psi ^{1}_{0}} >0$. To sum up, we showed that (i) and (ii) holds, which implies that $\frac{\partial A^{1}_{t}}{\partial \psi ^{1}_{0}}\frac{1}{A_{t}^{1}}< \frac{\partial A^{1}_{t-1}}{\partial \psi ^{1}_{0}}\frac{1}{A_{t-1}^{1}}<0$.

Combining Step 1 and Step 2, a trivial inductive argument completes the proof. $\square$

Proof

(Proof of Proposition 3)

We start by computing the derivative of $F^{1}\left( \cdot ; \psi _{0}^{2},\gamma _{1}^{2}, \gamma _{1}^{2}\right)$:

$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d}\psi _{0}^{1}}F^{1}\left( \psi _{0}^{1}; \psi _{0}^{2},\gamma _{1}^{2},\gamma _{1}^{2}\right) = \sum _{t=0}^{\infty } \beta ^{t} A_{t}^{1} \left[ \left( \frac{\psi _{t}^{1}}{\psi _{t}^{1}+ \psi _{t}^{2}}\right) ^{- \sigma } \frac{d}{d \psi _{0}^{1}}\left( \frac{\psi _{t}^{1}}{\psi _{t}^{1}+ \psi _{t}^{2}}\right) \right. \\&\quad +\left. \left( \frac{\psi _{t}^{1}}{\psi _{t}^{1}+ \psi _{t}^{2}} - \frac{1}{2} \right) \left( -\sigma \right) \left( \frac{\psi _{t}^{1}}{\psi _{t}^{1}+\psi _{t}^{2}}\right) ^{- \sigma -1}\frac{\hbox {d}}{\hbox {d}\psi _{0}^{1}}\left( \frac{\psi _{t}^{1}}{\psi _{t}^{1}+ \psi _{t}^{2}}\right) \right] \\&\quad +\sum _{t=0}^{\infty } \beta ^{t} \frac{\hbox {d}A_{t}^{1}}{\hbox {d} \psi _{0}^{1}}\left( \frac{\psi _{t}^{1}}{\psi _{t}^{1}+ \psi _{t}^{2}}\right) ^{- \sigma }\left( \frac{\psi _{t}^{1}}{\psi _{t}^{1}+ \psi _{t}^{2}} - \frac{1}{2} \right) \end{aligned}$$

which can be rewritten as the sum of three series:

$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d}\psi _{0}^{1}}F^{1}\left( \psi _{0}^{1}; \psi _{0}^{2},\gamma _{1}^{2}, \gamma _{1}^{2}\right) = \left\{ \frac{\sigma }{2}\sum _{t=0}^{\infty } \beta ^{t} A_{t}^{1} \left( \frac{\psi _{t}^{1}}{\psi _{t}^{1}+ \psi _{t}^{2}}\right) ^{- \sigma -1}\frac{\hbox {d}}{\hbox {d} \psi _{0}^{1}}\left( \frac{\psi _{t}^{1}}{\psi _{t}^{1}+ \psi _{t}^{2}}\right) \right\} \nonumber \\&\quad + \left\{ \left( 1- \sigma \right) \sum _{t=0}^{\infty } \beta ^{t} A_{t}^{1} \left( \frac{\psi _{t}^{1}}{\psi _{t}^{1}+ \psi _{t}^{2}}\right) ^{- \sigma }\frac{\hbox {d}}{\hbox {d} \psi _{0}^{1}}\left( \frac{\psi _{t}^{1}}{\psi _{t}^{1}+ \psi _{t}^{2}}\right) \right\} \nonumber \\&\quad +\left\{ \sum _{t=0}^{\infty } \beta ^{t} A_{t}^{1} \left( \frac{\psi _{t}^{1}}{\psi _{t}^{1}+ \psi _{t}^{2}}\right) ^{- \sigma }\left( \frac{\psi _{t}^{1}}{\psi _{t}^{1}+ \psi _{t}^{2}} - \frac{1}{2} \right) \left( \frac{\hbox {d} A_{t}^{1}}{\hbox {d}\psi _{0}^{1}} \frac{1}{A_{t}^{1}}\right) \right\} \end{aligned}$$

(53)

We implicitly assume that all the three series are convergent; this is done without loss of generality, since none of them can diverge to $-\infty$, and if any of them diverge to $+\infty$ the statement of the Proposition is trivially true.

Note that, since the derivative of agent 1 consumption with respect to her initial beliefs is positive, the first series is positive, and also the second one is (weakly) positive if $\sigma \in [0,1]$. To determine the sign of the third series, we start by observing that, since $\psi _{0}^{1}+ \psi _{0}^{2}>1$ and $\gamma _{1}^{1}> \gamma _{1}^{2}$, we know from Proposition 2 that the sequence $\left\{ \beta ^{t} A_{t}^{1} \left( \frac{\psi _{t}^{1}}{\psi _{t}^{1}+ \psi _{t}^{2}} - \frac{1}{2}\right) \right\}$ is such that its terms are positive for t smaller than some $\overline{T}<\infty$, and negative for $t> \overline{T}$. Moreover, by Lemma 3 we know that the terms of the sequence $\left\{ \frac{\mathrm{d}A_{t}^{1}}{\mathrm{d}\psi _{0}^{1}} \frac{1}{A_{t}^{1}}\right\}$ are negative and of increasing absolute value. Combining this two facts with the assumption that:

$$\begin{aligned} F^{1}\left( \psi _{0}^{1}; \psi _{0}^{2},\gamma _{1}^{2}, \gamma _{1}^{2}\right) = \sum _{t=0}^{\infty } \beta ^{t} A_{t}^{1} \left( \frac{\psi _{t}^{1}}{\psi _{t}^{1}+ \psi _{t}^{2}}\right) ^{- \sigma }\left( \frac{\psi _{t}^{1}}{\psi _{t}^{1}+ \psi _{t}^{2}} - \frac{1}{2} \right) =0 \end{aligned}$$

we conclude that the third series in (53) is positive, and hence also the sum of the three series is strictly positive if $\sigma \in [0,1]$; by continuity, there must exist a $\overline{\sigma }>1$ such that, if $\sigma \in [0, \overline{\sigma }]$ (and, consequently, the second series becomes negative) the sum of the three series remains strictly positive. This completes the proof of the Proposition. $\square$

Proof

(Proof of Proposition 5)

Here we sketch the proof, which is based on the fact that $u\left( 0\right) =-\infty$ when $\sigma \ge 1$, while $u\left( 1\right)$ is always finite. Hence, the term:

$$\begin{aligned} \alpha ^{1} \frac{\left( c_{t}^{1}\right) ^{1-\sigma }-1}{1-\sigma } + \alpha ^{2} \frac{\left( c_{t}^{2}\right) ^{1-\sigma }-1}{1-\sigma } \end{aligned}$$

(54)

in the social welfare function gets arbitrarily close to $-\infty$ when consumption of one of the two agents approaches zero. Given Proposition 2, if $\gamma _{1}^{1}= \gamma _{1}^{2}$ the consumption allocations remain at their initial level, as long as debt limits do not bind. Therefore, we can pick an initial distribution of beliefs $\psi _{0}$ such that $c^{1}$ is arbitrarily close to 0 as long as debt limits do not bind. By Lemma 1, the debt limit for agent 2 starts binding from some $T<\infty$, and we can set $\varepsilon$ so that $c^{2}$ is arbitrarily close to 0 from T on. This equilibrium is such that the term (54) is arbitrarily close to $-\infty$ for any t, which completes the proof. $\square$