Comparable characterizations of four solutions for permission tree games

Abstract

In the field of cooperative games, there is an extensive literature that studies situations of restricted cooperation. In a communication graph game, players can only cooperate if they are connected in an undirected graph representing the communication possibilities. The Myerson value of such a game is obtained by taking the Shapley value of the corresponding restricted game. For the special case that the graph is cycle-free and connected, for each player the corresponding hierarchical outcome yields an alternative solution. In a permission tree game, the player set is enriched with a rooted directed graph (or tree) on the set of players. A coalition is said to be feasible, if for every player in the coalition, except the top (root) player, also its predecessor belong(s) to the coalition. The permission value is obtained by taking the Shapley value of the associated restricted game. In this paper, we modify the Myerson value and hierarchical outcome that are defined for (undirected) communication graph games to a value for permission tree games. We also define a new solution that assigns all payoff to the unique top player in the hierarchy. Then comparable characterizations are given of these three solutions and the known permission value.

1 Introduction

A cooperative game with transferable utility, or simply a TU-game, consists of a finite set of players and a characteristic function that assigns a worth to any subset (coalition) of players. A (single-valued) solution is a function that assigns to every game a vector of individual payoffs to the players. One of the most applied efficient solutions for cooperative TU-games is the Shapley value (Shapley 1953).¹

A classical TU-game describes a situation in which any coalition of players can cooperate and earn its worth. However, in most economic and political organizations not every coalition is feasible. Therefore, in the literature various models involving restrictions on coalition formation have been developed. The well-known model of communication graph games, introduced by Myerson (1977), studies situations where it is no longer assumed that any coalition of players can cooperate because they are unable to communicate. Myerson models this by an undirected graph in which the links represent the communication relations between the players. A coalition is unrestricted with respect to cooperation, or feasible, if it is connected in the graph. The Myerson value for communication graph games is the solution that assigns to every communication graph game the Shapley value of its corresponding restricted game, being the game in which the worth of any coalition is given by the sum of the worths of its components within the graph. For cycle-free and connected communication graphs, Demange (2004) introduced the notion of hierarchical outcome. Given a player i, Demange considered the graph as a rooted tree with player i as the unique top player. Then the hierarchical outcome with respect to i is the payoff vector that assigns to any player its marginal contribution in the Myerson restricted game to the coalition of all its subordinates in the rooted tree. So, for any i there is a corresponding hierarchical outcome vector. Since for superadditive games each vector is in the core of the restricted game, Demange argued that ‘hierarchy yields stability.’

Restrictions on cooperation might also appear because players are part of a hierarchical organization. In games with a permission structure, the hierarchical organization is modeled by a directed graph. Cooperation is restricted in the sense that a player needs permission to cooperate from players that are higher in the hierarchy. In the conjunctive approach, introduced in Gilles et al. (1992), a coalition is feasible, if and only if for every player in the coalition also all its predecessors (in the directed graph) belong to the coalition. In the disjunctive approach, developed in Gilles and Owen (1994), a coalition is feasible if and only if for every player in the coalition at least one of his predecessors (if any) also belongs to the coalition. The conjunctively (disjunctively) restricted game is the TU-game in which the worth of a coalition is given by the worth of its maximal feasible subcoalition.²

We consider games with a permission structure that is given by a rooted tree, to be called permission tree games. In a rooted tree, each player has at most one predecessor, so the conjunctively and disjunctively restricted games coincide. We call this the permission restricted game. The permission value is the solution that assigns to any permission tree game the Shapley value of its corresponding permission restricted game. For permission tree games, van den Brink et al. (2015) introduced the Average Tree permission value and gave comparable axiomatizations of this value and the permission value.

In this paper we introduce three new solutions for permission tree games. First, we apply the Myerson value by assigning to every permission tree game the Myerson value of the underlying undirected communication graph game. Second, we define the hierarchical outcome of a permission tree game as the hierarchical outcome corresponding to the root (i.e., top player) of the permission tree. The third new solution assigns to every permission tree game the hierarchical outcome corresponding to the root of the permission restricted game. We provide a set of nine axioms to compare three new solutions with each other and with the permission value. It appears that all four solutions satisfy five of the nine axioms and that each solution is characterized by these five axioms and precisely two of the remaining four axioms. Moreover, five axioms are incompatible with two remaining combinations of two of the four other axioms.

A typology of four solutions is made, based on a number of criteria. The cooperation restrictions underlying the Myerson value and the hierarchical outcome give the hierarchy some flavor of communication according to these solutions. Players located at upper levels of the hierarchy serve to connect players at lower levels, but players who are not connecting lower level players do not need to give permission to these players. Coalitions can be feasible even if not all predecessors are present. On the other hand, according to the permission value and the top value the hierarchy has the flavor of a permission structure. Coalitions are only feasible if for all players their predecessors are also present. Considering the distribution of payoff, the Myerson value and the permission value have in common that they treat players, that are in some sense equally important in generating worth under their respective cooperation restrictions, equally. The hierarchical outcome and top value have in common that they assign payoffs fully to their respective top players (being the root player as global top for the top value, and the local top player who is the highest in connecting a coalition for the hierarchical outcome).

The paper is organized as follows. Section 2 consists of preliminaries on cooperative TU-games, digraphs and permission tree games. Section 3 gives four solutions for permission tree games, and Sect. 4 gives the axioms and the characterization results. In Sect. 5, the typology of the four solutions is discussed.

2 Preliminaries

2.1 Cooperative TU-games

A cooperative game with transferable utility, or simply a TU-game, is a pair (N, v), where is a finite set of players and is a characteristic function on N satisfying $v(\emptyset ) = 0$. For any coalition $S \subseteq N$, v(S) is the worth that coalition S can obtain from cooperation. For game (N, v) and $S \subseteq N$, $(S,v_S)$ denotes the subgame of (N, v) on S, given by $v_S(T) = v(T)$, $T \subseteq S$. For $i \in N$, we denote $N \setminus \{i\}$ by $N_{-i}$ and the subgame $(N_{-i},v_{N_{-i}})$ by $(N_{-i},v_{-i})$. Game (N, v) is monotone if $v(S) \le v(T)$ when $S \subseteq T \subseteq N$. We denote by ${\mathcal {G}}$ and ${\mathcal {G}}_M$, respectively, the class of all TU-games and all monotone TU-games.

For two games $(N,v), (N,w) \in {\mathcal {G}}$, the game $(N,v+w)$ is given by $(v+w)(S)=v(S)+w(S)$ for all $S \subseteq N$. For game $(N,v) \in {\mathcal {G}}$ and scalar , the game (N, c v) is given by $(c v)(S)=c \cdot v(S)$ for all $S \subseteq N$. The null game $(N,v^0)$ is given by $v^0(S) = 0$ for every $S \subseteq N$. For each $R\subseteq N$, $R \ne \emptyset$, the unanimity game $(N,u^{R})$ is given by $u^{R}(S)=1$ if $R\subseteq S$, and $u^{R}(S)=0$ otherwise. It is well known that for every game $(N,v) \in {\mathcal {G}}$ it holds that $v=\sum _{\emptyset \ne R \subseteq N}~\Delta _{v}(R)u^{R}$, i.e., v is a linear combination of the unanimity games, where the coefficients $\Delta _{v}(R)$ are the Harsanyi dividends, see Harsanyi (1959).

A payoff vector of TU-game (N, v) is a vector giving a payoff to any player $i \in N$. A (single-valued) solution for TU-games is a function f that assigns to every game $(N,v) \in {\mathcal {G}}$ a payoff vector . The best-known solution is the Shapley value (Shapley 1953), denoted by Sh. This value distributes the dividends of every coalition T uniformly among the members of T, thus

$$\begin{aligned} Sh_i(N,v) = \sum \limits _{T \subseteq N:i \in T} \frac{\Delta _v(T)}{|T|},~~~~i \in N. \end{aligned}$$

2.2 Digraphs

A directed graph or digraph is a pair (N, D), where N is a set of nodes and the collection of ordered pairs $D \subseteq \{(i,j)|i,j \in N, i \ne j\}$ is a set of arcs. In this paper the nodes represent the players in a game. We denote the set of all digraphs by ${\mathcal {D}}$.

For $S \subseteq N$, the digraph (S, D(S)) with $D(S)=\{(i,j) \in D|i,j\in S\}$ is called the subgraph of D on S. For $i\in N$, the nodes in $F_D(i):=\{j\in N\mid (i,j)\in D\}$ are called the followers of i, and the nodes in $P_D(i):=\{j\in N\mid (j,i)\in D\}$ are called the predecessors of i. For $S \subseteq N$, we denote $F_D(S) = \bigcup _{i \in S} F_D(i)$ and $P_D(S) = \bigcup _{i \in S} P_D(i)$. Given $(N,D) \in {\mathcal {D}}$, a sequence of k different players $(i_1,\ldots ,i_k)$ is a (directed) path if $(i_l,i_{l+1})\in D$ for $l=1,\ldots ,k-1$. The transitive closure of $(N,D) \in {\mathcal {D}}$ is the digraph (N, tr(D)) where for any pair $i,j \in N, i \ne j$, it holds that $(i,j) \in tr(D)$ if and only if there is a directed path from i to j. We refer to the players in $\widehat{F}_D(i)=F_{tr(D)}(i)$ as the subordinates of i and to the players in $\widehat{P}_D(i) = \{j \in N \mid i \in \widehat{F}_D(j)\}$ as the superiors of i. Also, for $S \subseteq N$, we denote $\widehat{F}_D(S) = \cup _{i \in S}~\widehat{F}_D(i)$ and $\widehat{P}_D(S) = \cup _{i \in S}~\widehat{P}_D(i)$.

In a digraph (N, D) player $i \in N$ is called top player when ${P}_D(i) = \emptyset$. A digraph (N, D) is a rooted tree with root i when (i) player i is the unique top player and (ii) for each $j \ne i$ there is a unique directed path from i to j. Note that this implies that $|P_D(j)| = 1$ for all $j \ne i$. In the sequel we denote by ${\mathcal {D}}_{t}$ the class of directed rooted trees and an element of ${\mathcal {D}}_t$ by (N, T). We denote the unique top player in (N, T) by Top(N, T).

2.3 Permission tree games

A game with a permission structure is a triple (N, v, D) with $N \subset {\mathbb N}$ a finite set of players, $(N,v) \in {\mathcal {G}}$ a TU-game and $(N,D) \in {\mathcal {D}}$ a digraph on N. In those games it is assumed that the players are organized in a hierarchy given by the directed graph. The hierarchy imposes restrictions on the forming of coalitions. In the conjunctive approach to permission structures as developed in Gilles et al. (1992) and van den Brink and Gilles (1996), a coalition is feasible if and only if for every player in the coalition all its predecessors are also in the coalition. In the disjunctive approach developed in Gilles and Owen (1994) and van den Brink (1997), a coalition is feasible if and only if for every non-top player in the coalition at least one of its predecessors is also in the coalition. In this paper we only consider triples (N, v, T) with the permission structure $(N,T) \in {\mathcal {D}}_t$ a rooted tree. We denote by ${\mathcal {G}}_{\mathcal {T}}$ the collection of all (N, v, T) with (N, T) a rooted tree and refer to these games as permission tree games. A (single-valued) solution f on ${\mathcal {G}}_{\mathcal {T}}$ assigns a unique payoff vector $f(N,v,T) \in {\mathbb R}^N$ to every $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$.

On the class ${\mathcal {G}}_{\mathcal {T}}$ the conjunctive and disjunctive approaches coincide and for a tree (N, T) the set of feasible coalitions is given by

$$\begin{aligned} \Phi _T = \left\{ S \subseteq N \left| P_T(i) \subseteq S \text{ for } \text{ all } i \in S \right. \right\} . \end{aligned}$$

For $S \subseteq N$, let $\sigma _T(S) = \bigcup _{R \in \Phi _T: R \subseteq S} R$ be the largest feasible subset³ of S. Following the references above, the induced permission restricted game of (N, v, T) is the game $(N,r_{N,v,T}) \in {\mathcal {G}}$ given by

$$\begin{aligned} r_{N,v,T} (S) = v(\sigma _T(S))\quad \text{ for } \text{ all } S \subseteq N, \end{aligned}$$

(2.1)

and the permission value $\varphi$ on ${\mathcal {G}}_{\mathcal {T}}$ is the solution that assigns to each (N, v, T) the Shapley value of the associated permission restricted game, thus

3 Three new solutions for permission tree games

In this section we define three solutions for permission tree games. The first one is the Myerson value. This value has been introduced by Myerson (1977) for communication graph games. A communication graph game is a triple (N, v, L) with (N, v) a TU-game and (N, L) an undirected (communication) graph, i.e., $L \subseteq \{\{i,j\}|i,j \in N, i \ne j\}$ is a collection of undirected pairs of two elements of N. The so-called Myerson restricted game of (N, v, L) is the TU-game $(N,v^L)$ given by

$$\begin{aligned} v^{L}(S)=\sum _{T\in C_{L}(S)}v(T) \text{ for } \text{ all } S \subseteq N, \end{aligned}$$

(3.1)

where $C_L(S)$ is the set of components of S in the subgraph (S, L(S)).⁴ So, $v^L(S) = v(S)$ when S is connected; otherwise, $v^L(S)$ is the sum of the worths of its components. The Myerson value $\mu$ on the class of communication graph games is defined by . For a directed rooted tree $(N,T) \in {\mathcal {D}}_{t}$, let $(N,L_T) \in {\mathcal {L}}$ be the corresponding undirected (connected and cycle-free) communication graph given by $L_T = \{\{i,j\}:(i,j) \in T \text{ or } (j,i) \in T\}$. The Myerson value for permission tree games now assigns to every permission tree game the Myerson value of the associated communication graph game.

Definition 3.1

The Myerson value for permission tree games is the solution $\mu$ given by

The second solution is the hierarchical outcome. On the class of cycle-free and connected communication graph games, Demange (2004) defined for each player $i \in N$ its corresponding hierarchical outcome. We define the hierarchical outcome for permission tree games as the solution that for every $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$ assigns the hierarchical outcome of $(N,L_T)$ with respect to the unique top player Top(N, T). We denote this solution by $\eta$.⁵

Definition 3.2

The hierarchical outcome for permission tree games is the solution $\eta$ given by

$$\begin{aligned} \eta _j(N,v,T) = v(\widehat{F}_T(j) \cup \{j\}) -\sum _{h \in F_T(j)} v(\widehat{F}_T(h) \cup \{h\}) \quad \hbox {for all} \, j \in N. \end{aligned}$$

Note that for each $j \in N$ it holds that $\sum _{h \in \widehat{F}_T(j) \cup \{j\}} \eta _j(N,v,T)= v(\widehat{F}_T(j) \cup \{j\})$, implying that $\eta _j(N,v,T) = v(\{j\})$ if $F_T(j) = \emptyset$.⁶

Third we introduce the top value as the solution that for every $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$ assigns the worth v(N) of the grand coalition N fully to the (unique) top player Top(N, T), while the other players get a payoff of zero. We denote this solution by $\tau$.

Definition 3.3

The top value for permission tree games is the solution $\tau$ given by

$$\begin{aligned} \tau _i(N,v,T) = \left\{ \begin{array}{l@{\quad }l} v(N) &{} \text{ if } \quad i =Top(N,T)\\ 0 &{} \text{ if } \quad i \ne Top(N,T) \end{array}\right\} \, \hbox {for all} \, (N,v,T) \in {\mathcal {G}}_{\mathcal {T}}. \end{aligned}$$

Note that for the permission restricted game $(N,r_{N,v,T})$ we have that $r_{N,v,T}(S) = 0$ for every $S \subseteq N \setminus \{Top(N,T)\}$. From this it follows that $\tau (N,v,T) = \eta (N,r_{N,v,T},T)$, i.e., the top value assigns to each (N, v, T) the hierarchical outcome of the permission tree game $(N,r_{N,v,T},T)$. Although the top value seems to be extreme, we show in the next section that it comes out ‘naturally’ by an axiomatic comparison with the other solutions.

In the remaining of this section, we give the four solutions in terms of the Harsanyi dividends of the underlying game (N, v). Given a tree $(N,T) \in {\mathcal {D}}_{t}$, the connected hull of a coalition $R\subseteq N$, denoted by $\gamma _T(R)$, is defined as $\gamma _T(R) = \cap _{R \subseteq H \subseteq N:(H,T(H)) \in {\mathcal {D}}_{t}} H$, i.e., it is the smallest subtree in (N, T) containing R. The permission hull of R, denoted by $\alpha _T(R)$, is defined as $\alpha _T(R) = R \cup \widehat{P}_T(R)$, i.e., it is the smallest coalition in $\Phi _T$ containing R.⁷ Then we have the following results.

Proposition 3.4

• 1. The Myerson value $\mu$ can be written in terms of dividends as

  $$\begin{aligned} \mu _i(N,v,T) = \sum \limits _{R \subseteq N:i \in \gamma _T(R)} \frac{\Delta _{v}(R)}{|\gamma _T(R)|} \, \mathrm{for \, all} \, (N,v,T) \in {\mathcal {G}}_{\mathcal {T}} \, \mathrm{and} \, i \in N. \end{aligned}$$

• 2. The hierarchical outcome $\eta$ can be written in terms of dividends as

  $$\begin{aligned} \eta _i(N,v,T) = \sum \limits _{R \subseteq N: i = Top(\gamma _T(R),T(\gamma _T(R))}~\Delta _{v}(R) \, \mathrm{for \, all} \, (N,v,T) \in {\mathcal {G}}_{\mathcal {T}} \, \mathrm{and} \, i \in N. \end{aligned}$$

• 3. The top value $\tau$ can be written in terms of dividends as

  $$\begin{aligned} \tau _i(N,v,T) = \left\{ \begin{array}{ll} \sum \limits _{R \subseteq N:R \ne \emptyset } \Delta _{v}(R) &{} \, \mathrm{if} \quad i =Top(N,T) \\ 0 &{} \, \mathrm{if} \quad i \ne Top(N,T) \end{array}\right\} \, \mathrm{for \, all} \, (N,v,T) \in {\mathcal {G}}_{\mathcal {T}}. \end{aligned}$$

• 4. The permission value $\varphi$ can be written in terms of dividends as:

  $$\begin{aligned} \varphi _i(N,v,T) = \sum \limits _{R \subseteq N: i \in \alpha _T(R)} \frac{\Delta _{v}(R)}{|\alpha _T(R)|} \, \mathrm{for \, all} \, (N,v,T) \in {\mathcal {G}}_{\mathcal {T}} \quad \mathrm{and} \quad i \in N. \end{aligned}$$

This proposition shows that the Myerson value allocates the dividend of a coalition R equally over the players in the connected hull of R. This result follows from Owen (1986). The hierarchical outcome assigns the dividend of a coalition R exclusively to the top player in the subtree on the connected hull of R. This follows straightforward from rewriting the expression of the hierarchical outcome in terms of dividends. The top value assigns the dividend of a coalition R exclusively to the top player in the subtree on the permission hull of R, which is always the top player of the tree itself. This follows from the fact that $v(N) = \sum _{\emptyset \ne S \subseteq N}~\Delta _{v}(S)$. The permission value allocates the dividend of a coalition R equally over the players in the permission hull of R. From Gilles et al. (1992), it is known that the dividend of R in the permission restricted game $r_{N,v,T}$ is given by $\sum _{\emptyset \ne S \subseteq R:R = \alpha _T(S)} \Delta _{v}(S)$. Then the result follows from the fact that $\varphi (N,v,T) = Sh(N,r_{N,v,T})$.

Example 3.5

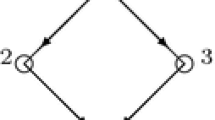
We illustrate the four solutions with the permission tree game (N, v, T) with $N=\{1,2,3,4,5\}$, $v=u^{\{4,5\}}$ the unanimity game on coalition $\{4,5\}$, and $D=\{(1,2),(1,3),(3,4),(3,5)\}$ as illustrated in Fig. 1.

The permission value allocates the dividend of coalition $\{4,5\}$ equally over the players in the set $\alpha _T(\{4,5\}) = \{1,3,4,5\}$, giving $\varphi (N,v,D) = (\frac{1}{4},0,\frac{1}{4}, \frac{1}{4}, \frac{1}{4})$. The Myerson value allocates the dividend of coalition $\{4,5\}$ equally over the players in the set $\gamma _T(\{4,5\}) = \{3,4,5\}$, giving $\mu (N,v,D) = (0,0,\frac{1}{3}, \frac{1}{3}, \frac{1}{3})$. The hierarchical outcome assigns the dividend fully to the unique ‘highest’ connecting player 3, giving $h(N,v,D) = (0,0,1,0,0)$. Finally, the top value gives the dividend fully to the unique top player 1, giving $\tau (N,v,D)=(1,0,0,0,0)$.

Fig. 1

Permission tree (N, T) of example 3.5

4 Characterization of four solutions for permission tree games

In this section, we provide comparable axiomatizations of the three solutions introduced in the previous section and the permission value. We first state the axioms for a solution f on the class of permission tree games that will be used in characterizing the four solutions. The first two axioms are standard. Efficiency states that the payoffs assigned to players must sum to v(N), the worth of the grand coalition. Additivity states that the solution applied to the sum of two permission tree games on the same permission tree (N, T) gives the same payoff vector as the sum of two payoff vectors obtained when applying the solution to each of the two permission tree games.

Efficiency For every $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$, it holds that $\sum _{i \in N} f_i(N,v,T) = v(N)$.

Additivity For every $(N,v,T), (N,w,T) \in {\mathcal {G}}_{\mathcal {T}}$, it holds that $f(N,v+w,T) = f(N,v,T) + f(N,w,T)$.

A player $i \in N$ is a pending null player in $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$ if it is both a null player in game (N, v) (meaning that $v(S \cup \{i\}) = v(S)$ for all $S \subseteq N \setminus \{i\}$) and a pending player in the undirected communication graph $(N,L_T)$ (meaning there exists only one player $j \in N$ such that $\{i,j\} \in L_T$). Notice that in tree (N, T), player i is a pending player if i has no followers. Further, the top player is a pending player if and only if it has only one follower. Notice that when i is pending on rooted tree (N, T), then also the subgraph $(N_{-i},T_{-i})$ is a rooted tree, where $(N_{-i},T_{-i})$ denotes the subtree $(N_{-i}, T(N_{-i}))$. The pending null player out property states that pending null players can be removed from the permission tree game without affecting the payoff distribution of the other players. The weak version only requires this for those pending null players that are not the top player.⁸ Let $(N_{-i},v_{-i},T_{-i})$ denote the permission tree game given by the subgame $(N_{-i},v_{-i})$ of (N, v) on the subtree $(N_{-i},T_{-i})$ of (N, T).

Pending null player out property For every $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$, when i is a pending null player in (N, v, T), it holds that $f_j(N,v,T) = f_j(N_{-i},v_{-i},T_{-i})$ for all $j \in N_{-i}$.

Weak pending null player out property For every $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$, when $i \in N \setminus \{Top(N,T)\}$ is a pending null player in (N, v, T), it holds that $f_j(N,v,T) = f_j(N_{-i},v_{-i},T_{-i})$ for $j \in N_{-i}$.

A player $i \in N$ is said to veto player $j \in N$ in game (N, v) if $v(S \cup \{j\}) - v(S) = 0$ for any coalition $S \subseteq N_{-i}$. Let $(N,v^i_j)$ be the game derived from (N, v) when player i vetoes player j, i.e.,

$$\begin{aligned} v^i_j(S) = \left\{ \begin{array}{ll} v(S \setminus \{j\}) &{} \text{ if } \quad i \not \in S\\ v(S) &{} \text{ if } \quad i \in S. \end{array}\right. \end{aligned}$$

When player i vetoes player j in this way, then the dividend of a coalition R in game (N, v) such that $i \notin R$ and $j \in R$ is shifted to that of coalition $R \cup \{i\}$ in game $(N,v^i_j)$. We therefore have the following expression:

$$\begin{aligned} v^i_j = v +\sum \limits _{R \subseteq N: j \in R} \Delta _{v}(R)[u^{R \cup \{i\}}- u^R]. \end{aligned}$$

(4.1)

Predecessor necessity⁹ states that the payoff distribution does not change if for a ordered pair $(i,j) \in T$ the game (N, v) is replaced by the game $(N,v^i_j)$, i.e., if predecessor i is going to veto follower j. The weak version only requires that the payoff distribution does not change when i is going to veto his follower j in the game $(N,v^i_j)$ when in the game (N, v) the marginal contribution of player j to any coalition that is a subset of his subordinates is zero.

Predecessor necessity For every $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$ and $i, j \in N$ such that $(i,j) \in T$, it holds that $f(N,v,T) = f(N,v^i_j,T)$.

Weak predecessor necessity For every $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$ such that $(i,j) \in T$ and $v(S \cup \{j\})-v(S) = 0$ for all $S \subseteq \widehat{F}_T(j)$, it holds that $f(N,v,T) = f(N,v^i_j,T)$.

A player $i\in N$ is called necessary in game (N, v) if $v(S) = 0$ for all $S \subseteq N \setminus \{i\}$. The next two axioms are restricted to monotone games where all players are necessary. In that case the players are symmetric in the game, but still differ by their position in the permission tree. For such games the next two axioms reflect extreme ways of how to handle payoff allocations. The necessary player symmetry axiom requires that all players get the same payoff¹⁰ and so reflects a full egalitarian approach. The one-player property requires the counterpart that there is at most one player that gets a nonzero payoff. Together with efficiency, this implies that the full payoff goes to precisely one player, expressing the most unequal approach.

Necessary player symmetry For every $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$ with (N, v) monotone and all players necessary, $f_i(N,v,T) = f_j(N,v,T) \, \text{ for } \text{ all } i,j \in N$.

One-player property For every $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$ with (N, v) monotone and all players necessary, there is at most one player $j \in N$ such that $f_j(N,v,T) \ne 0$.

The last axiom is structural monotonicity. It states that when there is a necessary player in a monotone game (N, v), then such a player gets at least the same payoff as each of its subordinates.¹¹

Structural monotonicity For every $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$ such that (N, v) is monotone, if $i \in N$ is a necessary player in (N, v), then $f_i(N,v,T) \ge f_j(N,v,T)$ for all $j \in \widehat{F}_{T}(i)$.

Before giving the characterizations of the four solutions, we first state a proposition that will be used.

Proposition 4.1

Let $\emptyset \ne R \subseteq N$ and . Then

• (i) For any solution f on the class ${\mathcal {G}}_{\mathcal {T}}$ satisfying efficiency and the pending null player out property, it holds that $f_i(N,cu^R,T) = 0$ if $i \in N \setminus \gamma _T(R)$, and $f_i(N,cu^R,T)= f_i(\gamma _T(R),(cu^R)_{\gamma _T(R)},T(\gamma _T(R)))$ for $i \in \gamma _T(R)$.

• (ii) For any solution f satisfying efficiency and the weak pending null player out property, it holds that $f_i(N,cu^R,T) = 0$ if $i \in N \setminus \alpha _T(R)$, and $f_i(N,cu^R,T)= f_i(\alpha _T(R),(cu^R)_{\alpha _T(R)},T(\alpha _T(R)))$ for $i \in \alpha _T(R)$.

• (iii) For any solution f satisfying predecessor necessity, it holds that $f(N,cu^R,T) = f(N,cu^{\alpha _T(R)},T)$.

• (iv) For any solution f satisfying weak predecessor necessity, it holds that $f(N,cu^R,T) = f(N,cu^{\gamma _T(R)},T)$.

Proof

Consider any permission tree game $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$. For any player $i \in N$ being a null player in (N, v) we have $v(N)=v(N_{-i})=v_{N_{-i}}(N_{-i})$.

(i) Let $i \in N$ be a pending null player. Therefore i is a null player. By efficiency it holds that $\sum _{j \in N_{-i}} f_j(N_{-i},v_{-i},T_{-i}) = v_{-i}(N_{-i}) = v(N)$. By efficiency it also holds that $\sum _{j \in N} f_j(N,v,T) = v(N)$. By the pending null player out property, it holds that $f_j(N,v,T) = f_j(N_{-i},v_{-i},T_{-i})$ for $j \in N_{-i}$. Therefore $\sum _{j \in N_{-i}} f_j(N,v,T) = v(N)$ and thus $f_i(N,v,T) = 0$. By repeated application of the pending null player out property and efficiency in this way, it follows that $f_i(N,cu^R,T) = 0$ if $i \in N \setminus \gamma _T(R)$ and $f_i(N,cu^R,T)=f_i(\gamma _T(R),(cu^R)_{\gamma _T(R)},T(\gamma _T(R)))$ for $i \in \gamma _T(R)$.

(ii) It is similar to the proof of (i), but applies the weak pending null player out property only for pending players that do not have followers.

(iii) and (iv) The proofs follow straightforwardly from repeated application of predecessor necessity and weak predecessor necessity, respectively. $\square$

In the next four theorems, we characterize each of the four values by a subset of the nine axioms given above. For each of the four theorems, the logical independence of the used axioms is shown in the Appendix. We first characterize the Myerson value on the class of permission tree games.

Theorem 4.2

A solution on ${\mathcal {G}}_{\mathcal {T}}$ is equal to the Myerson value $\mu$ if and only if it satisfies efficiency, additivity, the pending null player out property, weak predecessor necessity and necessary player symmetry.

Proof

It is straightforward to verify that the Myerson value satisfies efficiency, additivity, the pending null player out property and necessary player symmetry.

To show that the Myerson value satisfies weak predecessor necessity, we argue as follows. By Proposition 3.4, $\mu _k(N,v,T) = \sum _{R \subseteq N:k \in \gamma _T(R)} \frac{\Delta _{v}(R)}{|\gamma _T(R)|} \text{ for } \text{ all } k \in N$. Consider those coalitions R such that $j \in R$ and $i \notin R$, $(i,j) \in T$. Denote by ${\mathcal {V}}$ the collection of these coalitions R such that $j \in R$ and $i \in \gamma _T(R)$. For $R \in {\mathcal {V}}$ it holds that $\gamma _T(R) = \gamma _T(R \cup \{i\})$. Denote by ${\mathcal {W}}$ the collection of those coalitions R such that $j \in R$ and $i \notin \gamma _T(R)$. By Proposition 3.4 and Eq. (4.1), $\mu _k(N,v^i_j,T) = \sum _{R \subseteq N:k \in \gamma _T(R)} \frac{\Delta _{v^i_j}(R)}{|\gamma _T(R)|} = \sum _{R \in 2^N\setminus ({\mathcal {V}} \cup {\mathcal {W}}): k \in \gamma _T(R)} \frac{\Delta _{v}(R)}{|\gamma _T(R)|} + \sum _{R \in {\mathcal {V}}: k \in \gamma _T(R\cup \{i\})} \frac{\Delta _{v}(R)}{|\gamma _T(R\cup \{i\})|} +\sum _{R \in {\mathcal {W}}: k \in \gamma _T(R\cup \{i\})} \frac{\Delta _{v}(R)}{|\gamma _T(R\cup \{i\})|} = \sum _{R \in 2^N \setminus {\mathcal {W}}:k \in \gamma _T(R)}\frac{\Delta _{v}(R)}{|\gamma _T(R)|} + \sum _{R \in {\mathcal {W}}: k \in \gamma _T(R\cup \{i\})} \frac{\Delta _{v}(R)}{|\gamma _T(R\cup \{i\})|}$ for all $k \in N$. Let $R \in {\mathcal {W}}$, i.e., $j \in R$ and $i \not \in \gamma _T(R)$. Since $(i,j) \in T$, we have that $R \subseteq \widehat{F}_T(j) \cup \{j\}$. If $v(S \cup \{j\}) - v(S) = 0$ for all $S \subseteq \widehat{F}(j)$, then we have $\Delta _v(R) = 0$. We obtain $\mu (N,v,T)=\mu (N,v^i_j,T)$, showing that the Myerson value satisfies weak predecessor necessity.

To prove uniqueness, let f be a solution satisfying the axioms. For some $c > 0$, first we consider the permission tree game $(N,cu^R,T)$ for a coalition R connected in the underlying undirected communication graph $(N,L_T)$, so $R = \gamma _T(R)$. By Proposition 4.1.(i) and f satisfying efficiency and the pending null player out property, (i) the players in $N \setminus \gamma _T(R) = N \setminus R$ obtain a payoff of 0, and (ii) $f_i(N,cu^R,T)=f_i(R,cu^R,T(R))$ for all $i \in R$. By efficiency the players in R together obtain $cu^R(R) =cu^R(N)=c$. Since the players in R are all necessary players in $(R,cu^R,T(R))$ and $cu^R$ is monotone (because $c > 0$), necessary player symmetry implies that $f_i(R,cu^R,T(R)) = \frac{c}{|R|}$ for all $i \in R$. Since $f_i(N,cu^R,T)=f_i(R,cu^R,T(R))$ for all $i \in R$, $f(N,cu^R,T)$ is uniquely determined for $c > 0$ and R connected in $(N,L_T)$.

Now, for some $c > 0$, consider any coalition R not connected in $(N,L_T)$, so $R \ne \gamma _T(R)$. By Proposition 4.1.(iv) and f satisfying weak predecessor necessity, it holds that $f(N,cu^R,T)=f(N,cu^{\gamma _T(R)},T)$. Since $\gamma _T(R)$ is a connected coalition in $(N,L_T)$, $f(N,cu^{\gamma _T(R)},T)$ has been uniquely determined above and therefore also $f(N,cu^R,T)$ is uniquely determined.

Consider the permission tree game $(N,v^0,T)$, with $(N,v^0)$ the null game. By additivity and the fact that $v^0 = v^0 + v^0$, we have $f(N,v^0,T) = f(N,v^0 + v^0,T) = f(N,v^0,T) + f(N,v^0,T)$, and therefore $f_i(N,v^0,T)=0$ for all $i \in N$. Next, consider $(N,cu^R,T)$ for some $c<0$. Since $v^0 = cu^R + (-cu^R)$, it follows from additivity of f that $f(N,cu^R, T) = f(N,v^0,T) - f(N,-cu^R,T) = -f (N,-cu^R,T)$ is uniquely determined above because $-c>0$, and thus $(N,-c u^R)$ is monotone.

Finally, since for every $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$ it holds that v can be written as $v=\sum _{\emptyset \ne R \subseteq N} \Delta _v(R) u^R$, additivity uniquely determines $f(N,v,T) = \sum _{\emptyset \ne R \subseteq N} f(N,\Delta _v(R) u^R,T)$ for any $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$. $\square$

The hierarchical outcome satisfies all axioms in the above theorem except necessary player symmetry. We obtain a characterization of the hierarchical outcome for permission tree games by replacing necessary player symmetry by the one-player property and structural monotonicity. Note that the pending null player out property and necessary player symmetry together imply structural monotonicity, so also the Myerson value satisfies structural monotonicity.

Theorem 4.3

A solution on ${\mathcal {G}}_{\mathcal {T}}$ is equal to the hierarchical outcome $\eta$ if and only if it satisfies efficiency, additivity, the pending null player out property, weak predecessor necessity, structural monotonicity and the one-player property.

Proof

It is straightforward to verify that the hierarchical outcome satisfies efficiency, additivity, the pending null player out property, structural monotonicity and the one-player property. By arguments similar to the proof that the Myerson value satisfies weak predecessor necessity, it follows that the hierarchical outcome satisfies weak predecessor necessity.

To prove uniqueness, let f be a solution satisfying the axioms. For some $c>0$, again first we consider the permission tree game $(N,cu^R,T)$ for a coalition R connected in the underlying undirected communication graph $(N,L_T)$, so $R = \gamma _T(R)$. By Proposition 4.1.(i) and f satisfying efficiency and the pending null player out property, we obtain that (i) the players in $N \setminus \gamma _T(R) = N \setminus R$ obtain a payoff of 0, and (ii) $f_i(N,cu^R,T)=f_i(R,(cu^R)_R,T(R))$ for $i \in R$. Since in $(R,(cu^R)_R)$ all players are necessary, we can apply the one player property to obtain that there is only one player $j \in R$ such that $f_j(R,(cu^R)_R,T(R)) \ne 0$. Let $r_0=Top(R,R(T))$ be the top player in the subtree (R, T(R)). Since (i) $r_0$ is a necessary player in $(R,(cu^R)_R)$, (ii) every $j \in R \setminus \{r_0\}$ is a subordinate of $r_0$ in (R, T(R)), and (iii) $cu^R$ is monotone (because $c > 0$), structural monotonicity implies that $f_{r_0}(R,(cu^R)_R,T(R)) \ge f_j(R,(cu^R)_R,T(R))$ for all $j \in R \setminus \{r_0\}$. So, the one-player property, structural monotonicity and efficiency imply that $f_{r_0}(R,(cu^R)_R,T(R)) = c$ and $f_j(R,(cu^R)_R,T(R))=0$ for all $j \in R \setminus \{r_0\}$. Therefore $f(N,cu^R,T)$ is uniquely determined.

The cases (i) $R \ne \gamma _T(R)$ and $c>0$, (ii) $c<0$ and (iii) $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$ follow along similar lines to those in the proof of Theorem 4.2 for the Myerson value. $\square$

From the axioms used in Theorem 4.3, the top value satisfies all except the pending null player out property. The top value is characterized by replacing the pending null player out property by the weak pending null player out property and by replacing weak predecessor necessity by predecessor necessity.

Theorem 4.4

A solution on ${\mathcal {G}}_{\mathcal {T}}$ is equal to the top value $\tau$ if and only if it satisfies efficiency, additivity, the weak pending null player out property, predecessor necessity, structural monotonicity and the one-player property.

Proof

It is straightforward to verify that the top value satisfies efficiency, additivity, the weak pending null player out property, structural monotonicity and the one-player property. The top value satisfying predecessor necessity follows from $v^i_j (N)=v(N)$ and the fact that for any two games (N, v, T) and $(N,v',T)$ such that $v(N)=v'(N)$ it holds that $\tau (N,v,T)=\tau (N,v',T)$.

To prove uniqueness, let f be a solution satisfying the axioms. For some $c>0$, first we consider the permission tree game $(N,cu^R,T)$ for a coalition R with R having full permission in T, so R is equal to the permission hull $\alpha _T(R)$. By Proposition 4.1.(ii) and f satisfying efficiency and the weak pending null player out property, we obtain that (i) the players in $N \setminus \alpha _T(R) = N \setminus R$ obtain a payoff of 0, and (ii) $f_i(N,cu^R,T)=f_i(R,(cu^R)_R,T(R))$ for $i \in R$. Since all players in the game $(R,(cu^R)_R)$ are necessary, we can apply the one-player property to obtain that there is only one player $j \in R$ such that $f_j(R,(cu^R)_R,T(R)) \ne 0$. Let $i_0=Top(N,T)$. Since (i) $i_0 \in R$ (because $R = \alpha _T(R)$), (ii) $i_0$ is necessary in $(R,(cu^R)_R)$, (iii) every $j \in R \setminus \{i_0\}$ is a subordinate of $r_0$ in (R, T(R)), and (iv) $cu^R$ is monotone (because $c > 0$), structural monotonicity implies that $f_{i_0}(R,(cu^R)_R,T(R)) \ge f_j(R,(cu^R)_R,T(R))$ for all $j \in R \setminus \{i_0\}$. So, the one-player property, structural monotonicity and efficiency imply that $f_{i_0}(R,(cu^R)_R,T(R)) = c$ and $f_j(R,(cu^R)_R,T(R))=0$ for all $j \in R \setminus \{i_0\}$. Therefore, $f(N,cu^R,T)$ is uniquely determined.

Next, consider those coalitions R that do not have full permission in (N, T), so $R \ne \alpha _T(R)$. By Proposition 4.1.(iv) and f satisfying predecessor necessity, it holds that $f(N,cu^R,T)=f(N,cu^{\alpha _T(R)},T)$. Since $\alpha _T(R)$ has full permission in (N, T), $f(N,cu^{\alpha _T(R)},T)$ has been uniquely determined above, and therefore, also $f(N,cu^R,T)$ is uniquely determined.

The cases $c<0$ and $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$ follow along similar lines to those in the proof of Theorem 4.2 for the Myerson value. $\square$

Finally, it turns out that the permission value is characterized by replacing the one-player property in the characterization of the top value by necessary player symmetry. Further structural monotonicity can be deleted, since the weak pending null player out property, predecessor necessity and necessary player symmetry together imply structural monotonicity.

Theorem 4.5

A solution on ${\mathcal {G}}_{\mathcal {T}}$ is equal to the permission value $\varphi$ if and only if it satisfies efficiency, additivity, the weak pending null player out property, predecessor necessity and necessary player symmetry.

Proof

The permission value satisfying efficiency, additivity and necessary player symmetry follows from van den Brink and Gilles (1996),¹² $\varphi$ satisfying predecessor necessity follows from van den Brink et al. (2015), and it is straightforward to show that $\varphi$ satisfies the weak pending null player out property.

To prove uniqueness, let f be a solution satisfying the axioms. For some $c>0$, first we consider the permission tree game $(N,cu^R,T)$ for a coalition R with $R = \alpha _T(R)$, implying that top player $i_0 \in R$. By Proposition 4.1.(ii) and f satisfying efficiency and the weak pending null player out property, we obtain that (i) the players in $N \setminus \alpha _T(R) = N \setminus R$ obtain a payoff of 0, and (ii) $f_i(N,cu^R,T) = f_i(R,cu^R,T(R))$ for all $i \in R$. By efficiency, the players in R obtain $cu^R(N)=c$. Since all players in R are necessary and $cu^R$ is monotone, necessary player symmetry implies that $f_i(R,cu^R,T(R)) = \frac{c}{|R|}$ for every $i \in R$. Since $f_i(N,cu^R,T)=f_i(R,cu^R,T(R))$ for all $i \in R$, $f(N,cu^R,T)$ is uniquely determined for $c > 0$ and coalition R with $R = \alpha _T(R)$.

Now consider those coalitions R that do not have full permission in (N, T), so $R \ne \alpha _T(R)$. By Proposition 4.1.(iv) and f satisfying predecessor necessity, it holds that $f(N,cu^R,T)=f(N,cu^{\alpha _T(R)},T)$. Since $\alpha _T(R)$ has full permission in (N, T), $f(N,cu^{\alpha _T(R)},T)$ has been uniquely determined above, and therefore, also $f(N,cu^R,T)$ is uniquely determined.

The cases $c<0$ and $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$ follow along similar lines to those in the proof of Theorem 4.2 for the Myerson value. $\square$

5 Comparing the four solutions

Table 1 gives an overview of the axioms used to characterize the four solutions for permission tree games (those marked with a ++). Moreover, it shows which other axioms are satisfied by the solutions (those marked with a +). In all four axiomatizations, we use the first two axioms: efficiency and additivity. All four solutions also satisfy the next three axioms (second part of Table 1): the weak pending null player out property, weak predecessor necessity and structural monotonicity. Although not appearing explicitly in all axiomatizations, the weak pending null player out property and weak predecessor necessity appear implicitly in all axiomatizations since the two axiomatizations that do not use the weak pending null player out property use the stronger pending null player out property, and the two axiomatizations that do not use weak predecessor necessity use the stronger predecessor necessity. Also structural monotonicity is satisfied by all solutions, because for the Myerson value structural monotonicity is implied by necessary player symmetry, the pending null player out property and efficiency, and for the permission value structural monotonicity is implied by necessary player symmetry, predecessor necessity, the weak pending null player out property and efficiency. The four solutions are distinguished by the last four axioms in the table. Each of the four solutions satisfies exactly two of the final four axioms in the table, and together with the previous axioms, these give an axiomatization of the corresponding solution. Moreover, each of these four axioms appears in precisely two axiomatizations.

Table 1 Axioms satisfied by the four solutions

In the axiomatizations, we used four of six combinations containing two out of these last four axioms. This leaves two combinations that have not been considered. It turns out that these two combinations of two out of four axioms are incompatible with the other axioms. In other words, a solution satisfying efficiency, additivity, the weak pending null player out property and weak predecessor necessity cannot also satisfy both the pending null player out property and predecessor necessity nor satisfy both necessary player symmetry and the one-player property.

Proposition 5.1

There does not exist a solution f satisfying efficiency, additivity, the pending null player out property, structural monotonicity and predecessor necessity.

Proof

Consider a permission tree game $(N,u^{\{i\}},T)$, where $|N|>1$ and $(N,u^{\{i\}})$ is the unanimity game of a player $i \ne Top(N,T)$. By Proposition 4.1.(i) and f satisfying efficiency and the pending null player out property, it holds that $f_j(N,u^{\{i\}},T) = 0$ for $j \in N \setminus \{i\}$, and $f_i(N,u^{\{i\}},T) = u^{\{i\}}(N)=1$. By repeatedly applying predecessor necessity, we also obtain that $f(N,u^{\{i\}},T) = f(N,u^{\alpha _T(i)},T)$. According to structural monotonicity, it holds that $1=f_i(N,u^{\{i\}},T) = f_i(N,u^{\alpha _T(i)},T) \le f_j(N,u^{\alpha _T(i)},T) = f_j(N,u^{\{i\}},T)=0$ for $j \in \widehat{P}_T(i)$. Since $\widehat{P}_T(i) \ne \emptyset$, we obtain a contradiction and f cannot exist. $\square$

Proposition 5.2

There does not exist a solution f satisfying efficiency, additivity, the weak pending null player out property, necessary player symmetry, weak predecessor necessity and the one-player property.

Proof

For $|N| > 1$, consider a permission tree game $(N,u^{N},T)$. According to the one-player property, only one player can have a payoff that is nonzero. Efficiency implies that the payoff to this player must be $u^{N}(N)=1$. However, necessary player symmetry implies that $f_i(N,u^{N},T) = f_j(N,u^{N},T)$ for any two players $i,j \in N$. Since in $u^{N}$ all players in N are necessary and $|N|>1$, we obtain a contradiction and f cannot exist. $\square$

In this way we have comparable axiomatizations of the four solutions for permission tree games. Next, we describe this comparison in more detail.

The pending null player out property is satisfied by the Myerson value and the hierarchical outcome. It implies that players who do not contribute anything in the game nor connect any contributing players obtain a zero payoff. This follows from the communication feature of these two solutions. The permission and top value may still grant such players a nonzero payoff, by domination of contributing followers. This follows from the hierarchical feature of these two solutions. This is also shown by these solutions satisfying predecessor necessity, whereas the Myerson value and hierarchical outcome do not. Therefore, the Myerson value and the hierarchical outcome may be thought of as ‘communication solutions,’ whereas the permission value and the top value might be considered ‘hierarchy solutions’ for permission tree games.

However, this does not imply that ‘bottom players’ will always obtain a higher payoff from a ‘communication value’ than from a ‘hierarchy value.’ For example, in a unanimity game $u^R$ with R containing at least two bottom players, every bottom player gets zero payoff according to the hierarchical outcome, but earns a positive payoff according to the permission value. The reason is that the hierarchical outcome satisfies the one-player property, which together with the other axioms assigns the full unanimity payoff to the ‘local’ top player in the connected coalition, i.e., the player in the coalition who is closest to the root, while the permission value assigns equal payoffs to player j and all of its superiors because it satisfies necessary player symmetry (together with the other axioms). In this sense, there is another distinction between the four solutions. On the one hand, the Myerson value and the permission value satisfy necessary player symmetry, equally distributing the dividend of a coalition among the players needed to make that coalition feasible. The hierarchical outcome and the top value on the other hand satisfy the one-player property, assigning the payoff of a coalition to the unique top player among the players needed to make that coalition feasible. We summarize this in Fig. 2.

Fig. 2

Solution classifications

The interpretation of these solutions with respect to the hierarchy can be looked at in the following way. The Myerson value and the hierarchical outcome take a more local approach to hierarchies; coalitions within the hierarchy have some sense of autonomy in that they can operate without needing their predecessors to sign off on everything they do. The permission value and the top value take a global approach to hierarchies; everything a coalition does, needs to be approved by players located at a higher position in the hierarchy. The Myerson value and the permission value interpret the players of any feasible coalition in the hierarchy to play an equally important role. They should therefore be rewarded equally. The hierarchical outcome and the top value interpret the (local or global) top player of any feasible coalition to be the one that is in control; therefore, this player should obtain all of the rewards. A related observation is that in case coalition R contains the top (root) player i in some permission tree T, then the permission hull $\alpha _T(R)$ of R coincides with the connected hull $\gamma _T(R)$ of R, implying that $\mu (N,u^R,T)=\varphi (N,u^R,T)$ and $\tau (N,u^R,T)=\eta (N,u^R,T)$.

Finally, we note that the local permission value, recently introduced in van den Brink and Dietz (2014), satisfies efficiency, additivity, the weak pending null player out property, necessary player symmetry and structural monotonicity and so has these five axioms in common with the Myerson value and the permission value. To illustrate the difference of this value with the other values, consider, for example, the permission tree game (N, v, T) on $N=\{1,2,3,4\}$ with $v=u^{\{3,4\}}$ the unanimity game on players 3 and 4, and $T=\{(1,2),(2,3),(3,4)\}$ the linear order on four players. The four values discussed in this paper, respectively, assign payoffs $\varphi (N,v,T)=(\frac{1}{4},\frac{1}{4},\frac{1}{4},\frac{1}{4})$, $\mu (N,v,T)=(0,0,\frac{1}{2},\frac{1}{2})$, $\eta (N,v,T)=(0,0,1,0)$ and $\tau (N,v,T)=(1,0,0,0)$. Whereas in the permission value the players 3 and 4 need permission of all their superiors implying that the worth 1 is divided among all players in the permission hull $\alpha (\{3,4\}) = N$, according to the local permission value players only need permission of their predecessors, so the players 3 and 4 need permission of player 2, but permission of player 1 is not needed. Consequently, the local permission value assigns to this permission tree game the payoff vector $(0,\frac{1}{3},\frac{1}{3},\frac{1}{3})$.

Appendix: Logical independence of the axioms of the theorems in Sect. 4

Logical independence of the five axioms stated in Theorem 4.2 is shown by the following alternative solutions for permission tree games.

• 1. The solution $f_i(N,v,T)=0$, $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$, $i \in N$ satisfies additivity, the pending null player out property, weak predecessor necessity and necessary player symmetry. It does not satisfy efficiency.

• 2. For $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$ let Null(v) be the set of null players in v. Let f be the solution that for $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$ divides the worth v(N) of the grand coalition equally over all non-null players and the players that connect these players in the graph, and assigns a 0 payoff otherwise. So for $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$ solution f is given by $f_i(N,v,T)= \frac{v(N)}{|\gamma _T(N\backslash Null(v))|}$ for $i \in \gamma _T(N \backslash Null(v))$ and $f_i(N,v,T)=0$ for $i \in N \setminus \gamma _T(N \backslash Null(v))$. This solution satisfies efficiency, the pending null player out property, weak predecessor necessity and necessary player symmetry. It does not satisfy additivity.

• 3. The permission value satisfies efficiency, additivity, weak predecessor necessity and necessary player symmetry. It does not satisfy the pending null player out property.

• 4. The solution $f(N,v,T)=Sh(N,v)$, $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$ satisfies efficiency, additivity, the pending null player out property and necessary player symmetry. It does not satisfy weak predecessor necessity.

• 5. The hierarchical outcome satisfies efficiency, additivity, the pending null player out property and weak predecessor necessity. It does not satisfy necessary player symmetry.

Logical independence of the six axioms stated in Theorem 4.3 is shown by the following alternative solutions for permission tree games.

• 1. The solution $f_i(N,v,T)=0$, $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$, $i \in N$ satisfies additivity, the pending null player out property, weak predecessor necessity, structural monotonicity and the one-player property. It does not satisfy efficiency.

• 2. Consider the class of games (N, v, T), for which there is a coalition $R \subseteq N$ such that $\Delta _{v}(S) = 0$ if $\gamma _T(S) \ne R$. The solution that on this class of games assigns the hierarchical outcome and on games not in this class assigns the Myerson value satisfies efficiency, the pending null player out property, weak predecessor necessity, structural monotonicity and the one-player property. It does not satisfy additivity.

• 3. The top value satisfies efficiency, additivity, weak predecessor necessity, structural monotonicity and the one-player property. It does not satisfy the pending null player out property.

• 4. For a coalition S define $A(S)= (\gamma _T(S) \setminus (\widehat{F}_T(S) \cup S))$ to be those players in the connected hull $\gamma _T(S)$ that are not included in S nor are they subordinates of players in S. Now consider $f_i(N,v,T) = \sum _{i \in S\subseteq N:i = Top(\gamma _T(S),T(\gamma _T(S)))}$ $\Delta _{v}(S) + \sum _{\emptyset \ne S\subseteq N:i \in A(S), Top(\gamma _T(S),T(\gamma _T(S))) \notin S} \frac{\Delta _{v}(S)}{|A(S)|}\,i \in N$, $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$. This solution assigns the dividend of coalitions S, such that the top player of the connected hull $\gamma _T(S)$ is included in S uniquely to that top player and equally distributes the dividend of coalitions S not containing this top player over those players in the connected hull $\gamma _T(S)$ that are not included in S nor are they followers of players in S. This solution satisfies efficiency, additivity, the pending null player out property, structural monotonicity and the one-player property. It does not satisfy weak predecessor necessity.

• 5. For every coalition S, take any $r_T(S) \in F_T(Top(\gamma _T(S))) \cap \gamma _T(S)$ as a ‘representative’ of coalition S. Consider the solution $f_i(N,v,T)=\sum _{S \subseteq N : i=r_T(S)} \Delta _v(S)$ that assigns the dividend $\Delta _{v}(S)$ of a coalition S fully to this player $r_T(S)$. This solution satisfies efficiency, additivity, the pending null player out property, weak predecessor necessity and the one-player property. It does not satisfy structural monotonicity.

• 6. The Myerson value satisfies efficiency, additivity, the pending null player out property, weak predecessor necessity and structural monotonicity. It does not satisfy the one-player property.

Logical independence of the six axioms stated in Theorem 4.4 is shown by the following alternative solutions for permission tree games.

• 1. The solution $f_i(N,v,T)=0$, $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$, $i \in N$ satisfies additivity, the weak pending null player out property, predecessor necessity, structural monotonicity and the one-player property. It does not satisfy efficiency.

• 2. Let V be the class of games (N, v, T), for which there is a coalition $R \subseteq N$ such that $\Delta _{v}(S) = 0$ if $\alpha _T(S) \ne R$. The solution that on this class of games assigns the top value and on games not in this class assigns the permission value satisfies efficiency, the weak pending null player out property, predecessor necessity, structural monotonicity and the one-player property. It does not satisfy additivity.

• 3. Consider the solution that for $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$ assigns the dividend $\Delta _{v}(S)$ of coalitions S such that $\alpha _T(S)=N$ to Top(N, T) and distributes the dividend $\Delta _{v}(S)$ equally over N otherwise. This solution satisfies efficiency, additivity, predecessor necessity, structural monotonicity and the one-player property. It does not satisfy the weak pending null player out property.

• 4. The hierarchical outcome satisfies efficiency, additivity, the weak pending null player out property, structural monotonicity and the one-player property. It does not satisfy predecessor necessity.

• 5. For every coalition S, take any $r_T(S) \in F_T(Top(\alpha _T(S))) \cap \alpha _T(S)$ as a ‘representative’ of coalition S. Consider the solution $f_i(N,v,T)=\sum _{S \subseteq N : i=r_T(S)} \Delta _v(S)$ that assigns the dividend $\Delta _{v}(S)$ of a coalition S fully to this player $r_T(S)$. This solution satisfies efficiency, additivity, the weak pending null player out property, predecessor necessity and the one-player property. It does not satisfy structural monotonicity.

• 6. The permission value satisfies efficiency, additivity, the weak pending null player out property, predecessor necessity and structural monotonicity. It does not satisfy the one-player property.

Logical independence of the five axioms stated in Theorem 4.5 is shown by the following alternative solutions for permission tree games.

• 1. The solution $f_i(N,v,T)=0$, $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$, $i \in N$ satisfies additivity, the weak pending null player out property, weak predecessor necessity, structural monotonicity and the one-player property. It does not satisfy efficiency.

• 2. The solution that for $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$ equally divides the worth v(N) of the grand coalition over all non-null players and their predecessors in the graph and assigns a 0 payoff otherwise satisfies efficiency, the weak pending null player out property, predecessor necessity and necessary player symmetry. It does not satisfy additivity.

• 3. The solution that for $(N,v,T) \in {\mathcal {G}}_{\mathcal {T}}$ equally divides the worth v(N) of the grand coalition over the players in N satisfies efficiency, additivity, predecessor necessity and necessary player symmetry. It does not satisfy the weak pending null player out property.

• 4. The solution $f(N,v,T)=Sh(N,v)$ satisfies efficiency, additivity, the weak pending null player out property and necessary player symmetry. It does not satisfy predecessor necessity.

• 5. The top value satisfies efficiency, additivity, the weak pending null player out property and predecessor necessity. It does not satisfy necessary player symmetry.