Abstract
This paper considers incentives for information acquisition ahead of conflicts. First, we characterize the (unique) equilibrium of the all-pay auction between two players with one-sided asymmetric information where one player has private information about his valuation. Then, we use our results to study information acquisition prior to an all-pay auction. If the decision to acquire information is observable, but not the information received, one-sided asymmetric information can occur endogenously in equilibrium. Moreover, the cut-off values of the cost of information that determine equilibrium information acquisition are higher than those in the first best. Thus, information acquisition is excessive. In contrast, with open or covert information acquisition, the equilibrium cut-off values are as in the first best.


Similar content being viewed by others
Notes
As an example, consider the conflict over the Brent Spar oil rig that the owners, Royal Dutch Shell and Exxon, wanted to sink in the Atlantic Ocean. Following a worldwide campaign organized by the environmental group Greenpeace, they abandoned this plan. While there were publicly accessible estimations of the cost of the on-shore dismantling of Brent Spar, there was very little public information about the value Greenpeace placed on the prevention of the deep sea disposal.
Morath (2012) studies information acquisition in the framework of a war of attrition with a finite time horizon and shows that, even if information is available without cost, in equilibrium only one player may acquire information.
Note that the investment does not change the distribution of one’s value, nor one’s ability to compete in the contest. Investments in one’s value or ability have been studied by Münster (2007).
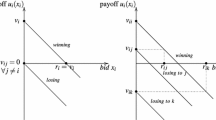
The analysis goes through for all \(v_{1}>0\). For \(v_{1}=0\), there is no equilibrium because player 1 will bid zero and player 2 has no best response since any strictly positive bid, however small, guarantees victory. This problem disappears if ties are broken in favor of the player with the higher valuation.
One interesting implication of (12) is that the bid of player \(2\) sometimes increases in the value of his opponent. To see this, suppose that \(\alpha _{2}=0.\) Then \(\beta _{2}\left( v_{2}\right) =F\left( v_{2}\right) v_{1}\) is increasing in \(v_{1}\). For the comparative statics, it must be kept in mind, however, that when \(v_{1}\) increases, this may increase \(\alpha _{2}\) by (9). It can be shown that, for this reason, \(\beta _{2}\) also sometimes decreases in \(v_{1}\).
If the left-hand side of (8) is exactly one, then no player has a mass point at zero.
If \(F\) is a uniform distribution on the unit interval, the left-hand side of (8) is infinite for any \(v_{1}>0\), thus (8) holds, and player \(2\) has a mass point at zero. We point out, however, that for a uniform distribution over an interval [a, b] with \(a>0,\) it depends on \(v_{1}\) whether player \(1\) or player \(2\) has a mass point at zero. In contrast, the argument in (13) does not hinge on the assumption that the lower bound of the support of \(F\) is zero.
This follows from Jensen’s inequality and the fact that \(1/V_{2}\) is a convex function of \(V_{2},\) together with assumption that \(E\left( V_{1}\right) =E\left( V_{2}\right) \) (see (13)).
Note that players have no private information when they decide whether to acquire information. Any reasonable belief about the opponent’s type is simply the prior distribution \(F\). Moreover, any continuation game has a unique Bayesian equilibrium. Therefore, we study the 2-by-2 game defined by the payoffs described in Facts 1–2 and Eqs. (16)–(17). This amounts to studying the perfect Bayesian equilibria of the game defined in Sect. 2.
Recall that, if exactly one player acquires information, v is defined as the highest type of the informed player that bids zero.
This is standard in the rent-seeking literature, see for example Baye et al. (1996).
For example, for \(F(v) =v\), \({\underline{\mathrm{c}}}<c^{\prime \prime }<\bar{c}\), and for \(F\left( v\right) =v^{3},\) we have \(c^{\prime \prime }<\) c \(\,<\bar{c }\).
In the symmetric equilibrium with randomization of information acquisition, under some parameter constellations, it may happen that ex post no player invests although in the first best one player should invest. To be more precise, if \(c^{\prime \prime }\le {\underline{\mathrm{c}}}\), then the number of players acquiring information is always weakly higher than in the first best. On the other hand, if \(c^{\prime \prime }>{\underline{\mathrm{c}}}\), then for any \(c\in \left( bad hbox,c^{\prime \prime }\right) ,\) in the first best exactly one player acquires information, whereas in the mixed equilibrium the number of players acquiring information is zero, one, or two, depending on the realizations of players’ randomization.
Our results can be used to investigate the overall welfare effects of policies such as subsidies or taxes on information acquisition. This requires careful thought, however. Such policies do not only affect the information acquisition itself, but also the interaction in the ensuing contest and thus the efficiency of the allocation and the expected bids. Hence, enforcing first best information acquisition does not necessarily maximize welfare. For example, suppose that \(\kappa =0\) and compare the case where no player acquires information to the case where one player acquires information. In equilibrium, the gain in allocative efficiency that results from information acquisition is lower than in the first best due to the mixed strategy equilibrium where low types of the informed player sometimes win and high types sometimes lose. Taking this into account means that the range of cost of information where no player should acquire information would be bigger than \(\left( c^{\prime \prime },\infty \right) \).
If \(i=2,\) this argument assumes \(v_{2}>0.\) But this is inconsequential since type \(v_{2}=0\) has zero probability.
If type \(v_{2}^{\prime }\) bids \(x_{l}\) with strictly positive probability, type \(v_{2}^{\prime }\) gains from shifting this probability mass to \(x.\) If type \(v_{2}^{\prime }\) bids \(x_{l}\) with probability zero, then, for any \(\varepsilon >0,\) the interval \(\left( x_{l},x_{l}+\varepsilon \right) \) has positive probability. Suppose that \(x_{l}>0.\) Then \(B_{1}\) is continuous on \(\left[ x_{l},x_{l}+\varepsilon \right] \) by Lemma 1. Therefore, if (18) does not hold, then for small enough \( \varepsilon >0,\, B_{1}\left( z\right) v_{2}^{\prime }-z<B_{1}\left( x\right) v_{2}^{\prime }-x\) for all \(z\in \left( x_{l},x_{l}+\varepsilon \right) \), and shifting probability mass from the interval \(\left( x_{l},x_{l}+\varepsilon \right) \) to \(x\) is beneficial. It remains to consider the case \(x_{l}=0.\) Then, \(B_{1}\) may have a discontinuity at \( x_{l}. \) However, \(B_{1}\) is right-continuous. Therefore, if (18) does not hold at \(x_{l}=0\), then for small enough \(\varepsilon >0,\, B_{1}\left( z\right) v_{2}^{\prime }-z<B_{1}\left( x\right) v_{2}^{\prime }-x \) for all \(z\in \left( 0,\varepsilon \right) \), and shifting probability mass from the interval \(\left( 0,\varepsilon \right) \) to \(x\) is beneficial.
References
Alcalde, J., Dahm, M.: Rent seeking and rent dissipation: a neutrality result. J. Public Econ. 94, 1–7 (2010)
Amann, E., Leininger, W.: Asymmetric all-pay auctions with incomplete information: the two-player case. Games Econ. Behav. 14, 1–18 (1996)
Barut, Y., Kovenock, D.: The symmetric multiple prize all-pay auction with complete information. Eur. J. Political Econ. 14, 627–644 (1998)
Baye, M.R., Kovenock, D., de Vries, C.G.: Rigging the lobbying process: an application of the all-pay auction. Am. Econ. Rev. 83, 289–294 (1993)
Baye, M.R., Kovenock, D., de Vries, C.G.: The all-pay auction with complete information. Econ. Theory 8, 362–380 (1996)
Baye, M.R., Kovenock, D., de Vries, C.G.: Contests with rank-order spillovers. Econ. Theory (2012). doi:10.1007/s00199-009-0489-2
Che, Y.-K., Gale, I.L.: Caps on political lobbying. Am. Econ. Rev. 88, 643–651 (1998)
Che, Y.-K., Gale, I.: Difference-form contests and the robustness of all-pay auctions. Games Econ. Behav. 30, 22–43 (2000)
Clark, D.J., Riis, C.: Competition over more than one prize. Am. Econ. Rev. 88, 276–289 (1998)
Dasgupta, P.: The theory of technological competition. In: Stiglitz, J.E., Mathewson, G.F. (eds.) New Developments in the Analysis of Market Structure, pp. 519–547. MIT Press, Cambridge (1986)
Ellingsen, T.: Strategic buyers and the social cost of monopoly. Am. Econ. Rev. 81, 648–657 (1991)
Engelbrecht-Wiggans, R., Milgrom, P., Weber, R.: Competitive bidding with proprietary information. J. Math. Econ. 11, 161–169 (1983)
Groh, C., Moldovanu, B., Sela, A., Sunde, U.: Optimal seedings in elimination tournaments. Econ. Theory 49, 59–80 (2012)
Hendricks, K., Porter, R.H.: An empirical study of an auction with asymmetric information. Am. Econ. Rev. 78, 865–883 (1988)
Hernando-Veciana, A.: Information acquisition in auctions: sealed bids vs. open bids. Games Econ. Behav. 65, 372–405 (2009)
Hillman, A.L., Riley, J.G.: Politically contestable rents and transfers. Econ. Politics 1, 17–40 (1989)
Hurley, T.M., Shogren, J.F.: Effort levels in a Cournot Nash contest with asymmetric information. J. Public Econ. 69(2), 195–210 (1998a)
Hurley, T.M., Shogren, J.F.: Asymmetric information in contests. Eur. J. Political Econ. 14, 645–665 (1998b)
Kim, J.: The value of an informed bidder in common value auctions. J. Econ. Theory 143, 585–595 (2008)
Konrad, K.A.: Strategy and Dynamics in Contests. Oxford University Press, Oxford (2009)
Krishna, V.: Auction Theory. Academic Press, San Diego (2002)
Krishna, V., Morgan, J.: An analysis of the war of attrition and the all-pay auction. J. Econ. Theory 72, 343–362 (1997)
Moldovanu, B., Sela, A.: The optimal allocation of prizes in contests. Am. Econ. Rev. 91(3), 542–558 (2001)
Morath, F., Münster, J.: Private versus complete information in auctions. Econ. Lett. 101, 214–216 (2008)
Morath, F.: Volunteering and the value of ignorance. Soc. Choice Welfare (2012). doi:10.1007/s00355-012-0679-x
Münster, J.: Contests with investment. Manag. Decis. Econ. 28(8), 849–862 (2007)
Persico, N.: Information acquisition in auctions. Econometrica 68, 135–148 (2000)
Polborn, M.: Investment under uncertainty in dynamic conflicts. Rev. Econ. Stud. 73, 505–529 (2006)
Roberson, B., Kvasov, D.: The non-constant-sum Colonel Blotto game. Econ. Theory (2012). doi:10.1007/s00199-011-0673-z
Sela, A.: Sequential two-prize contests. Econ. Theory (2012). doi:10.1007/s00199-010-0547-9
Skaperdas, S.: Contest success functions. Econ. Theory 7, 283–290 (1996)
Wärneryd, K.: Information in conflicts. J. Econ. Theory 110, 121–136 (2003)
Weber, R.: Auctions and competitive bidding. Proc. Symp. Appl. Math. 33, 143–170 (1985)
Author information
Authors and Affiliations
Corresponding author
Additional information
We would like to thank Michael R. Baye, Olivier Bos, Dan Kovenock, Wolfgang Leininger, Kai A. Konrad, Matthias Kräkel, Aner Sela, two anonymous referees, and participants of the Conference on “Contests: Theory and Applications” at the Stockholm School of Economics 2008. Financial support from the Deutsche Forschungsgemeinschaft through SFB/TR 15 is gratefully acknowledged.
A Appendix
A Appendix
1.1 A.1 Proof of Lemma 1
-
(i)
(Continuity) Suppose that \(B_{j}\) exhibits a discontinuity at some \(\tilde{x}>0\). This implies that a bid of \(x_{j}=\tilde{x}\) has strictly positive probability. Thus, there exist \(\varepsilon ,\varepsilon ^{\prime }>0\) such that player \(i\) strictly prefers \(x_{i}=\tilde{x} +\varepsilon \) over all \(x_{i}\in \left( \tilde{x}-\varepsilon ^{\prime }, \tilde{x}\right)\): shifting probability mass from \(\left( \tilde{x} -\varepsilon ^{\prime },\tilde{x}\right) \) to \(\tilde{x}+\varepsilon \) only involves an infinitesimally larger cost of effort, but strictly increases the probability of winning.Footnote 17 Since player \(i\) will not bid in \( \left( \tilde{x}-\varepsilon ^{\prime },\tilde{x}\right) \), player \(j\) can strictly increase his payoff by bidding \(\tilde{x}-\frac{\varepsilon ^{\prime }}{2}\) instead of \(\tilde{x}\).
-
(ii)
(Support) Let \(\bar{b}_{i}\) (b \(_{i}\)) denote the maximum (minimum) of the support of \(B_{i}\). Suppose that \(\bar{b}_{i}>\bar{b}_{j}\). Then, \(B_{j}\left( x\right) =1\) for all \(x\ge \bar{b}_{j}.\) Thus, player \(i\) prefers to bid \(x_{i}=\left( x_{i}^{\prime }+\bar{b}_{j}\right) /2\) to any bid \(x_{i}^{\prime }>\bar{b}_{j},\) contradicting \(\bar{b}_{i}>\bar{b}_{j}\). Hence, \(\bar{b}_{1}=\bar{b}_{2}=\bar{b}\). Since player 1 can ensure a payoff of zero by bidding zero, we must have \(\bar{b}\le v_{1}.\) Suppose that b \(_{i}>\) b \(_{j}\!>\!0.\) Then, any bid \(x_{j}<\) b \(_{i}\) loses with probability one; player \(j\) could increase his payoff by bidding zero instead, which is a contradiction. Now suppose b \(_{i}>\) b \(_{j}=0\). Then, player \(j\) strictly prefers a bid of zero over all bids in \(\left( \text{0},{\underline{\mathrm{b}}}_{i}\right) ,\) thus \(B_{j}\) has no probability mass in \(\left( \text{0},{\underline{\mathrm{b}}} _{i}\right) \). Since \(B_{j}\) has no mass points (except possibly at zero), it follows that \(B_{j}\) is constant on \(\left( 0,{\underline{\mathrm{b}}}_{i}\right] .\) But then there exists \(\varepsilon >0\) such that player \(i\) strictly prefers a bid of \(\varepsilon \) over any bid in \(\left[ {\underline{\mathrm{b}}}_{i},{\underline{\mathrm{b}}} _{i}+\varepsilon \right) \): a bid of \(\varepsilon \) has strictly lower costs but only a marginally lower probability of winning. This is a contradiction to the definition of b \(_{i}.\) Finally, suppose \({\underline{\mathrm{b}}}_{1}={\underline{\mathrm{b}}}_{2}={\underline{\mathrm{b}}}>0\). By (i), \(B_{j}\left( {\underline{\mathrm{b}}}\right) =0\), and there exists an \(\varepsilon >0\) such that \( x_{i}=0\) is preferred to any bid \(x_{i}\in \left[ {\underline{\mathrm{b}}},\ {\underline{\mathrm{b}}} +\varepsilon \right) ,\) which contradicts b \(_{i}>0\). Combining these arguments shows that \({\underline{\mathrm{b}}}_{1}={\underline{\mathrm{b}}}_{2}=0\).
-
(iii)
(Mass points at zero) If \(B_{j}\left( 0\right) >0\), there exists an \(\varepsilon >0\) such that player \(i\) prefers \(x_{i}=\varepsilon \) to \(x_{i}=0\). Hence, \(B_{i}\left(0\right) =0\). This shows that the bid distribution of at most one player can have a mass point at zero.
-
(iv)
(Monotonicity) Suppose that \(B_{j}\) is constant in an interval \(\left( x^{\prime },x^{\prime \prime }\right) \) where \(0\le x^{\prime }<x^{\prime \prime }\le \bar{b}\), further suppose that \(x^{\prime \prime }=\max \left\{ x\left|B_{j}\left( x\right) =B_{j}\left( x^{\prime }\right) \right. \right\} .\) Then \(B_{j}\left( x^{\prime }\right) =B_{j}\left( x^{\prime \prime }\right) <1\) since \(x^{\prime }<\bar{b}\). There exists an \(\varepsilon >0\) such that player \(i\) prefers \( x_{i}=x^{\prime }\) to all \(x_{i}\in \left( x^{\prime },x^{\prime \prime }+\varepsilon \right) :\) by bidding \(x^{\prime }\) player \(i\) reduces his probability of winning only by (at most) an infinitesimally small amount, but strictly decreases his expected cost of effort. Thus \(i\) does not bid in \(\left( x^{\prime },x^{\prime \prime }+\varepsilon \right) .\) Since \(B_{i}\) has no mass points, we have \(B_{i}\left( x^{\prime }\right) =B_{i}\left( x^{\prime \prime }+\varepsilon \right) .\) But then \(j\) prefers bidding \( x^{\prime }\) over any bid in \(\left[ x^{\prime \prime },x^{\prime \prime }+\varepsilon \right]\), and thus, we must have \(B_{j}\left( x^{\prime \prime }+\varepsilon \right) =B_{j}\left( x^{\prime }\right) ,\) contradicting \( x^{\prime \prime }=\max \left\{ x\left|B_{j}\left( x\right) =B_{j}\left( x^{\prime }\right) \right. \right\} .\)
1.2 A.2 Proof of Lemma 2
First, we show that no type of player \(2\) randomizes. Suppose to the contrary that some type \(v_{2}^{\prime }\) of player \(2\) does randomize. Let \(x_{l}\) ( \(x_{h}\)) be the infimum (supremum) of the support of the distribution of bids made by type \(v_{2}^{\prime }\). For any \(x>\) \(x_{l},\)
for otherwise \(v_{2}^{\prime }\) could gain from shifting probability mass to \(x\).Footnote 18 From (18),
Since \(B_{1}\) is strictly increasing, for any \(v_{2}^{\prime \prime }<v_{2}^{\prime }\) we have
or
that is, type \(v_{2}^{\prime \prime }\) strictly prefers to bid \(x_{l}\) over bidding \(x.\) Therefore, for all \(v_{2}^{\prime \prime }<v_{2}^{\prime }\), the supremum of the support of the distribution of bids made by type \(v_{2}^{\prime \prime }\) must be weakly smaller than \(x_{l}\). Similarly, for all \(v_{2}^{\prime \prime \prime }>v_{2}^{\prime }\), the infimum of the support of the distribution of bids made by type \( v_{2}^{\prime \prime \prime }\) must be weakly higher than \(x_{h}.\) Therefore, only type \(v_{2}^{\prime }\) bids in \(\left( \,x_{l},\,x_{h}\right) .\) Since the distribution of types, \(F,\) is continuous, it follows that \( B_{2}\) is constant on \(\left( \,x_{l},\,x_{h}\right) ,\) contradicting Lemma 1.
It follows that player \(2\) plays a pure strategy \(\beta _{2}:\left[ 0,1 \right] \rightarrow \left[ 0,\infty \right) \). Moreover, \(\beta _{2}\) is weakly increasing. Now suppose that \(v_{2}^{\prime }<v_{2}^{\prime \prime }\) and \(\beta _{2}\left( v_{2}^{\prime }\right) =\beta _{2}\left( v_{2}^{\prime \prime }\right) \). Since \(\beta _{2}\) is weakly increasing, it follows that \( \beta _{2}\left( v_{2}\right) =\beta _{2}\left( v_{2}^{\prime }\right) \) for all \(v_{2}\in \left[ v_{2}^{\prime },v_{2}^{\prime \prime }\right] \). Therefore, \(B_{2}\) has an atom at \(\beta _{2}\left( v_{2}^{\prime }\right) \) (the size of the atom is at least \(F\left( v_{2}^{\prime \prime }\right) -F\left( v_{2}^{\prime }\right) \)). Since \(B_{2}\) is continuous except possibly at zero, this atom can only be at \(\beta _{2}\left( v_{2}^{\prime }\right) =0\).
This shows that there is a v \(\in \left[ 0,1\right) \) such that, first, for all \(v_{2}\le \) v, \(\beta _{2}\left( v_{2}\right) =0,\) and second, \( \beta _{2}\) is strictly increasing on \(\left[ {\underline{\mathrm{v}}},1\right] .\) Since \(B_{2}\) is strictly increasing, \(\beta _{2}\) has to be continuous as well.
1.3 A.3. Proof of Lemma 3
We first show that \(B_{1}\) is differentiable at any \(x_{2}\in \left( 0,\bar{b }\right) .\) Let \(v_{2}=\beta _{2}^{-1}\left( x_{2}\right) \) and consider a strictly increasing sequence \(v_{2}^{n}\) with \(v_{2}^{n}\in \left( bad hbox,1\right) \) and \(\lim _{n\rightarrow \infty }v_{2}^{n}=v_{2}\). For notational brevity let \(x_{2}^{n}=\beta _{2}\left( v_{2}^{n}\right) .\) Then, \(x_{2}^{n}\) is strictly increasing and \(\lim _{n\rightarrow \infty }x_{2}^{n}=x_{2}.\)
Bidding \(x_{2}^{n}\) is at least as good as bidding \(x_{2}\) for type \( v_{2}^{n},\) thus
or
Taking \(\lim \sup \), we get
Similarly, for type \(v_{2},\) bidding \(x_{2}\) is at least as good as bidding \( x_{2}^{n}.\) Thus,
Rearranging and taking \(\lim \inf ,\) we get
From (20) and (19), it follows that
A parallel argument, which considers a strictly decreasing sequence \( v_{2}^{n} \) with limit \(v_{2},\) shows that
Thus, \(B_{1}\) is differentiable at \(v_{2}\), with
We next show that the bid distribution \(B_{2}\) is differentiable. Since \( B_{1}\) is strictly increasing on \(\left( 0,\bar{b}\right) \), player \(1\) must be indifferent between all bids \(x\in \left( 0,\bar{b}\right) .\) Fix one \( x_{1}\in \left( 0,\bar{b}\right) .\) Consider a sequence \(x_{1}^{n}\) with limit \(x_{1}\) and with \(x_{1}^{n}\in \left( 0,\bar{b}\right) \) for all \(n.\) For all \(n,\) player \(1\) is indifferent between bidding \(x_{1}^{n}\) and bidding \(x_{1}:\)
Rearranging,
Thus,
and therefore \(B_{2}\) is differentiable.
Since \(F\) is differentiable by assumption, it follows that \(\beta _{2}\) must be differentiable as well.
1.4 A.4. Proof of Lemma 4
(i) Suppose to the contrary that \(\alpha _{1}>0.\) Then \(\alpha _{2}=0\) by (6) and thus
contradiction. Thus, \(\alpha _{1}=0.\) Inserting \(\alpha _{1}=0\) in (7), we get (9). The left-hand side of (9) is strictly greater than one for \(\alpha _{2}=0,\) it strictly decreases in \(\alpha _{2},\) and is equal to zero for \(\alpha _{2}=1.\) By continuity, there is a unique \(\alpha _{2}\in \left( 0,1\right) \) such that (9) holds. Part (ii) can be proven similarly. From (i) and (ii), it follows that \(\alpha _{1}\) and \(\alpha _{2}\) are uniquely determined.
1.5 A.5. Proof of Proposition 1
Uniqueness follows from the discussion in the main text. It remains to establish that the strategies are an equilibrium. Consider player \(1\) and suppose player \(2\) follows (12). The expected payoff of player \(1\) for a bid \(x_{1}\in \left( 0,\left( 1-\alpha _{2}\right) v_{1} \right] \) is equal to
since \(\beta _{2}^{-1}\) exists on \(\left( 0,\left( 1-\alpha _{2}\right) v_{1} \right] \). Inserting (12), we get \(E\left[ u_{1}\left( x_{1}\right) \right] =\alpha _{2}v_{1}\) for all \(x_{1}\in \left( 0,\left( 1-\alpha _{2}\right) v_{1}\right] .\) Moreover, if (8) does not hold, then \(\alpha _{2}=0\) and player \(1\) has a payoff of zero; thus, in this case he is indifferent between all \(x_{1}\in \left[ 0,\left( 1-\alpha _{2}\right) v_{1}\right] .\) Bidding more than \(\left( 1-\alpha _{2}\right) v_{1}\) is always suboptimal. Thus (11) is a best response.
Now consider player \(2\) and suppose he has a valuation \(v_{2}.\) Given \( B_{1}, \) his payoff \(B_{1}\left( x\right) v_{2}-x\) is strictly concave in his bid \(x \) since
If \(v_{2}>F^{-1}\left( \alpha _{2}\right) \), then the first-order condition (3) describes the unique maximum. If \(v_{2}\le F^{-1}\left( \alpha _{2}\right) ,\) then for all \(x_{2}>0,\)
Therefore, (12) is a best response.
1.6 A.6. Proof of Proposition 2
Suppose player \(j\) does not acquire information. If \(i\) does not acquire information either, he gets an expected payoff of zero by Fact 1; if \(i\) acquires information, his payoff is described by (17). Hence, \(i\)’s best response is to acquire information if and only if \(c\) is smaller than
where, from (15), v \(=F^{-1}\left( \alpha _{i}\right) >0\), and v is defined by
Note that from (22), it follows that v \(<E\left( V\right) \).
Now suppose that \(j\) acquires information. If \(i\) remains uninformed, he gets \(F\left({\underline{\mathrm{v}}}\right) E\left( V\right) \), as in (16). If \(i\) acquires information, his payoff is described by (14). Thus, \(i\)’s best response is to acquire information if and only if \(c\) is smaller than
where again v is defined by (22).
Let
(In Appendix A.7, we will show that in the first best, both players acquire information if and only if \(c<c^{\prime }.\)) The following lemmas will be used repeatedly below.
Lemma 5
Proof
For the equality,
The inequality \(c^{\prime }>0\) follows from Jensen’s inequality. To see this, define
Since \(g\) is strictly convex in \(v_{i}\),
or equivalently
\(\square \)
Lemma 6
(i) c \(>c^{\prime }\) and (ii) \(\bar{c}>\) c.
Proof
(i) Using Lemma 5,
Adding and subtracting both \(\int _{0}^{E\left( V\right) }{\underline{\mathrm{v}}} \text{ d}F\left( v_{j}\right) \) and \(\int _{{\underline{\mathrm{v}}}}^{E\left( V\right) }{\underline{\mathrm{v}}}\frac{E\left( V\right) }{v_{j}}\text{ d}F\left( v_{j}\right) \) yields
First observe that
where the second equality uses (22). Therefore,
which is strictly positive.
(ii) With (21) and (23), \(\bar{c}-\) c is equal to
where
if \(v_{i}\le \, \) v, and
if \(v_{i}>\) v. Then, it is sufficient to show that \(h\left( v_{i}\right) >0\) for all \(v_{i}\in \left[ 0,1\right] \).
- Case 1: :
-
\(v_{i}\le \) v \(.\) From (22), it follows that v \(<E\left( V\right) \), and thus
$$\begin{aligned} \int _{0}^{{\underline{\mathrm{v}}}}E\left( V\right) \text{ d}F\left( v_{j}\right) >\int _{0}^{v_{i}}v_{i}\text{ d}F\left( v_{j}\right) >\int _{0}^{v_{i}}\left( v_{i}-v_{j}\right) \text{ d}F\left( v_{j}\right) . \end{aligned}$$ - Case 2: :
-
\(v_{i}\in \left( {\underline{\mathrm{v}}},E\left( V\right) \right] .\) Here, \(h\left( v_{i}\right) \) is equal to
$$\begin{aligned} \int _{{\underline{\mathrm{v}}}}^{v_{i}}\frac{\left( v_{i}-v_{j}\right) \left( E\left( V\right) -v_{j}\right) }{v_{j}}\text{ d}F\left( v_{j}\right) +\int _{0}^{{\underline{\mathrm{v}}} }\left( E\left( V\right) -v_{i}+v_{j}\right) \text{ d}F\left( v_{j}\right) . \end{aligned}$$The first term is strictly positive because \(v_{j}\le v_{i}\le E\left( V\right) \) and \(v_{i}>\) v. The second term is strictly positive as \( v_{i}\le E\left( V\right) \) and, by (15), v \(>0\).
- Case 3: :
-
\(v_{i}\in \left( E\left( V\right) ,1\right] .\) Since v is independent of \(v_{i}\), we get
$$\begin{aligned} h^{\prime }\left( v_{i}\right)&= \int _{{\underline{\mathrm{v}}}}^{v_{i}}\frac{E\left( V\right) }{v_{j}}\text{ d}F\left( v_{j}\right) -\int _{0}^{v_{i}}\text{ d}F\left( v_{j}\right) , \\ h^{\prime \prime }\left( v_{i}\right)&= \frac{E\left( V\right) }{v_{i}} F^{\prime }\left( v_{i}\right) -F^{\prime }\left( v_{i}\right) , \end{aligned}$$hence, \(h\) is strictly concave for \(v_{i}>E\left( V\right) \). Moreover, as \( v_{i}\rightarrow 1\), \(h^{\prime }\) converges to
$$\begin{aligned} \int _{{\underline{\mathrm{v}}}}^{1}\frac{E\left( V\right) }{v_{j}}\text{ d}F\left( v_{j}\right) -\int _{0}^{1}\text{ d}F\left( v_{j}\right) =1-1=0. \end{aligned}$$(The first integral is one by (22).) Thus, \( h^{\prime }\) must be positive for all \(v_{i}\in \left( E\left( V\right) ,1\right) \) and thus \(h\left( v_{i}\right) >h\left( E\left( V\right) \right) >0\) where the last inequality follows from case 2.\(\square \)
We are now in a position to prove Proposition 2. From Lemmas 5 and , it follows directly that \(\bar{c}>\) c \(>0\). Thus, (i) if \(c<\) c, information acquisition is strictly dominant. (ii) If c \( <c<\bar{c}\), a player invests in information only if the opponent remains uninformed, and there exist two asymmetric equilibria where exactly one player invests. Moreover, there is a symmetric equilibrium where both players invest in information with probability \(p=\left( \bar{c}-c\right) /\left( \bar{c}- {\underline{\mathrm{c}}}\right) :\) if player \(i\) acquires information, he gets
which is equal to his payoff if he remains uninformed. Thus, \(i\) is indifferent between investing and not investing in information. Moreover, for all \(p\) that are strictly smaller (greater) than this critical value, \(i\) strictly prefers (not) to acquire information. Finally, (iii) if \(c>\bar{c}\) , not investing is strictly dominant.
1.7 A.7. Proof of Proposition 3
If the social planner does not acquire information, welfare equals \(E\left( V\right) \). If she acquires information about the valuation of one player, welfare is equal to
If the social planner acquires information about both players, welfare equals
As above, let
Moreover, let
Lemma 7
(i) \(0<c^{\prime }<c^{\prime \prime }\) and (ii) \(c^{\prime }<\) c and \( c^{\prime \prime }<\bar{c}.\)
Proof
(i) In Lemma 5, we have already shown that \(c^{\prime }>0\). Moreover, using Lemma ,
which is strictly smaller than
(ii) The first inequality is Lemma , part (i). Moreover, by (21) and (25), \(\bar{c}>c^{\prime \prime }\) is equivalent to
By (17), the left-hand side is \(i\)’s ex ante expected payoff if \(i\) acquired information and \(j\) remained uninformed. Since, in this case, \(j\) never bids higher than his expected value, the LHS must be weakly higher than the RHS, because the latter is the payoff \(i\) could ensure by bidding \(E\left( V\right) \) for all types \(v_{i}\ge E\left( V\right) \) and bidding zero otherwise. It remains to show that for some realizations of \(v_{i}\), \(i\) can do strictly better. Note first that \( F^{-1}\left( \alpha _{i}\right) = {\underline{\mathrm{v}}}>0\), that is, \(j\)’s maximum bid is \(\bar{ b}=\left( 1-\alpha _{i}\right) E\left( V\right) <E\left( V\right) \). Hence, for all realizations \(v_{i}\in \left( \left( 1-\alpha _{i}\right) E\left( V\right) ,E\left( V\right) \right) \), \(i\) can ensure a strictly positive payoff by bidding \(\left( 1-\alpha _{i}\right) E\left( V\right) \), and hence, the LHS must be strictly larger than the RHS. \(\square \)
The inequalities in (i) allow us to characterize first best information acquisition: if \(c<c^{\prime }\), both should acquire information; if \(c\in \left( c^{\prime },c^{\prime \prime }\right) ,\) exactly one player should acquire information; finally, if \(c>c^{\prime \prime },\) no one should. With (ii), we can compare equilibrium investments and first best investments (see Fig. 2 in the main text). If \(c<c^{\prime },\) both players invest as in the first best. If \(c\in \left( c^{\prime },\min \left\{ {\underline{\mathrm{c}}} ,c^{\prime \prime }\right\} \right) ,\) both players acquire information although exactly one player should. If \(c\in \left( \min \left\{ {\underline{\mathrm{c}}},c^{\prime \prime }\right\} ,c^{\prime \prime }\right) ,\) in the asymmetric equilibria exactly one player acquires information, as in the first best. If \(c\in \left( c^{\prime \prime },\bar{c}\right) ,\) at least one player acquires information, but neither of the players should. Finally, if \(c>\bar{c},\) no player invests, as in the first best. Therefore, the number of players investing in information is higher than the first best.
1.8 A.8. Proof of Proposition 4
If no player invests in information, both get an expected payoff of zero. If only player \(i\) invests, \(i\)’s expected payoff is \(E_{v_{i}}\left[ \max \left\{ v_{i}-E\left( V\right) ,0\right\} \right] -c\), while \(j\) gets \( E_{v_{i}}\left[ \max \left\{ E\left( V\right) -v_{i},0\right\} \right] \). If both players acquire information, each of them gets \(E_{v_{i},v_{j}}\left[ \max \left\{ v_{i}-v_{j},0\right\} \right] -c\).
Now suppose that \(j\) remains uninformed. Player \(i\)’s best response is to acquire information whenever \(c\) is smaller than \(E_{v_{i}}\left[ \max \left\{ v_{i}-E\left( V\right) ,0\right\} \right] \) which, with (25), is equal to \(c^{\prime \prime }\). If \(j\) acquires information, \(i\) invests whenever \(c\) is smaller than
which, by Lemma 5, is equal to \(c^{\prime }\). Since \(0<c^{\prime }<c^{\prime \prime }\), both players (no player) acquire information if \(c<c^{\prime }\) (\(c>c^{\prime \prime }\)). If \(c\in \left(c^{\prime },c^{\prime \prime }\right) \), there are two equilibria where exactly one player acquires information, and a mixed strategy equilibrium where players acquire information with probability \(\left( c^{\prime \prime }-c\right) /\left( c^{\prime \prime }-c^{\prime }\right) \).
1.9 A.9. Proof of Proposition 5
-
(i)
We first analyze whether there can be an equilibrium where both players acquire information with probability \(1\). If this is the case, then they bid as in Fact 2 and both get a payoff of
$$\begin{aligned} \int _{0}^{1}\int _{0}^{v_{i}}\left( v_{i}-v_{j}\right) \text{ d}F\left( v_{j}\right) \text{ d}F\left( v_{i}\right) -c. \end{aligned}$$Now suppose that \(i\) deviates and remains uninformed. Then, his optimal bid is as if he had a value of \(E\left( V\right) \) which leads to a deviation payoff of
$$\begin{aligned} \int _{0}^{E\left( V\right) }\left( E\left( V\right) -v_{j}\right) \text{ d}F\left( v_{j}\right) . \end{aligned}$$Hence, it pays off to save the cost of information whenever \(c\) is larger than
$$\begin{aligned} \int _{0}^{1}\int _{0}^{v_{i}}\left( v_{i}-v_{j}\right) \text{ d}F\left( v_{j}\right) \text{ d}F\left( v_{i}\right) -\int _{0}^{E\left( V\right) }\left( E\left( V\right) -v_{j}\right) \text{ d}F\left( v_{j}\right) \end{aligned}$$which, by Lemma 5, is equal to \(c^{\prime }\). Thus, if and only if \(c<c^{\prime }\), an equilibrium exists where both players acquire information.
-
(ii)
Now suppose that both players do not invest in information with probability \(1\). Then, both get zero payoff. If \(i\) deviates and acquires information, his optimal bid is zero if \(v_{i}\le E\left( V\right) \) and \( E\left( V\right) \) if \(v_{i}>E\left( V\right) \). (The type \(v_{i}=E\left( V\right) \) is exactly indifferent. Thus, lower types prefer a bid of zero, and higher types prefer a bid at the upper bound of the support of \(j\)’s bids.) The deviation payoff is
$$\begin{aligned} \int _{E\left( V\right) }^{1}\left( v_{i}-E\left( V\right) \right) \text{ d}F\left( v_{i}\right) -c. \end{aligned}$$Therefore, if and only if \(c\) is larger than \(c^{\prime \prime }\) (from (25)), there is an equilibrium where no player acquires information.
Rights and permissions
About this article
Cite this article
Morath, F., Münster, J. Information acquisition in conflicts. Econ Theory 54, 99–129 (2013). https://doi.org/10.1007/s00199-012-0710-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00199-012-0710-6